三角関数とグラフ
三角関数とグラフ
中央大2020微分 ３次関数と直線の交点
単元：
#数Ⅱ#三角関数#微分法と積分法#三角関数とグラフ#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(x)=x^3+3x^2-2$と$y=k(x-1)-2$が相異なる3点で交わる$k$の範囲を求めよ.
2020中央大(経)過去問
この動画を見る
$f(x)=x^3+3x^2-2$と$y=k(x-1)-2$が相異なる3点で交わる$k$の範囲を求めよ.
2020中央大(経)過去問
早稲田大2019微分・３次関数と直線の交点
単元：
#数Ⅱ#三角関数#微分法と積分法#三角関数とグラフ#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$y=x^2$上の$(a,a^2)$における接線が$y=x^3-ax$と3点で交わる$a$の範囲を求めよ.
2019早稲田大過去問
この動画を見る
$y=x^2$上の$(a,a^2)$における接線が$y=x^3-ax$と3点で交わる$a$の範囲を求めよ.
2019早稲田大過去問
早稲田（商）三角関数・微分
単元：
#数Ⅱ#三角関数#微分法と積分法#三角関数とグラフ#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(\sin\theta+\cos\theta)^6-6\sin\theta\cos\theta$の最大値・最小値を求めよ.
1996早稲田(商)過去問
この動画を見る
$(\sin\theta+\cos\theta)^6-6\sin\theta\cos\theta$の最大値・最小値を求めよ.
1996早稲田(商)過去問
20年5月数学検定1級1次試験（微分）
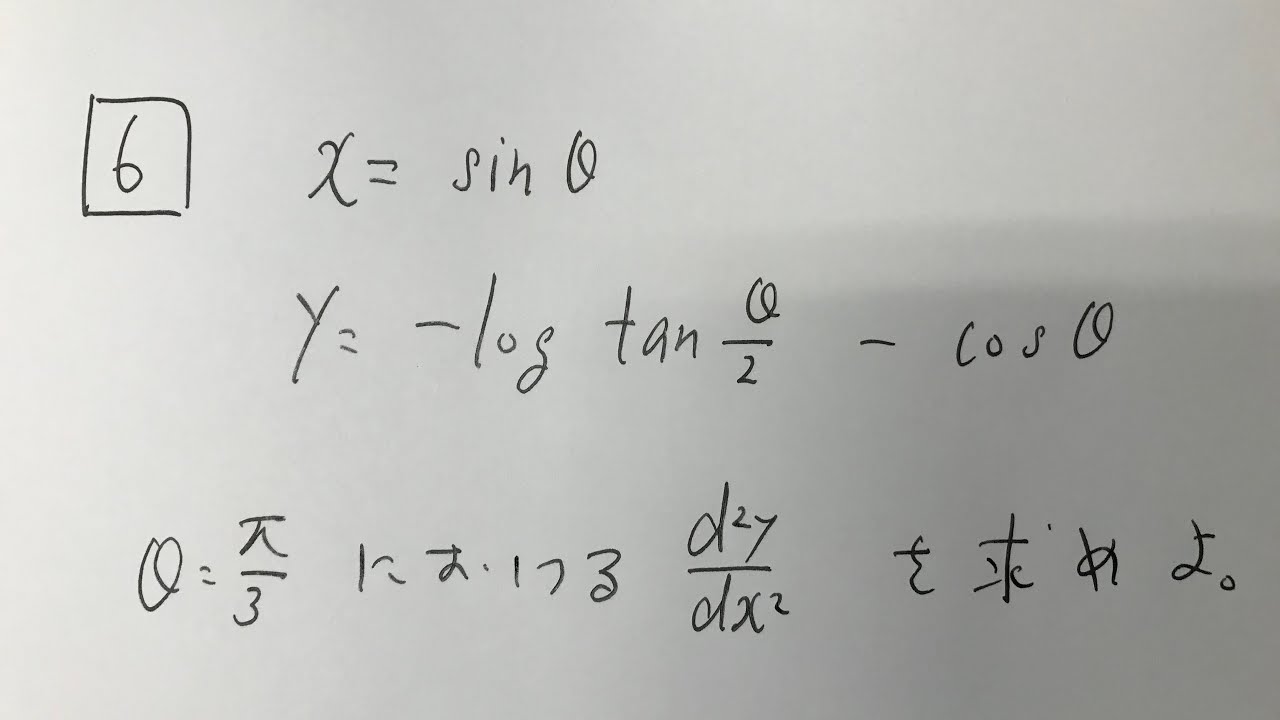
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
6⃣
x=sinθ
$y=-log tan \frac{θ}{2}-cosθ$
$θ=\frac{\pi}{3}$における$\frac{dy}{dx^2}$を求めよ。
この動画を見る
6⃣
x=sinθ
$y=-log tan \frac{θ}{2}-cosθ$
$θ=\frac{\pi}{3}$における$\frac{dy}{dx^2}$を求めよ。
20年5月数学検定1級1次試験（三角関数）
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
2⃣
$tan(2Arctan \frac{1}{3} + Arctan \frac{1}{12} )$
この動画を見る
2⃣
$tan(2Arctan \frac{1}{3} + Arctan \frac{1}{12} )$
３次関数 三角形の面積最大 お茶の水女子大
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比（内分・外分・二等分線）#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#お茶の水女子大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(x)=x^3-6x^2+8x$,3点$O,A(3,f(3))$,$P(t,f(t)),0\lt t\leqq 4,t\neq 3$である.
$\triangle OAP$の面積が最大となる$t$の値を求めよ.
1987お茶の水女子大過去問
この動画を見る
$f(x)=x^3-6x^2+8x$,3点$O,A(3,f(3))$,$P(t,f(t)),0\lt t\leqq 4,t\neq 3$である.
$\triangle OAP$の面積が最大となる$t$の値を求めよ.
1987お茶の水女子大過去問
20年5月数学検定準1級1次試験（三角関数）
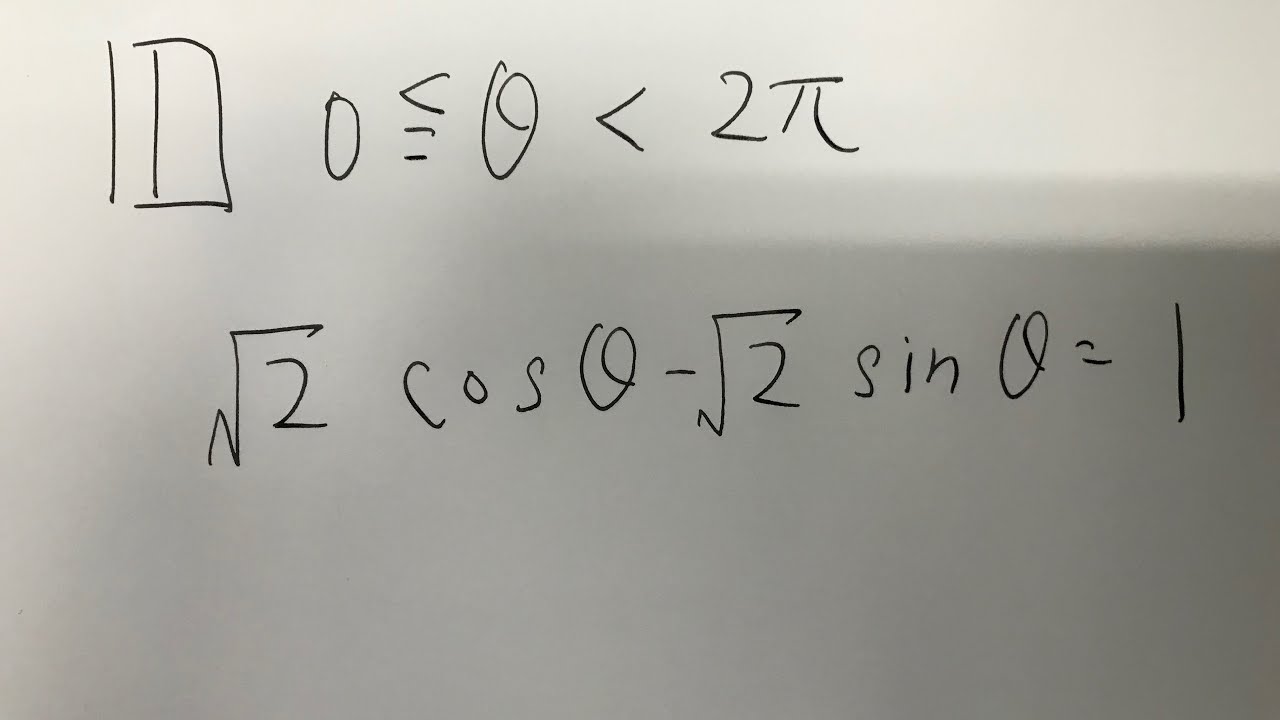
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
1⃣ $0 \leqq θ < 2\pi$
$\sqrt 2 cosθ - \sqrt 2 sinθ = 1$
この動画を見る
1⃣ $0 \leqq θ < 2\pi$
$\sqrt 2 cosθ - \sqrt 2 sinθ = 1$
18神奈川県採用試験（数学：複素数）
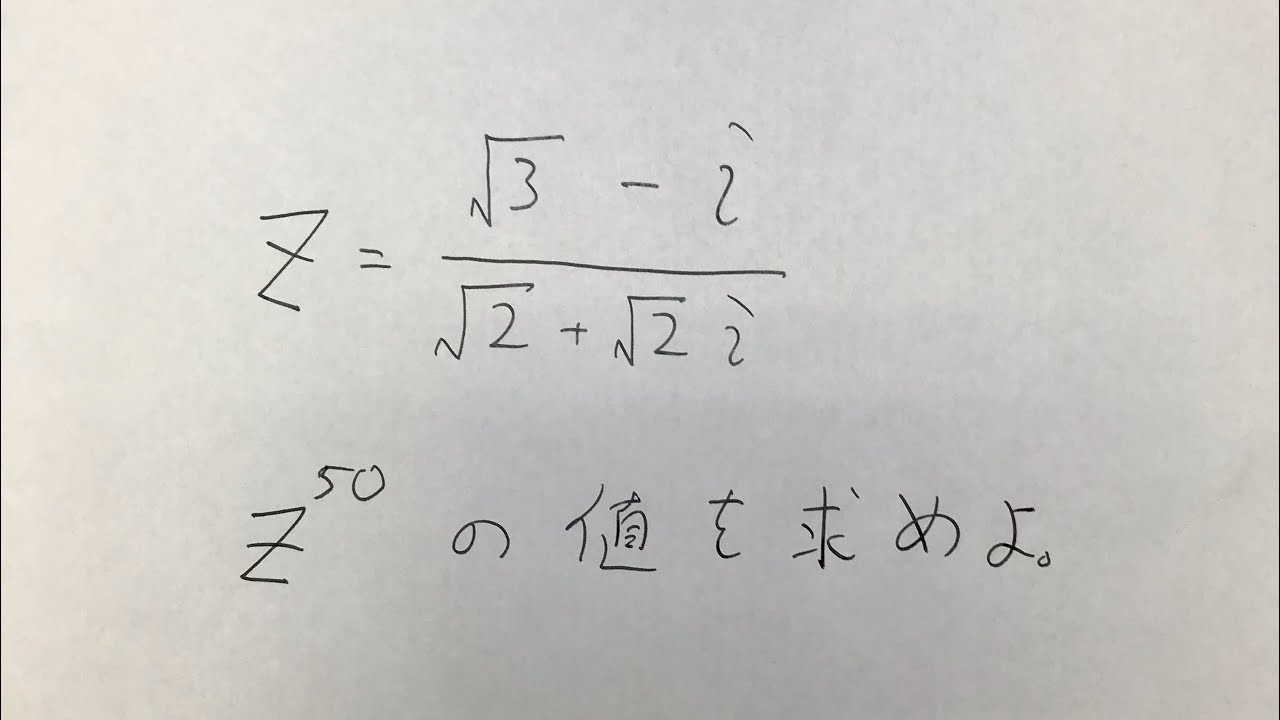
単元：
#数Ⅱ#複素数平面#三角関数#三角関数とグラフ#複素数平面#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$Z=\frac{\sqrt 3 - i}{\sqrt 2 + \sqrt 2 i } , Z^{50}$を求めよ。
この動画を見る
$Z=\frac{\sqrt 3 - i}{\sqrt 2 + \sqrt 2 i } , Z^{50}$を求めよ。
京都府採用試験数学【2016】
単元：
#数Ⅰ#数A#数Ⅱ#数と式#場合の数と確率#平面上のベクトル#複素数平面#図形と計量#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#集合と命題（集合・命題と条件・背理法）#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#整数の性質#場合の数#確率#約数・倍数・整数の割り算と余り・合同式#三角関数#指数関数と対数関数#三角関数とグラフ#指数関数#対数関数#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#微分とその応用#積分とその応用#複素数平面#微分法#色々な関数の導関数#関数の変化（グラフ・最大最小・方程式・不等式）#定積分#面積・体積・長さ・速度#数学(高校生)#数C#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
1. x+y+z=10の正の整数解の個数を求めよ。
2. 3つのサイコロを投げる。
出る目の最大値と最小値の差が2になる確率を求めよ。
3. 複素数$(\frac{-1+\sqrt{3}i}{2})^{2015} + (\frac{-1-\sqrt{3}i}{2})^{2015}$
4. $log_{2}3$は無理数を示せ
5. $△OAB = \frac{|a_1b_2-a_2b_1|}{2}$を示せ
＊図は動画内参照
6. f(x)=e^x sinx
(1) $0 \leqq x \leqq \pi$ y=f(x)の極大値を求めよ。
(2)x軸とy=f(x) ($0 \leqq x \leqq \pi$)で囲まれた面積を求めよ。
7. $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2015}{2015}$のうち既約分数の個数を求めよ。
8. $n \in \mathbb{ N }$
$2(\sqrt{n+1} - 1) < 1 + \frac{1}{\sqrt 2} + \frac{1}{\sqrt 3} + \cdots + \frac{1}{\sqrt n}$
この動画を見る
1. x+y+z=10の正の整数解の個数を求めよ。
2. 3つのサイコロを投げる。
出る目の最大値と最小値の差が2になる確率を求めよ。
3. 複素数$(\frac{-1+\sqrt{3}i}{2})^{2015} + (\frac{-1-\sqrt{3}i}{2})^{2015}$
4. $log_{2}3$は無理数を示せ
5. $△OAB = \frac{|a_1b_2-a_2b_1|}{2}$を示せ
＊図は動画内参照
6. f(x)=e^x sinx
(1) $0 \leqq x \leqq \pi$ y=f(x)の極大値を求めよ。
(2)x軸とy=f(x) ($0 \leqq x \leqq \pi$)で囲まれた面積を求めよ。
7. $\frac{1}{2015} , \frac{2}{2015} , \cdots , \frac{2015}{2015}$のうち既約分数の個数を求めよ。
8. $n \in \mathbb{ N }$
$2(\sqrt{n+1} - 1) < 1 + \frac{1}{\sqrt 2} + \frac{1}{\sqrt 3} + \cdots + \frac{1}{\sqrt n}$
三次関数の最大値 微分の基礎 大阪教育大
単元：
#数Ⅱ#三角関数#微分法と積分法#三角関数とグラフ#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(x)=-x^3-3x^2+3kx+3k+2$の$-1\leqq x\leqq 1$における最大値を求めよ.
2008大阪教育大過去問
この動画を見る
$f(x)=-x^3-3x^2+3kx+3k+2$の$-1\leqq x\leqq 1$における最大値を求めよ.
2008大阪教育大過去問
【高校数学】三角関数のグラフの裏技～これを覚えればグラフは余裕～【数学Ⅱ】
京都大 三角関数 4倍角の公式 最大値・最小値
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(\theta)=\cos4\theta-4\sin^2\theta$
$0 \leqq \theta \leqq \displaystyle \frac{3}{4}\pi$における$f(\theta)$の最大値・最小値を求めよ
出典：2004年京都大学 過去問
この動画を見る
$f(\theta)=\cos4\theta-4\sin^2\theta$
$0 \leqq \theta \leqq \displaystyle \frac{3}{4}\pi$における$f(\theta)$の最大値・最小値を求めよ
出典：2004年京都大学 過去問
青山学院大 三角方程式の解の個数
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\sin^2\theta-k\sin\theta+\displaystyle \frac{1}{4}=0$
$(0 \leqq \theta \lt \pi)$
解の個数を求めよ
出典：2009年青山学院大学 過去問
この動画を見る
$\sin^2\theta-k\sin\theta+\displaystyle \frac{1}{4}=0$
$(0 \leqq \theta \lt \pi)$
解の個数を求めよ
出典：2009年青山学院大学 過去問
東北大 三角方程式 Mathematics Japanese university entrance exam
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比（三角比・拡張・相互関係・単位円）#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$0 \leqq x \lt 2\pi$方程式を解け
（1）
$\sin^3x+\cos^3x=1$
（2）
$\sin^3x+\cos^3x+\sin x=2$
出典：2007年東北大学 過去問
この動画を見る
$0 \leqq x \lt 2\pi$方程式を解け
（1）
$\sin^3x+\cos^3x=1$
（2）
$\sin^3x+\cos^3x+\sin x=2$
出典：2007年東北大学 過去問
京都大 三角関数 ３次関数 解の個数 Mathematics Japanese university entrance exam
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#三角関数とグラフ#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$0 \leqq \theta \lt 2\pi$
$\cos 3\theta - \cos 2\theta+3\cos\theta-1=a$を満たす$\theta$の個数
出典：京都大学 過去問
この動画を見る
$0 \leqq \theta \lt 2\pi$
$\cos 3\theta - \cos 2\theta+3\cos\theta-1=a$を満たす$\theta$の個数
出典：京都大学 過去問
信州大(医）三角関数 最大値・最小値 Mathematics Japanese university entrance exam
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\sin^4x+2\sin x \cos x+\cos ^4x$の最小値と最大値を求めよ
出典：1986年信州大学医学部 過去問
この動画を見る
$\sin^4x+2\sin x \cos x+\cos ^4x$の最小値と最大値を求めよ
出典：1986年信州大学医学部 過去問
長崎大(医) 三角関数 方程式解の個数 Mathematics Japanese university entrance exam
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次関数とグラフ#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$0 \leqq x \leqq \pi$のとき、方程式$\cos 2x+4a \sin x +a-2=0$が異なる2つの解をもつための$a$の範囲
出典：1988年長崎大学医学部 過去問
この動画を見る
$0 \leqq x \leqq \pi$のとき、方程式$\cos 2x+4a \sin x +a-2=0$が異なる2つの解をもつための$a$の範囲
出典：1988年長崎大学医学部 過去問
信州大 三角関数・微分 Mathematics Japanese university entrance exam
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#三角関数とグラフ#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(x)=2\cos \displaystyle \frac{x}{2}+8 \cos \displaystyle \frac{x}{3}$のとりうる範囲は？
出典：2004年国立大学法人信州大学 過去問
この動画を見る
$f(x)=2\cos \displaystyle \frac{x}{2}+8 \cos \displaystyle \frac{x}{3}$のとりうる範囲は？
出典：2004年国立大学法人信州大学 過去問
東大 三角比 放物線 Mathematics Japanese university entrance exam Tokyo University
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#図形と計量#2次関数とグラフ#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$y=2 \sqrt{ 3 }(x- \cos \theta)^2+ \sin \theta$
$y=-2 \sqrt{ 3 }(x+ \cos \theta)^2- \sin \theta$
この2つの放物線が相違となる2点で交わるような$\theta$の範囲
出典：2002年東京大学 過去問
この動画を見る
$y=2 \sqrt{ 3 }(x- \cos \theta)^2+ \sin \theta$
$y=-2 \sqrt{ 3 }(x+ \cos \theta)^2- \sin \theta$
この2つの放物線が相違となる2点で交わるような$\theta$の範囲
出典：2002年東京大学 過去問
【高校数学】三角関数⑧～グラフで解く最大値・最小値～ 4-10【数学Ⅱ】
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
次の関数の最大値と最小値を求めよ。また、そのときのθの値を求めよ。
(1) y=sinθ-1(0≦θ≦$\displaystyle \frac{7π}{4}$)
(2) y=2cos(θ+$\displaystyle \frac{π}{3}$)(0≦θ≦π)
この動画を見る
次の関数の最大値と最小値を求めよ。また、そのときのθの値を求めよ。
(1) y=sinθ-1(0≦θ≦$\displaystyle \frac{7π}{4}$)
(2) y=2cos(θ+$\displaystyle \frac{π}{3}$)(0≦θ≦π)
【高校数学】三角関数⑥～三角方程式の応用～ 4-8【数学Ⅱ】
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
三角関数⑥
0≦θ<2πのとき、次の方程式を満たすθを求めよ。
(1) sin(θ-$\displaystyle \frac{π}{6}$)=-$\displaystyle \frac{1}{2}$
(2) cos(θ+$\displaystyle \frac{π}{4}$)=$\displaystyle \frac{√3}{2}$
この動画を見る
三角関数⑥
0≦θ<2πのとき、次の方程式を満たすθを求めよ。
(1) sin(θ-$\displaystyle \frac{π}{6}$)=-$\displaystyle \frac{1}{2}$
(2) cos(θ+$\displaystyle \frac{π}{4}$)=$\displaystyle \frac{√3}{2}$
【高校数学】三角関数⑤～三角方程式の基礎～ 4-7【数学Ⅱ】
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
0≦θ<2πのとき、次の方程式を満たすθを求めよ。
(1) 2√3sinθ=-3
(2) 3tanθ+√3=0
次の方程式を満たすθを求めよ。
(1) 2√3sinθ=-3
(2) 3tanθ+√3=0
この動画を見る
0≦θ<2πのとき、次の方程式を満たすθを求めよ。
(1) 2√3sinθ=-3
(2) 3tanθ+√3=0
次の方程式を満たすθを求めよ。
(1) 2√3sinθ=-3
(2) 3tanθ+√3=0
【高校数学】三角関数4.5～例題で学ぶグラフのかき方～ 4-6【数学Ⅱ】
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
次のグラフをかけ。(丸付けは動画を参照してください)
(1) y=$\displaystyle \frac{1}{2}$cosθ
(2) y=cos(θ-$\displaystyle \frac{π}{6}$)
(3) y=cos4θ
(4) y=sin$\displaystyle \frac{θ}{2}$
(5) y=tan$\displaystyle \frac{θ}{4}$
この動画を見る
次のグラフをかけ。(丸付けは動画を参照してください)
(1) y=$\displaystyle \frac{1}{2}$cosθ
(2) y=cos(θ-$\displaystyle \frac{π}{6}$)
(3) y=cos4θ
(4) y=sin$\displaystyle \frac{θ}{2}$
(5) y=tan$\displaystyle \frac{θ}{4}$
【高校数学】三角関数④～グラフの描き方～＊裏技あり 4-5【数学Ⅱ】
京都府立医・長崎大 三角関数 高校数学 Mathematics Japanese university entrance exam
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学#京都府立医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
京都府立医科大学
$sinx+sin2x+sin3x=cosx+cos2x$
$+cos3x$を解け
長崎大学過去問題
$0 \leqq x \leqq \pi$
cos2x+4asinx+a-2=0
相異2実根をもつaの範囲
この動画を見る
京都府立医科大学
$sinx+sin2x+sin3x=cosx+cos2x$
$+cos3x$を解け
長崎大学過去問題
$0 \leqq x \leqq \pi$
cos2x+4asinx+a-2=0
相異2実根をもつaの範囲
札幌医大 三角方程式 高校数学 Mathematics Japanese university entrance exam
単元：
#三角関数とグラフ#加法定理とその応用
指導講師：
鈴木貫太郎
問題文全文(内容文)：
札幌医科大学過去問題
xに関する方程式
$cos2x+acosx+b=0$
この方程式$0 \leqq x < 2\pi$の範囲で2個の異なる実数解を持つためのa,bに関する条件
この動画を見る
札幌医科大学過去問題
xに関する方程式
$cos2x+acosx+b=0$
この方程式$0 \leqq x < 2\pi$の範囲で2個の異なる実数解を持つためのa,bに関する条件
島根大（医】三角関数 高校数学 Japanese university entrance exam questions
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
島根大学過去問題
$y=4sin2x(sinx+cosx)+\sqrt2sin(x+45^\circ)$
$0^\circ \leqq x <180^\circ$
(1)この関数の最大値とそのときのxの値
(2)この関数の最小値を求めよ。またそのときのxの値をθとするとき、$cos(θ+45^\circ)$の値を求めよ。
この動画を見る
島根大学過去問題
$y=4sin2x(sinx+cosx)+\sqrt2sin(x+45^\circ)$
$0^\circ \leqq x <180^\circ$
(1)この関数の最大値とそのときのxの値
(2)この関数の最小値を求めよ。またそのときのxの値をθとするとき、$cos(θ+45^\circ)$の値を求めよ。
弘前大 三角関数 正十角形の面積 高校数学 大学入試 Japanese university entrance exam questions
単元：
#数Ⅱ#複素数と方程式#複素数平面#三角関数#複素数#三角関数とグラフ#複素数平面#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
弘前大学過去問題
(1)$sin5θ=16sin^5θ-20sin^3θ+5sinθ$を示せ。
(2)半径1の円に内接する正十角形の面積を求めよ。
この動画を見る
弘前大学過去問題
(1)$sin5θ=16sin^5θ-20sin^3θ+5sinθ$を示せ。
(2)半径1の円に内接する正十角形の面積を求めよ。
東京海洋大学 三角関数 最大最小 高校数学 Japanese university entrance exam questions
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#三角関数とグラフ#接線と増減表・最大値・最小値#東京海洋大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
東京海洋大学過去問題
$y=2\cos^3x+2\sin^3x+3 \cos x \sin x-3$
$\cos x-3 \sin x$
$0 \leqq x \leqq 2π$のときのyの最大値、最小値およびその時のxの値
この動画を見る
東京海洋大学過去問題
$y=2\cos^3x+2\sin^3x+3 \cos x \sin x-3$
$\cos x-3 \sin x$
$0 \leqq x \leqq 2π$のときのyの最大値、最小値およびその時のxの値
和歌山大 三項間漸化式 半角の公式 高校数学 Japanese university entrance exam questions
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#三角関数#三角関数とグラフ#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#和歌山大学#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
和歌山大学過去問題
$a_1=2\sin^2\frac{θ}{2}$,$a_2=2\cosθ\sin^2\frac{θ}{2}$
$2(cos^2\frac{θ}{2})a_{n+1}=a_{n+2}+(\cosθ)a_n$
$a_n$を$\cosθ$を用いて表せ。
この動画を見る
和歌山大学過去問題
$a_1=2\sin^2\frac{θ}{2}$,$a_2=2\cosθ\sin^2\frac{θ}{2}$
$2(cos^2\frac{θ}{2})a_{n+1}=a_{n+2}+(\cosθ)a_n$
$a_n$を$\cosθ$を用いて表せ。