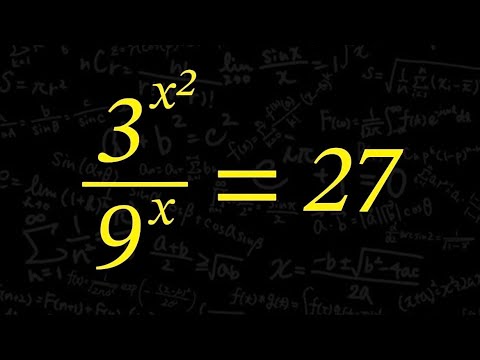指数関数
指数関数
共テ数学90％取る勉強法
単元：
#数Ⅰ#数A#数Ⅱ#数と式#２次関数#場合の数と確率#式と証明#複素数と方程式#式の計算（整式・展開・因数分解）#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#2次関数とグラフ#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#指数関数#対数関数#平均変化率・極限・導関数#数列#数列とその和（等差・等比・階差・Σ）#数学的帰納法#数学(高校生)#数B
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
共通テスト数学90％取る勉強法説明動画です
この動画を見る
共通テスト数学90％取る勉強法説明動画です
数学どうにかしたい人へ
単元：
#数Ⅰ#数A#数Ⅱ#数と式#２次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算（整式・展開・因数分解）#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#一次不等式（不等式・絶対値のある方程式・不等式）#集合と命題（集合・命題と条件・背理法）#2次方程式と2次不等式#2次関数とグラフ#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#データの分析#整数の性質#場合の数#確率#三角形の辺の比（内分・外分・二等分線）#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と２つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・Ｎ進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和（等差・等比・階差・Σ）#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数（分数関数・無理関数・逆関数と合成関数）#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化（グラフ・最大最小・方程式・不等式）#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体（オイラーの法則）#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
中学生も挑戦して どっちがでかい
単元：
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
どっちがでかい？\\
2^{266}\quad VS\quad 7^{100}
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
どっちがでかい？\\
2^{266}\quad VS\quad 7^{100}
\end{eqnarray}
$
福田の数学〜3乗根のおおよその値を知る方法〜早稲田大学2023年社会科学部第3問〜3乗根と2重根号を簡単にする
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#指数関数と対数関数#恒等式・等式・不等式の証明#指数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a=\sqrt[3]{5\sqrt{2}+7}-\sqrt[3]{5\sqrt{2}-7}$とする。
(1)$a^3$を$a$の１次式で表せ。
(2)$a$は整数であることを示せ。
(3)$b=a=\sqrt[3]{5\sqrt{2}+7}+\sqrt[3]{5\sqrt{2}-7}$
を超えない最大の整数を求めよ。
2023早稲田大学社会科学部過去問
この動画を見る
$a=\sqrt[3]{5\sqrt{2}+7}-\sqrt[3]{5\sqrt{2}-7}$とする。
(1)$a^3$を$a$の１次式で表せ。
(2)$a$は整数であることを示せ。
(3)$b=a=\sqrt[3]{5\sqrt{2}+7}+\sqrt[3]{5\sqrt{2}-7}$
を超えない最大の整数を求めよ。
2023早稲田大学社会科学部過去問
【短時間でポイントチェック!!】指数の計算の基礎(数1・化学でも使える)〔現役講師解説、数学〕
単元：
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
3rd School
問題文全文(内容文)：
①$a^2 \times a^9 \div a^5$
②$a^{-\frac{1}{2}} \times a^{\frac{2}{3}}$
③$\{(\frac{25}{16})^{-\frac{5}{4}}\}^\frac{2}{5}$
④$3^4 \times 3^{-5} \div 3^{-6}$
⑤$8^5 \times 32^{-4} \div 2^{-7}$
この動画を見る
①$a^2 \times a^9 \div a^5$
②$a^{-\frac{1}{2}} \times a^{\frac{2}{3}}$
③$\{(\frac{25}{16})^{-\frac{5}{4}}\}^\frac{2}{5}$
④$3^4 \times 3^{-5} \div 3^{-6}$
⑤$8^5 \times 32^{-4} \div 2^{-7}$
指数・対数の基本問題
単元：
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
&&3^a=7^b=441\\
&&\frac{ab}{a+b} = ?
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&3^a=7^b=441\\
&&\frac{ab}{a+b} = ?
\end{eqnarray}
$
指数方程式
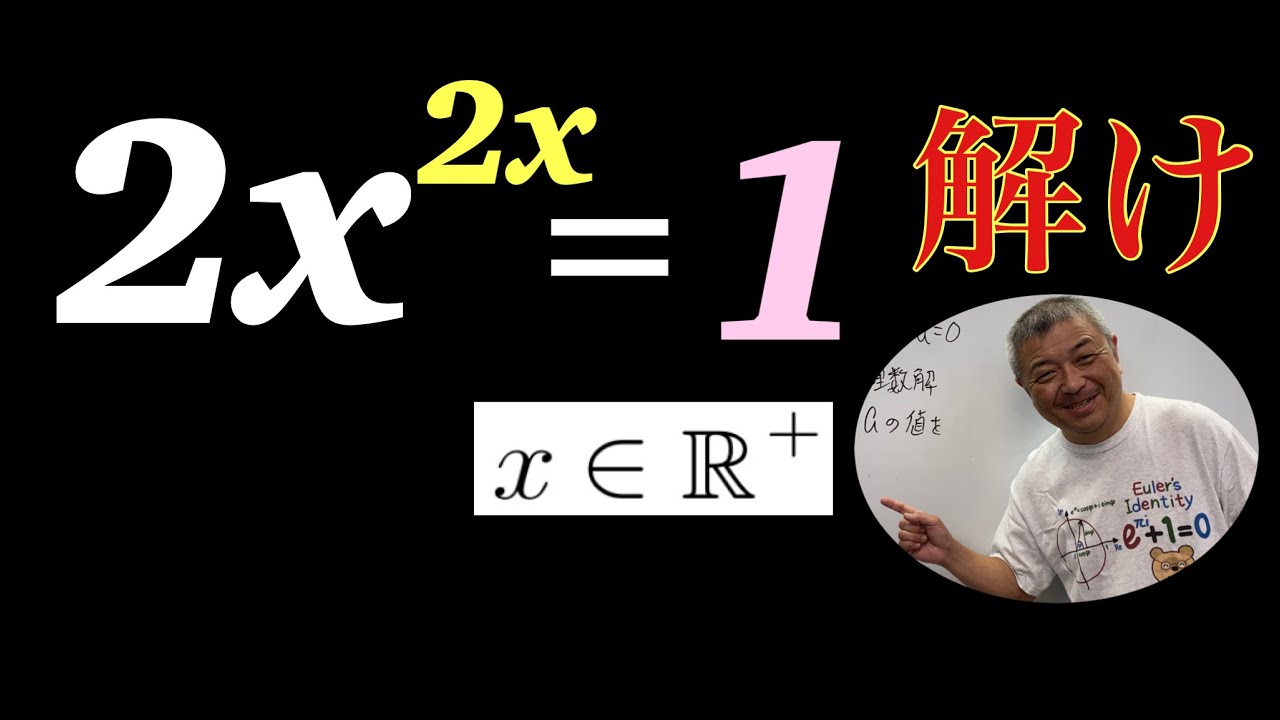
単元：
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
&&解け\\
&&x＞0\\
&&2x^{2x}=1
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&解け\\
&&x＞0\\
&&2x^{2x}=1
\end{eqnarray}
$
どっちがでかい？(５^10+12^10)vs13^10
どっちがでかい？
福田の数学〜早稲田大学2023年人間科学部第1問(3)〜指数不等式
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (3)$5^{n+5}$＞$11^n$ を満たす自然数$n$は$\boxed{\ \ エ\ \ }$個ある。
ただし、$log_511$=1.49 とする。
この動画を見る
$\Large\boxed{1}$ (3)$5^{n+5}$＞$11^n$ を満たす自然数$n$は$\boxed{\ \ エ\ \ }$個ある。
ただし、$log_511$=1.49 とする。
整数問題 ２通りの解法で
単元：
#数A#数Ⅱ#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n$ 自然数
$7^{2n-1}+9^{2n-1}+47^{2n-1}$
は63の倍数であることを示せ。
この動画を見る
$n$ 自然数
$7^{2n-1}+9^{2n-1}+47^{2n-1}$
は63の倍数であることを示せ。
これ知ってた？
これ読める？
福田の数学〜立教大学2023年理学部第1問(1)〜指数方程式
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (1)方程式$2^{x+2}$-$2^{2x+1}$+16=0 を解くと$x$=$\boxed{\ \ ア\ \ }$である。
2023立教大学理学部過去問
この動画を見る
$\Large\boxed{1}$ (1)方程式$2^{x+2}$-$2^{2x+1}$+16=0 を解くと$x$=$\boxed{\ \ ア\ \ }$である。
2023立教大学理学部過去問
引っかかりやすい指数不等式
単元：
#数Ⅰ#数Ⅱ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
不等式を解け
$-8 \leqq 2^x \leqq 8$
この動画を見る
不等式を解け
$-8 \leqq 2^x \leqq 8$
指数
単元：
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$1024 \times 4^2 = 2^▢$
(大阪教育大学附属高等学校平野校舎)
この動画を見る
$1024 \times 4^2 = 2^▢$
(大阪教育大学附属高等学校平野校舎)
指数 大阪教育大附属平野
単元：
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$1024 \times 4^2 = 2^▢$
大阪教育大学附属高等学校平野校舎
この動画を見る
$1024 \times 4^2 = 2^▢$
大阪教育大学附属高等学校平野校舎
この答えあっているのか？指数関数と等差数列 自治医科大
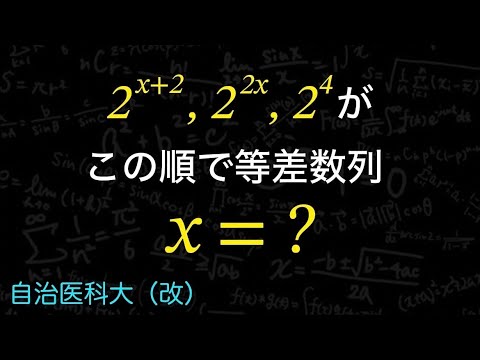
単元：
#数Ⅱ#指数関数と対数関数#指数関数#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
数学を数楽に
問題文全文(内容文)：
$2^{x+2} , 2^x , 2^4$がこの順で等差数列をなすとき、x=?
(自治医科大学(改))
この動画を見る
$2^{x+2} , 2^x , 2^4$がこの順で等差数列をなすとき、x=?
(自治医科大学(改))
指数方程式の解の配置 弘前大
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$4^x-2^{x+1}a+8a-15=0$の解が次の条件を満たす$a$の範囲を求めよ.
(1)ただ1つの実数解をもつとき
(2)相異なる2つの実数解がともに1以上のとき
弘前大過去問
この動画を見る
$4^x-2^{x+1}a+8a-15=0$の解が次の条件を満たす$a$の範囲を求めよ.
(1)ただ1つの実数解をもつとき
(2)相異なる2つの実数解がともに1以上のとき
弘前大過去問
埼玉大 ３次不等式と不等式の証明
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#指数関数と対数関数#微分法と積分法#恒等式・等式・不等式の証明#指数関数#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(1)(n+1)^3\gt n^3+(n-1)^3$を満たす最大の整数$n$を求めよ.
(2)$n=(1)$の解,$x\gt 0$のとき
$(n+1)^{x+3}\gt n^{x+3}+(n-1)^{x+3}$を証明せよ.
埼玉大過去問
この動画を見る
$(1)(n+1)^3\gt n^3+(n-1)^3$を満たす最大の整数$n$を求めよ.
(2)$n=(1)$の解,$x\gt 0$のとき
$(n+1)^{x+3}\gt n^{x+3}+(n-1)^{x+3}$を証明せよ.
埼玉大過去問
対数と不等式
単元：
#数Ⅰ#数Ⅱ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\dfrac{k-1}{k}\lt \log_{10}7 \lt \dfrac{k}{k+1}$
自然数kを求めよ.
この動画を見る
$\dfrac{k-1}{k}\lt \log_{10}7 \lt \dfrac{k}{k+1}$
自然数kを求めよ.
相加相乗平均のエレガントな証明２通り
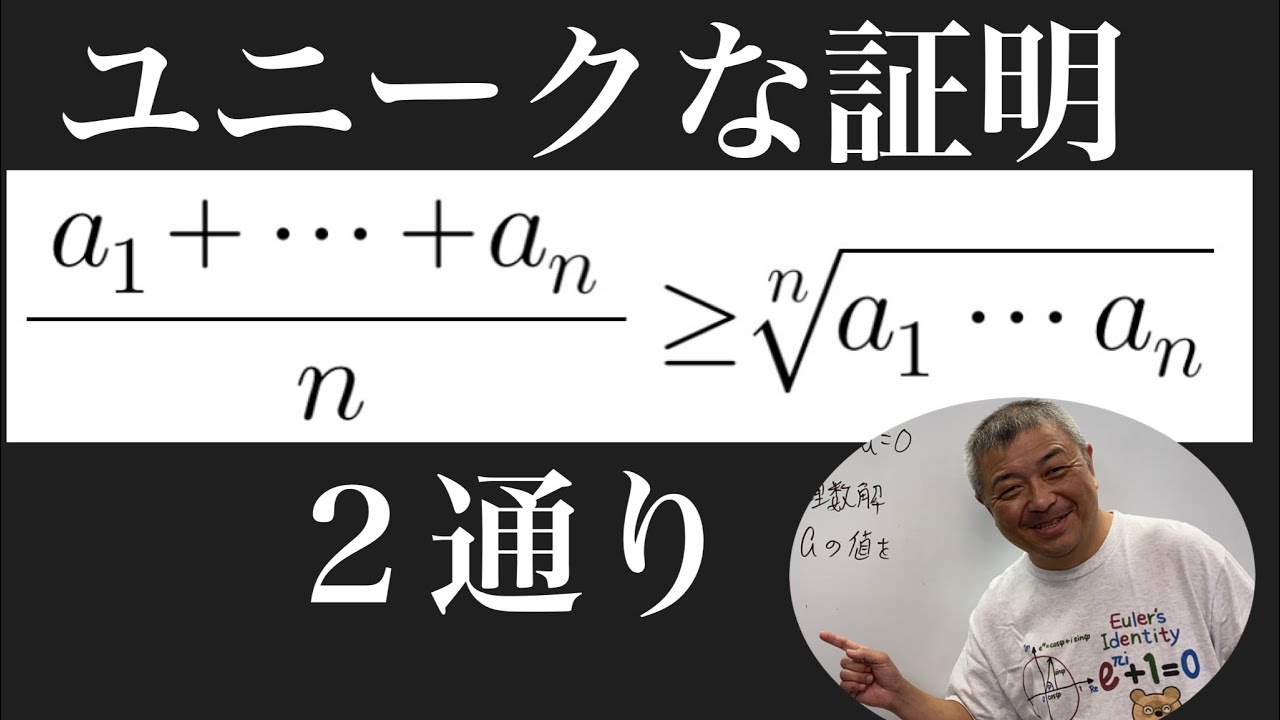
単元：
#数Ⅱ#式と証明#指数関数と対数関数#指数関数
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ \dfrac{a_1+a_2+････+a_n}{n}\geqq \sqrt[n]{a_1,a_2････a_n}$
これを求めよ.
この動画を見る
$ \dfrac{a_1+a_2+････+a_n}{n}\geqq \sqrt[n]{a_1,a_2････a_n}$
これを求めよ.
因数分解
単元：
#数Ⅰ#数Ⅱ#数と式#式の計算（整式・展開・因数分解）#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
因数分解せよ.
$9x^2+4168x+2^{15}$
この動画を見る
因数分解せよ.
$9x^2+4168x+2^{15}$
指数方程式 解は見えちゃうんだよね
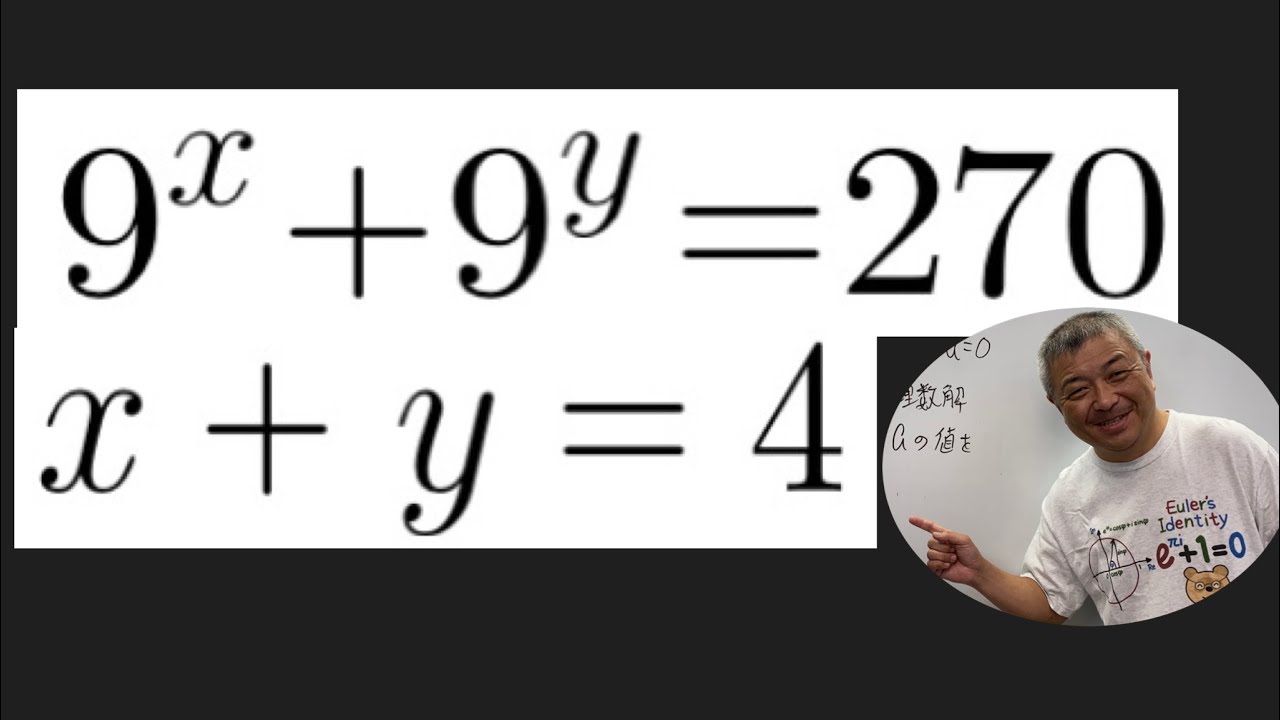
ナイスな指数方程式
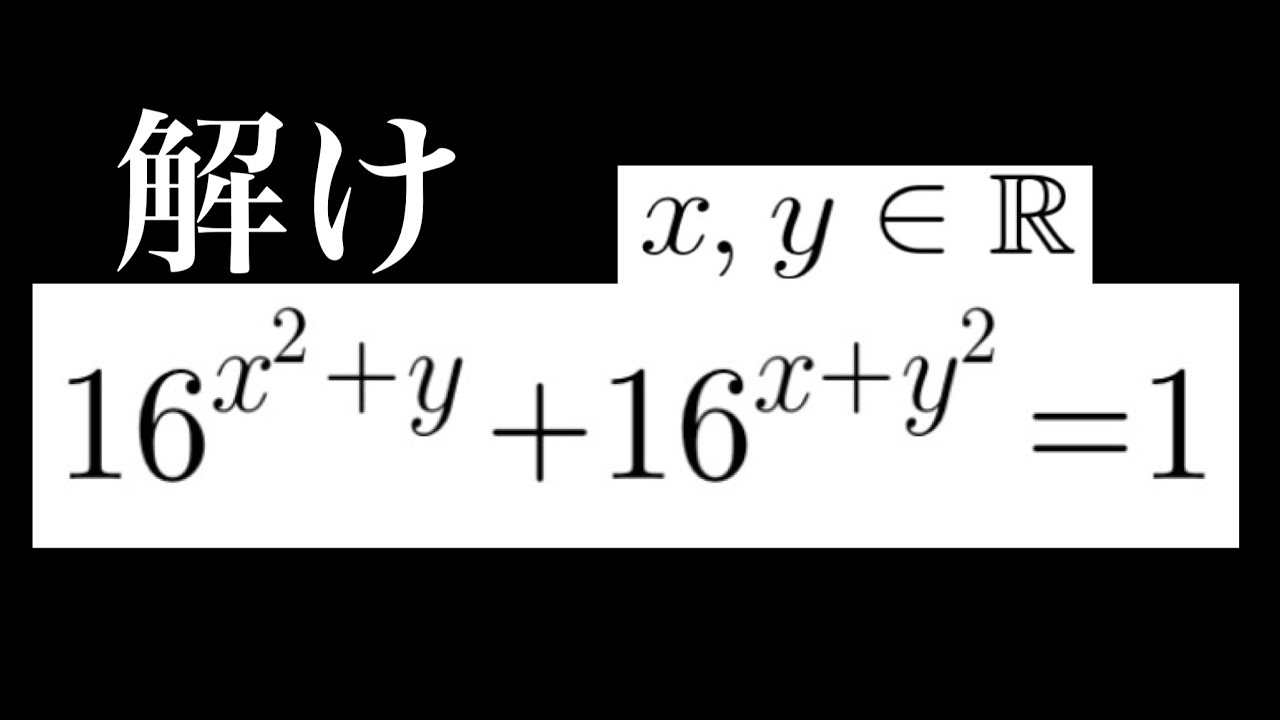
単元：
#数Ⅱ#式と証明#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
実数解を(x,y)としたとき、
$16^{x^2+y}+16^{x+y^2}=1$を求めよ.
この動画を見る
実数解を(x,y)としたとき、
$16^{x^2+y}+16^{x+y^2}=1$を求めよ.
指数の計算
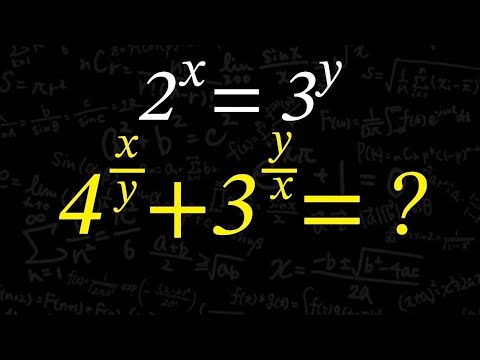
単元：
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$2^x=3^y$
$4^{\frac{x}{y}} + 3^{\frac{y}{x}}=?$
この動画を見る
$2^x=3^y$
$4^{\frac{x}{y}} + 3^{\frac{y}{x}}=?$
福田の数学〜慶應義塾大学2023年薬学部第１問(6)〜指数方程式が解をもたない条件
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (6)aを実数とする。実数xの関数f(x)=$4^x$+$4^{-x}$+a($2^x$+$2^{-x}$)+$\frac{1}{3}a^2$-1 がある。
(i)t=$2^x$+$2^{-x}$とおくときtの最小値は$\boxed{\ \ ソ\ \ }$であり、f(x)をtの式で表すと$\boxed{\ \ タ\ \ }$である。
(ii)a=-3のとき、方程式f(x)=0の解をすべて求めると、x=$\boxed{\ \ チ\ \ }$である。
(iii)方程式f(x)=0が実数解を持たないようなaの値の範囲は$\boxed{\ \ ツ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (6)aを実数とする。実数xの関数f(x)=$4^x$+$4^{-x}$+a($2^x$+$2^{-x}$)+$\frac{1}{3}a^2$-1 がある。
(i)t=$2^x$+$2^{-x}$とおくときtの最小値は$\boxed{\ \ ソ\ \ }$であり、f(x)をtの式で表すと$\boxed{\ \ タ\ \ }$である。
(ii)a=-3のとき、方程式f(x)=0の解をすべて求めると、x=$\boxed{\ \ チ\ \ }$である。
(iii)方程式f(x)=0が実数解を持たないようなaの値の範囲は$\boxed{\ \ ツ\ \ }$である。
福田の数学〜慶應義塾大学2023年薬学部第１問(3)〜３次関数と絶対不等式
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (3)a,bを実数とし、実数xの関数f(x)をf(x)=$x^3$+$ax^2$+$bx$-6とおく。
方程式f(x)=0はx=-1を解に持ち、f'(-1)=-7である。
(i)a=$\boxed{\ \ オ\ \ }$, b=$\boxed{\ \ カ\ \ }$である。
(ii)cは正の実数とする。f(x)≧3$x^2$+4(3c-1)$x$-16がx≧0において常に成立するとき、cの値の範囲は$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (3)a,bを実数とし、実数xの関数f(x)をf(x)=$x^3$+$ax^2$+$bx$-6とおく。
方程式f(x)=0はx=-1を解に持ち、f'(-1)=-7である。
(i)a=$\boxed{\ \ オ\ \ }$, b=$\boxed{\ \ カ\ \ }$である。
(ii)cは正の実数とする。f(x)≧3$x^2$+4(3c-1)$x$-16がx≧0において常に成立するとき、cの値の範囲は$\boxed{\ \ キ\ \ }$である。
2023慶應義塾大学薬学部過去問
一つとは限らない
福岡大（医）連立指数方程式
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#福岡大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x,y$は1でない正の実数であるとする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^{x+y}=y^{10} \\
y^{x+y}=x^{90}
\end{array}
\right.
\end{eqnarray}$
福岡大(医)過去問
この動画を見る
$x,y$は1でない正の実数であるとする.これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^{x+y}=y^{10} \\
y^{x+y}=x^{90}
\end{array}
\right.
\end{eqnarray}$
福岡大(医)過去問