 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
福田のおもしろ数学215〜三平方の定理が成り立つ左辺の二項のどちらか一方は4の倍数である証明

単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の数$x,y$が$x^2+y^2=z^2$を満たすとき、$x$または$y$は$4$の倍数となることを証明してください。
この動画を見る
正の数$x,y$が$x^2+y^2=z^2$を満たすとき、$x$または$y$は$4$の倍数となることを証明してください。
#千葉大学2023#定積分
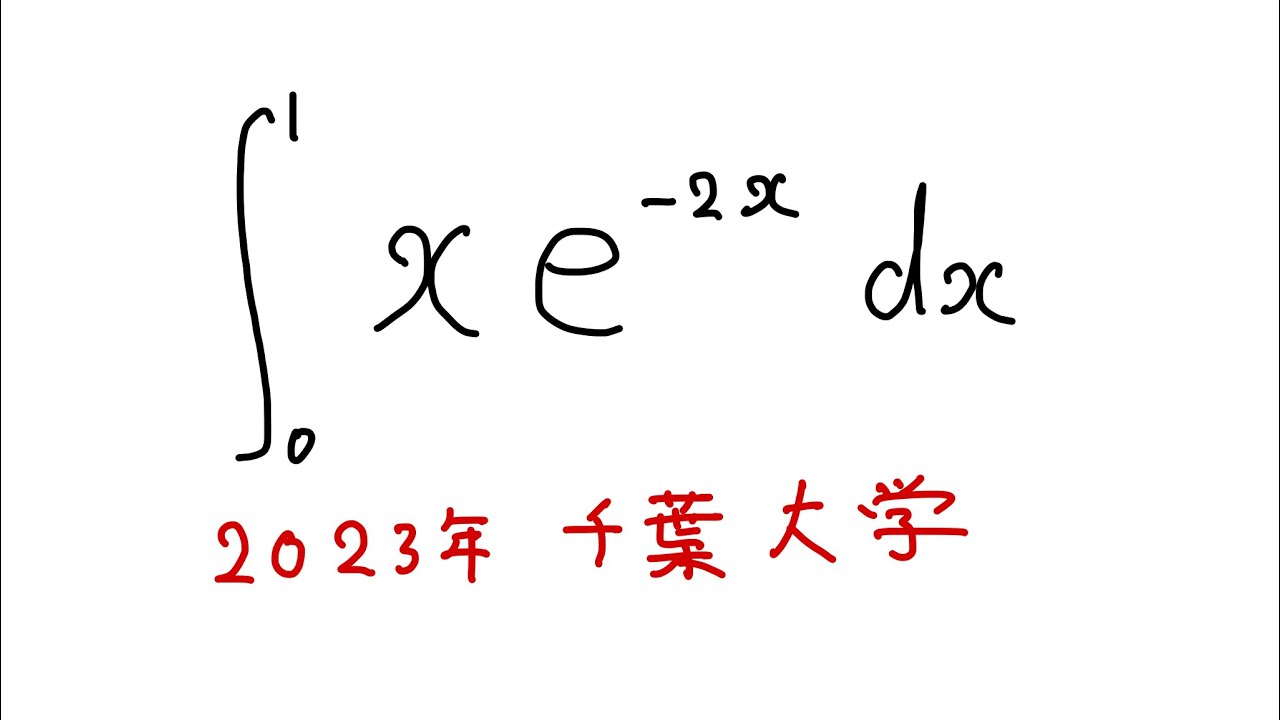
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
この動画を見る
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
#広島市立大学#不定積分#ますただ
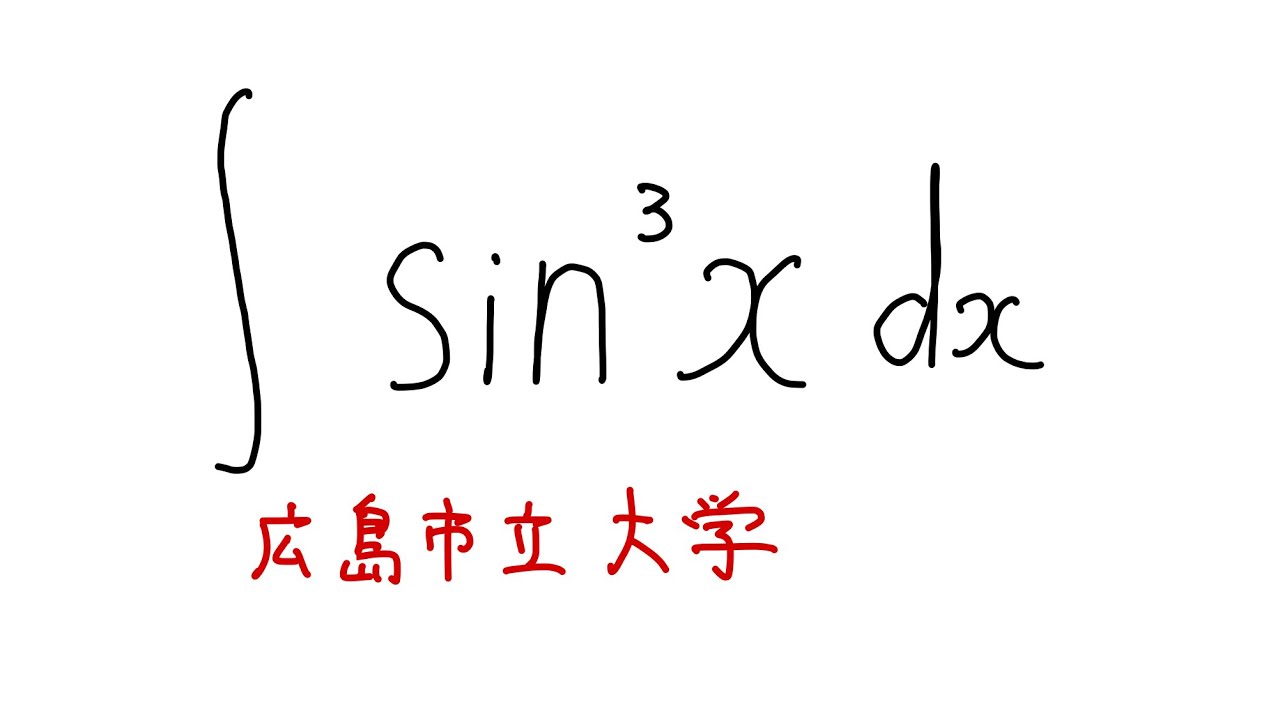
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sin^3 x$ $dx$
広島市立大過去問
この動画を見る
$\displaystyle \int \sin^3 x$ $dx$
広島市立大過去問
大学入試問題#893「難易度クソ高め」 #信州大学(2015)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \int_{2}^{x} \displaystyle \frac{t^2}{(t^2-1)^2}dt$
出典:2015年信州大学後期
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \int_{2}^{x} \displaystyle \frac{t^2}{(t^2-1)^2}dt$
出典:2015年信州大学後期
#電気通信大学2015#区分求積法#ますただ
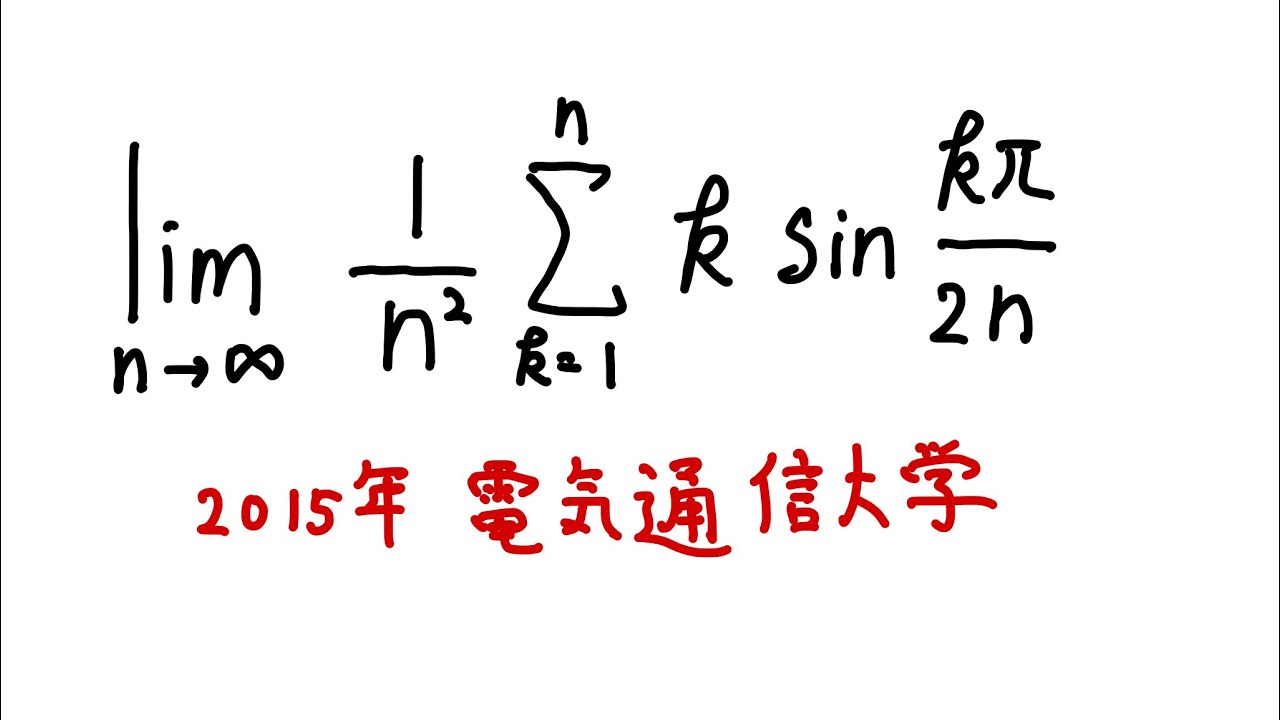
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^2}\displaystyle \sum_{k=1}^n k \sin\displaystyle \frac{k\pi}{2n}$
出典:2015年電気通信大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n^2}\displaystyle \sum_{k=1}^n k \sin\displaystyle \frac{k\pi}{2n}$
出典:2015年電気通信大学
#富山大学推薦2019#定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{x}{x^2+1} dx$
出典:2019年富山大学推薦
この動画を見る
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{x}{x^2+1} dx$
出典:2019年富山大学推薦
大学入試問題#892「数学はやっぱ根性」 #京都工芸繊維大学(2023)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \leq \theta \leq \displaystyle \frac{\pi}{4}$とする
$f(\theta)=\displaystyle \int_{0}^{\frac{\pi}{4}} \displaystyle \frac{|\sin\theta-\sin x|}{\cos^2x} dx$
出典:2023年京都工芸繊維大学
この動画を見る
$0 \leq \theta \leq \displaystyle \frac{\pi}{4}$とする
$f(\theta)=\displaystyle \int_{0}^{\frac{\pi}{4}} \displaystyle \frac{|\sin\theta-\sin x|}{\cos^2x} dx$
出典:2023年京都工芸繊維大学
福田の数学〜筑波大学2024理系第3問〜3次関数のグラフと接線

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=x(x+1)(x-1)$とする。座標平面において、曲線$y=f(x)$を$C$とし、曲線$C$上の点$(t,f(t))$における接線を$L$とする。以下の問いに答えよ。
(1) 直線$L$の方程式を$t$を用いて表せ。
(2) $t \neq 0$のとき、直線$L$と曲線$C$の共有点で、点$(t,f(t))$とは異なるものを$(a,f(a))$とする。$a$を$t$を用いて表せ。また$t$が$0$を除いた実数を動くとき、$f'(t)f'(a)$の最小値を求めよ。
(3) 次の条件Aを満たすような実数$t$の範囲を求めよ。
(A) 曲線$C$上の点$(t,f(t))$における接線が直線$L$と直交するような実数$s$が存在する。
この動画を見る
$f(x)=x(x+1)(x-1)$とする。座標平面において、曲線$y=f(x)$を$C$とし、曲線$C$上の点$(t,f(t))$における接線を$L$とする。以下の問いに答えよ。
(1) 直線$L$の方程式を$t$を用いて表せ。
(2) $t \neq 0$のとき、直線$L$と曲線$C$の共有点で、点$(t,f(t))$とは異なるものを$(a,f(a))$とする。$a$を$t$を用いて表せ。また$t$が$0$を除いた実数を動くとき、$f'(t)f'(a)$の最小値を求めよ。
(3) 次の条件Aを満たすような実数$t$の範囲を求めよ。
(A) 曲線$C$上の点$(t,f(t))$における接線が直線$L$と直交するような実数$s$が存在する。
#広島市立大学2014#不定積分#ますただ
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
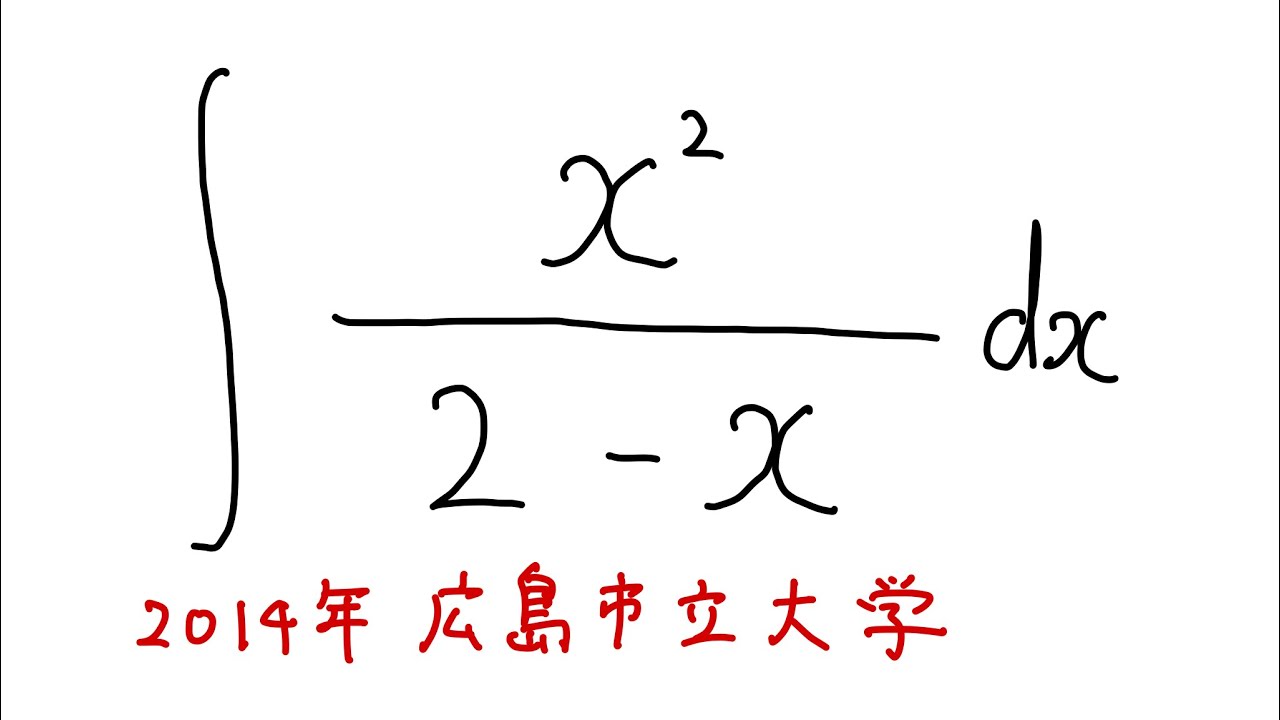
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^2}{2-x} dx$
出典:2014年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2}{2-x} dx$
出典:2014年広島市立大学
#電気通信大学2015#定積分#ますただ
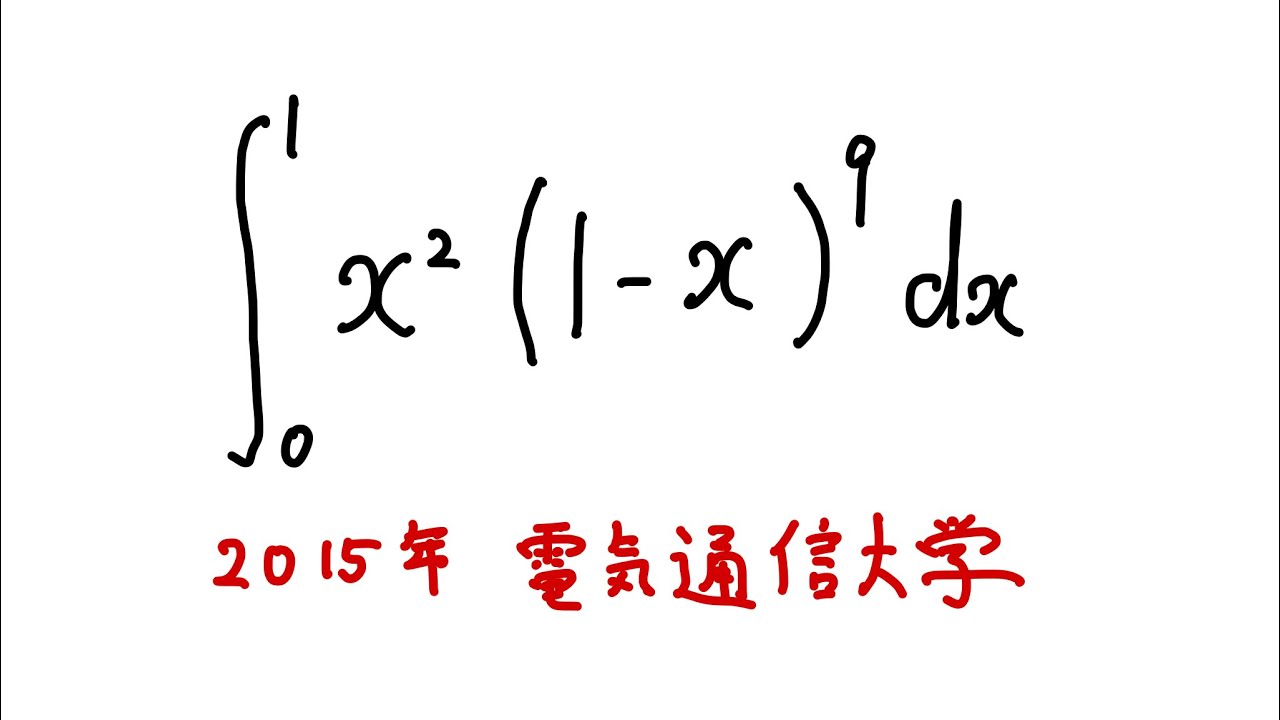
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典:2015年電気通信大学
この動画を見る
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典:2015年電気通信大学
福田のおもしろ数学212〜三角形の内角に関する不等式の証明

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\triangle \mathrm{ABC}$において、$\frac{\sin A+\sin B}{2}\leqq \sin \frac{A+B}{2} \cdots (*)$を証明してください。
この動画を見る
$\triangle \mathrm{ABC}$において、$\frac{\sin A+\sin B}{2}\leqq \sin \frac{A+B}{2} \cdots (*)$を証明してください。
福田の数学〜筑波大学2024理系第2問〜対数不等式が表す領域と面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#微分法と積分法#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
(1)$x\gt 1, y\gt 1$のとき、$\log_{ x } y+\log_{ y } x\geqq 2$を示せ。
(2)座標平面において、連立不等式$x\gt 1, y\gt 1, \log_{ x } y+\log_{ y } x\lt \frac{5}{2}$の表す領域を図示せよ。
(3)(2)の領域の中で$x^2+y^2\lt 12$を満たす部分に境界線を含めた図形を$\mathit{D}$とする。$\mathit{D}$の面積を求めよ。
この動画を見る
(1)$x\gt 1, y\gt 1$のとき、$\log_{ x } y+\log_{ y } x\geqq 2$を示せ。
(2)座標平面において、連立不等式$x\gt 1, y\gt 1, \log_{ x } y+\log_{ y } x\lt \frac{5}{2}$の表す領域を図示せよ。
(3)(2)の領域の中で$x^2+y^2\lt 12$を満たす部分に境界線を含めた図形を$\mathit{D}$とする。$\mathit{D}$の面積を求めよ。
大学入試問題#891「まだこのタイプの問題残ってた」 #信州大学(2023) #キングプロパティ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\pi}^{ \pi } \displaystyle \frac{1}{1+e^{-2\sin x}} dx$
出典:2023年信州大学
この動画を見る
$\displaystyle \int_{-\pi}^{ \pi } \displaystyle \frac{1}{1+e^{-2\sin x}} dx$
出典:2023年信州大学
#富山大学薬学部2018#不定積分
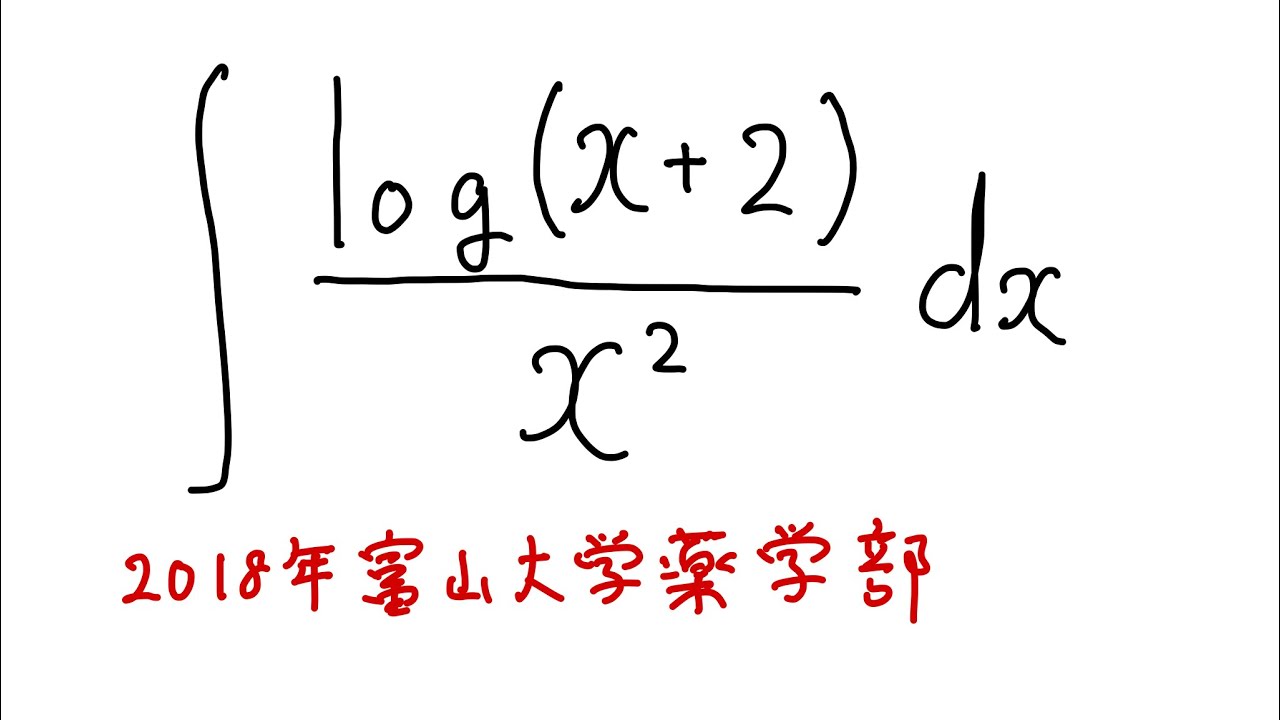
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{log(x+2)}{x^2} dx$
出典:2018年富山大学薬学部
この動画を見る
$\displaystyle \int \displaystyle \frac{log(x+2)}{x^2} dx$
出典:2018年富山大学薬学部
#数検準1級1次_4#不定積分
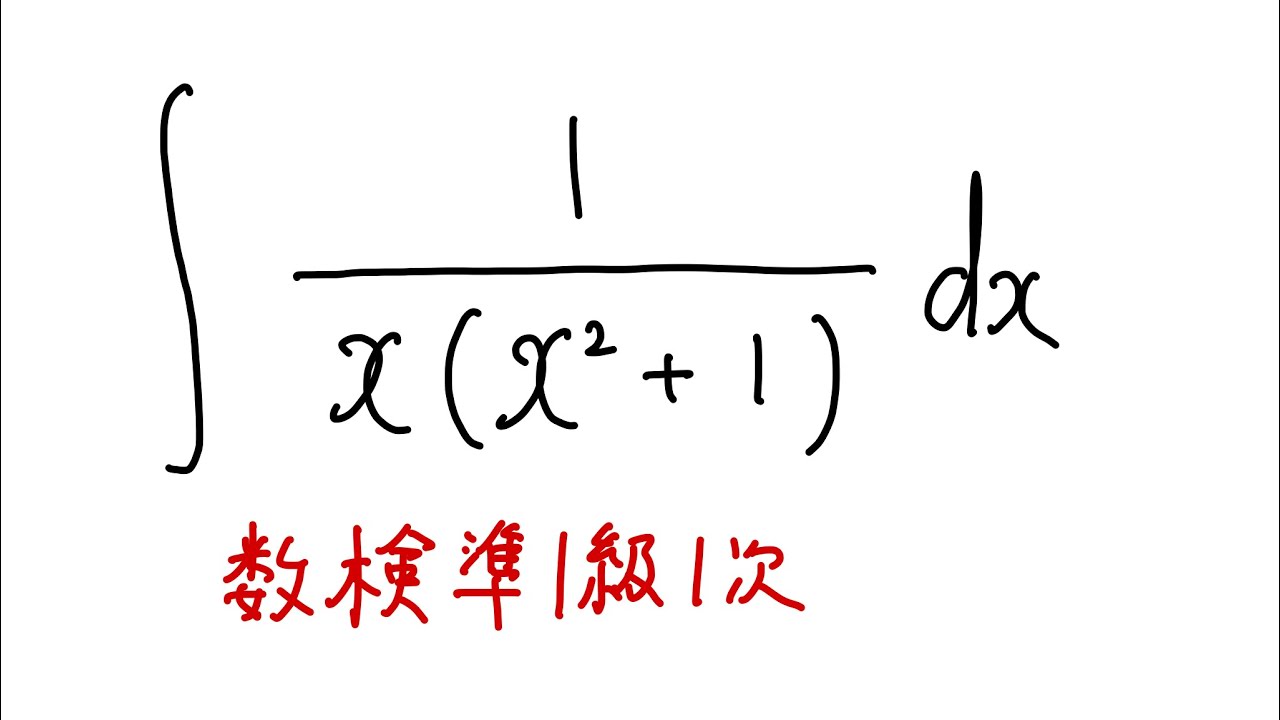
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{x(x^2+1)} dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{x(x^2+1)} dx$
出典:数検準1級1次
福田のおもしろ数学211〜証明しやすく変形するコツ〜不等式の証明

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x>0, \, y>0, \, 0 < p < 1$ のとき、$(x+y)^p < x^p+y^p$ が成り立つことを示せ。
この動画を見る
$x>0, \, y>0, \, 0 < p < 1$ のとき、$(x+y)^p < x^p+y^p$ が成り立つことを示せ。
極限

大学入試問題#890「苦手な受験生多そう」 #富山大学(2019)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=x\sqrt{ x+1 }$を導関数の定義に従って微分せよ。
出典:2019年富山大学推薦
この動画を見る
$f(x)=x\sqrt{ x+1 }$を導関数の定義に従って微分せよ。
出典:2019年富山大学推薦
√の中に8がいっぱい!!
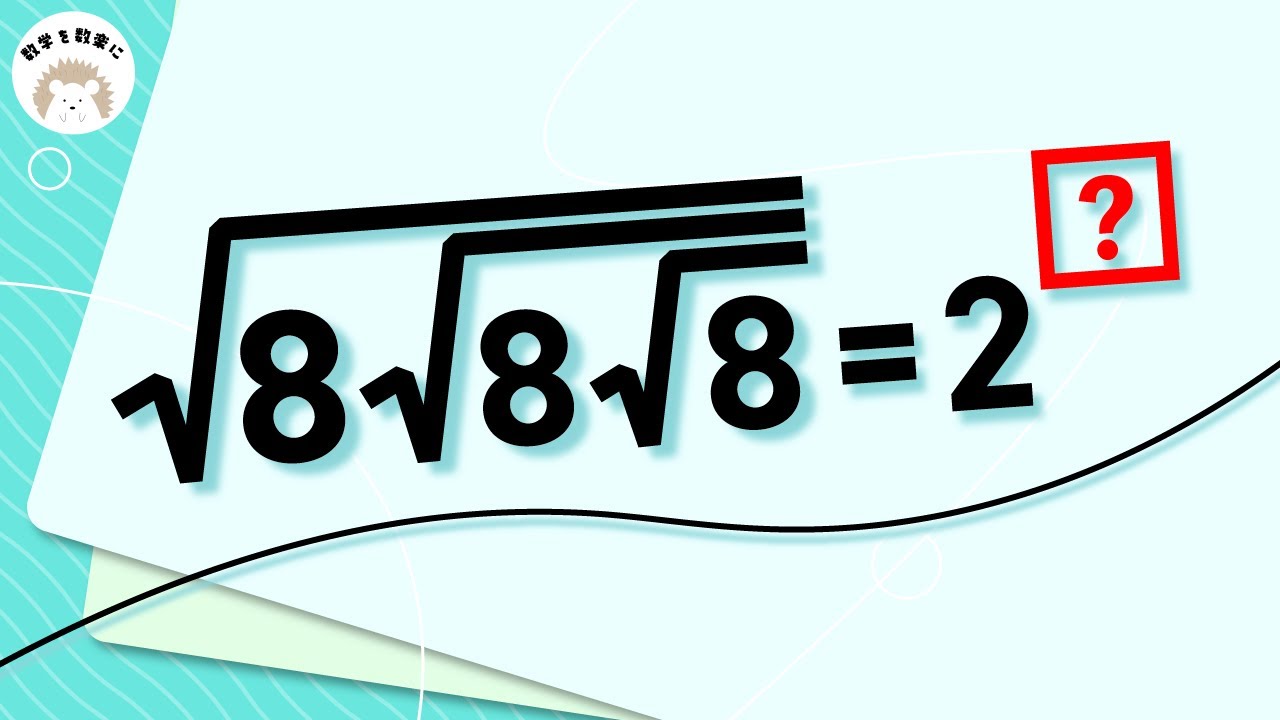
単元:
#数Ⅰ#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#指数関数
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{8\sqrt{8\sqrt8}}=2$
この動画を見る
$\sqrt{8\sqrt{8\sqrt8}}=2$
#藤田医科大学2023#定積分
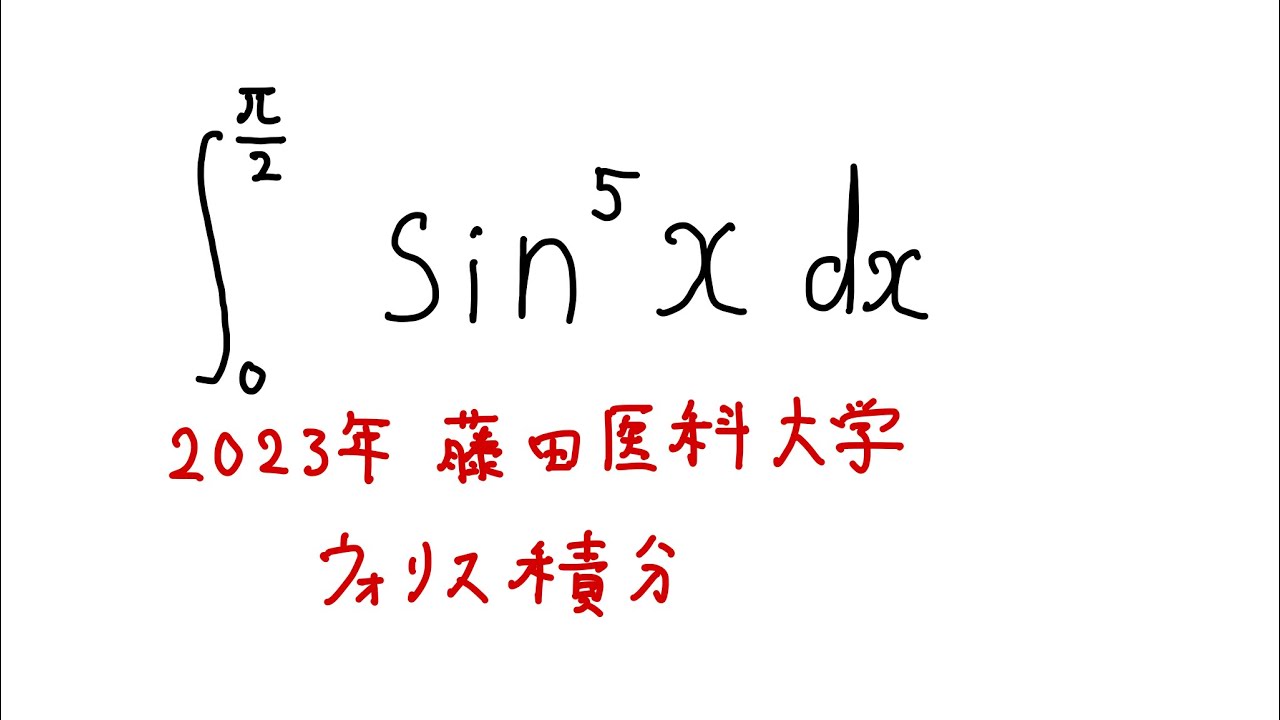
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#藤田医科大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^5x$ $dx$
出典:2023年藤田医科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^5x$ $dx$
出典:2023年藤田医科大学
【数学】中高一貫校用問題集数式・関数編:分数式を含む方程式の解法
単元:
#数Ⅱ#複素数と方程式#数学(高校生)
教材:
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の方程式を解け。
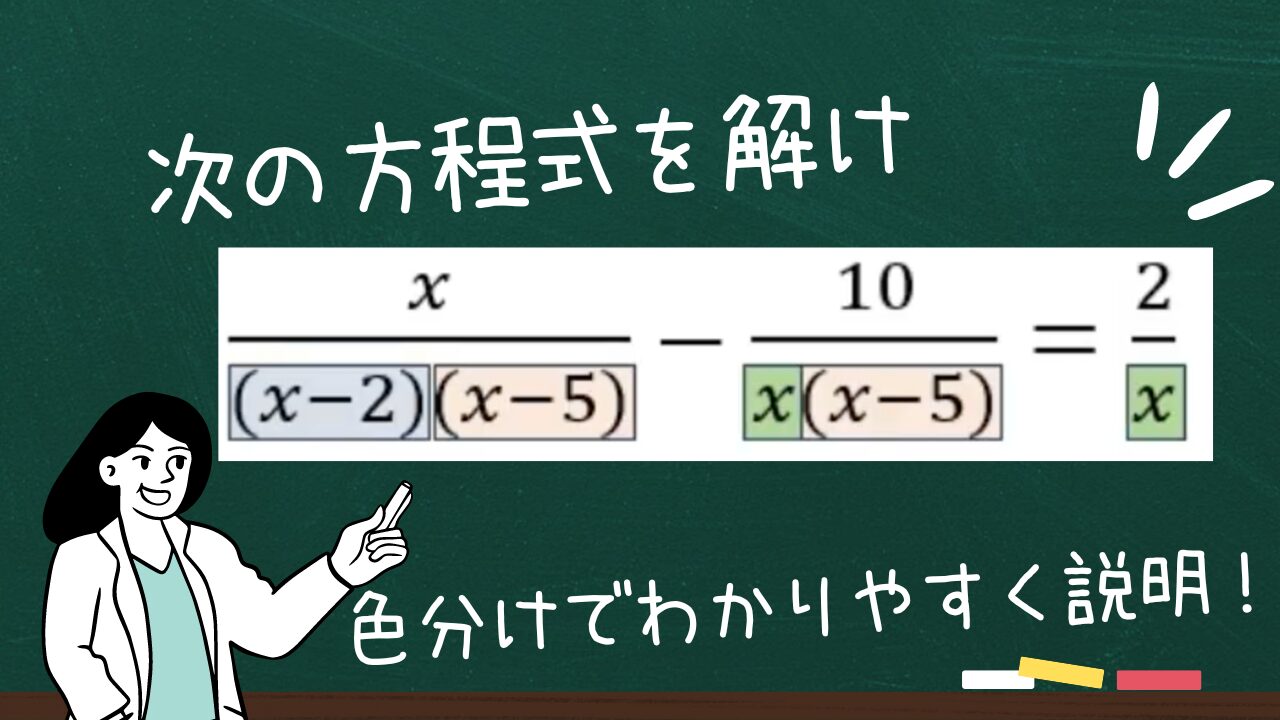
(1)$\displaystyle \frac{x}{x^2-7x+10} -\frac{10}{x^2-5x} =\frac{2}{x}$
(2)$\displaystyle \frac{x}{x^2+3x+2} =\frac{2}{x+2} -1$
この動画を見る
次の方程式を解け。
(1)$\displaystyle \frac{x}{x^2-7x+10} -\frac{10}{x^2-5x} =\frac{2}{x}$
(2)$\displaystyle \frac{x}{x^2+3x+2} =\frac{2}{x+2} -1$
#数検準1級1次_2 #不定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典:数検準1級1次
大学入試問題#889「丁寧に計算するのみ」 #富山大学(2019)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi} (\cos^2x+x^2\sin^2x) dx$
出典:2019年富山大学推薦
この動画を見る
$\displaystyle \int_{0}^{2\pi} (\cos^2x+x^2\sin^2x) dx$
出典:2019年富山大学推薦
√の中に8がいっぱい!!
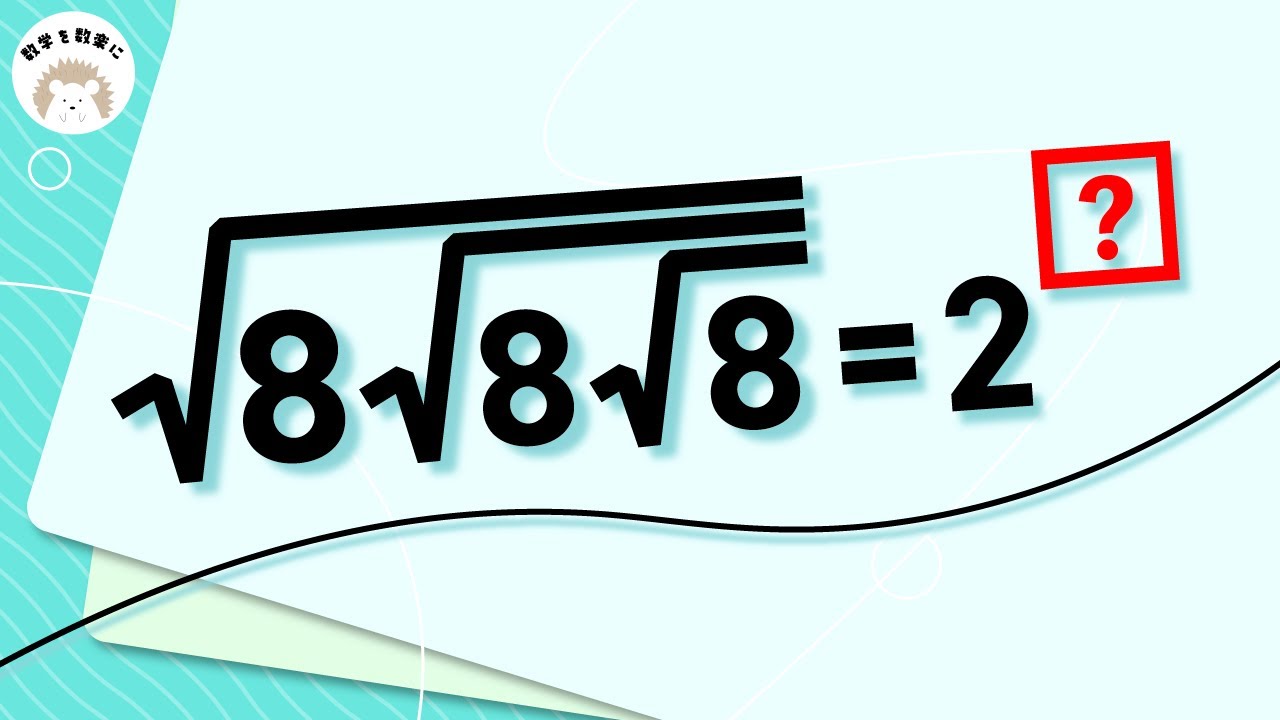
√の中に8がいっぱい!!
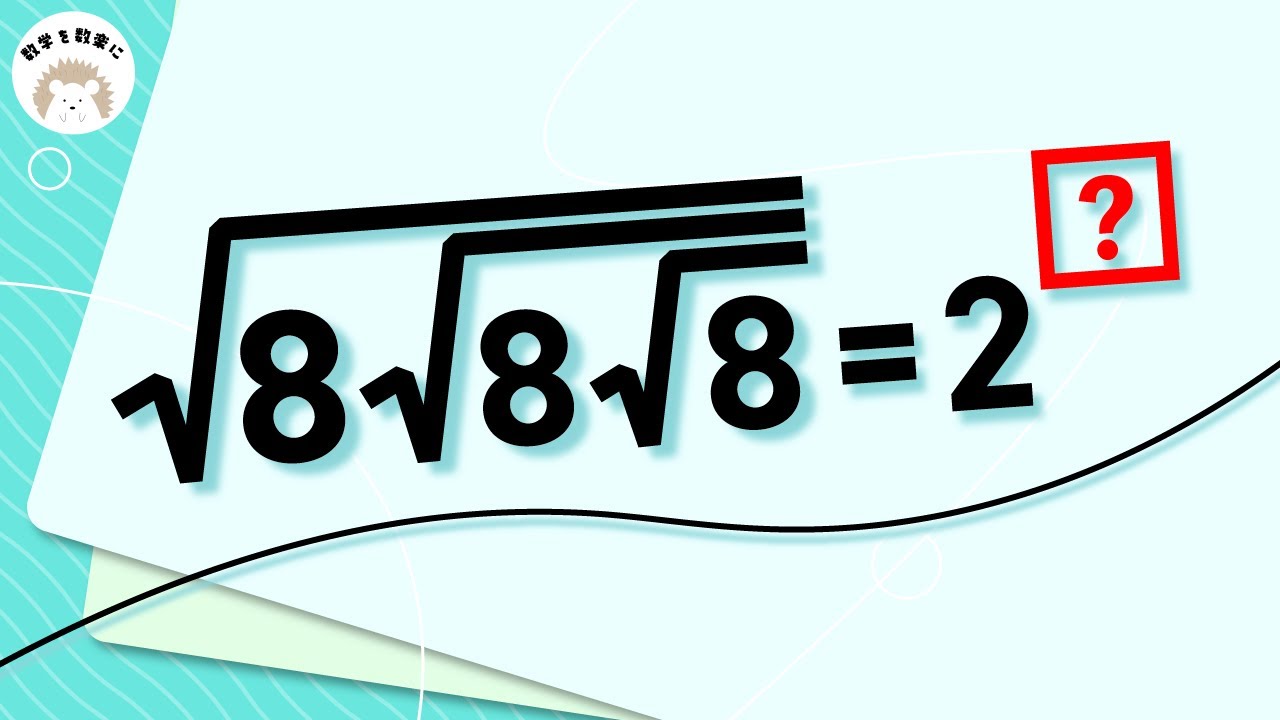
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\displaystyle \sqrt{8\sqrt{8\sqrt{8}}}=2^\boxed{?}$
この動画を見る
$\displaystyle \sqrt{8\sqrt{8\sqrt{8}}}=2^\boxed{?}$
#数検準1級1次 #7
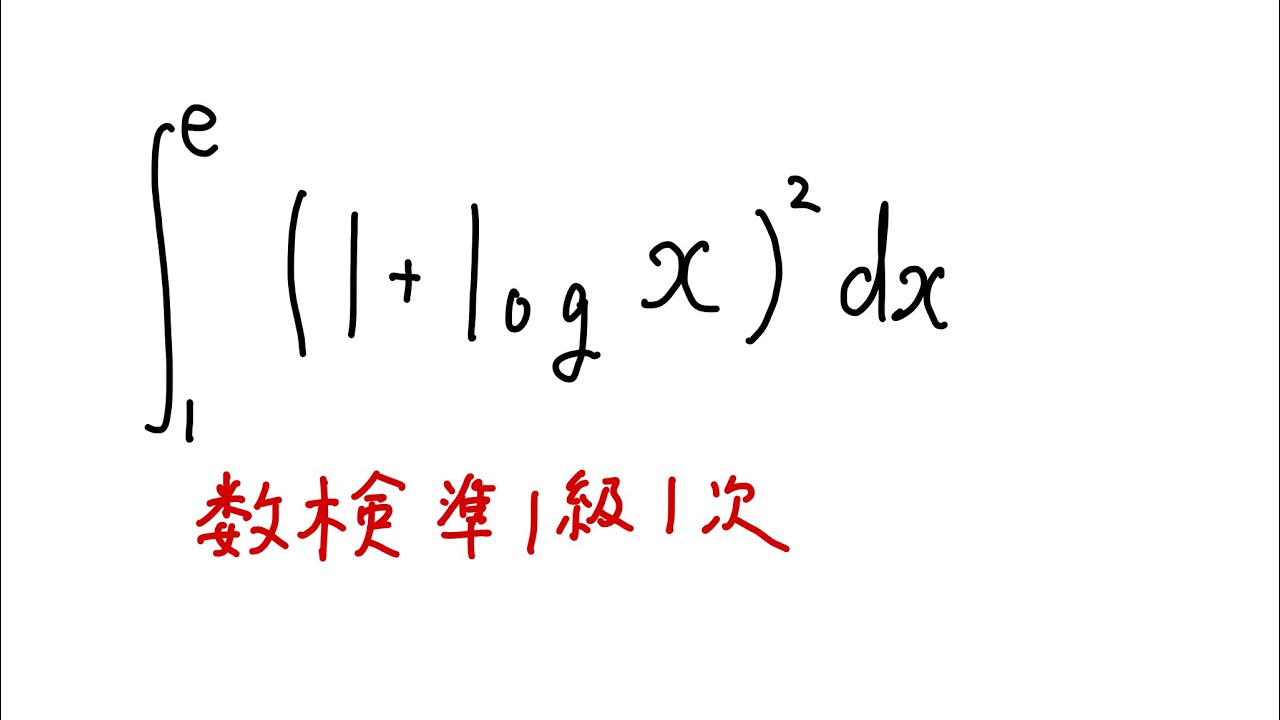
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e} (1+log x)^2$ $dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int_{1}^{e} (1+log x)^2$ $dx$
出典:数検準1級1次
#数検準1級1次-1 #定積分

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典:数検準1級1次
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{1} \displaystyle \frac{x}{x^4+2x^2+1} dx$
出典:数検準1級1次
大学入試問題#888「絶対にチャートに載ってる」 #奈良県立医科大学(2014)

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#奈良県立医科大学
指導講師:
ますただ
問題文全文(内容文):
3次方程式
$x^3-6ax^2+9a^2x-4a=0$が相異なる3つの実数解をもつような$a$の範囲を求めよ。
出典:2014年奈良県立医科大学
この動画を見る
3次方程式
$x^3-6ax^2+9a^2x-4a=0$が相異なる3つの実数解をもつような$a$の範囲を求めよ。
出典:2014年奈良県立医科大学
指数連立方程式 (高校数学)
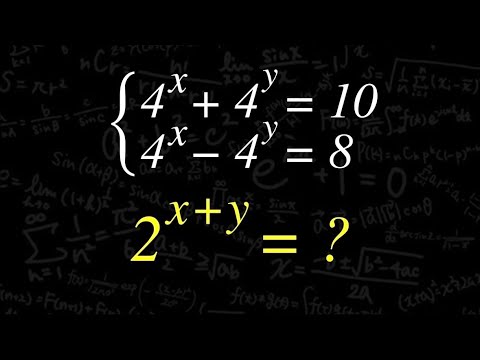
指数連立方程式 (高校数学)
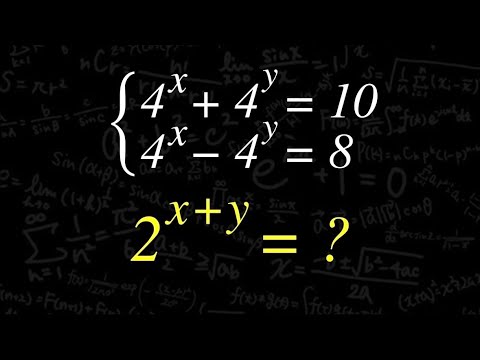
単元:
#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
4^x + 4^y = 10 \\
4^x - 4^y = 8
\end{array}
\right.
\end{eqnarray}
$2^{x+y}= ?$
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
4^x + 4^y = 10 \\
4^x - 4^y = 8
\end{array}
\right.
\end{eqnarray}
$2^{x+y}= ?$
