 関数と極限
関数と極限
 関数と極限
関数と極限
大学入試問題#122 愛知県立大学(2020) 極限
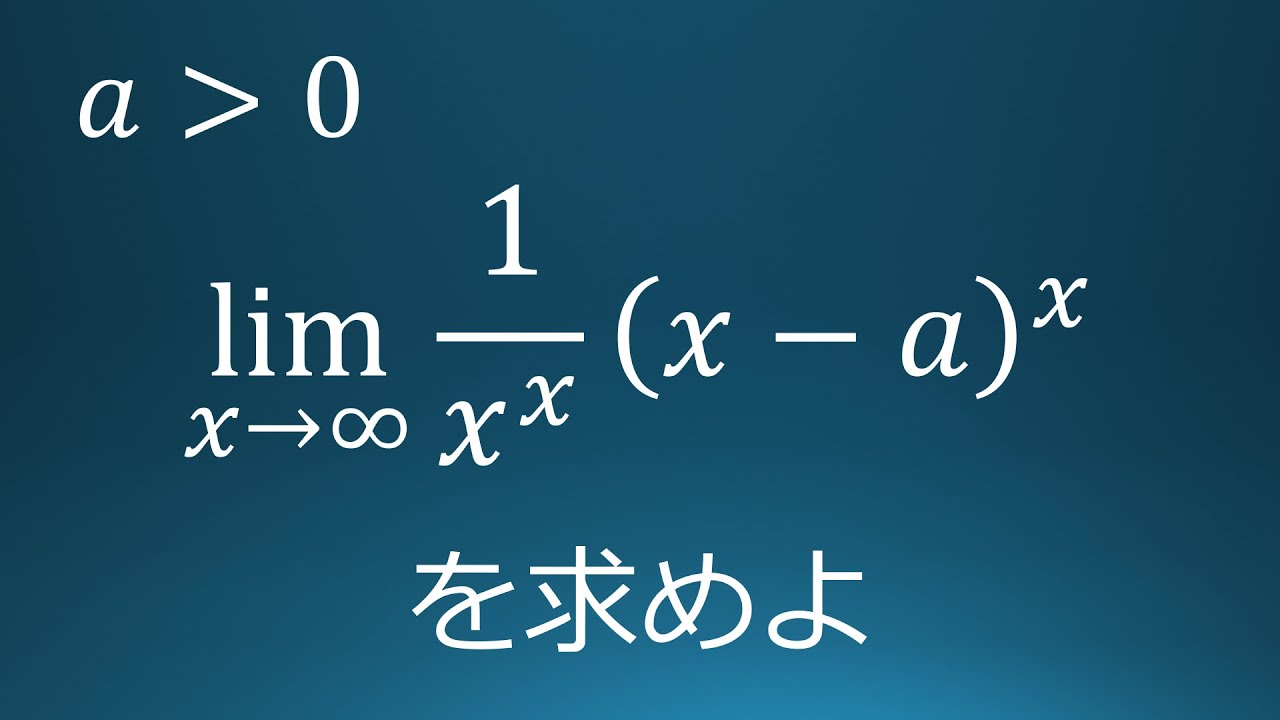
単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0$
$\displaystyle \lim_{ x \to \infty }\displaystyle \frac{1}{x^x}(x-a)^x$を求めよ。
出典:2020年愛知県立大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \lim_{ x \to \infty }\displaystyle \frac{1}{x^x}(x-a)^x$を求めよ。
出典:2020年愛知県立大学 入試問題
大学入試問題#118 防衛医科大学(2012) 区分求積法

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ \displaystyle \frac{(4n)!}{(3n)!} }$を求めよ。
出典:2012年防衛医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ \displaystyle \frac{(4n)!}{(3n)!} }$を求めよ。
出典:2012年防衛医科大学 入試問題
極限ってこういうこと?
根号を含む方程式
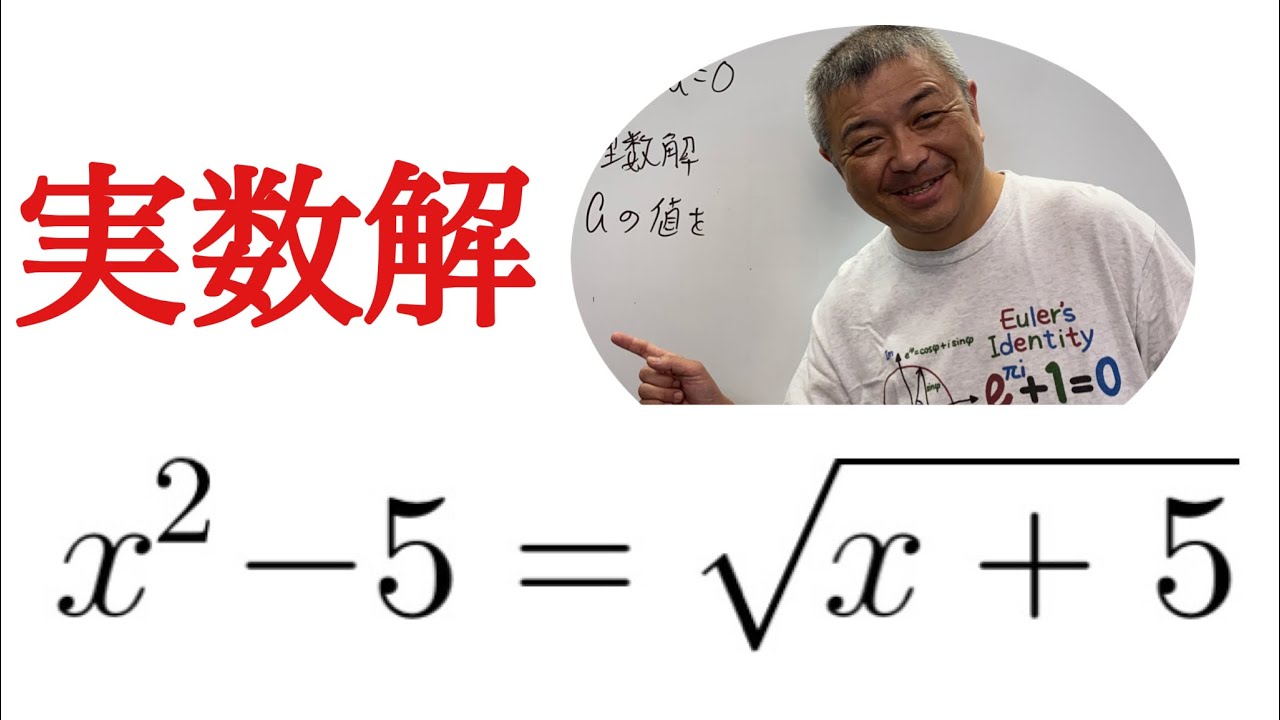
単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2-5=\sqrt{x+5}$
実数解を求めよ
この動画を見る
$x^2-5=\sqrt{x+5}$
実数解を求めよ
大学入試問題#109 大阪府立大学(2010) 無限級数

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#大阪府立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=1$
$a_{n+1}=\displaystyle \frac{n}{n+5}\ a_n$のとき
$\displaystyle \sum_{n=1}^\infty\ a_n$を求めよ
出典:2010年大阪府立大学 入試問題
この動画を見る
$a_1=1$
$a_{n+1}=\displaystyle \frac{n}{n+5}\ a_n$のとき
$\displaystyle \sum_{n=1}^\infty\ a_n$を求めよ
出典:2010年大阪府立大学 入試問題
大学入試問題#102 高知女子大学(1988) 無限級数
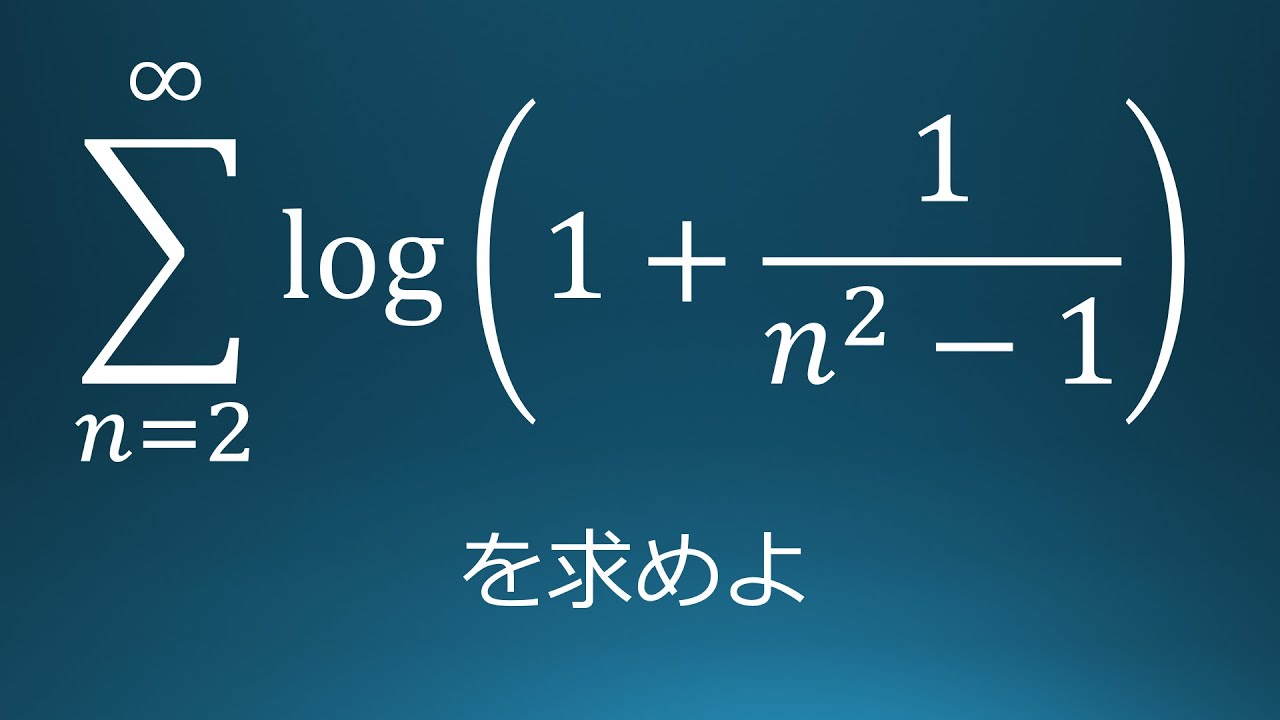
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \sum_{n=2}^\infty log(1+\displaystyle \frac{1}{n^2-1})$を求めよ。
出典:1988年高知女子大学 入試問題
この動画を見る
$\displaystyle \sum_{n=2}^\infty log(1+\displaystyle \frac{1}{n^2-1})$を求めよ。
出典:1988年高知女子大学 入試問題
大学入試問題#98 千葉大学医学部(2018) 積分・極限
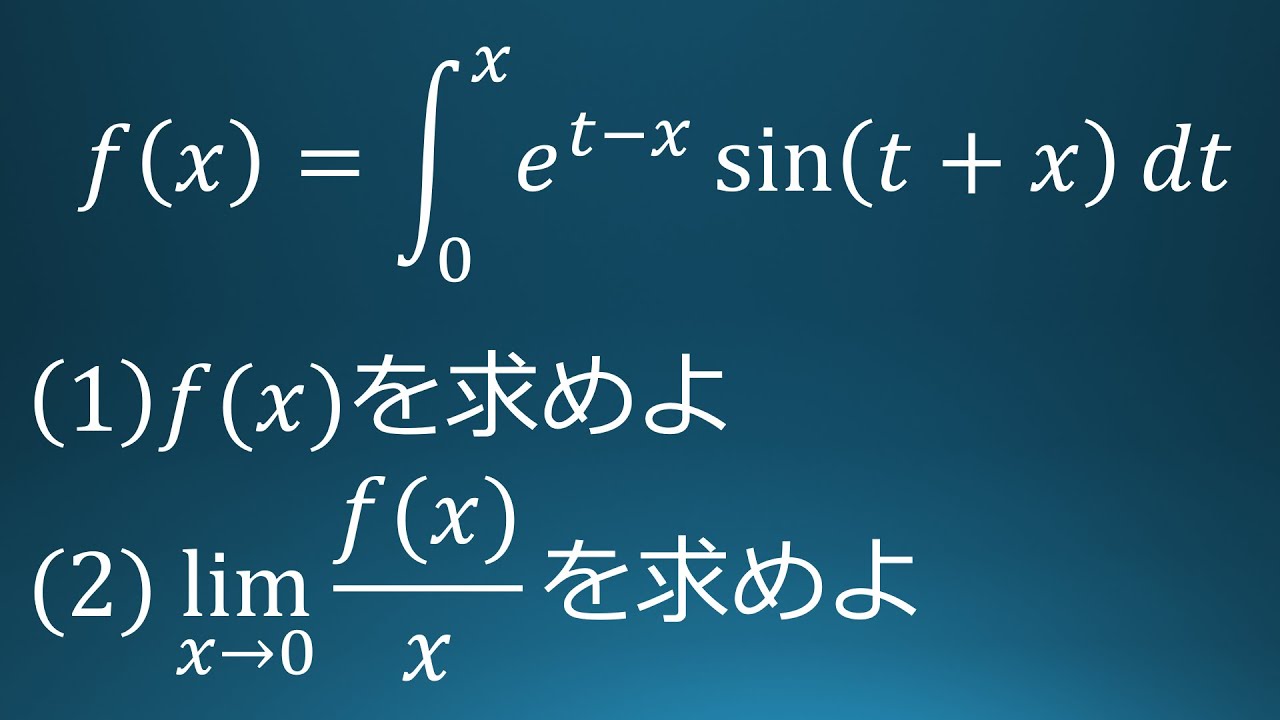
単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#不定積分#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$を求めよ。
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典:2018年千葉大学 入試問題
この動画を見る
(1)
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$を求めよ。
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典:2018年千葉大学 入試問題
大学入試問題#86 防衛医科大学(1988) 極限
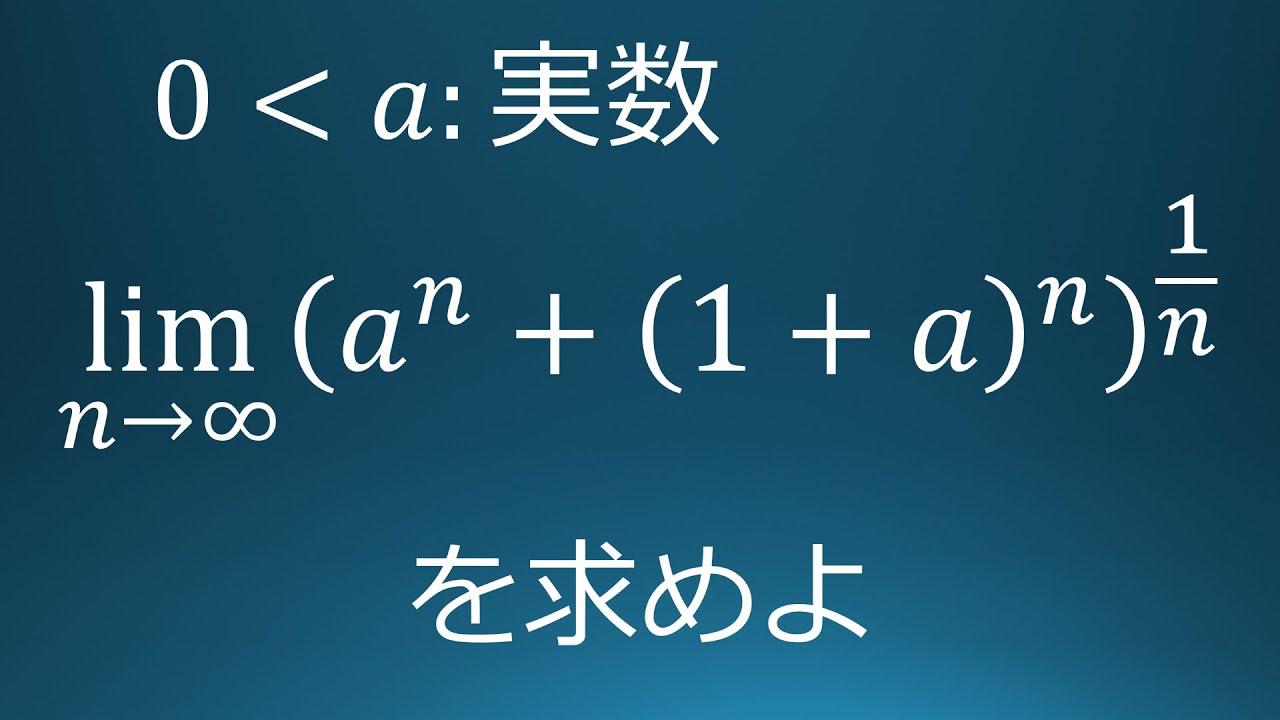
単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$0 \lt a$:実数
$\displaystyle \lim_{ n \to \infty }(a^n+(1+a)^n)^{\frac{1}{n}}$を求めよ。
出典:1988年防衛医科大学 入試問題
この動画を見る
$0 \lt a$:実数
$\displaystyle \lim_{ n \to \infty }(a^n+(1+a)^n)^{\frac{1}{n}}$を求めよ。
出典:1988年防衛医科大学 入試問題
大学入試問題#77 京都大学(2002) 数列と極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,\displaystyle \lim_{ n \to \infty }S_n=1$
$n(n-2)a_{n+1}=s_n$のとき
一般項$a_n$を求めよ。
出典:2002年京都大学 入試問題
この動画を見る
$a_1=1,\displaystyle \lim_{ n \to \infty }S_n=1$
$n(n-2)a_{n+1}=s_n$のとき
一般項$a_n$を求めよ。
出典:2002年京都大学 入試問題
【概要欄に正確な文章と説明の補足】大学入試問題#76 京都大学(2007) 数列と極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x,y$:異なる正の実数
$a_1=0$
$a_{n+1}=x a_n=s\ a_n+y^{n+1}$のとき
$\displaystyle \lim_{ n \to \infty }a_n \lt \infty$となるような$(x,y)$の範囲を図示せよ。
出典:2007年京都大学 入試問題
この動画を見る
$x,y$:異なる正の実数
$a_1=0$
$a_{n+1}=x a_n=s\ a_n+y^{n+1}$のとき
$\displaystyle \lim_{ n \to \infty }a_n \lt \infty$となるような$(x,y)$の範囲を図示せよ。
出典:2007年京都大学 入試問題
大学入試問題#74 神戸大学(1991) 数列と極限
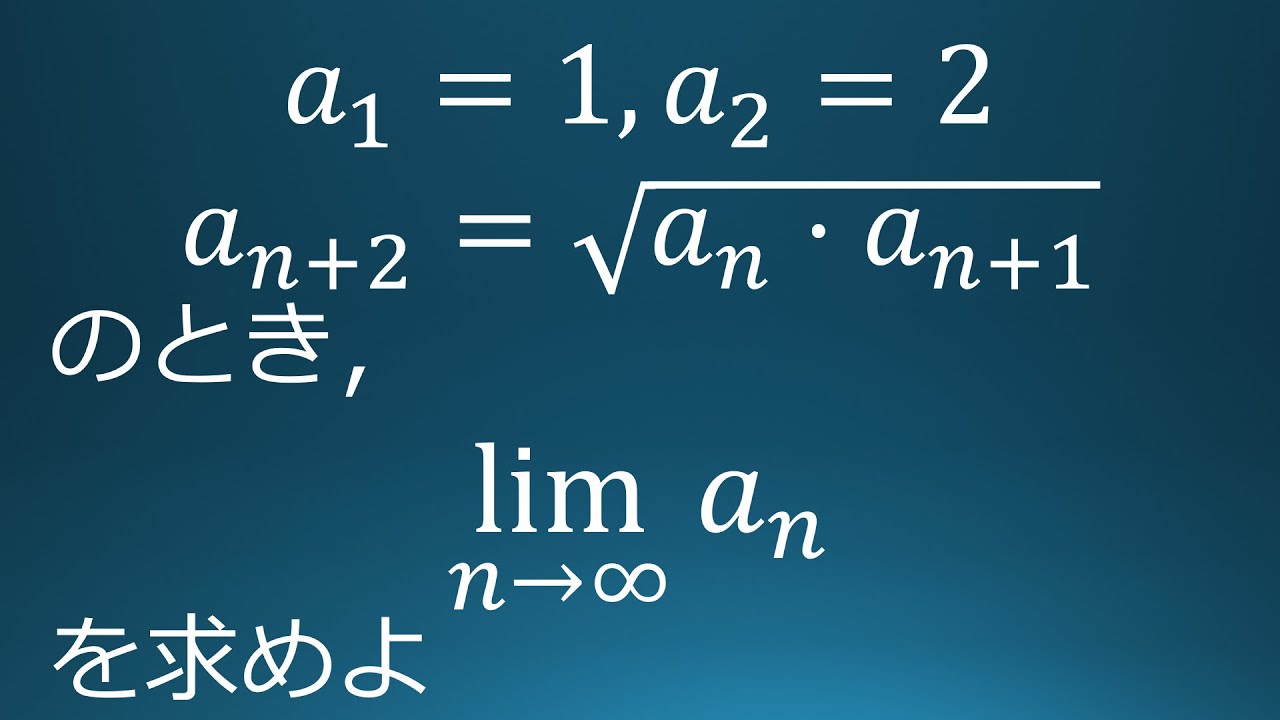
単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_n\ a_{n+1} }$のとき
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典:1991年神戸大学 入試問題
この動画を見る
$a_1=1,\ a_2=2$
$a_{n+2}=\sqrt{ a_n\ a_{n+1} }$のとき
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典:1991年神戸大学 入試問題
大学入試問題#73 京都大学(2012) 極限

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$0 \lt a$:実数
$\displaystyle \lim_{ n \to \infty }(1+a^n)^{\frac{1}{n}}$の極限を求めよ。
出典:2012年京都大学 入試問題
この動画を見る
$0 \lt a$:実数
$\displaystyle \lim_{ n \to \infty }(1+a^n)^{\frac{1}{n}}$の極限を求めよ。
出典:2012年京都大学 入試問題
こう見えても高校内容です。

原始ピタゴラス数を探せ
【数Ⅲ】極限:極限の定形不定形をマスターしよう!

単元:
#関数と極限#数列の極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
極限の考え方の基本です。変形が必要な場合と必要でない場合の違いをチェックしましょう!
この動画を見る
極限の考え方の基本です。変形が必要な場合と必要でない場合の違いをチェックしましょう!
数3を使わずに分数関数の最小値を求める

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x$は正の実数である.
$\dfrac{x^2+x+196}{x+1}$は$x=\Box$のとき,最小値$\Box$となる.
$\Box$を求めよ.
この動画を見る
$x$は正の実数である.
$\dfrac{x^2+x+196}{x+1}$は$x=\Box$のとき,最小値$\Box$となる.
$\Box$を求めよ.
#42 数検1級1次 過去問 極限値
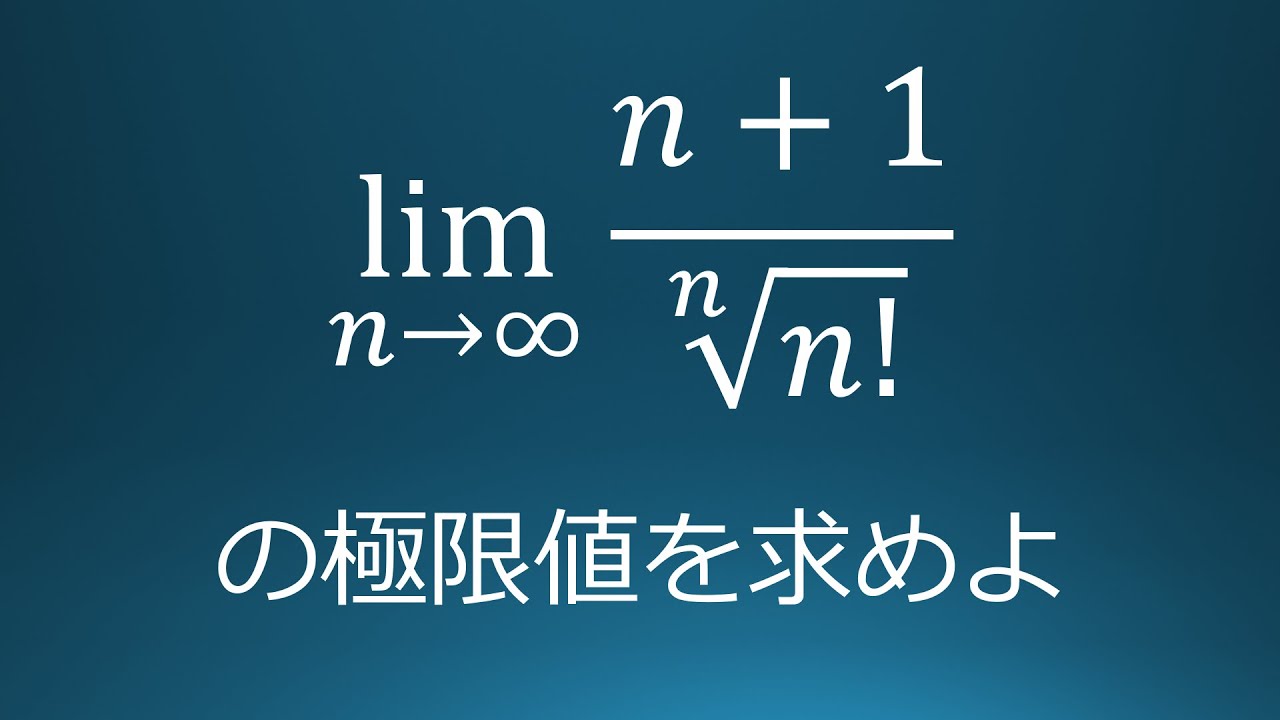
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{n+1}{\sqrt[ n ]{ n! }}$の極限値を求めよ。
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{n+1}{\sqrt[ n ]{ n! }}$の極限値を求めよ。
【数Ⅲ】極限:数列の極限と関数の極限の違いを解説します

大学入試問題#40 東京理科大学(2021) 数列と極限
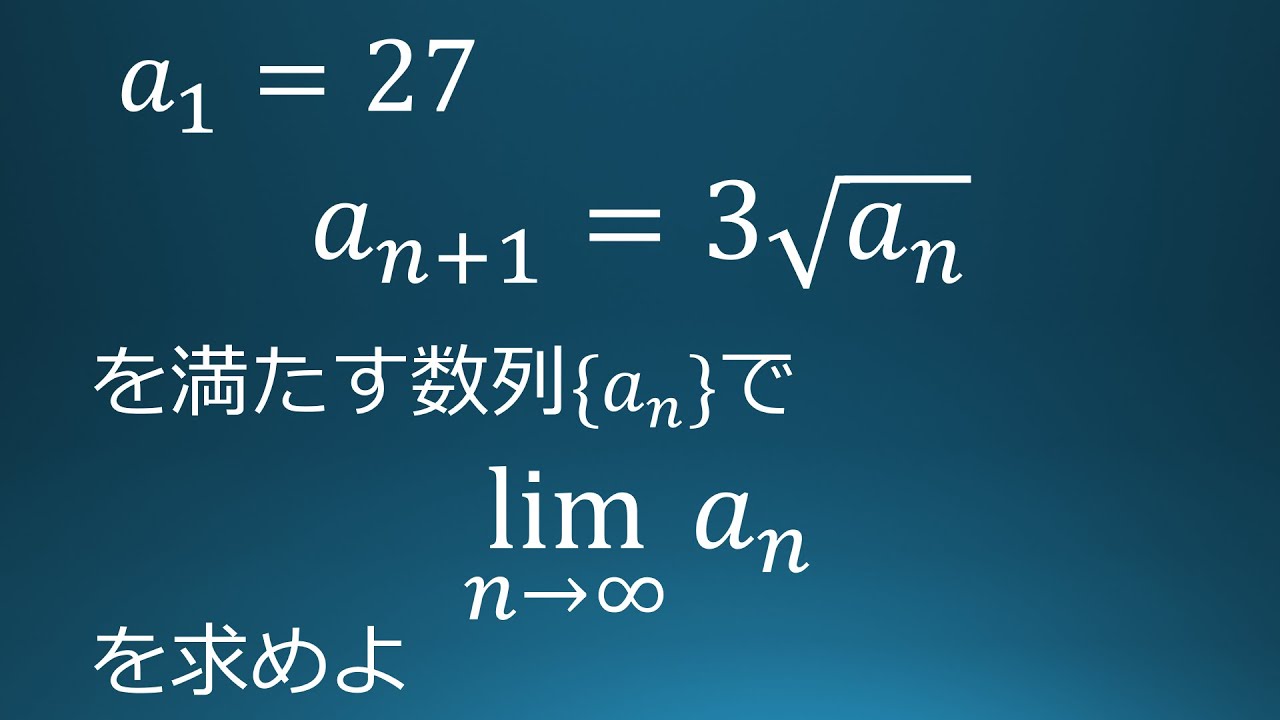
単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=27$
$a_{n+1}=3\sqrt{ a_n }$を満たす数列$\{a_n\}$において
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典:2021年東京理科大学 入試問題
この動画を見る
$a_1=27$
$a_{n+1}=3\sqrt{ a_n }$を満たす数列$\{a_n\}$において
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典:2021年東京理科大学 入試問題
福田のわかった数学〜高校3年生理系090〜グラフを描こう(12)無理関数、凹凸、漸近線

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう。(12)
$y=\sqrt[3]{x^3-x^2}$ のグラフを描け。ただし凹凸、漸近線も調べよ。
この動画を見る
数学$\textrm{III}$ グラフを描こう。(12)
$y=\sqrt[3]{x^3-x^2}$ のグラフを描け。ただし凹凸、漸近線も調べよ。
福田のわかった数学〜高校3年生理系089〜グラフを描こう(11)分数関数、凹凸、漸近線

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(11)
$y=\frac{x^3}{x^2-1}$ のグラフを描け。ただし、凹凸、漸近線も調べよ。
この動画を見る
数学$\textrm{III}$ グラフを描こう(11)
$y=\frac{x^3}{x^2-1}$ のグラフを描け。ただし、凹凸、漸近線も調べよ。
福田のわかった数学〜高校3年生理系088〜グラフを描こう(10)分数関数、凹凸、漸近線

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(10)
$y=\frac{e^x}{x-1}$
のグラフを描け。ただし凹凸、漸近線を調べよ。
この動画を見る
数学$\textrm{III}$ グラフを描こう(10)
$y=\frac{e^x}{x-1}$
のグラフを描け。ただし凹凸、漸近線を調べよ。
#22 数検1級1次 過去問 無限級数

単元:
#数学検定・数学甲子園・数学オリンピック等#関数と極限#関数の極限#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \sum_{i=1}^\infty\ \tan^{-1}\displaystyle \frac{1}{k^2+k+1}$を求めよ。
この動画を見る
$\displaystyle \sum_{i=1}^\infty\ \tan^{-1}\displaystyle \frac{1}{k^2+k+1}$を求めよ。
#21 数検1級1次 過去問 無限級数

単元:
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \sum_{k=1}^\infty\ \displaystyle \frac{k}{1+k^2+k^4}$を求めよ。
この動画を見る
$\displaystyle \sum_{k=1}^\infty\ \displaystyle \frac{k}{1+k^2+k^4}$を求めよ。
自然数無限に足すとマイナスになるみたい...

【困難は分割せよ!】関数:ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#関数(分数関数・無理関数・逆関数と合成関数)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 ラ・サール高等学校
$-1 \leqq x \leqq 2, 3 \leqq y \leqq 4$
のとき、
$x^2y-y$
の最大値と最小値を求めよ。
この動画を見る
入試問題 ラ・サール高等学校
$-1 \leqq x \leqq 2, 3 \leqq y \leqq 4$
のとき、
$x^2y-y$
の最大値と最小値を求めよ。
福田の数学〜明治大学2021年理工学部第3問〜単位ベクトルと関数の増減

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#関数と極限#微分とその応用#関数の極限#微分法#数学(高校生)#大学入試解答速報#数学#明治大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ Oを原点とする座標平面上の曲線$y=\log x$を$C$とする。正の実数$t$に対し、
曲線C上の点$P(t,\log t)$におけるCの法線Lの傾きは$\boxed{\ \ か\ \ }$である。Lに平行な
単位ベクトル$\overrightarrow{ n }$で、その$x$成分が正であるものは$\overrightarrow{ n }=(\boxed{\ \ き\ \ },\ \boxed{\ \ く\ \ })$である。
さらに、$r$を正の定数とし、点Qを$\overrightarrow{ OQ }=\overrightarrow{ OP }+r\ \overrightarrow{ n }$により定めると、
Qの座標は$(\boxed{\ \ け\ \ },\ \boxed{\ \ こ\ \ })$となる。ここで点Qのx座標とy座標をtの関数と見て、
それぞれ$X(t),\ Y(t)$とおくと$X(t),\ Y(t)$の導関数を成分とするベクトル$(X'(t),\ Y'(t))$
はrによらないベクトル$(1,\ \boxed{\ \ さ\ \ })$と平行であるか、零ベクトルである。
定数$r$の取り方によって関数$X(t)$の増減の様子は変わる。$X(t)$が区間$t \gt 0$で
常に増加するようなrの値の範囲は$\boxed{\ \ し\ \ }$である。また、$r=2\sqrt2$のとき、$X(t)$は
区間$\boxed{\ \ す\ \ } \leqq t \leqq \boxed{\ \ せ\ \ }$で減少し、区間$0 \lt t \leqq \boxed{\ \ す\ \ }$と区間$t \geqq \boxed{\ \ せ\ \ }$で増加する。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{3}}$ Oを原点とする座標平面上の曲線$y=\log x$を$C$とする。正の実数$t$に対し、
曲線C上の点$P(t,\log t)$におけるCの法線Lの傾きは$\boxed{\ \ か\ \ }$である。Lに平行な
単位ベクトル$\overrightarrow{ n }$で、その$x$成分が正であるものは$\overrightarrow{ n }=(\boxed{\ \ き\ \ },\ \boxed{\ \ く\ \ })$である。
さらに、$r$を正の定数とし、点Qを$\overrightarrow{ OQ }=\overrightarrow{ OP }+r\ \overrightarrow{ n }$により定めると、
Qの座標は$(\boxed{\ \ け\ \ },\ \boxed{\ \ こ\ \ })$となる。ここで点Qのx座標とy座標をtの関数と見て、
それぞれ$X(t),\ Y(t)$とおくと$X(t),\ Y(t)$の導関数を成分とするベクトル$(X'(t),\ Y'(t))$
はrによらないベクトル$(1,\ \boxed{\ \ さ\ \ })$と平行であるか、零ベクトルである。
定数$r$の取り方によって関数$X(t)$の増減の様子は変わる。$X(t)$が区間$t \gt 0$で
常に増加するようなrの値の範囲は$\boxed{\ \ し\ \ }$である。また、$r=2\sqrt2$のとき、$X(t)$は
区間$\boxed{\ \ す\ \ } \leqq t \leqq \boxed{\ \ せ\ \ }$で減少し、区間$0 \lt t \leqq \boxed{\ \ す\ \ }$と区間$t \geqq \boxed{\ \ せ\ \ }$で増加する。
2021明治大学理工学部過去問
福田のわかった数学〜高校3年生理系079〜グラフを描こう(1)分数関数のグラフ

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ グラフを描こう(1)
$y=\frac{x^2}{x-1}$のグラフを描け。
ただし凹凸は調べなくてよい。
この動画を見る
数学$\textrm{III}$ グラフを描こう(1)
$y=\frac{x^2}{x-1}$のグラフを描け。
ただし凹凸は調べなくてよい。
福田の数学〜明治大学2021年全学部統一入試Ⅲ第3問(1)〜定積分と極限

単元:
#関数と極限#積分とその応用#関数の極限#定積分#数学(高校生)#大学入試解答速報#数学#明治大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}} (1)\ k \gt 0$として、次の定積分を考える。
$F(k)=\int_0^1\frac{e^{kx}-1}{e^{kx}+1}\ dx$
このとき、$F(2)=\log(\boxed{\ \ ア\ \ })$となる。また、$\lim_{k \to \infty}F(k)=\boxed{\ \ イ\ \ }$である。
$\boxed{\ \ ア\ \ }$の解答群
$⓪\ \frac{e+1}{e} ①\ \frac{e^2+1}{e} ②\ \frac{e^4+1}{e} ③\ \frac{e^6+1}{e} ④\ \frac{e^8+1}{e}$
$⑤\ \frac{e+1}{2e} ⑥\ \frac{e^2+1}{2e} ⑦\ \frac{e^4+1}{2e} ⑧\ \frac{e^6+1}{2e} ⑨\ \frac{e^8+1}{2e}$
2021明治大学全統過去問
この動画を見る
${\Large\boxed{3}} (1)\ k \gt 0$として、次の定積分を考える。
$F(k)=\int_0^1\frac{e^{kx}-1}{e^{kx}+1}\ dx$
このとき、$F(2)=\log(\boxed{\ \ ア\ \ })$となる。また、$\lim_{k \to \infty}F(k)=\boxed{\ \ イ\ \ }$である。
$\boxed{\ \ ア\ \ }$の解答群
$⓪\ \frac{e+1}{e} ①\ \frac{e^2+1}{e} ②\ \frac{e^4+1}{e} ③\ \frac{e^6+1}{e} ④\ \frac{e^8+1}{e}$
$⑤\ \frac{e+1}{2e} ⑥\ \frac{e^2+1}{2e} ⑦\ \frac{e^4+1}{2e} ⑧\ \frac{e^6+1}{2e} ⑨\ \frac{e^8+1}{2e}$
2021明治大学全統過去問
【数Ⅲ】極限:関数の極限 ガウス記号を含む極限

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極限を調べよう。
(1)$\displaystyle \lim_{x\to 2}[x],$
(2)$\displaystyle \lim_{x\to 1}([2x]-[x])$
この動画を見る
次の極限を調べよう。
(1)$\displaystyle \lim_{x\to 2}[x],$
(2)$\displaystyle \lim_{x\to 1}([2x]-[x])$
