 積分とその応用
積分とその応用
 積分とその応用
積分とその応用
#茨城大学2024#定積分_2#元高校教員
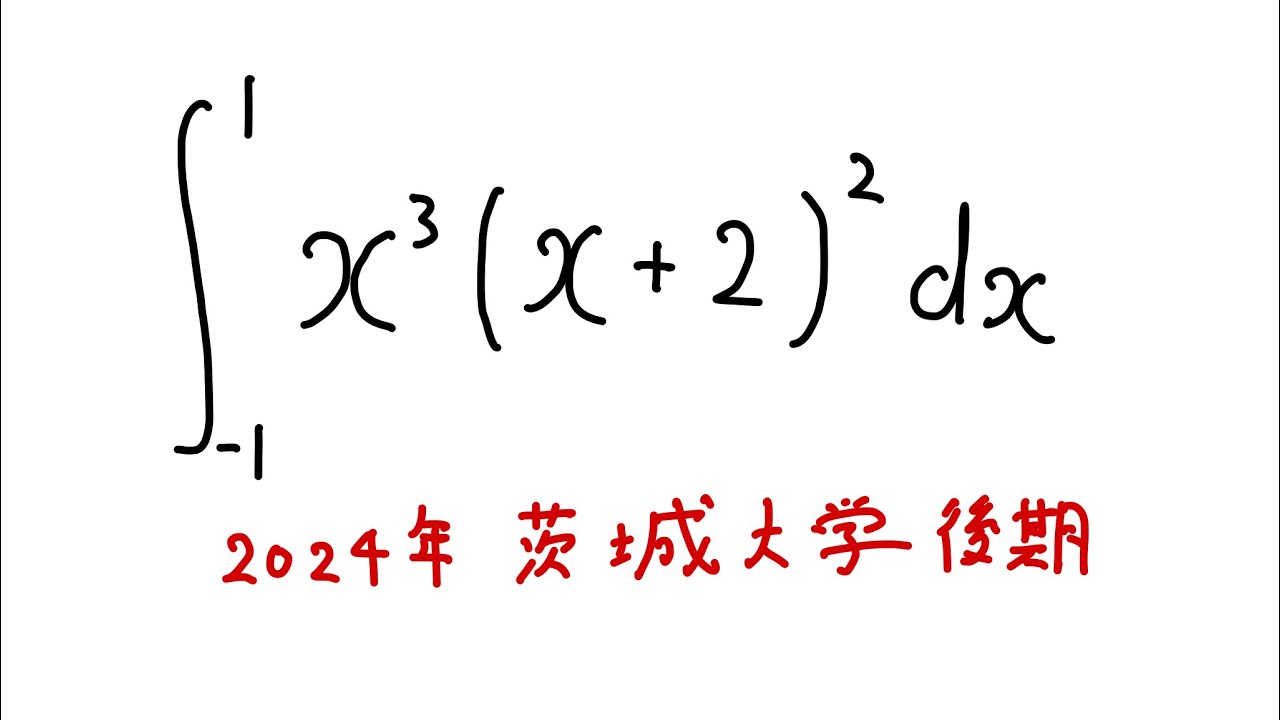
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} x^3(x+2)^2 dx$
出典:2024年茨城大学後期
この動画を見る
$\displaystyle \int_{-1}^{1} x^3(x+2)^2 dx$
出典:2024年茨城大学後期
大学入試問題#616「これは理系が解くと逆にはまるかも」 名古屋大学(1963)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x \gt y$とする
$x+y=6,\ xy=4$のとき
$\displaystyle \frac{\sqrt{ x }-\sqrt{ y }}{\sqrt{ x }+\sqrt{ y }}$の値を求めよ。
出典:1963年名古屋大学 入試問題
この動画を見る
$x \gt y$とする
$x+y=6,\ xy=4$のとき
$\displaystyle \frac{\sqrt{ x }-\sqrt{ y }}{\sqrt{ x }+\sqrt{ y }}$の値を求めよ。
出典:1963年名古屋大学 入試問題
福田の数学〜中央大学2024理工学部第1問〜3つの関数の大小関係と絶対不等式

単元:
#数Ⅰ#2次関数#2次関数とグラフ#微分とその応用#積分とその応用#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$a$ を $1$ 以上の実数、$b$ を実数とし、関数 $f(x), \, g(x), \, h(x)$ を以下で定める。
$\displaystyle f(x)=-|2|x|-1|, \quad g(x)=ax+b, \quad h(x)=e^x$
$(1)$ すべての実数 $x$ に対して $f(x) \leq g(x)$ が成り立つ。$(a, \, b)$ の範囲は、条件 $a \geq 1$ の下では、$b \geq 1$ のとき $a \leq \fbox{ア}$ であり、$\frac{1}{2} \leq b \leq 1$ のとき $a \leq \fbox{イ}$ である。$b < \frac{1}{2}$ のとき条件を満たす $a$ は存在しない。
$(2)$ 実数$p$ に対し、$x=p$ における $y=h(x)$ の接線の方程式は $y=\fbox{ウ}$ である。したがって $a=e^p$ のとき、すべての実数 $x$ に対して $g(x) \leq h(x)$ が成り立つのは $b \leq \fbox{エ}$ のときであり、これは $a$ と $b$ の関係式として $b \leq \fbox{オ}$
$(3)$ すべての実数 $x$ に対し、$f(x) \leq g(x) \leq h(x)$ が成り立つような $(a, \, b)$ 全体のなす領域を $D$ とする。$D$ における $a$ の最大値は $\fbox{カ}$ である。また、$D$ の面積は $\fbox{キ}$ である。
この動画を見る
$a$ を $1$ 以上の実数、$b$ を実数とし、関数 $f(x), \, g(x), \, h(x)$ を以下で定める。
$\displaystyle f(x)=-|2|x|-1|, \quad g(x)=ax+b, \quad h(x)=e^x$
$(1)$ すべての実数 $x$ に対して $f(x) \leq g(x)$ が成り立つ。$(a, \, b)$ の範囲は、条件 $a \geq 1$ の下では、$b \geq 1$ のとき $a \leq \fbox{ア}$ であり、$\frac{1}{2} \leq b \leq 1$ のとき $a \leq \fbox{イ}$ である。$b < \frac{1}{2}$ のとき条件を満たす $a$ は存在しない。
$(2)$ 実数$p$ に対し、$x=p$ における $y=h(x)$ の接線の方程式は $y=\fbox{ウ}$ である。したがって $a=e^p$ のとき、すべての実数 $x$ に対して $g(x) \leq h(x)$ が成り立つのは $b \leq \fbox{エ}$ のときであり、これは $a$ と $b$ の関係式として $b \leq \fbox{オ}$
$(3)$ すべての実数 $x$ に対し、$f(x) \leq g(x) \leq h(x)$ が成り立つような $(a, \, b)$ 全体のなす領域を $D$ とする。$D$ における $a$ の最大値は $\fbox{カ}$ である。また、$D$ の面積は $\fbox{キ}$ である。
#高専数学_11#定積分#元高専教員
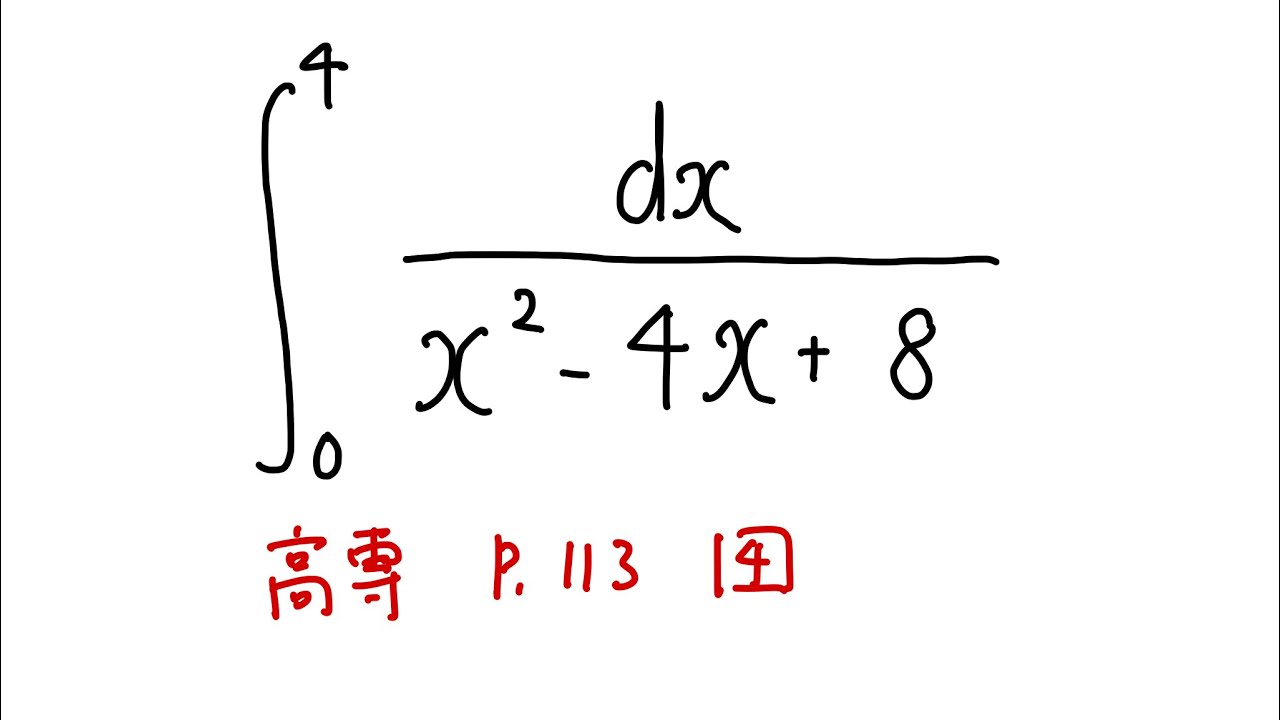
単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{4} \displaystyle \frac{dx}{x^2-4x+8}$
この動画を見る
$\displaystyle \int_{0}^{4} \displaystyle \frac{dx}{x^2-4x+8}$
#茨城大学2024_1#定積分
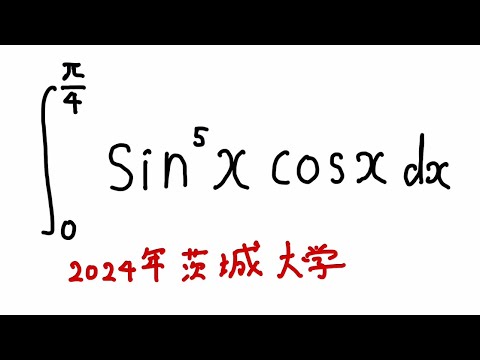
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin^5x\cos x$ $dx$
出典:2024年茨城大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \sin^5x\cos x$ $dx$
出典:2024年茨城大学
#高専数学_10#不定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{(x-2)^2} dx$
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{(x-2)^2} dx$
#高専数学_9#不定積分#元高専教員
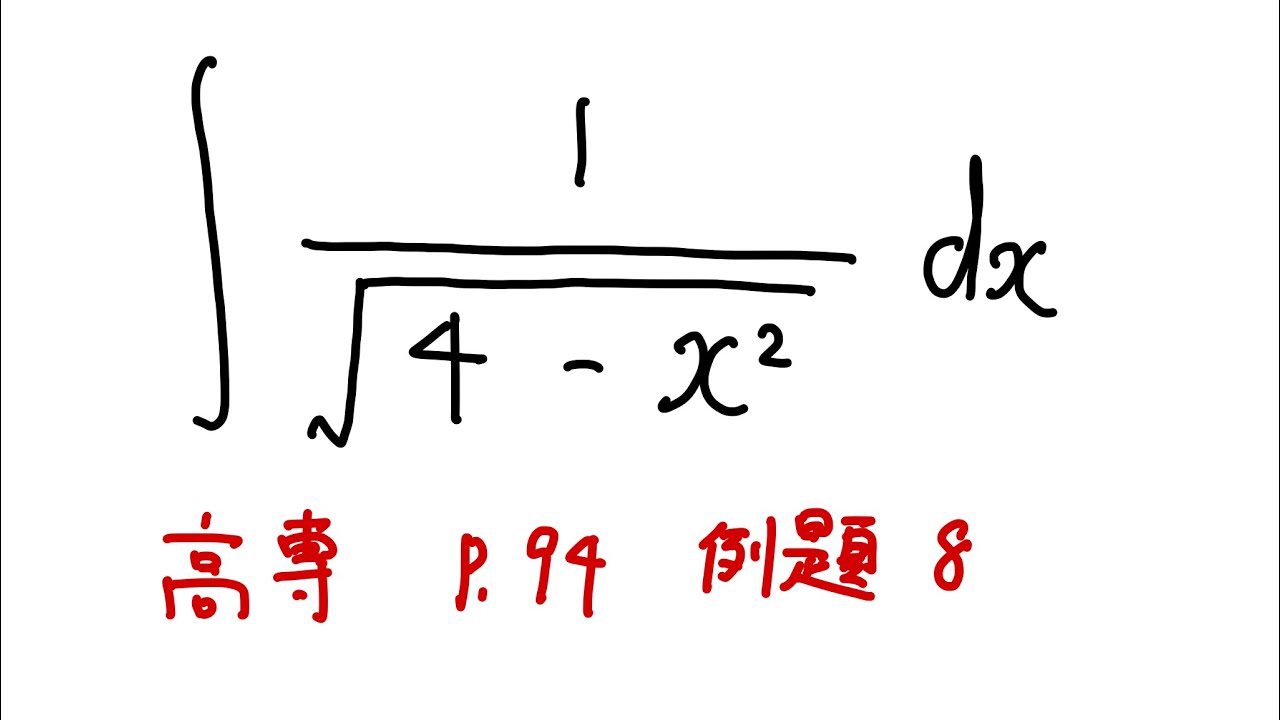
単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
下記の不定積分を解け。
$\displaystyle \int \displaystyle \frac{1}{\sqrt{ 4-x^2 }} dx$
この動画を見る
下記の不定積分を解け。
$\displaystyle \int \displaystyle \frac{1}{\sqrt{ 4-x^2 }} dx$
#千葉大学2016#定積分#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \cos^3x$ $dx$
出典:2016年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \cos^3x$ $dx$
出典:2016年千葉大学
#高専_8#不定積分#元高専教員
単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
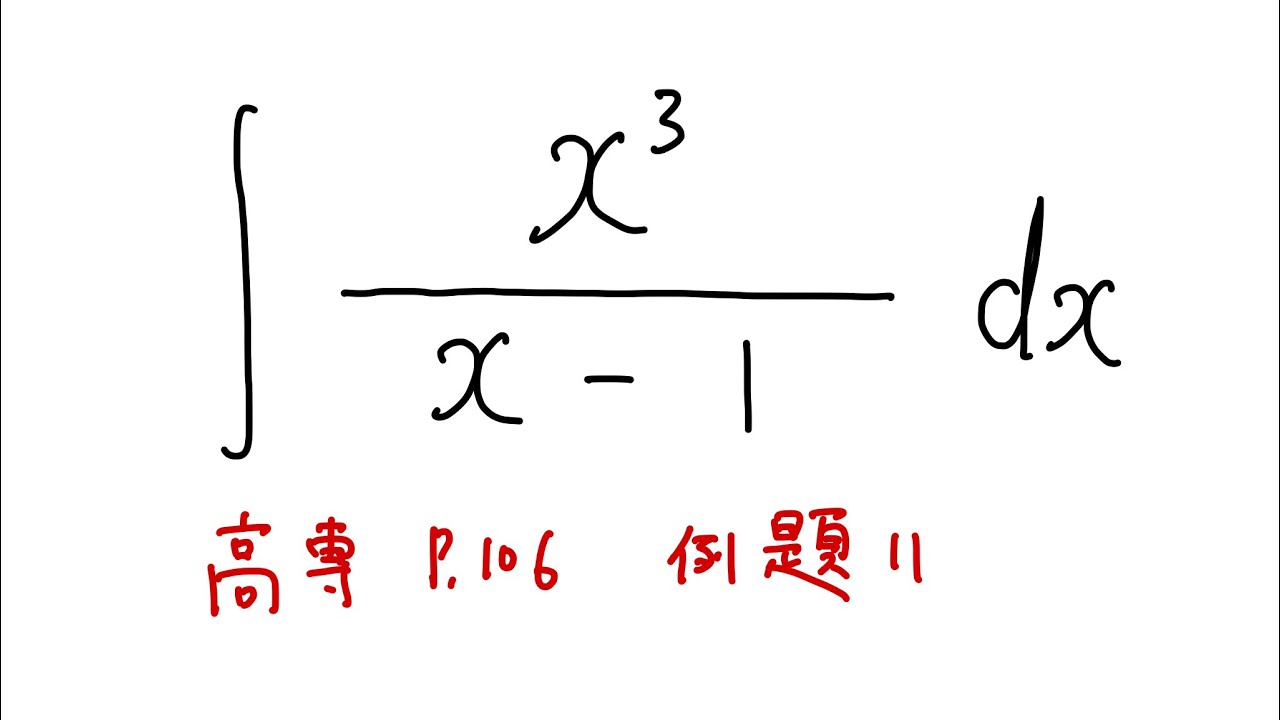
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{x^3}{x-1}$ $dx$
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{x^3}{x-1}$ $dx$
#千葉大学2021#不定積分#元高専教員
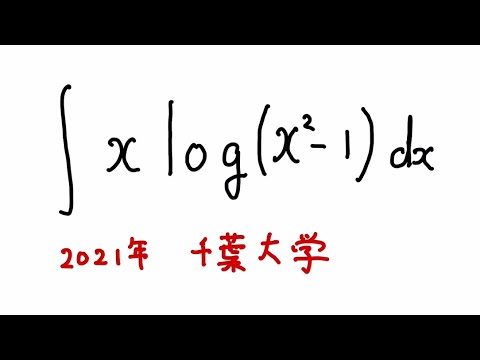
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int x log(x^2-1) dx$
出典:2021年千葉大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int x log(x^2-1) dx$
出典:2021年千葉大学
#高専_7#定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\sqrt{ 2 }} \displaystyle \frac{1+2x}{\sqrt{ 4-x^2 }} dx$
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\sqrt{ 2 }} \displaystyle \frac{1+2x}{\sqrt{ 4-x^2 }} dx$
#千葉大学2018#不定積分#数学者
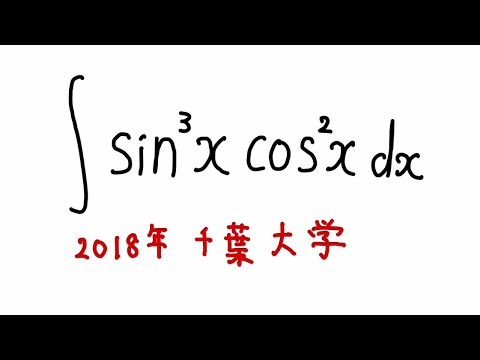
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int \sin^3x \cos^2x$ $dx$
出典:2018年千葉大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \sin^3x \cos^2x$ $dx$
出典:2018年千葉大学
#高専_6#不定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int (3x+1)\cos2x$ $dx$
この動画を見る
以下の不定積分を解け。
$\displaystyle \int (3x+1)\cos2x$ $dx$
#高専数学_5#不定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
下記の不定積分を解け。
$\displaystyle \int x log (x+1)$ $dx$
この動画を見る
下記の不定積分を解け。
$\displaystyle \int x log (x+1)$ $dx$
#千葉大学2020#不定積分#ますただ
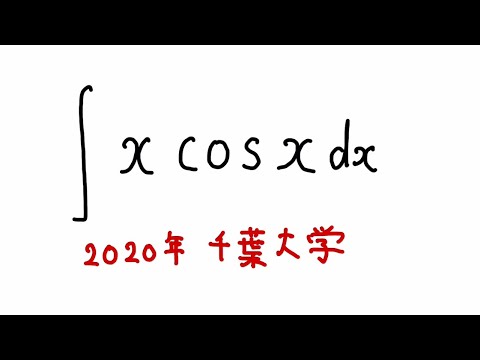
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x\cos x$ $dx$
出典:2024年千葉大学
この動画を見る
$\displaystyle \int x\cos x$ $dx$
出典:2024年千葉大学
#高専_4#不定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{(log t)^2}{t} dt$
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \displaystyle \frac{(log t)^2}{t} dt$
#高専_3#定積分#元高専教員

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} (e^x-e^{-x})^2(e^x+e^{-x}) dx$
この動画を見る
$\displaystyle \int_{-1}^{1} (e^x-e^{-x})^2(e^x+e^{-x}) dx$
#高専_2#定積分

単元:
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (1-\sin^3x)\cos x$ $dx$
この動画を見る
$\displaystyle \int (1-\sin^3x)\cos x$ $dx$
#高専#不定積分-1

単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 4-x^2 }} dx$
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ 4-x^2 }} dx$
#千葉大学2024#定積分
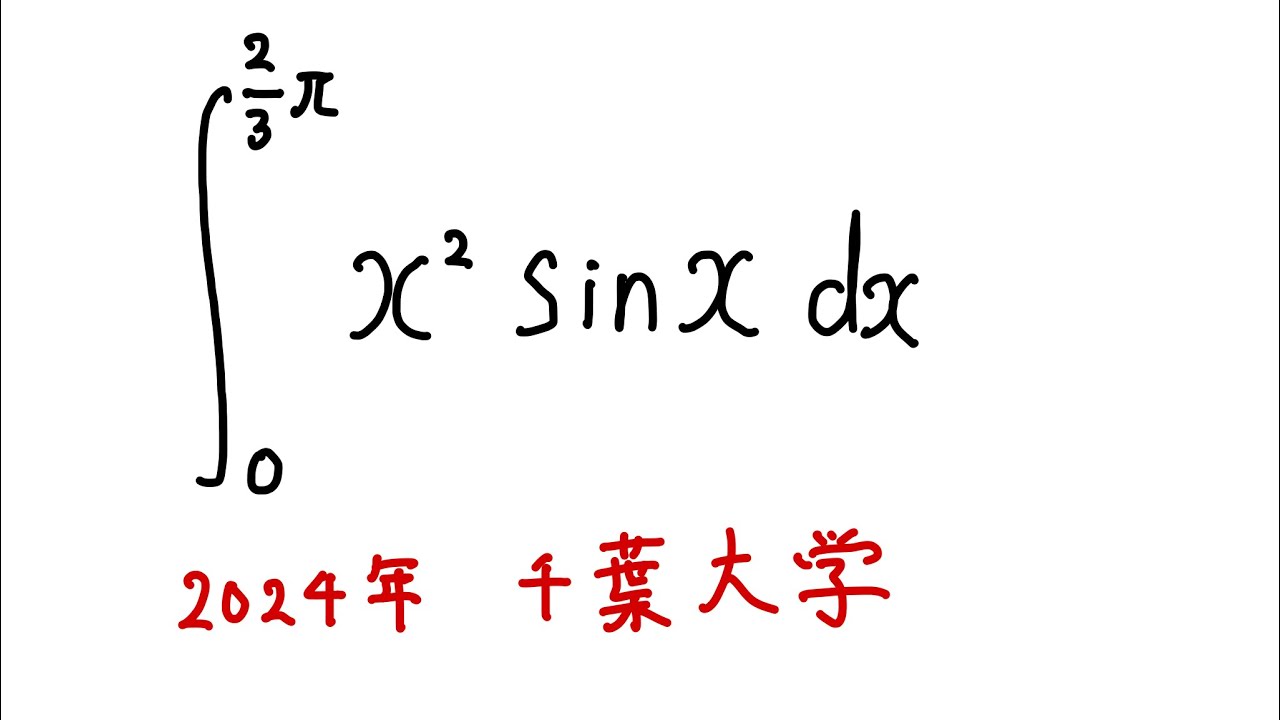
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x^2\sin x$ $dx$
出典:2024年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x^2\sin x$ $dx$
出典:2024年千葉大学
#千葉大学2023#定積分#ますただ
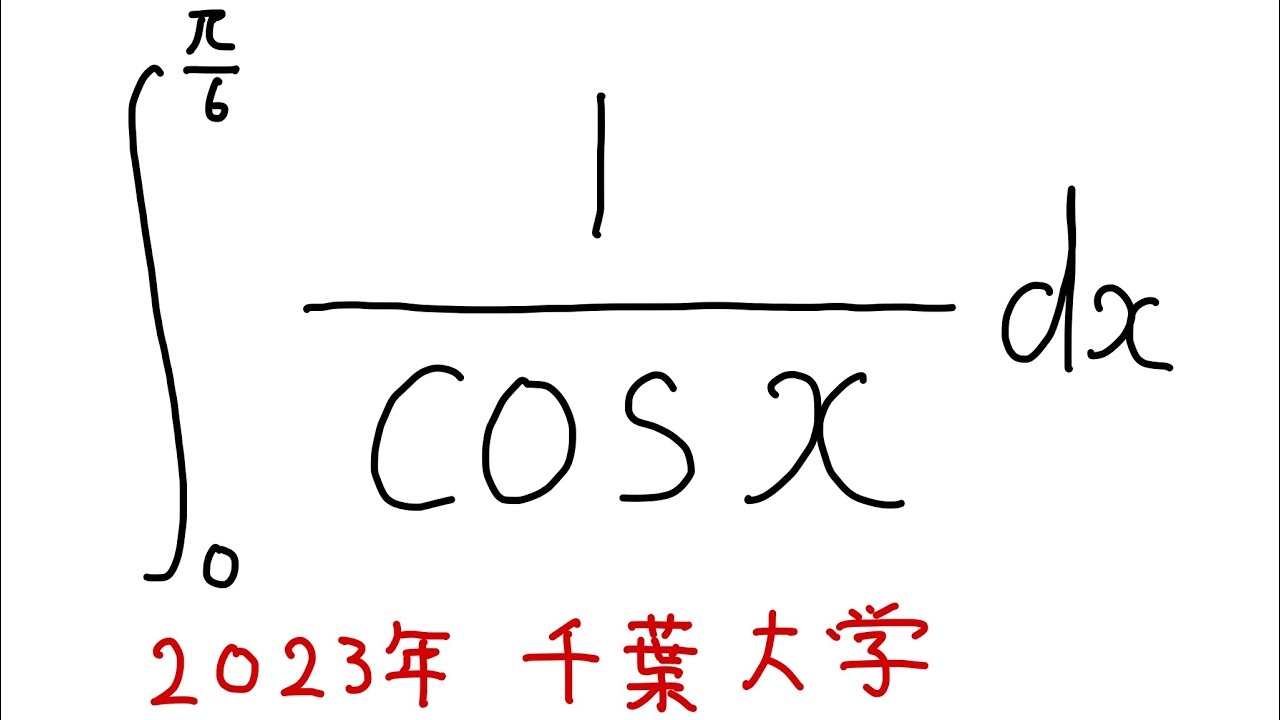
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{1}{\cos x} dx$
出典:2023年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{1}{\cos x} dx$
出典:2023年千葉大学
#千葉大学2023#定積分
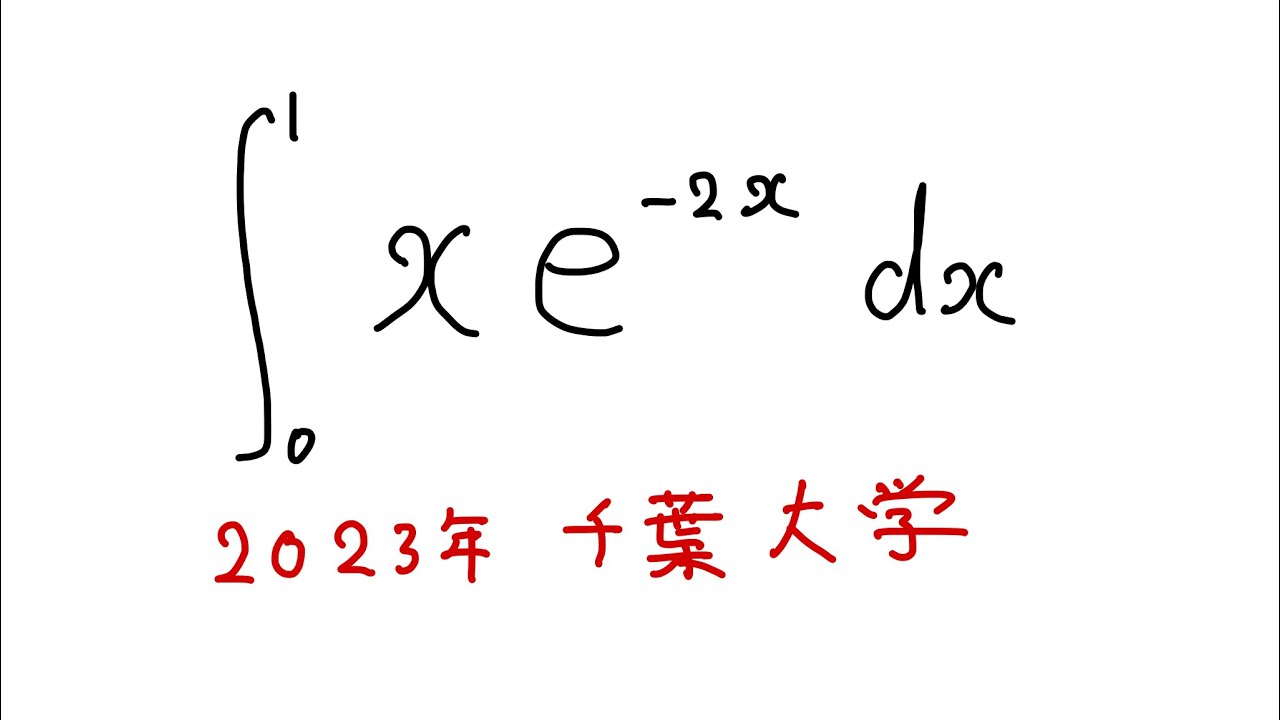
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
この動画を見る
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
#広島市立大学#不定積分#ますただ
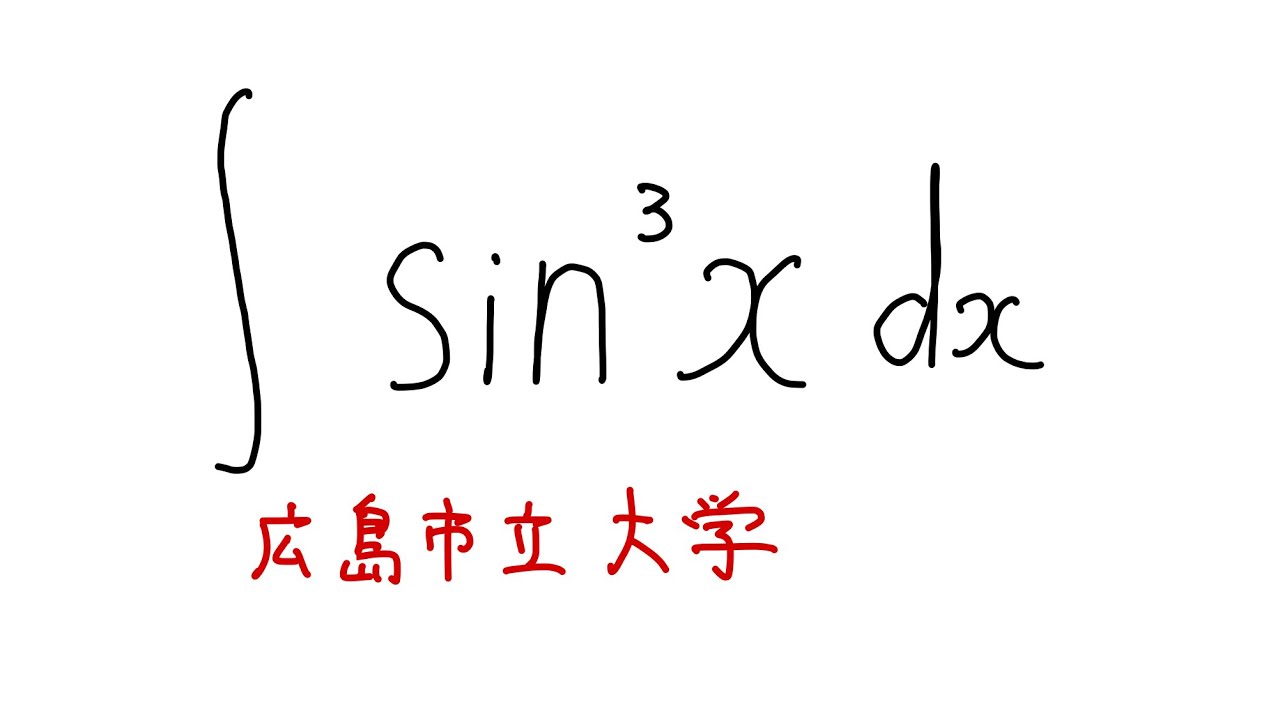
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sin^3 x$ $dx$
広島市立大過去問
この動画を見る
$\displaystyle \int \sin^3 x$ $dx$
広島市立大過去問
福田の数学〜筑波大学2024理系第4問〜媒介変数表示で表された曲線のグラフと面積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標平面において、媒介変数表示$x=-t(t-\dfrac32), y=\sin\pi t ~~ (0\leqq t \leqq 1)$で表される曲線を$C$とする。以下の問いに答えよ
(1) 定積分$\displaystyle \int_0^1 t\sin\pi t dt$を求めよ。
(2) 実数$a$に対し、曲線$C$と直線$x=a$の共有点の個数を求めよ。
(3) 曲線$C$と$x$軸で囲まれた図形の面積を求めよ。
この動画を見る
座標平面において、媒介変数表示$x=-t(t-\dfrac32), y=\sin\pi t ~~ (0\leqq t \leqq 1)$で表される曲線を$C$とする。以下の問いに答えよ
(1) 定積分$\displaystyle \int_0^1 t\sin\pi t dt$を求めよ。
(2) 実数$a$に対し、曲線$C$と直線$x=a$の共有点の個数を求めよ。
(3) 曲線$C$と$x$軸で囲まれた図形の面積を求めよ。
#富山大学推薦2019#定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{x}{x^2+1} dx$
出典:2019年富山大学推薦
この動画を見る
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{x}{x^2+1} dx$
出典:2019年富山大学推薦
#広島市立大学2014#不定積分#ますただ
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
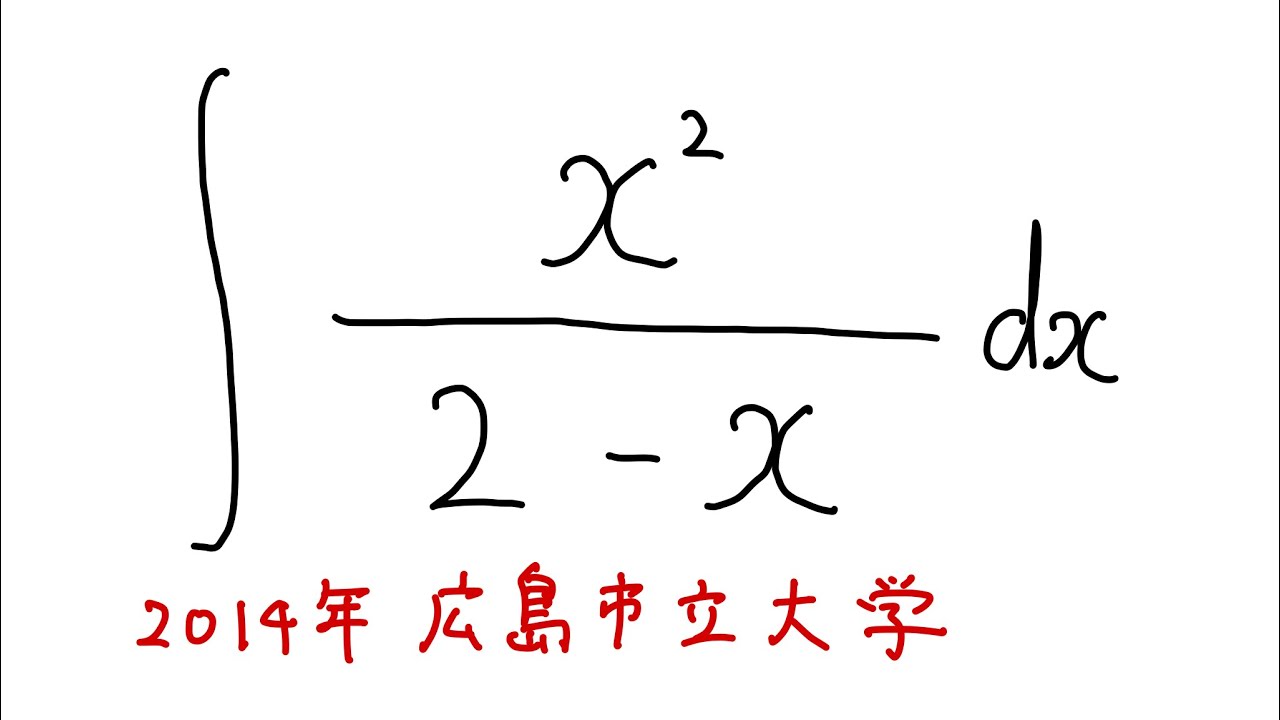
$\displaystyle \int \displaystyle \frac{x^2}{2-x} dx$
出典:2014年広島市立大学
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2}{2-x} dx$
出典:2014年広島市立大学
#電気通信大学2015#定積分#ますただ
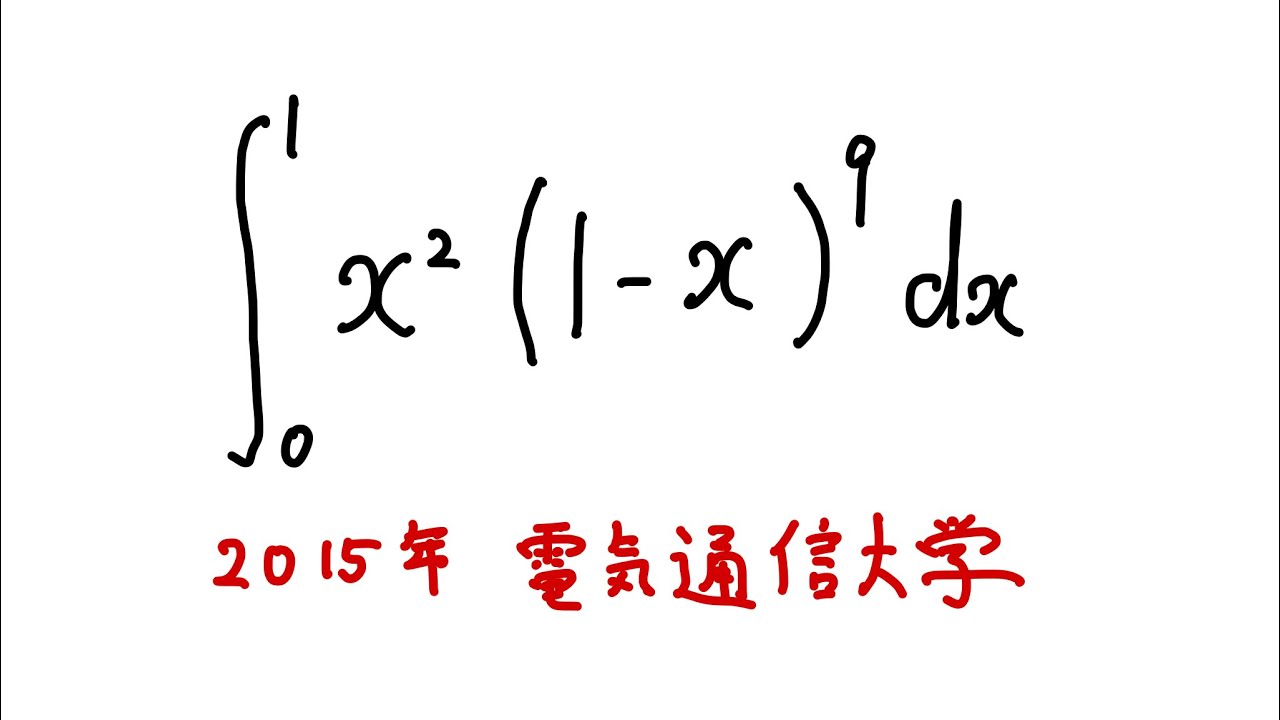
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典:2015年電気通信大学
この動画を見る
$\displaystyle \int_{0}^{1} x^2(1-x)^9 dx$
出典:2015年電気通信大学
#富山大学薬学部2018#不定積分
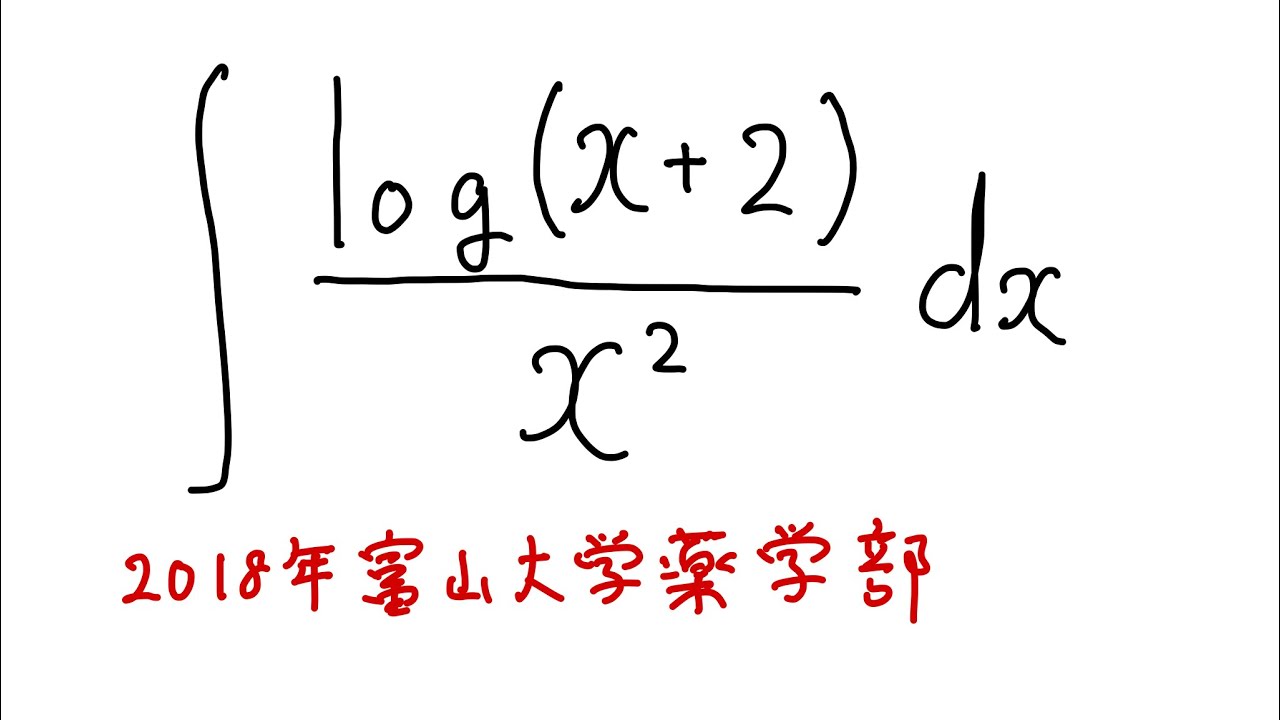
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{log(x+2)}{x^2} dx$
出典:2018年富山大学薬学部
この動画を見る
$\displaystyle \int \displaystyle \frac{log(x+2)}{x^2} dx$
出典:2018年富山大学薬学部
#数検準1級1次_4#不定積分
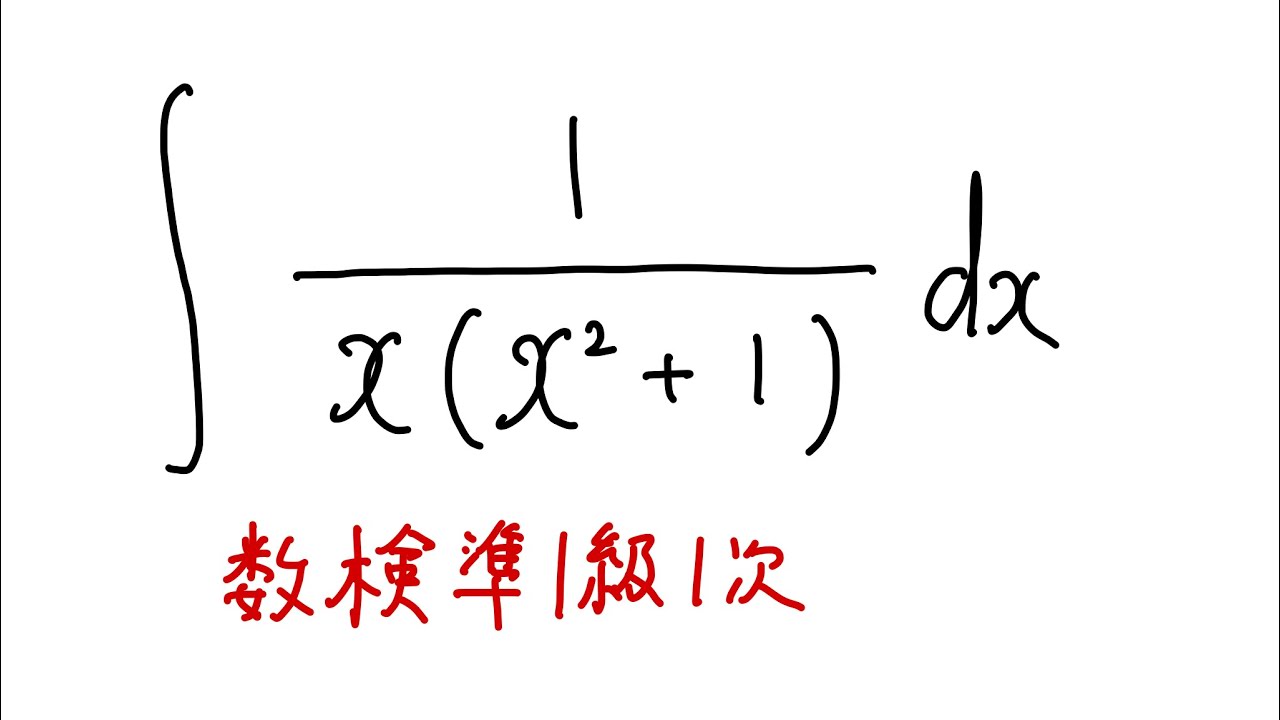
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{x(x^2+1)} dx$
出典:数検準1級1次
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{x(x^2+1)} dx$
出典:数検準1級1次
#藤田医科大学2023#定積分
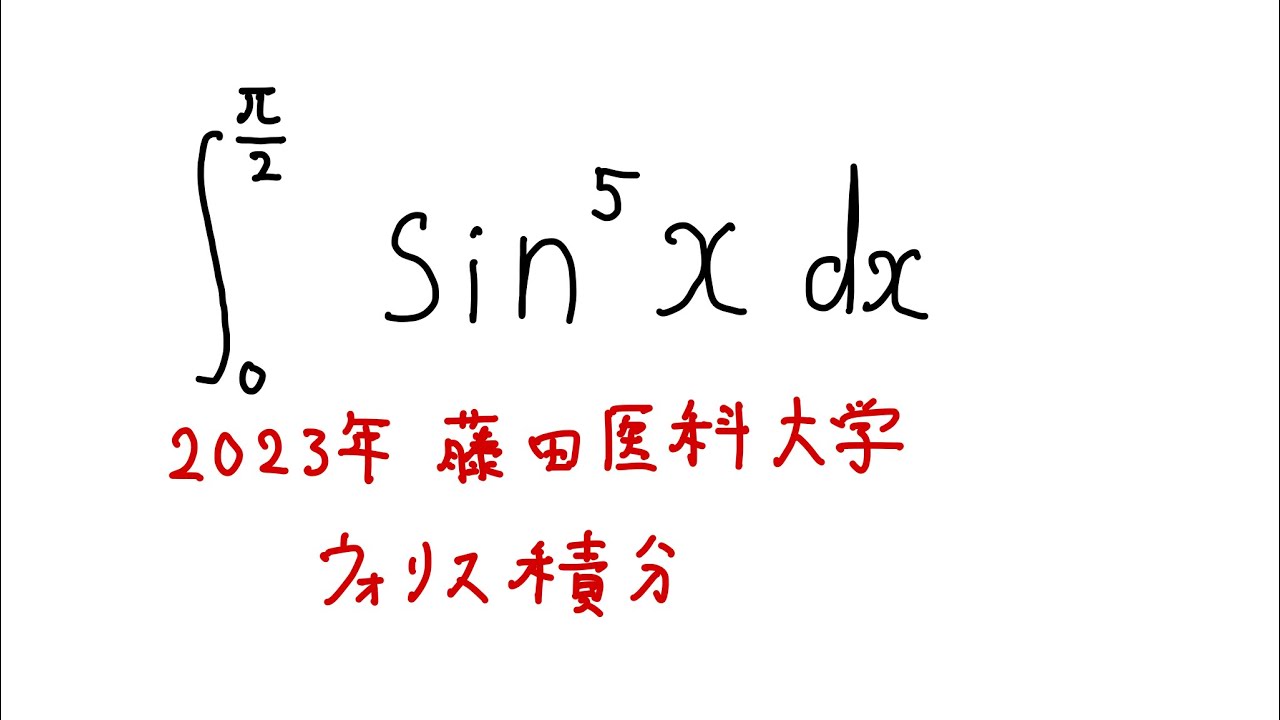
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#藤田医科大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^5x$ $dx$
出典:2023年藤田医科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^5x$ $dx$
出典:2023年藤田医科大学
