複素数平面
複素数平面
東京工業大学 三次方程式 Japanese university entrance exam questions
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
東京工業大学'72過去問題
$x^3-x+k=0(k>0)$
絶対値が1の虚根をもつ。
3つの根を求めよ。
この動画を見る
東京工業大学'72過去問題
$x^3-x+k=0(k>0)$
絶対値が1の虚根をもつ。
3つの根を求めよ。
福田の一夜漬け数学〜複素数平面(1)〜極形式と回転
単元：
#複素数平面#複素数平面#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
(練習)以下の式を極形式表示に直せ。ただし$0 \leqq \theta\leqq 2\pi$とする。
(1)$2-2i$
(2)$(2-2\sqrt3i)(i-1)$
$\alpha=1+i,\beta=3+2i$のとき、この2点を一辺とする正三角形の
残りの頂点を表す複素数を求めよ。
この動画を見る
(練習)以下の式を極形式表示に直せ。ただし$0 \leqq \theta\leqq 2\pi$とする。
(1)$2-2i$
(2)$(2-2\sqrt3i)(i-1)$
$\alpha=1+i,\beta=3+2i$のとき、この2点を一辺とする正三角形の
残りの頂点を表す複素数を求めよ。
ド・モアブルの定理を用いてオイラーの公式を導く
単元：
#複素数平面#関数と極限#複素数平面#関数の極限#数学(高校生)#数C#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
ド・モアブルの定理を用いてオイラーの公式を導く方法を解説していきます.
この動画を見る
ド・モアブルの定理を用いてオイラーの公式を導く方法を解説していきます.
なぜ、マイナス×マイナスはプラスなのか？ 負✕負＝正 虚数（複素数）を使って説明します
中学生の知識でオイラーの公式を理解しよう Vol 8 複素数 ドゥモアブルの定理
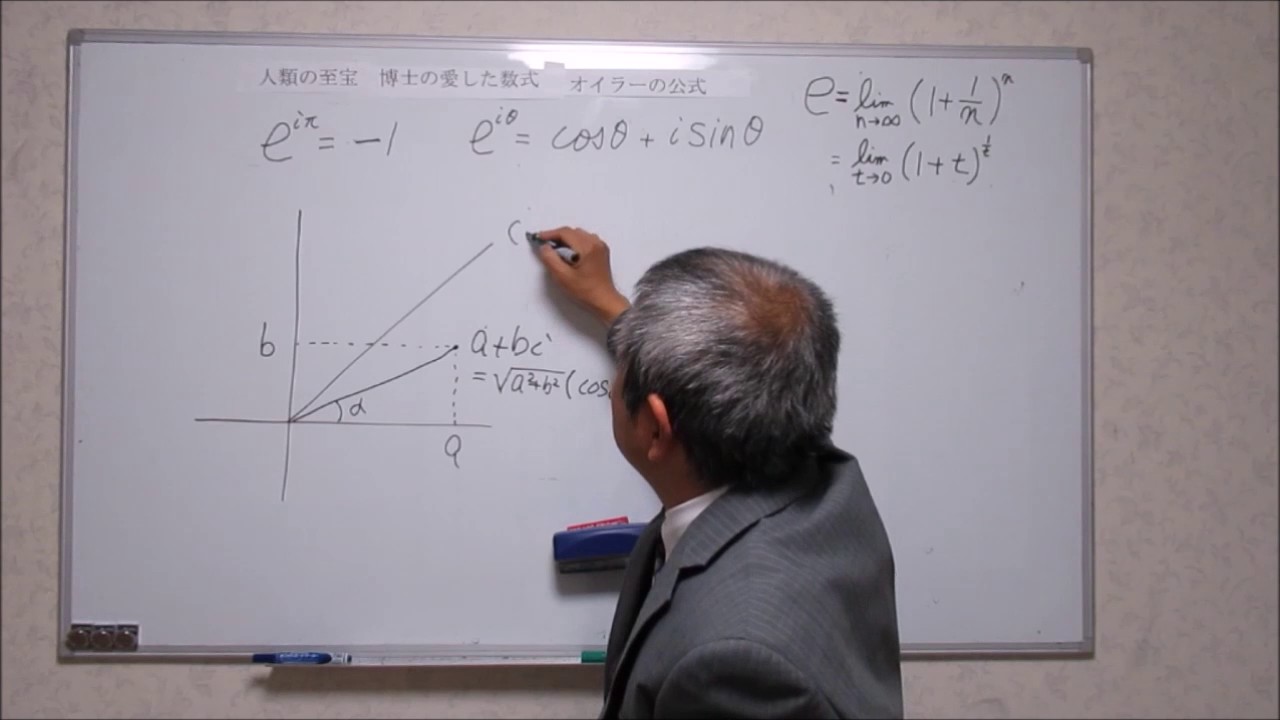
Euler's formula 中学生の知識でオイラーの公式を理解しよう 最終回
中学生の知識でオイラーの公式を理解しよう Vol 9
中学生の知識でオイラーの公式を理解しよう Vol 7 弧度法 sinの微分
単元：
#複素数平面#微分とその応用#複素数平面#色々な関数の導関数#数学(高校生)#数C#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
中学生の知識でオイラーの公式に関して解説していきます. Vol 7 弧度法
この動画を見る
中学生の知識でオイラーの公式に関して解説していきます. Vol 7 弧度法
【高校数学】数Ⅲ－２０ 三角形の形状①
単元：
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#数C
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
複素数平面上の原点$O$と異なる2点$A,B$の表す複素数を
それぞれ$\alpha,\beta$とする.
等式$\alpha ^ 2 - \alpha\beta + \beta ^ 2 = 0$が成り立つとき,
次の問いに答えよ.
①複素数$\dfrac{\beta}{\alpha}$を求めよ.
②$△OAB$はどのような三角形か.
この動画を見る
複素数平面上の原点$O$と異なる2点$A,B$の表す複素数を
それぞれ$\alpha,\beta$とする.
等式$\alpha ^ 2 - \alpha\beta + \beta ^ 2 = 0$が成り立つとき,
次の問いに答えよ.
①複素数$\dfrac{\beta}{\alpha}$を求めよ.
②$△OAB$はどのような三角形か.
【高校数学】数Ⅲ－１８ 複素数と三角形①
単元：
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#数C
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
複素数$\sqrt3+i,4i$が表す点をそれぞれ$P,Q$とする.
このとき,半直線$PQ$が実軸の正の向きよなす角を求めよ.
この動画を見る
複素数$\sqrt3+i,4i$が表す点をそれぞれ$P,Q$とする.
このとき,半直線$PQ$が実軸の正の向きよなす角を求めよ.
【高校数学】数Ⅲ－１５ 円と分点①
単元：
#複素数平面#複素数平面#数学(高校生)#数C
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
2つの複素数$\alpha=2+4i, \beta = 7 -i$を表す複素数平面上の点を
それぞれ$A,B$とする.
線分$AB$について,次の点を表す複素数を求めよう.
①$3:2$に内分する点
②$2:3$に外分する点
③中点
この動画を見る
2つの複素数$\alpha=2+4i, \beta = 7 -i$を表す複素数平面上の点を
それぞれ$A,B$とする.
線分$AB$について,次の点を表す複素数を求めよう.
①$3:2$に内分する点
②$2:3$に外分する点
③中点
【高校数学】数Ⅲ－１１ 複素数の積の図表示③
単元：
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#数C
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①$z_1=\sqrt3+i,z_2=2+2i$のとき,積$z_1z_2$を図示せよ.
②$\dfrac{1+\sqrt3i}{1+i}$を複素数平面上に図示しよう.
この動画を見る
①$z_1=\sqrt3+i,z_2=2+2i$のとき,積$z_1z_2$を図示せよ.
②$\dfrac{1+\sqrt3i}{1+i}$を複素数平面上に図示しよう.
【高校数学】数Ⅲ－２ 複素数平面・共役な複素数②
単元：
#複素数平面#複素数平面#数学(高校生)#数C
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
複素数$z$が,$2z-5\overline{z}=-9+14i$を満たすとき,
共役複素数の性質を利用して$z$を求めよ.
この動画を見る
複素数$z$が,$2z-5\overline{z}=-9+14i$を満たすとき,
共役複素数の性質を利用して$z$を求めよ.
【高校数学】数Ⅲ－１ 複素数平面・共役な複素数①
単元：
#複素数平面#複素数平面#数学(高校生)#数C
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$z=1+2i$とする.
複素平面上に次の点を図示しよう.
⑤$A(Z)$
⑥$B(-Z)$
⑦$C(\overline{ Z})$
⑧$D(-\overline{Z})$
図は動画内参照
この動画を見る
$z=1+2i$とする.
複素平面上に次の点を図示しよう.
⑤$A(Z)$
⑥$B(-Z)$
⑦$C(\overline{ Z})$
⑧$D(-\overline{Z})$
図は動画内参照