 媒介変数表示と極座標
媒介変数表示と極座標
 媒介変数表示と極座標
媒介変数表示と極座標
高専数学 微積I #234(1)(2) 極座標表示の曲線の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
(1)曲線$r=\theta^2\left(0\leqq \theta \leqq \dfrac{\theta}{2}\right)$と
半直線$\theta=\dfrac{\theta}{2}$で囲まれた図形の面積を求めよ.
(2)曲線$r=\cos\theta+2(0\leqq \theta \leqq 2\pi)$で囲まれた
図形の面積を求めよ.
この動画を見る
(1)曲線$r=\theta^2\left(0\leqq \theta \leqq \dfrac{\theta}{2}\right)$と
半直線$\theta=\dfrac{\theta}{2}$で囲まれた図形の面積を求めよ.
(2)曲線$r=\cos\theta+2(0\leqq \theta \leqq 2\pi)$で囲まれた
図形の面積を求めよ.
高専数学 微積I #229(2) 媒介変数表示関数のx軸回転体の体積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \dfrac{\pi}{2}$である.
$x=\sin t$
$y=\sin 2t$
と$x$軸で囲まれた図形を$x$軸のまわりに回転して
できる回転体の体積$V$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{2}$である.
$x=\sin t$
$y=\sin 2t$
と$x$軸で囲まれた図形を$x$軸のまわりに回転して
できる回転体の体積$V$を求めよ.
高専数学 微積I #229(1) 媒介変数表示関数のx軸回転体の体積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq 1$とする.
$x=\sqrt t$
$y=\sqrt t-t$
と$x$軸で囲まれた図形を
$x$軸のまわりに回転してできる回転体の
体積$V$を求めよ.
この動画を見る
$0\leqq t\leqq 1$とする.
$x=\sqrt t$
$y=\sqrt t-t$
と$x$軸で囲まれた図形を
$x$軸のまわりに回転してできる回転体の
体積$V$を求めよ.
高専数学 微積I #227(3) 媒介変数表示関数の曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \pi$とする.
$x=\cos t+ \cos 2t$
$y=2\sin t- \sin 2t$
の曲線の長さ$L$を求めよ.
この動画を見る
$0\leqq t\leqq \pi$とする.
$x=\cos t+ \cos 2t$
$y=2\sin t- \sin 2t$
の曲線の長さ$L$を求めよ.
高専数学 微積I #227(2) 媒介変数表示関数の曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \pi$とする.
$x=\cos t+t \sin t$
$y=\sin t-t \cos t$
の曲線の長さ$L$を求めよ.
この動画を見る
$0\leqq t\leqq \pi$とする.
$x=\cos t+t \sin t$
$y=\sin t-t \cos t$
の曲線の長さ$L$を求めよ.
高専数学 微積I #227(1) 媒介変数表示の曲線の長さ

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t \leqq \sqrt3$である.
$x=3t^2,y=3t-t^3$の曲線の長さ$L$を求めよ.
この動画を見る
$0\leqq t \leqq \sqrt3$である.
$x=3t^2,y=3t-t^3$の曲線の長さ$L$を求めよ.
高専数学 微積I #226(3) 媒介変数表示の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \dfrac{\pi}{2}$
曲線$x=\cos t,\cos 2t+1$
$x$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{2}$
曲線$x=\cos t,\cos 2t+1$
$x$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
高専数学 微積I #226(2) 媒介変数表示の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq \dfrac{\pi}{4}$とする.
曲線$x=\tan t,y=\sin t+1$と
$x$軸,$y$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{4}$とする.
曲線$x=\tan t,y=\sin t+1$と
$x$軸,$y$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
高専数学 微積I #226(1) 媒介変数表示の面積

単元:
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$0\leqq t\leqq 1$とする.
曲線$x=t^2,y=t^2-2t+1$
$x$軸,$y$軸で囲まれた図形の
面積$S$を求めよ.
この動画を見る
$0\leqq t\leqq 1$とする.
曲線$x=t^2,y=t^2-2t+1$
$x$軸,$y$軸で囲まれた図形の
面積$S$を求めよ.
福田の数学〜早稲田大学2021年社会科学部第1問〜三角関数で表された点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#三角関数#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ a,bを定数とし、関数$f(x)=x^2+ax+b$ とする。方程式$f(x)=0$の2つの解$\alpha,\beta\\$
が次式で与えられている。
$\alpha=\frac{\sin\theta}{1+\cos\theta}$, $\beta=\frac{\sin\theta}{1-\cos\theta}\\$
ここで$\theta$は、$0 \lt \theta \lt \pi$の定数である。次の問いに答えよ。
$(1)a,b$を$\theta$を用いて表せ。
$(2)\theta$が$0$ $\lt \theta \pi$で変化するとき、放物線$y=f(x)$の頂点の軌跡を求めよ。
$(3)\int_0^{2\sin\theta}f(x)dx=0$ となる$\theta$の値を全て求めよ。
2021早稲田大学社会科学部過去問
この動画を見る
${\Large\boxed{1}}$ a,bを定数とし、関数$f(x)=x^2+ax+b$ とする。方程式$f(x)=0$の2つの解$\alpha,\beta\\$
が次式で与えられている。
$\alpha=\frac{\sin\theta}{1+\cos\theta}$, $\beta=\frac{\sin\theta}{1-\cos\theta}\\$
ここで$\theta$は、$0 \lt \theta \lt \pi$の定数である。次の問いに答えよ。
$(1)a,b$を$\theta$を用いて表せ。
$(2)\theta$が$0$ $\lt \theta \pi$で変化するとき、放物線$y=f(x)$の頂点の軌跡を求めよ。
$(3)\int_0^{2\sin\theta}f(x)dx=0$ となる$\theta$の値を全て求めよ。
2021早稲田大学社会科学部過去問
18岡山県教員使用試験(数学:5番 媒介変数表示のグラフ・面積)

単元:
#平面上の曲線#その他#媒介変数表示と極座標#数学(高校生)#数C#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$ $ 0\leqq t\leqq \pi$,
$x=\cos t,y=\sin 2t+2\sin t$とする.
(1)曲線の概形
(2)曲線とx軸で囲まれた面積を求めよ.
この動画を見る
$\boxed{5}$ $ 0\leqq t\leqq \pi$,
$x=\cos t,y=\sin 2t+2\sin t$とする.
(1)曲線の概形
(2)曲線とx軸で囲まれた面積を求めよ.
数検準1級1次過去問【2020年12月】5番:極方程式

単元:
#数学検定・数学甲子園・数学オリンピック等#平面上の曲線#媒介変数表示と極座標#数学検定#数学検定準1級#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
5⃣ 極方程式
r=4sinθ+6cosθ
で表される図形を求めよ。
この動画を見る
5⃣ 極方程式
r=4sinθ+6cosθ
で表される図形を求めよ。
重積分⑦-2【極座標による変数変換】(高専数学 微積II,数検1級1次解析対応)

単元:
#大学入試過去問(数学)#数学検定・数学甲子園・数学オリンピック等#平面上の曲線#積分とその応用#2次曲線#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#数学検定#数学検定1級#数学(高校生)#数C#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
$x^2+y^2+z^2=4a^2$ , $z \geqq 0$
$(x-a)^2+y^2=a^2$ , $z \geqq 0$
xy平面 (a>0)で囲まれた体積Vを求めよ。
この動画を見る
$x^2+y^2+z^2=4a^2$ , $z \geqq 0$
$(x-a)^2+y^2=a^2$ , $z \geqq 0$
xy平面 (a>0)で囲まれた体積Vを求めよ。
東大 座標上の鋭角三角形

単元:
#数A#図形の性質#平面上の曲線#三角形の辺の比(内分・外分・二等分線)#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a,b$は実数であり,$b\neq 0$である.
$O(0,0).P(1,0),Q(a,b)$
(1)$\triangle OPQ$が鋭角三角形になる$a,b$の条件を不等式で表せ.
(2)$m,n$整数,$a,b$は(1)の条件を満たすとき,$(m+na)^2-(m+na)+n^2b^2 \geqq 0$を示せ.
1998東大過去問
この動画を見る
$a,b$は実数であり,$b\neq 0$である.
$O(0,0).P(1,0),Q(a,b)$
(1)$\triangle OPQ$が鋭角三角形になる$a,b$の条件を不等式で表せ.
(2)$m,n$整数,$a,b$は(1)の条件を満たすとき,$(m+na)^2-(m+na)+n^2b^2 \geqq 0$を示せ.
1998東大過去問
群馬大 複素数 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#平面上の曲線#複素数#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#数学(高校生)#群馬大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$z=\displaystyle \frac{\sqrt{ 3 }-1}{2}+\displaystyle \frac{\sqrt{ 3 }+1}{2}i$
(1)
$\displaystyle \frac{z}{1+i}$を$a+bi$の形で表せ
(2)
$z$を極形式で表せ
(3)
$z^{12}$を求めよ
出典:2004年国立大学法人群馬大学 過去問
この動画を見る
$z=\displaystyle \frac{\sqrt{ 3 }-1}{2}+\displaystyle \frac{\sqrt{ 3 }+1}{2}i$
(1)
$\displaystyle \frac{z}{1+i}$を$a+bi$の形で表せ
(2)
$z$を極形式で表せ
(3)
$z^{12}$を求めよ
出典:2004年国立大学法人群馬大学 過去問
福田の一夜漬け数学〜図形と方程式〜軌跡(3)媒介変数表示の点、高校2年生

単元:
#数Ⅱ#平面上の曲線#図形と方程式#軌跡と領域#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ 次の媒介変数表示で表された点$P(x,y)$の軌跡を求めよ。
(1)$x=\displaystyle \frac{\cos\theta+\sin\theta}{\sqrt2},$ $y=\displaystyle \frac{\cos\theta-\sin\theta}{\sqrt2}$ ($\theta$は任意の実数)
(2)$x=\displaystyle \frac{1-t^2}{1+t^2},$ $y=\displaystyle \frac{2t}{1+t^2}$ ($t$は任意の実数)
この動画を見る
${\Large\boxed{1}}$ 次の媒介変数表示で表された点$P(x,y)$の軌跡を求めよ。
(1)$x=\displaystyle \frac{\cos\theta+\sin\theta}{\sqrt2},$ $y=\displaystyle \frac{\cos\theta-\sin\theta}{\sqrt2}$ ($\theta$は任意の実数)
(2)$x=\displaystyle \frac{1-t^2}{1+t^2},$ $y=\displaystyle \frac{2t}{1+t^2}$ ($t$は任意の実数)
【高校数学】数Ⅲ-111 接線と法線④(媒介変数表示編)

単元:
#平面上の曲線#微分とその応用#接線と法線・平均値の定理#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の媒介変数で表された曲線において、
()内に示された曲線上の点における接線の方程式を求めよ。
①$\begin{eqnarray}
\left\{
\begin{array}{l}
x=2\cos\theta \\
y=\sin\theta
\end{array}
\right.
\end{eqnarray}$$\quad \left(\theta=\dfrac{\pi}{3}\right)$
②①$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\cos^3 \theta \\
y=\sin^3 \theta
\end{array}
\right.
\end{eqnarray}$$\quad \left(\theta=\dfrac{\pi}{4}\right)$
この動画を見る
次の媒介変数で表された曲線において、
()内に示された曲線上の点における接線の方程式を求めよ。
①$\begin{eqnarray}
\left\{
\begin{array}{l}
x=2\cos\theta \\
y=\sin\theta
\end{array}
\right.
\end{eqnarray}$$\quad \left(\theta=\dfrac{\pi}{3}\right)$
②①$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\cos^3 \theta \\
y=\sin^3 \theta
\end{array}
\right.
\end{eqnarray}$$\quad \left(\theta=\dfrac{\pi}{4}\right)$
【高校数学】数Ⅲ-106 媒介変数表示された関数の導関数

単元:
#平面上の曲線#微分とその応用#色々な関数の導関数#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$x$と$y$の関係が次の式で与えられるとき、
$\dfrac{dy}{dx}$を$t$で表せ。
①$x=\dfrac{1}{1+t^2},y=\dfrac{t}{1+t^2}$
②$x=a(t-\sin t),y=(1-\cos t)\quad (a\gt 0)$
この動画を見る
$x$と$y$の関係が次の式で与えられるとき、
$\dfrac{dy}{dx}$を$t$で表せ。
①$x=\dfrac{1}{1+t^2},y=\dfrac{t}{1+t^2}$
②$x=a(t-\sin t),y=(1-\cos t)\quad (a\gt 0)$
福田の一夜漬け数学〜積分・面積と体積、媒介変数表示(1)〜受験編
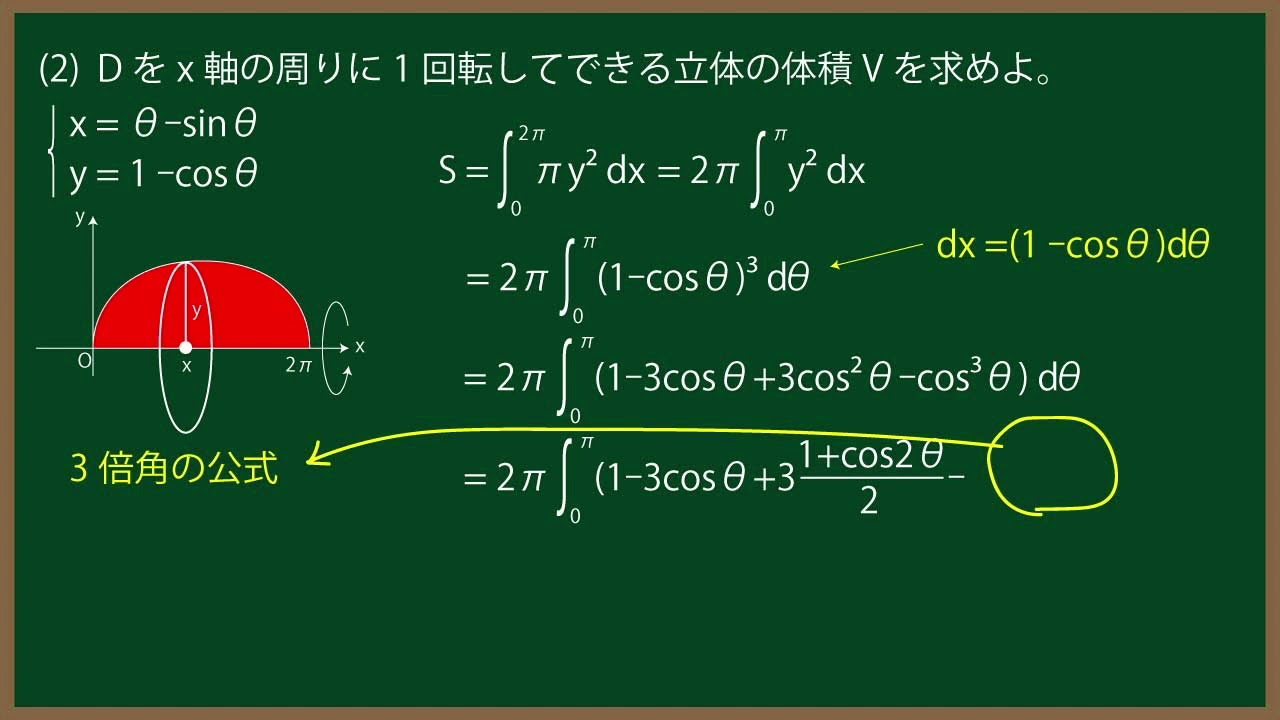
単元:
#平面上の曲線#積分とその応用#定積分#面積・体積・長さ・速度#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\theta-\sin\theta \\
y=1-\cos\theta
\end{array}
\right.
\end{eqnarray}(0 \leqq \theta \leqq 2\pi)$で表される曲線をCとする。
(1)Cとx軸で囲まれる部分の領域をDとする。Dの面積Sを求めよ。
(2)Dをx軸の周りに1回転してできる立体の体積Vを求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=t^2+1 \\
y=2-t-t^2
\end{array}
\right.
\end{eqnarray}(-2 \leqq t \leqq 1)$で表される曲線とx軸で囲まれた面積を求めよ。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\theta-\sin\theta \\
y=1-\cos\theta
\end{array}
\right.
\end{eqnarray}(0 \leqq \theta \leqq 2\pi)$で表される曲線をCとする。
(1)Cとx軸で囲まれる部分の領域をDとする。Dの面積Sを求めよ。
(2)Dをx軸の周りに1回転してできる立体の体積Vを求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=t^2+1 \\
y=2-t-t^2
\end{array}
\right.
\end{eqnarray}(-2 \leqq t \leqq 1)$で表される曲線とx軸で囲まれた面積を求めよ。
【高校数学】数Ⅲ-43 曲線の媒介変数表示④

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$x、y$が$\dfrac{x^2}{2}+\dfrac{y^2}{8}=1$を満たす実数のとき、
$2x^2+xy+y^2$の最大値、最小値を求めよ。
この動画を見る
①$x、y$が$\dfrac{x^2}{2}+\dfrac{y^2}{8}=1$を満たす実数のとき、
$2x^2+xy+y^2$の最大値、最小値を求めよ。
【高校数学】数Ⅲ-42 曲線の媒介変数表示③

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$t$を媒介変数とする。
次の式で表される図形はどのような曲線か。
①$x=\dfrac{1}{1+t^2}、y=\dfrac{t}{1+t^2}$
②$x=t+\dfrac{1}{t}、y=t-\dfrac{1}{t} \quad (t \gt 0)$
この動画を見る
$t$を媒介変数とする。
次の式で表される図形はどのような曲線か。
①$x=\dfrac{1}{1+t^2}、y=\dfrac{t}{1+t^2}$
②$x=t+\dfrac{1}{t}、y=t-\dfrac{1}{t} \quad (t \gt 0)$
【高校数学】数Ⅲ-41 曲線の媒介変数表示②

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
$\theta$を媒介変数とする。次の式で表される図形はどのような曲線か。
①$\begin{eqnarray}
\left\{
\begin{array}{l}
x=3\cos\theta-2 \\
y=5\sin\theta+2
\end{array}
\right.
\end{eqnarray}$
②$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\dfrac{3}{\cos\theta}+5\\
y=2\tan\theta-1
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\theta$を媒介変数とする。次の式で表される図形はどのような曲線か。
①$\begin{eqnarray}
\left\{
\begin{array}{l}
x=3\cos\theta-2 \\
y=5\sin\theta+2
\end{array}
\right.
\end{eqnarray}$
②$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\dfrac{3}{\cos\theta}+5\\
y=2\tan\theta-1
\end{array}
\right.
\end{eqnarray}$
【高校数学】数Ⅲ-40 曲線の媒介変数表示①

単元:
#平面上の曲線#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の曲線を,角$\theta$を媒介変数として表せ.
①$9x^2+y^2=16$
②$x^2+y^2=16$
③$4x^2-9y^2=36$
この動画を見る
次の曲線を,角$\theta$を媒介変数として表せ.
①$9x^2+y^2=16$
②$x^2+y^2=16$
③$4x^2-9y^2=36$
