 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田の数学・入試問題解説〜東北大学2022年理系第5問〜空間内の直線上の点列の極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標空間内において、ベクトル
$\overrightarrow{ a }=(1,2,1), \overrightarrow{ b }=(1,1,-1), \overrightarrow{ c }=(0,0,1)$
が定める直線
$l:s\overrightarrow{ a }, l':t\overrightarrow{ b }+\overrightarrow{ c }$
を考える。点$A_1$を原点(0,0,0)とし、点$A_1$から直線l'に下ろした垂線$A_1B_1$と
おく。次に、点$B_1(t_1\overrightarrow{ b }+\overrightarrow{ c })$から直線lに下ろした垂線を$B_1A_2$とおく。
同様に、点$A_k(s_k\overrightarrow{ a })$から直線l'に下ろした垂線を$A_kB_k$、点$B_k(t_k\overrightarrow{ b }+\overrightarrow{ c })$から直線l
に下ろした垂線を$B_kA_{k+1}$とする手順を繰り返して、点$A_n(s_n\overrightarrow{ a }),B_n(t_n\overrightarrow{ b }+\overrightarrow{ c })$
(nは正の整数)を定める。
(1)$s_n$を用いて$s_{n+1}$を表せ。
(2)極限値$S=\lim_{n \to \infty}s_n, T=\lim_{n \to \infty}t_n$を求めよ。
(3)(2)で求めたS,Tに対して、点A,Bをそれぞれ$A(S\overrightarrow{ a }),B(T\overrightarrow{ b }+\overrightarrow{ c })$とおくと、
直線ABは2直線l,l'の両方と直交することを示せ。
2022東北大学理系過去問
この動画を見る
座標空間内において、ベクトル
$\overrightarrow{ a }=(1,2,1), \overrightarrow{ b }=(1,1,-1), \overrightarrow{ c }=(0,0,1)$
が定める直線
$l:s\overrightarrow{ a }, l':t\overrightarrow{ b }+\overrightarrow{ c }$
を考える。点$A_1$を原点(0,0,0)とし、点$A_1$から直線l'に下ろした垂線$A_1B_1$と
おく。次に、点$B_1(t_1\overrightarrow{ b }+\overrightarrow{ c })$から直線lに下ろした垂線を$B_1A_2$とおく。
同様に、点$A_k(s_k\overrightarrow{ a })$から直線l'に下ろした垂線を$A_kB_k$、点$B_k(t_k\overrightarrow{ b }+\overrightarrow{ c })$から直線l
に下ろした垂線を$B_kA_{k+1}$とする手順を繰り返して、点$A_n(s_n\overrightarrow{ a }),B_n(t_n\overrightarrow{ b }+\overrightarrow{ c })$
(nは正の整数)を定める。
(1)$s_n$を用いて$s_{n+1}$を表せ。
(2)極限値$S=\lim_{n \to \infty}s_n, T=\lim_{n \to \infty}t_n$を求めよ。
(3)(2)で求めたS,Tに対して、点A,Bをそれぞれ$A(S\overrightarrow{ a }),B(T\overrightarrow{ b }+\overrightarrow{ c })$とおくと、
直線ABは2直線l,l'の両方と直交することを示せ。
2022東北大学理系過去問
大学入試問題#149 岩手大学(2019) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{3}\displaystyle \frac{x}{(4-x)^3}\ dx$を計算せよ。
出典:2019年岩手大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{3}\displaystyle \frac{x}{(4-x)^3}\ dx$を計算せよ。
出典:2019年岩手大学 入試問題
整式の剰余

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^{2022}$を$(x+1)(x^2+1)(x^4+1)(x^8+1)$で割った余りを求めよ.
この動画を見る
$x^{2022}$を$(x+1)(x^2+1)(x^4+1)(x^8+1)$で割った余りを求めよ.
中学生もわかる!と思う!指数の方程式
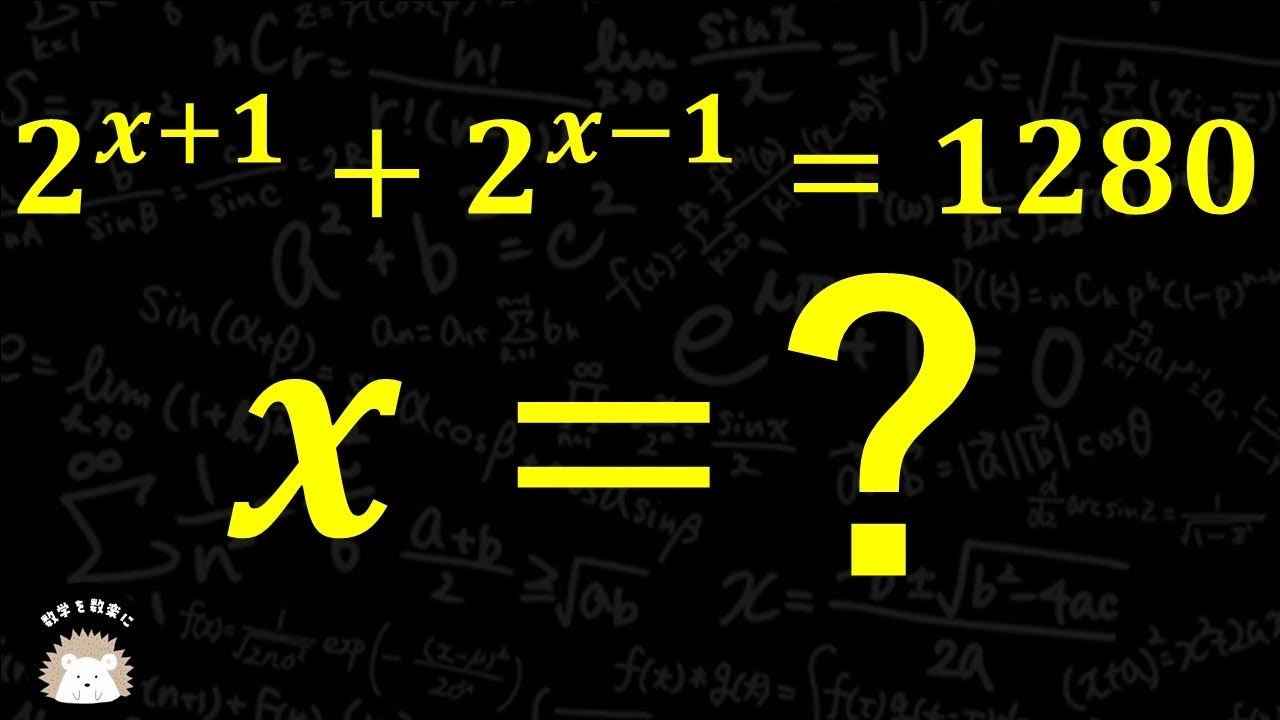
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{x+1}+2^{x-1} = 1280$
x=?
この動画を見る
$2^{x+1}+2^{x-1} = 1280$
x=?
シンガポール数学オリンピックの問題
単元:
#数A#数学検定・数学甲子園・数学オリンピック等#図形の性質#三角形の辺の比(内分・外分・二等分線)#数学オリンピック#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
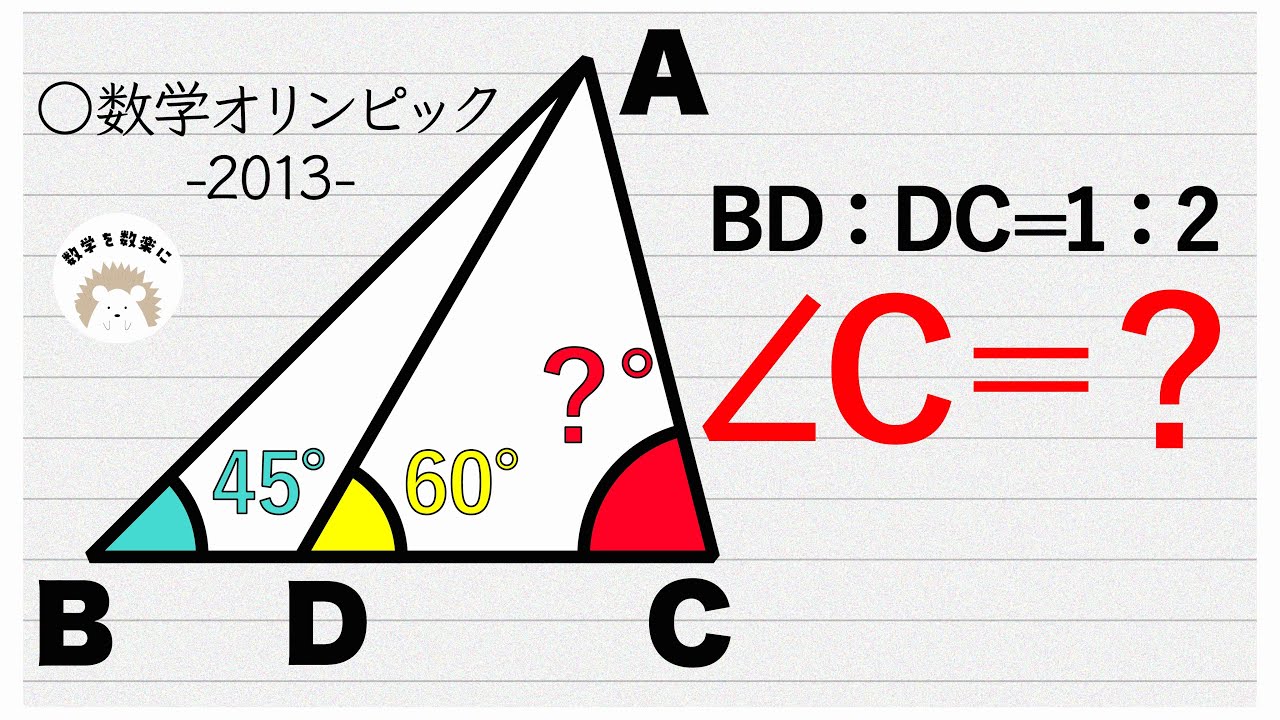
BD:DC=1:2
$\angle C=?$
*図は動画内参照
2013数学オリンピック
この動画を見る
BD:DC=1:2
$\angle C=?$
*図は動画内参照
2013数学オリンピック
福田の数学〜京都大学2022年文系第2問〜条件を満たす経路の総数と漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
下図(※動画参照)の三角柱ABC-DEFにおいて、Aを始点として、辺に沿って
頂点をn回移動する。すなわち、この移動経路
$P_0 \to P_1 \to P_2 \to \ldots \to P_{n-1} \to P_n$ (ただし$P_0=A$)
において、$P_0P_1,P_1P_2,\ldots,P_{n-1}P_n$は全て辺であるとする。
また、同じ頂点を何度通ってよいものとする。このような移動経路で、終点$P_n$がA,B,Cの
いずれかとなるものの総数$a_n$を求めよ。
2022京都大学文系過去問
この動画を見る
下図(※動画参照)の三角柱ABC-DEFにおいて、Aを始点として、辺に沿って
頂点をn回移動する。すなわち、この移動経路
$P_0 \to P_1 \to P_2 \to \ldots \to P_{n-1} \to P_n$ (ただし$P_0=A$)
において、$P_0P_1,P_1P_2,\ldots,P_{n-1}P_n$は全て辺であるとする。
また、同じ頂点を何度通ってよいものとする。このような移動経路で、終点$P_n$がA,B,Cの
いずれかとなるものの総数$a_n$を求めよ。
2022京都大学文系過去問
1分でフェルマーの最終定理の証明できるのか?

大学入試問題#148 京都大学(1972) 積分と極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x \gt 0$
$F(x)=\displaystyle \int_{0}^{x}\displaystyle \frac{t}{(t+1)(t+3)}dt$のとき
$\displaystyle \lim_{ x \to \infty }(F(x)-log\ x)$を求めよ。
出典:1972年京都大学 入試問題
この動画を見る
$x \gt 0$
$F(x)=\displaystyle \int_{0}^{x}\displaystyle \frac{t}{(t+1)(t+3)}dt$のとき
$\displaystyle \lim_{ x \to \infty }(F(x)-log\ x)$を求めよ。
出典:1972年京都大学 入試問題
2022早稲田大(社)整式の剰余

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整式P(x)をx-1で割ると1あまり,$ (x+1)^2 $で割ると3x+2あまる.
P(x)を次の式で割ったあまりは?
(1)$ x+1$ (2)$(x+1)(x-1)$ (3)$(x-1)(x+1)^2$
2022早稲田大過去問
この動画を見る
整式P(x)をx-1で割ると1あまり,$ (x+1)^2 $で割ると3x+2あまる.
P(x)を次の式で割ったあまりは?
(1)$ x+1$ (2)$(x+1)(x-1)$ (3)$(x-1)(x+1)^2$
2022早稲田大過去問
【数Ⅱ】2つの円の位置関係・交点を通る直線または円の方程式【知らないと解けない知識問題】

単元:
#数Ⅱ#図形と方程式#点と直線#円と方程式#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ 2円x^2+y^2-10=0,x^2+y^2+2x-2y-6=0が2点で交わることを示せ.$
この動画を見る
$ 2円x^2+y^2-10=0,x^2+y^2+2x-2y-6=0が2点で交わることを示せ.$
【高校数学】シグマの例題演習~文字の扱いが難しい~ 3-8.5【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$$1,1+2,1+2+3,\cdots,1+2+3+\cdots+n,\cdots$$
となる数列の初項から第k項までの 総和を求めなさい。
この動画を見る
$$1,1+2,1+2+3,\cdots,1+2+3+\cdots+n,\cdots$$
となる数列の初項から第k項までの 総和を求めなさい。
福田の数学・入試問題解説〜東北大学2022年理系第4問〜2つの直線に接し互いに外接する2つの円の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
xy平面の第1象限内において、直線$l:y=mx (m \gt 0)$とx軸の両方に
接している半径aの円をCとし、円Cの中心を通る直線$y=tx (t \gt 0)$を考える。
また、直線lとx軸、および、円Cの全てにそれぞれ1点で接する円の半径をbとする。
ただし、$b \gt a$とする。
(1)mを用いてtを表せ。
(2)tを用いて$\frac{b}{a}$を表せ。
(3)極限値$\lim_{m \to +0}\frac{1}{m}(\frac{b}{a}-1)$を求めよ。
2022東北大学理系過去問
この動画を見る
xy平面の第1象限内において、直線$l:y=mx (m \gt 0)$とx軸の両方に
接している半径aの円をCとし、円Cの中心を通る直線$y=tx (t \gt 0)$を考える。
また、直線lとx軸、および、円Cの全てにそれぞれ1点で接する円の半径をbとする。
ただし、$b \gt a$とする。
(1)mを用いてtを表せ。
(2)tを用いて$\frac{b}{a}$を表せ。
(3)極限値$\lim_{m \to +0}\frac{1}{m}(\frac{b}{a}-1)$を求めよ。
2022東北大学理系過去問
tan

東京大2022理系

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
数列{$a_n$}を次のように定める。
$a_1=1$ , $a_{n+1}={a_n}^2+1(n=1,2,3\cdots)$
(1)正の整数nが3の倍数のとき$a_n$は5の倍数となることを示せ。
(2)$a_n$が$a_k$の倍数となる必要十分条件をk,nを用いて示せ。(k,n:正の整数)
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系
この動画を見る
数列{$a_n$}を次のように定める。
$a_1=1$ , $a_{n+1}={a_n}^2+1(n=1,2,3\cdots)$
(1)正の整数nが3の倍数のとき$a_n$は5の倍数となることを示せ。
(2)$a_n$が$a_k$の倍数となる必要十分条件をk,nを用いて示せ。(k,n:正の整数)
(3)$a_{2022}$と$(a_{8091})^2$の最大公約数を求めよ。
2022東京大学理系
大学入試問題#147 三重大学(2020) 積分の応用

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$x \geqq 1$のとき
$x \geqq 1+log\ x$を示せ
(2)
$\displaystyle \int_{1}^{e}\displaystyle \frac{log\ x}{1+log\ x}dx \geqq \displaystyle \frac{1}{2}$を示せ
出典:2020年三重大学 入試問題
この動画を見る
(1)
$x \geqq 1$のとき
$x \geqq 1+log\ x$を示せ
(2)
$\displaystyle \int_{1}^{e}\displaystyle \frac{log\ x}{1+log\ x}dx \geqq \displaystyle \frac{1}{2}$を示せ
出典:2020年三重大学 入試問題
解けるように作られた問題

単元:
#数Ⅱ#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^3-x-1=0 $の実数解を$ \alpha $とするとき,
$ \sqrt[3]{3\alpha^2-4\alpha}+\sqrt[3]{3\alpha^2+4\alpha+2}$の値を求めよ.
この動画を見る
$ x^3-x-1=0 $の実数解を$ \alpha $とするとき,
$ \sqrt[3]{3\alpha^2-4\alpha}+\sqrt[3]{3\alpha^2+4\alpha+2}$の値を求めよ.
内閣の二等分線 西京高校 2022 入試から観る数学の世界
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
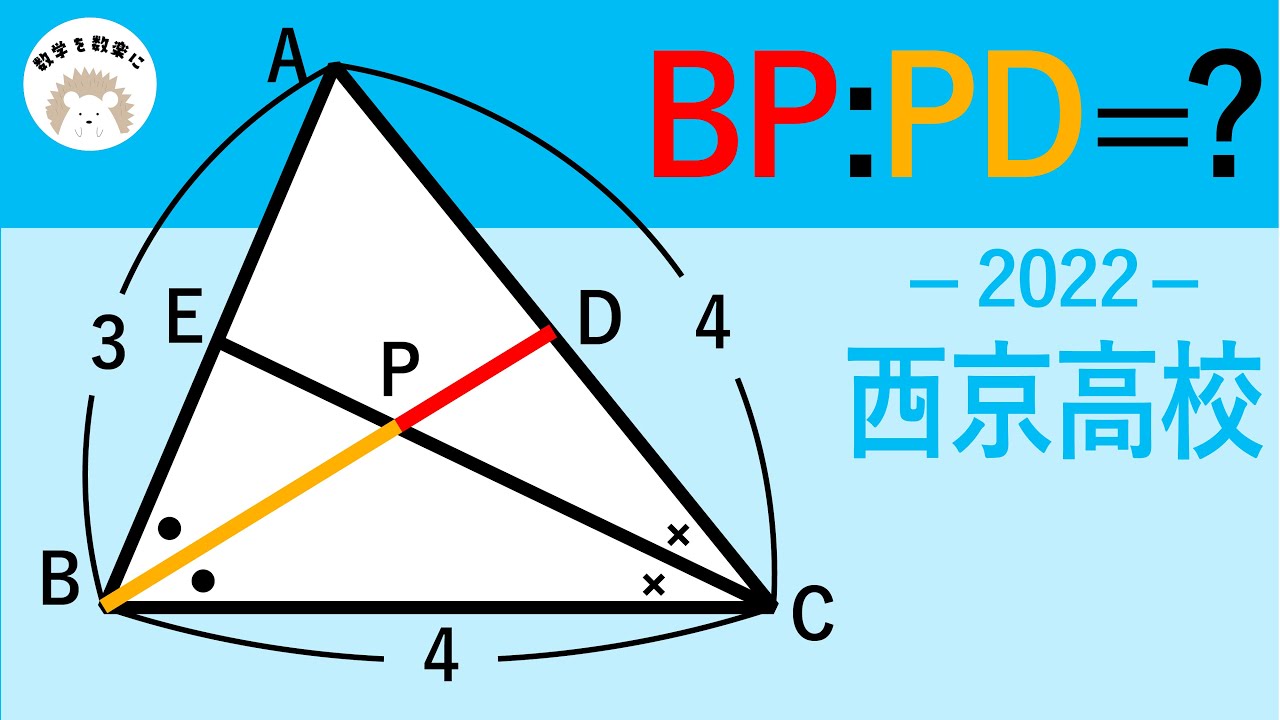
BP:PD=?
*図は動画内参照
2022西京高等学校
この動画を見る
BP:PD=?
*図は動画内参照
2022西京高等学校
福田の入試問題解説〜東京大学2022年文系第4問〜複雑な反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
{\Large{\boxed{4}}}\ Oを原点とする座標平面上で考える。0以上の整数kに対して、ベクトル\overrightarrow{ v_k }を\\
\overrightarrow{ v_k }=(\cos\frac{2k\pi}{3}, \sin\frac{2k\pi}{3})\\
と定める。投げたとき表と裏がどちらも\frac{1}{2}の確率で出るコインをN回投げて、\\
座標平面上に点X_0,X_1,X_2,\ldots,X_Nを以下の規則(\textrm{i}),(\textrm{ii})に従って定める。\\
(\textrm{i})X_0はOにある。\\
(\textrm{ii})nを1以上N以下の整数とする。X_{n-1}が定まったとし、\\
X_nを次のように定める。\\
・n回目のコイン投げで表が出た場合、\overrightarrow{ OX_n }=\overrightarrow{ OX_{n-1} }+\overrightarrow{ v_k }によりX_nを定める。\\
ただし、kは1回目からn回目までのコイン投げで裏が出た回数とする。\\
・n回目のコイン投げで裏が出た場合、X_nをX_{n-1}と定める。\\
(1)N=5とする。X_5がOにある確率を求めよ。\\
(2)N=98とする。X_{98}がOにあり、かつ、表が90回、裏が8回出る確率を求めよ。
\end{eqnarray}
2022東京大学文系過去問
この動画を見る
\begin{eqnarray}
{\Large{\boxed{4}}}\ Oを原点とする座標平面上で考える。0以上の整数kに対して、ベクトル\overrightarrow{ v_k }を\\
\overrightarrow{ v_k }=(\cos\frac{2k\pi}{3}, \sin\frac{2k\pi}{3})\\
と定める。投げたとき表と裏がどちらも\frac{1}{2}の確率で出るコインをN回投げて、\\
座標平面上に点X_0,X_1,X_2,\ldots,X_Nを以下の規則(\textrm{i}),(\textrm{ii})に従って定める。\\
(\textrm{i})X_0はOにある。\\
(\textrm{ii})nを1以上N以下の整数とする。X_{n-1}が定まったとし、\\
X_nを次のように定める。\\
・n回目のコイン投げで表が出た場合、\overrightarrow{ OX_n }=\overrightarrow{ OX_{n-1} }+\overrightarrow{ v_k }によりX_nを定める。\\
ただし、kは1回目からn回目までのコイン投げで裏が出た回数とする。\\
・n回目のコイン投げで裏が出た場合、X_nをX_{n-1}と定める。\\
(1)N=5とする。X_5がOにある確率を求めよ。\\
(2)N=98とする。X_{98}がOにあり、かつ、表が90回、裏が8回出る確率を求めよ。
\end{eqnarray}
2022東京大学文系過去問
大学入試問題#146 東京工業大学(1966) 定積分
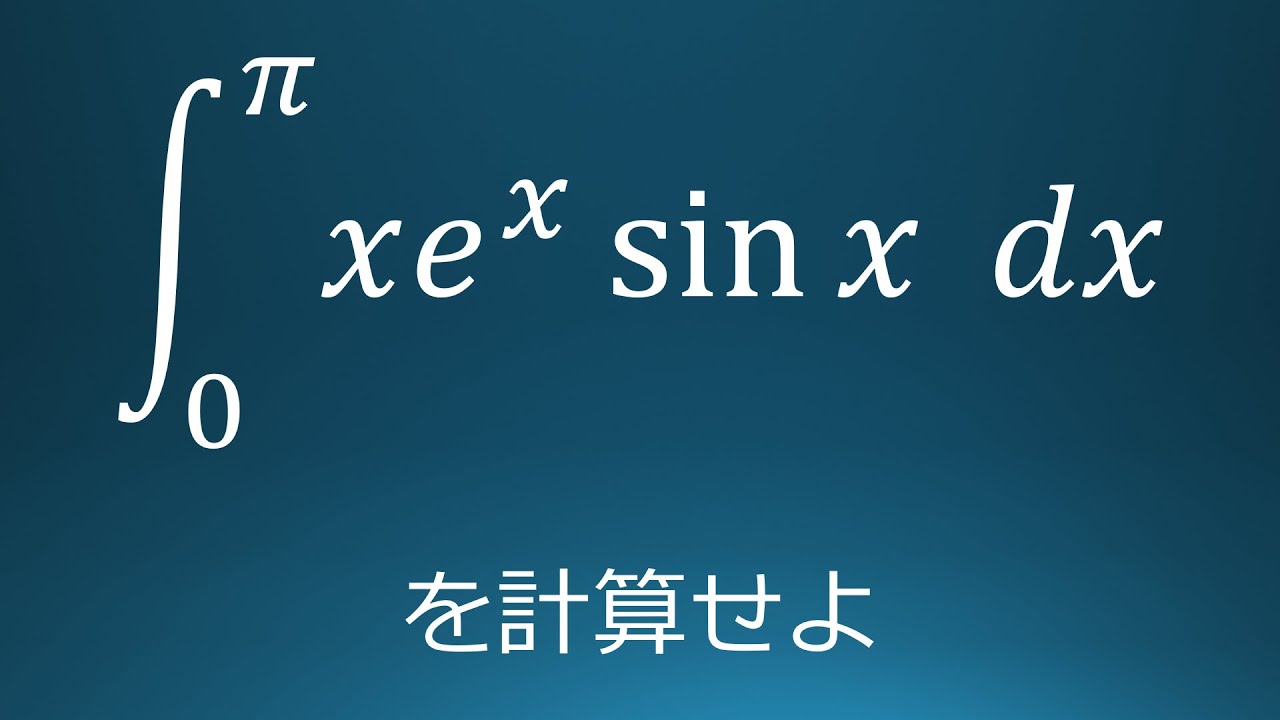
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi}xe^x\sin\ x\ dx$を計算せよ。
出典:1966年東京工業大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi}xe^x\sin\ x\ dx$を計算せよ。
出典:1966年東京工業大学 入試問題
素数

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ n^4-11n^2+49 $が素数となる整数 $ n$を求めよ.
この動画を見る
$ n^4-11n^2+49 $が素数となる整数 $ n$を求めよ.
素数

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n^4-11n^2+49$が素数となる整数$n$を求めよ.
この動画を見る
$n^4-11n^2+49$が素数となる整数$n$を求めよ.
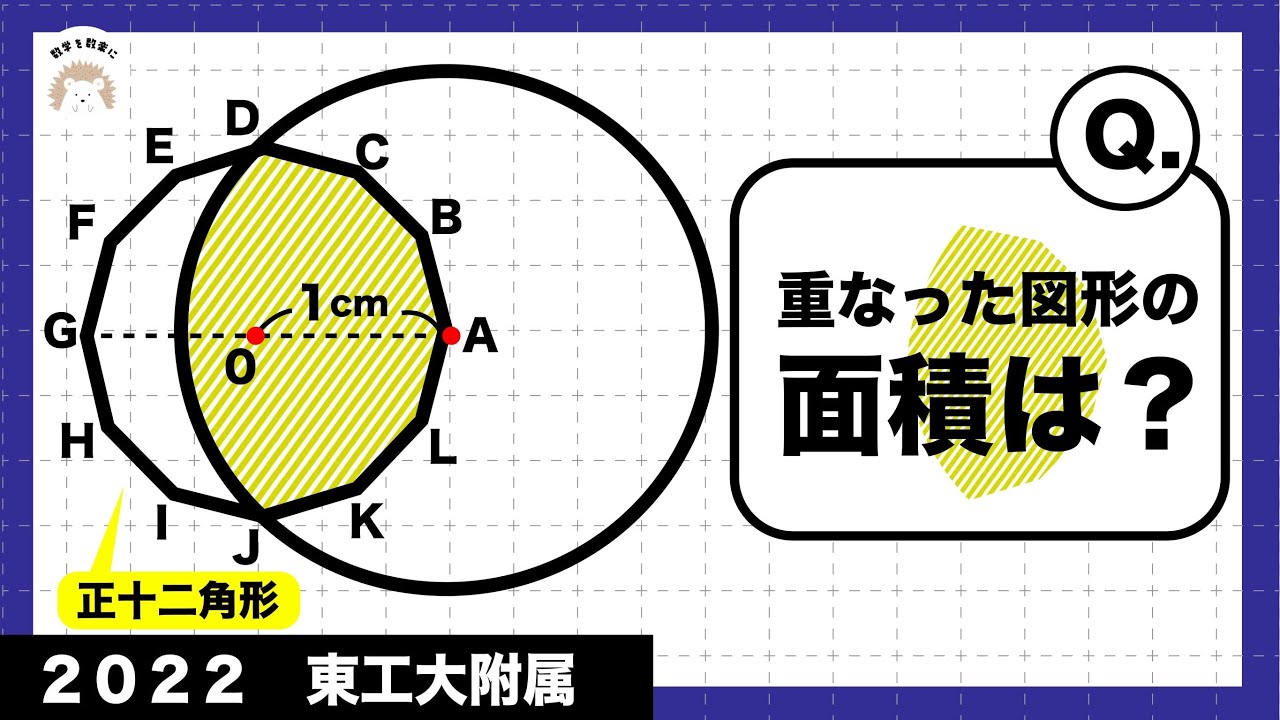
正十二角形と円 東工大附属
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
重なった図形の面積は?
*図は動画内参照
2022東京工業大学附属科学技術高等学校
この動画を見る
重なった図形の面積は?
*図は動画内参照
2022東京工業大学附属科学技術高等学校
大学入試問題#145 自治医科大(2004) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$x^2-3ax+2a-3=0$が2つの整数解をもつように$a$が定まっている。
$a^2+3$の値を求めよ。
出典:2004年自治医科大学 入試問題
この動画を見る
$x^2-3ax+2a-3=0$が2つの整数解をもつように$a$が定まっている。
$a^2+3$の値を求めよ。
出典:2004年自治医科大学 入試問題
福田の数学・入試問題解説〜東北大学2022年理系第3問〜無限級数の和とはさみうちの原理

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
正の整数nに対して、
$S_n=\sum_{k=1}^n(\sqrt{1+\frac{k}{n^2}}-1)$
とする。
(1)正の実数xに対して、次の不等式が成り立つことを示せ。
$\frac{x}{2+x} \leqq \sqrt{1+x}-1 \leqq \frac{x}{2}$
(2)極限値$\lim_{n \to \infty}S_n$を求めよ。
2022東北大学理系過去問
この動画を見る
正の整数nに対して、
$S_n=\sum_{k=1}^n(\sqrt{1+\frac{k}{n^2}}-1)$
とする。
(1)正の実数xに対して、次の不等式が成り立つことを示せ。
$\frac{x}{2+x} \leqq \sqrt{1+x}-1 \leqq \frac{x}{2}$
(2)極限値$\lim_{n \to \infty}S_n$を求めよ。
2022東北大学理系過去問
解けるように作られた方程式
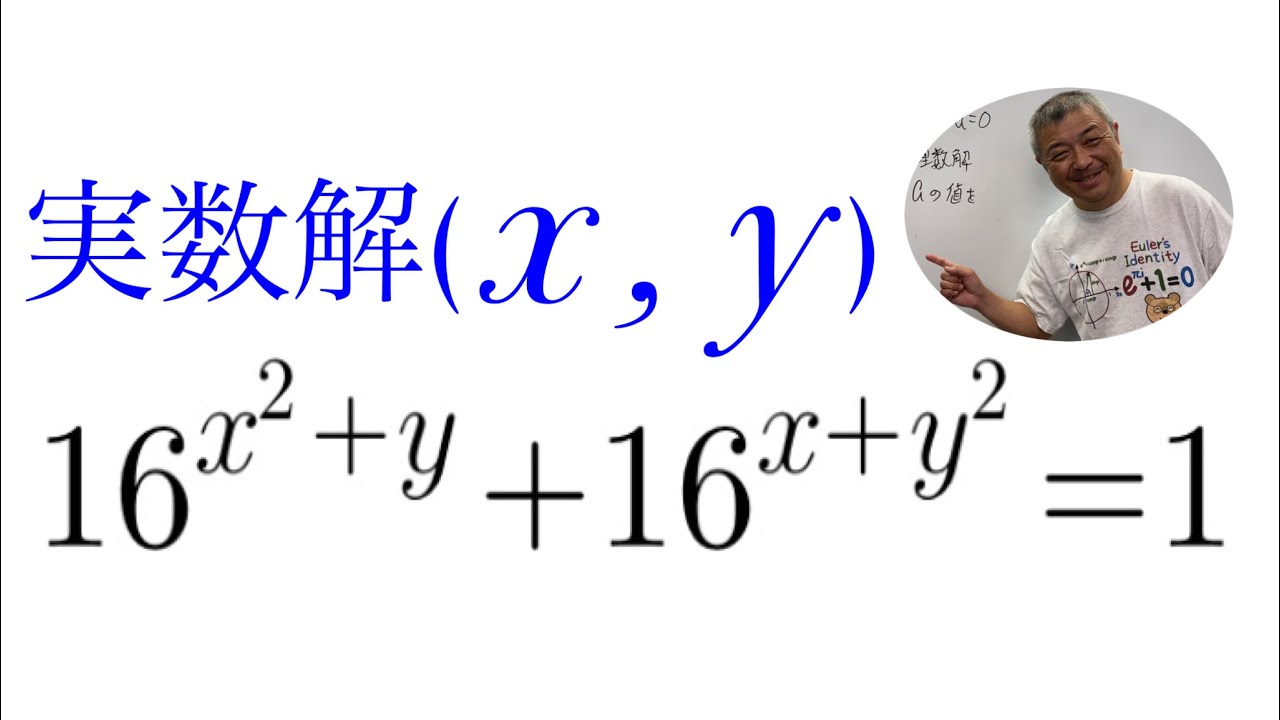
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解$(x,y)$を求めよ.
$ 16^{x^2+y}+16^{x+y^2}=1$
この動画を見る
実数解$(x,y)$を求めよ.
$ 16^{x^2+y}+16^{x+y^2}=1$
指数方程式
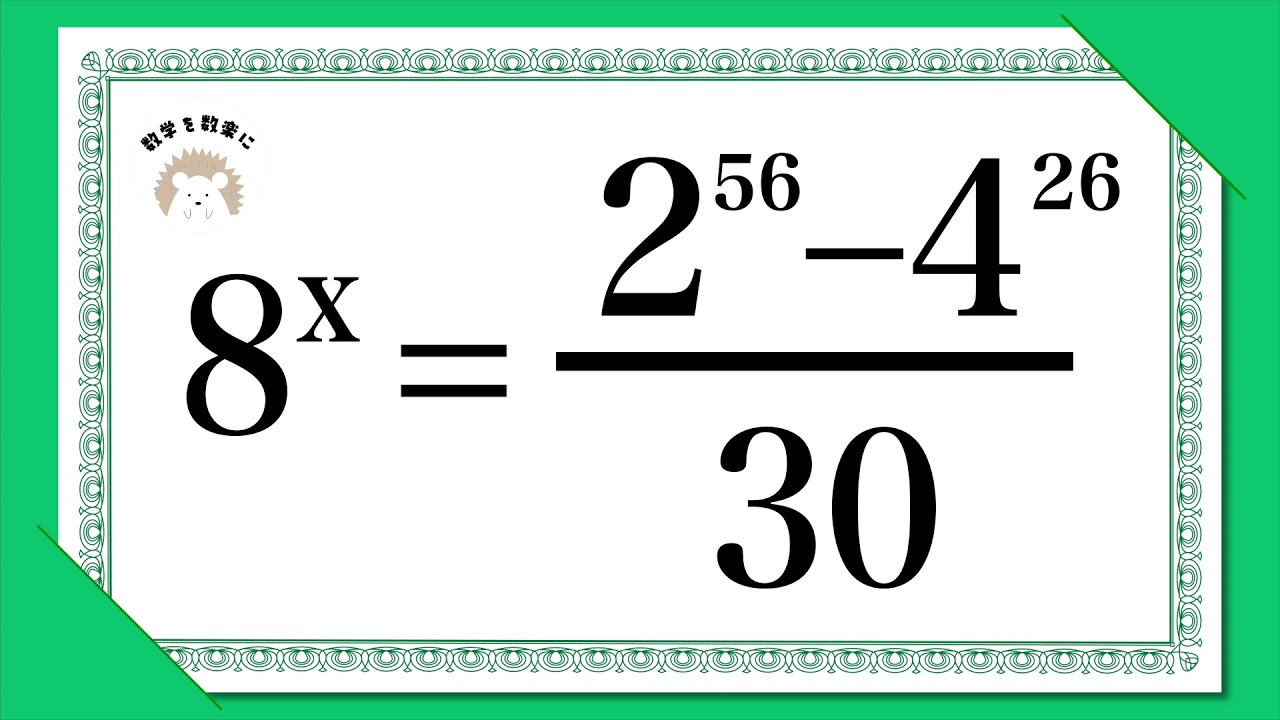
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$8^x=\frac{2^{56}-4^{26}}{30}$のときx=?
この動画を見る
$8^x=\frac{2^{56}-4^{26}}{30}$のときx=?
【理数個別の過去問解説】2019年度 明治大学 経営学部 数学 第3問解説(1)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
〔Ⅲ〕$x+2y=5、x\gt 0,y\gt 0$を満たす実数x,yがある。
(1) $2x^2+y^2$の最小値
(2) $\log_{10}x+2\log_{10}y$ の最大値
(3) $\dfrac{1}{x}+\dfrac{2}{y}$ の最小値
この動画を見る
〔Ⅲ〕$x+2y=5、x\gt 0,y\gt 0$を満たす実数x,yがある。
(1) $2x^2+y^2$の最小値
(2) $\log_{10}x+2\log_{10}y$ の最大値
(3) $\dfrac{1}{x}+\dfrac{2}{y}$ の最小値
福田の入試問題解説〜東京大学2022年文系第3問〜漸化式と最大公約数

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
問題文全文(内容文):
数列$\left\{a_n\right\}$を次のように定める。
$a_1=4, a_{n+1}=a_n^2+n(n+2)$
(1)$a_{2022}$を3で割った余りを求めよ。
(2)$a_{2022},a_{2023},a_{2024}$の最大公約数を求めよ。
2022東京大学文系過去問
この動画を見る
数列$\left\{a_n\right\}$を次のように定める。
$a_1=4, a_{n+1}=a_n^2+n(n+2)$
(1)$a_{2022}$を3で割った余りを求めよ。
(2)$a_{2022},a_{2023},a_{2024}$の最大公約数を求めよ。
2022東京大学文系過去問
福田の数学・入試問題解説〜東北大学2022年理系第2問〜4次関数の極値と最小値

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
aを実数とし、実数xの関数$f(x)=(x^2+3x+a)(x+1)^2$を考える。
(1)f(x)の最小値が負となるようなaのとりうる値の範囲を求めよ。
(2)$a \lt 2$のとき、f(x)は2つの極小値をもつ。このときf(x)が極小となる
xの値を$\alpha_1,\alpha_2(\alpha_1 \lt \alpha_2)$とする。
$f(\alpha_1) \lt f(\alpha_2)$を示せ。
(3)f(x)が$x \lt \beta$において単調減少し、かつ、$x=\beta$において最小値をとるとする。
このとき、aのとりうる値の範囲を求めよ。
2022東北大学理系過去問
この動画を見る
aを実数とし、実数xの関数$f(x)=(x^2+3x+a)(x+1)^2$を考える。
(1)f(x)の最小値が負となるようなaのとりうる値の範囲を求めよ。
(2)$a \lt 2$のとき、f(x)は2つの極小値をもつ。このときf(x)が極小となる
xの値を$\alpha_1,\alpha_2(\alpha_1 \lt \alpha_2)$とする。
$f(\alpha_1) \lt f(\alpha_2)$を示せ。
(3)f(x)が$x \lt \beta$において単調減少し、かつ、$x=\beta$において最小値をとるとする。
このとき、aのとりうる値の範囲を求めよ。
2022東北大学理系過去問
「6÷2(1+2)」簡単そうで解けない...?

