 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【中学生の方が解ける…!?】図形:駿台甲府高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#数Ⅰ#図形と計量
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
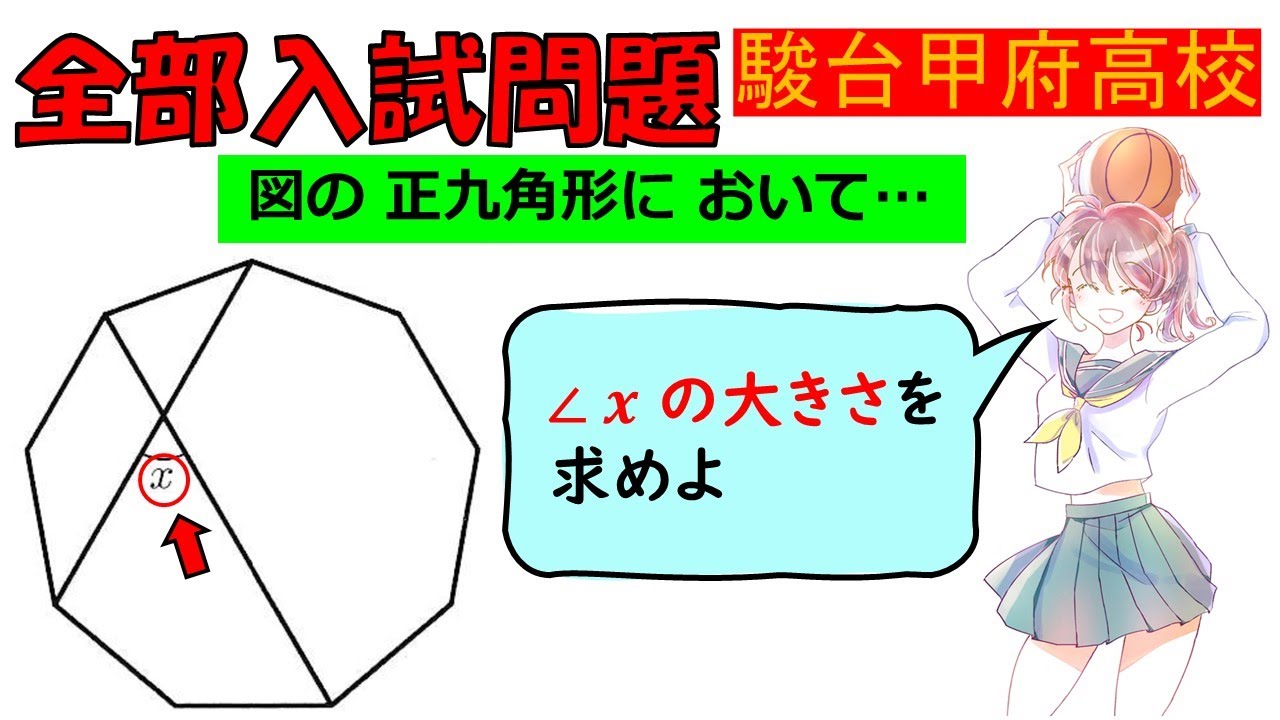
問題文全文(内容文):
図の正九角形において
$\angle x$の大きさを求めよ
この動画を見る
図の正九角形において
$\angle x$の大きさを求めよ
福田のおもしろ数学421〜2つの条件を満たす素数p,qを求める

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$q^2-4$が$p$で割り切れ
$p^2-1$が$q$で割り切れる
ような素数$p,q$は?
この動画を見る
$q^2-4$が$p$で割り切れ
$p^2-1$が$q$で割り切れる
ような素数$p,q$は?
福田の数学〜東京大学2025理系第2問〜はさみうちの原理を利用する極限

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
(1)$x\gt0$のとき、
不等式$\log x \leqq x - 1$を示せ。
(2)次の極限を求めよ。
$\displaystyle \lim_{n\to\infty} n \displaystyle \int_{1}^{2} \log \left(\dfrac{1+x^{\frac{1}{n}}}{2}\right)dx$
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{2}$
(1)$x\gt0$のとき、
不等式$\log x \leqq x - 1$を示せ。
(2)次の極限を求めよ。
$\displaystyle \lim_{n\to\infty} n \displaystyle \int_{1}^{2} \log \left(\dfrac{1+x^{\frac{1}{n}}}{2}\right)dx$
$2025$年東京大学理系過去問題
【数Ⅱ】【複素数と方程式】高次方程式3 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
立方体の底面の縦を1㎝、横を2㎝それぞれ伸ばし、高さを1㎝縮めて直方体を作ったら、体積が50%増加した。もとの立方体の1辺の長さを求めよ。
2乗すると8+6iとなる複素数を求めよ。
3次方程式x³-3x²-2x+7=0の3つの解をα,β,γとするとき、次の式の値を求めよ。
(1)(1/α)+(1/β)+(1/γ)
(2)α²+β²+γ²
(3)α³+β³+γ³
(4)(1-α)(1-β)(1-γ)
(5)(α+β)(β+γ)(γ+α)
この動画を見る
立方体の底面の縦を1㎝、横を2㎝それぞれ伸ばし、高さを1㎝縮めて直方体を作ったら、体積が50%増加した。もとの立方体の1辺の長さを求めよ。
2乗すると8+6iとなる複素数を求めよ。
3次方程式x³-3x²-2x+7=0の3つの解をα,β,γとするとき、次の式の値を求めよ。
(1)(1/α)+(1/β)+(1/γ)
(2)α²+β²+γ²
(3)α³+β³+γ³
(4)(1-α)(1-β)(1-γ)
(5)(α+β)(β+γ)(γ+α)
【数Ⅱ】【複素数と方程式】高次方程式2 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
3次方程式x³-5x²+ax+b=0が3+2iを解にもつとき、実数の定数a, bの値と他の解を求めよ。
3次方程式x³+ax²+bx+3a-20=0が2重解-2をもつとき、実数の定数a, bの値と他の解を求めよ。
3次方程式x³+3x²+(a-4)x-a=0が2重解をもつとき、定数aの値を求めよ。
この動画を見る
3次方程式x³-5x²+ax+b=0が3+2iを解にもつとき、実数の定数a, bの値と他の解を求めよ。
3次方程式x³+ax²+bx+3a-20=0が2重解-2をもつとき、実数の定数a, bの値と他の解を求めよ。
3次方程式x³+3x²+(a-4)x-a=0が2重解をもつとき、定数aの値を求めよ。
【数Ⅱ】【複素数と方程式】高次方程式1 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の方程式を解け。
(1)4x³+3x-2=0
(2)2x³-7x²+2=0
(3)(x-1)(x-2)(x-3)=4・3・2
(4)(x²-2x)²-(x²-2x)-6=0
(5)x⁴+x²+1=0
(6)(x²-5x+1)(x²-5x+9)+15=0
1の3乗根のうち、虚数であるものの1つをωとする。次の式の値を求めよ。
(1)ω⁶+ω³+1
(2)ω⁸+ω⁴+1
(3)ω²⁰⁰+ω¹⁰⁰
4次方程式x⁴-3x³+ax²+bx-4=0が1と2を解にもつとき、定数a, bの値と他の解を求めよ。
この動画を見る
次の方程式を解け。
(1)4x³+3x-2=0
(2)2x³-7x²+2=0
(3)(x-1)(x-2)(x-3)=4・3・2
(4)(x²-2x)²-(x²-2x)-6=0
(5)x⁴+x²+1=0
(6)(x²-5x+1)(x²-5x+9)+15=0
1の3乗根のうち、虚数であるものの1つをωとする。次の式の値を求めよ。
(1)ω⁶+ω³+1
(2)ω⁸+ω⁴+1
(3)ω²⁰⁰+ω¹⁰⁰
4次方程式x⁴-3x³+ax²+bx-4=0が1と2を解にもつとき、定数a, bの値と他の解を求めよ。
【数Ⅱ】【複素数と方程式】剰余の定理と因数定理3 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
x⁵¹+1をx²-1で割ったときの余りを求めよ。
(1)x=√2-1のとき、x⁴+3x³-5x²-10x+7の値を求めよ。
(2)x=1-√5iのとき、x⁴-4x³+14x²-19x+26の値を求めよ。
組立除法を用いて、次の多項式Aを多項式Bで割った商と余りを求めよ。
(1)A=4x³+x²+6x-5, B=x-1
(2)A=3x³-x²+3, B=x+2
(3)A=2x³-7x²+8x-8, B=2x-3
この動画を見る
x⁵¹+1をx²-1で割ったときの余りを求めよ。
(1)x=√2-1のとき、x⁴+3x³-5x²-10x+7の値を求めよ。
(2)x=1-√5iのとき、x⁴-4x³+14x²-19x+26の値を求めよ。
組立除法を用いて、次の多項式Aを多項式Bで割った商と余りを求めよ。
(1)A=4x³+x²+6x-5, B=x-1
(2)A=3x³-x²+3, B=x+2
(3)A=2x³-7x²+8x-8, B=2x-3
【数Ⅱ】【複素数と方程式】剰余の定理と因数定理2 ※問題文は概要欄

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#複素数と方程式#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
多項式P(x)を(x-1)(x+2)で割ると余りが3x-1である。P(x)をx-1およびx-2で割ったときの余りを、それぞれ求めよ。
多項式P(x)をx-2で割ると余りが5, x-3で割ると余りが9である。P(x)を(x-2)(x-3)で割ったときの余りを求めよ。
多項式P(x)をx²-3x+2で割ると余りが-x+4, x²-4x+3で割ると余りが3xである。P(x)をx²-5x+6で割ったときの余りを求めよ。
この動画を見る
多項式P(x)を(x-1)(x+2)で割ると余りが3x-1である。P(x)をx-1およびx-2で割ったときの余りを、それぞれ求めよ。
多項式P(x)をx-2で割ると余りが5, x-3で割ると余りが9である。P(x)を(x-2)(x-3)で割ったときの余りを求めよ。
多項式P(x)をx²-3x+2で割ると余りが-x+4, x²-4x+3で割ると余りが3xである。P(x)をx²-5x+6で割ったときの余りを求めよ。
福田の数学〜東京大学2025理系第1問〜媒介変数表示で表された曲線の面積と曲線の長さ

単元:
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
座標平面上の点
$A(0,0),B(0,1),C(1,1),D(1,0)$を考える。
実数$0\lt t \lt 1$に対して、
線分$AB,BC,CD$を$t:(1-t)$に内分する点を
それぞれ$S_t,T_t$とする。
さらに、線分$S_tT_t$を$t:(1-t)$に内分する点を
$U_t$とする。
また、点$A$を$U_0$、点$D$を$U_1$とする。
(1)点$U_t$の座標を求めよ。
(2)$t$が$0\leqq t\leqq 1$の範囲を動くときに
点$U_t$描く曲線と、
線分$AD$で囲まれた部分の面積を求めよ。
(3)$a$を$0\lt a\lt 1$を満たす実数とする。
$t$が$0\leqq t \leqq a$の範囲を動くときに点$U_t$が
描く曲線の長さを、$a$の多項式の形で求めよ。
図は動画内参照
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{1}$
座標平面上の点
$A(0,0),B(0,1),C(1,1),D(1,0)$を考える。
実数$0\lt t \lt 1$に対して、
線分$AB,BC,CD$を$t:(1-t)$に内分する点を
それぞれ$S_t,T_t$とする。
さらに、線分$S_tT_t$を$t:(1-t)$に内分する点を
$U_t$とする。
また、点$A$を$U_0$、点$D$を$U_1$とする。
(1)点$U_t$の座標を求めよ。
(2)$t$が$0\leqq t\leqq 1$の範囲を動くときに
点$U_t$描く曲線と、
線分$AD$で囲まれた部分の面積を求めよ。
(3)$a$を$0\lt a\lt 1$を満たす実数とする。
$t$が$0\leqq t \leqq a$の範囲を動くときに点$U_t$が
描く曲線の長さを、$a$の多項式の形で求めよ。
図は動画内参照
$2025$年東京大学理系過去問題
【数Ⅱ】【微分法と積分法】方程式の解の個数5 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
方程式2x³-3x²-36x=aが1個の正の解と2個の負の解をもつように、定数aの値の範囲を定めよ。
この動画を見る
方程式2x³-3x²-36x=aが1個の正の解と2個の負の解をもつように、定数aの値の範囲を定めよ。
福田の数学〜旧・東京工業大学、東京科学大学2025理系第1問〜逆関数の定積分

単元:
#大学入試過去問(数学)#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$$\quad$関数$f(x)$を$x\geqq 0$に対して
$f(x)=x\log(1+x)$と定める。
(1)不定積分$\displaystyle \int x\log(1+x)dx$を求めよ。
(2)$y=f(x) \quad (x\geqq 0)$の逆関数を
$y=g(x) \quad (x\geqq 0)$とする。
また、$a,b$を$g(a)=1,g(b)=2$となる
実数となる。
このとき定積分$I=\displaystyle \int_{a}{b} g(x)dx$の値を求めよ。
(3)関数$P(x)$を$x\geqq 0$に対して
$P(x)=\displaystyle \int_{0}^{x}\sqrt{1+f(t)dt}$と定める。
このとき、$y=P(x)$について、
定義域を$x\geqq 0$とする逆関数
$y=Q(x)$が微分可能であることは
説明なしに認めてよい。
関数$R(x)$を$x\geqq 0$に対して
$R(x)=\displaystyle int_{0}^{P(x)}\dfrac{1}{Q'(\upsilon)}$と定めるとき、
$R(x)$を求めよ。
図は動画内参照
$2025$年東京科学大学(旧・東京工業大学)理系過去問題
この動画を見る
$\boxed{1}$$\quad$関数$f(x)$を$x\geqq 0$に対して
$f(x)=x\log(1+x)$と定める。
(1)不定積分$\displaystyle \int x\log(1+x)dx$を求めよ。
(2)$y=f(x) \quad (x\geqq 0)$の逆関数を
$y=g(x) \quad (x\geqq 0)$とする。
また、$a,b$を$g(a)=1,g(b)=2$となる
実数となる。
このとき定積分$I=\displaystyle \int_{a}{b} g(x)dx$の値を求めよ。
(3)関数$P(x)$を$x\geqq 0$に対して
$P(x)=\displaystyle \int_{0}^{x}\sqrt{1+f(t)dt}$と定める。
このとき、$y=P(x)$について、
定義域を$x\geqq 0$とする逆関数
$y=Q(x)$が微分可能であることは
説明なしに認めてよい。
関数$R(x)$を$x\geqq 0$に対して
$R(x)=\displaystyle int_{0}^{P(x)}\dfrac{1}{Q'(\upsilon)}$と定めるとき、
$R(x)$を求めよ。
図は動画内参照
$2025$年東京科学大学(旧・東京工業大学)理系過去問題
福田のおもしろ数学420〜間に左右の数の和を次々と書き足していくときの総和

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
黒板の両端に$1$が書かれている。
$1$番の生徒がその間に
左右の数の和である$2$を書く。
$2$番の生徒が$2$カ所の間に
左右の数の和である$3$を書く。
この操作を繰り返したとき、
$n$番の生徒が書き終えたとき、数字の合計はいくらか?
図は動画内参照
この動画を見る
黒板の両端に$1$が書かれている。
$1$番の生徒がその間に
左右の数の和である$2$を書く。
$2$番の生徒が$2$カ所の間に
左右の数の和である$3$を書く。
この操作を繰り返したとき、
$n$番の生徒が書き終えたとき、数字の合計はいくらか?
図は動画内参照
【数Ⅱ】【微分法と積分法】方程式の解の個数8 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線C:y=x³+3x²について、次の問いに答えよ。
(1)C上の点P(t,t³+3t)におけるCの接線が点A(0,a)を通る時、等式2t³+3t²+a=0が成り立つことを示せ。
(2)Aを通るCの接線が3本存在するとき、aの値の範囲を求めよ。
この動画を見る
曲線C:y=x³+3x²について、次の問いに答えよ。
(1)C上の点P(t,t³+3t)におけるCの接線が点A(0,a)を通る時、等式2t³+3t²+a=0が成り立つことを示せ。
(2)Aを通るCの接線が3本存在するとき、aの値の範囲を求めよ。
【数Ⅱ】【微分法と積分法】方程式の解の個数7 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
方程式x³-3ax+a=0が異なる3個の実数解をもつとき、定数aの値の範囲を求めよ。
この動画を見る
方程式x³-3ax+a=0が異なる3個の実数解をもつとき、定数aの値の範囲を求めよ。
【数Ⅱ】【微分法と積分法】方程式の解の個数6 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
4次方程式x⁴-4x³-2x²+12x-a=0が異なる4個の実数解を持ち、そのうち2個は正、残りの2個は負であるとき、定数aの値の範囲を求めよ。
この動画を見る
4次方程式x⁴-4x³-2x²+12x-a=0が異なる4個の実数解を持ち、そのうち2個は正、残りの2個は負であるとき、定数aの値の範囲を求めよ。
【数Ⅱ】【微分法と積分法】極大極小の条件2 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数f(x)=x⁴+4x³+2ax²が極大値と極小値を持つように,定数aの値の範囲を定めよ。
この動画を見る
関数f(x)=x⁴+4x³+2ax²が極大値と極小値を持つように,定数aの値の範囲を定めよ。
福田のおもしろ数学419〜条件を満たす自然数nが存在するような2つの素数の差を求める

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$p,q$は素数$(p \lt q)$
$\dfrac{p}{p+1}+\dfrac{q+1}{q}=\dfrac{2n}{n+2}$
を満たす正の整数$n$が存在する。
このとき、$q-p$の値をすべて求めよ。
この動画を見る
$p,q$は素数$(p \lt q)$
$\dfrac{p}{p+1}+\dfrac{q+1}{q}=\dfrac{2n}{n+2}$
を満たす正の整数$n$が存在する。
このとき、$q-p$の値をすべて求めよ。
【数Ⅱ】【微分法と積分法】極大極小の条件1 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数f(x)=x³+ax²+bx+cについて,次の問に答えよ。
(1)x=1で極大となるための条件を求めよ。
(2)x=-2で極小となるための条件を求めよ。
この動画を見る
関数f(x)=x³+ax²+bx+cについて,次の問に答えよ。
(1)x=1で極大となるための条件を求めよ。
(2)x=-2で極小となるための条件を求めよ。
福田のおもしろ数学418〜条件を満たす3つの数を割りきれるようにすることが可能か不可能かの考察

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
十の位が$a$,一の位が$b$である数を$\overline{ab}$で表す。
$0$以外の$1$桁の異なる$3$つの数$a,b,c$に対して
$\overline{ab}$が$c$で割り切れ、$\overline{bc}$が$a$で割り切れ
$\overline{ca}$が$b$で割り切れることは可能か?
この動画を見る
十の位が$a$,一の位が$b$である数を$\overline{ab}$で表す。
$0$以外の$1$桁の異なる$3$つの数$a,b,c$に対して
$\overline{ab}$が$c$で割り切れ、$\overline{bc}$が$a$で割り切れ
$\overline{ca}$が$b$で割り切れることは可能か?
【数Ⅱ】【微分法と積分法】極値の場合分け ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
aは定数とする。次の各場合に、関数y=x(x-a)²の極値を調べよ。
(1)a<0
(2)a=0
(3)a>0
この動画を見る
aは定数とする。次の各場合に、関数y=x(x-a)²の極値を調べよ。
(1)a<0
(2)a=0
(3)a>0
【数Ⅱ】【微分法と積分法】極値を持つ条件 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件に適するように、定数aの値の範囲を、それぞれ定めよ。
(1)関数$f(x)=\frac{1}{3}x^3+ax^2+(a+2)x+1$が極値をもつ。
(2)関数$g(x)=x^3+ax^2-3ax+2$が極値をもたない。
この動画を見る
次の条件に適するように、定数aの値の範囲を、それぞれ定めよ。
(1)関数$f(x)=\frac{1}{3}x^3+ax^2+(a+2)x+1$が極値をもつ。
(2)関数$g(x)=x^3+ax^2-3ax+2$が極値をもたない。
【数Ⅱ】【微分法と積分法】微分と接線7 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つの曲線y=x²,y=-(x-2)²の共通接線の方程式を求めよ。
この動画を見る
2つの曲線y=x²,y=-(x-2)²の共通接線の方程式を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線6 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つの曲線y=x²+2,y=x²+ax+3の交点をPとする。Pにおけるそれぞれの曲線の接線が垂直であるとき,定数aの値を求めよ。
この動画を見る
2つの曲線y=x²+2,y=x²+ax+3の交点をPとする。Pにおけるそれぞれの曲線の接線が垂直であるとき,定数aの値を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線5 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1)曲線y=x³+ax+1が直線y=2x-1に接するとき,定数aの値を求めよ。
(2)曲線y=x³+x²と放物線y=x²+ax+16は,ともにある点Pを通り,Pにおいて共通の接線を持つ。このとき、定数aの値と接線の方程式を求めよ。
この動画を見る
(1)曲線y=x³+ax+1が直線y=2x-1に接するとき,定数aの値を求めよ。
(2)曲線y=x³+x²と放物線y=x²+ax+16は,ともにある点Pを通り,Pにおいて共通の接線を持つ。このとき、定数aの値と接線の方程式を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線4 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線y=2x²-4x+3上の点A(0,3)を通り,点Aにおける曲線の接線に垂直な直線の方程式を求めよ。
この動画を見る
曲線y=2x²-4x+3上の点A(0,3)を通り,点Aにおける曲線の接線に垂直な直線の方程式を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線3 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線y=-x³+4x上の点(-2,0)における接線が,この曲線と交わるもう1つの点のx座標を求めよ。
この動画を見る
曲線y=-x³+4x上の点(-2,0)における接線が,この曲線と交わるもう1つの点のx座標を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線2 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
曲線y=x³+3x²-6 について,傾きが9である接線の方程式を求めよ。
この動画を見る
曲線y=x³+3x²-6 について,傾きが9である接線の方程式を求めよ。
【数Ⅱ】【微分法と積分法】微分と接線1 ※問題文は概要欄

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#微分法と積分法#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の曲線に,与えられた点から引いた接線の方程式と,接点の座標を求めよ。
(1) y=x²+3x+4 (0,0)
(2) y=x²-x+3 (1,-1)
(3) y=x³+2 (0,4)
この動画を見る
次の曲線に,与えられた点から引いた接線の方程式と,接点の座標を求めよ。
(1) y=x²+3x+4 (0,0)
(2) y=x²-x+3 (1,-1)
(3) y=x³+2 (0,4)
福田のおもしろ数学417〜条件付きの不等式の証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数列$\{a_n\}$が$a_1=0,a_2=1$
$a_n=5a_{n-1}-a_{n-2} \quad (n \geqq 3)$
を満たしている。
$a_n$が
(1)$5$で割り切れる
(2)$15$で割り切れる
となる$n$を求めて下さい。
この動画を見る
数列$\{a_n\}$が$a_1=0,a_2=1$
$a_n=5a_{n-1}-a_{n-2} \quad (n \geqq 3)$
を満たしている。
$a_n$が
(1)$5$で割り切れる
(2)$15$で割り切れる
となる$n$を求めて下さい。
【数A】【場合の数と確率】くじを引く順番と確率 ※問題文は概要欄

単元:
#数A#場合の数と確率#確率#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
10本のくじの中に当たりくじが2本ある。引いたくじをもとに戻さないで、A,B,Cの3人がこの順に1本ずつ引くとき、次の問に答えよ。
(1)Cが当たる確率を求めよ。
(2)次の文のうち、正しいものを1つ選べ。
①Aが最も当たりやすい。
②Bが最も当たりやすい。
③Cが当たる確率を求めよ。
④3人とも当たりやすさは同じ。
この動画を見る
10本のくじの中に当たりくじが2本ある。引いたくじをもとに戻さないで、A,B,Cの3人がこの順に1本ずつ引くとき、次の問に答えよ。
(1)Cが当たる確率を求めよ。
(2)次の文のうち、正しいものを1つ選べ。
①Aが最も当たりやすい。
②Bが最も当たりやすい。
③Cが当たる確率を求めよ。
④3人とも当たりやすさは同じ。
