 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【初めの一手は…!】二次方程式:中央大学杉並高等学校~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#高校入試過去問(数学)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$4(x - 7)(x - 16)+56 = (x-8)(x-9)$を解きなさい
この動画を見る
$4(x - 7)(x - 16)+56 = (x-8)(x-9)$を解きなさい
福田のおもしろ数学411〜漸化式で定まる数列の2020項までの和と2030項までの和から2025項までの和を求める

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$\{a_n\}$は$a_n=a_{n-1}-a_{n-2} (n\geqq 3)$を
満たしている。
$\displaystyle \sum_{n=1}^{2020}=2030$ $\quad $ $\displaystyle \sum_{n=1}^{2030}=2020$
を満たすとき
$\displaystyle \sum_{n=1}^{2025} a_n$の値を求めよ。
この動画を見る
数列$\{a_n\}$は$a_n=a_{n-1}-a_{n-2} (n\geqq 3)$を
満たしている。
$\displaystyle \sum_{n=1}^{2020}=2030$ $\quad $ $\displaystyle \sum_{n=1}^{2030}=2020$
を満たすとき
$\displaystyle \sum_{n=1}^{2025} a_n$の値を求めよ。
【数C】【平面上のベクトル】ベクトル方程式1 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1
$\triangle ABC$の重心を$G$、辺$BC$の中点を$M$とし、$\overrightarrow{GA}=\vec{a}, \overrightarrow{GB}=\vec{b}$とする。
(1) $\overrightarrow{AM}$、$\overrightarrow{GC}$を$\vec{a}, \vec{b}$を用いて表せ。
(2)点$M$を通り、辺$CA$に平行な直線上の点を$P$とし、$\overrightarrow{GP}=\vec{p}$とする。この直線のベクトル方程式を、$\vec{a}, \vec{b}, \vec{p}$を用いて求めよ。
問題2
2直線 $l:(x,y)=(0,3)+s(1,2), m:(x,y)=(6,1)+t(-2,3)$について、次の問いに答えよ。ただし、$s,t$は媒介変数とする。
(1)$l$と$m$の交点の座標を求めよ。
(2)点$P(4,1)$から$l$に垂線$PQ$を下ろす。このとき、点$Q$の座標を求めよ。
問題3
$\triangle OAB$に対して、点$P$が次の条件を満たしながら動くとき、点$P$の存在範囲を図示せよ。
(1) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}, s+t=4, s\geqq0, t\geqq0$
(2) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}, 0\leqq s+t\leqq4, s\geqq0, t\geqq0$
この動画を見る
問題1
$\triangle ABC$の重心を$G$、辺$BC$の中点を$M$とし、$\overrightarrow{GA}=\vec{a}, \overrightarrow{GB}=\vec{b}$とする。
(1) $\overrightarrow{AM}$、$\overrightarrow{GC}$を$\vec{a}, \vec{b}$を用いて表せ。
(2)点$M$を通り、辺$CA$に平行な直線上の点を$P$とし、$\overrightarrow{GP}=\vec{p}$とする。この直線のベクトル方程式を、$\vec{a}, \vec{b}, \vec{p}$を用いて求めよ。
問題2
2直線 $l:(x,y)=(0,3)+s(1,2), m:(x,y)=(6,1)+t(-2,3)$について、次の問いに答えよ。ただし、$s,t$は媒介変数とする。
(1)$l$と$m$の交点の座標を求めよ。
(2)点$P(4,1)$から$l$に垂線$PQ$を下ろす。このとき、点$Q$の座標を求めよ。
問題3
$\triangle OAB$に対して、点$P$が次の条件を満たしながら動くとき、点$P$の存在範囲を図示せよ。
(1) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}, s+t=4, s\geqq0, t\geqq0$
(2) $\overrightarrow{OP}=s\overrightarrow{OA}+t\overrightarrow{OB}, 0\leqq s+t\leqq4, s\geqq0, t\geqq0$
【数C】【平面上のベクトル】ベクトルと図形3 ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1
$\triangle \rm{ABC}$において、$\rm{AB}=3,AC=2, \angle A=60^{ \circ }$,外心を$\rm{O}$とする。$\overrightarrow{{\textrm{AB}}}=\vec{b},\overrightarrow{{\textrm{AC}}}=\vec{c}$とするとき、$\overrightarrow{{\textrm{AO}}}$を$\vec{b},\vec{c}$を用いて表せ。
問題2
平行四辺形$\rm{ABCD}$において、次の等式が成り立つことを証明せよ。
$\rm{2(AB^2+BC^2)=AC^2+BD^2}$
問題3
$\triangle \rm{ABC}$の辺$\rm{BC}$を1:2に内分する点を$\rm{D}$とする。このとき、等式$\rm{2AB^2+AC^2=3(AD^2+2BD^2)}$が成り立つことを証明せよ。
この動画を見る
問題1
$\triangle \rm{ABC}$において、$\rm{AB}=3,AC=2, \angle A=60^{ \circ }$,外心を$\rm{O}$とする。$\overrightarrow{{\textrm{AB}}}=\vec{b},\overrightarrow{{\textrm{AC}}}=\vec{c}$とするとき、$\overrightarrow{{\textrm{AO}}}$を$\vec{b},\vec{c}$を用いて表せ。
問題2
平行四辺形$\rm{ABCD}$において、次の等式が成り立つことを証明せよ。
$\rm{2(AB^2+BC^2)=AC^2+BD^2}$
問題3
$\triangle \rm{ABC}$の辺$\rm{BC}$を1:2に内分する点を$\rm{D}$とする。このとき、等式$\rm{2AB^2+AC^2=3(AD^2+2BD^2)}$が成り立つことを証明せよ。
【数C】【平面上のベクトル】位置ベクトル ※問題文は概要欄

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1
$\triangle \rm{ABC}$の重心を$\rm{G}$とするとき、この平面上の任意の点$\rm{P}$に対して、等式$\rm{\overrightarrow{AP}+\overrightarrow{BP}-2\overrightarrow{CP}=3\overrightarrow{GC}}$が成り立つことを証明せよ。
問題2
$\triangle \rm{ABC}$と点$\rm{P}$に対して、次の等式が成り立つとき、点$\rm{P}$の位置をいえ。
(1) $\rm{\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{AB}}$
(2)$\rm{\overrightarrow{AP}+\overrightarrow{BP}+\overrightarrow{CP}=\vec{0}} $
(3)$\rm{\overrightarrow{PA}+\overrightarrow{PC}=\overrightarrow{AC}}$
問題3
$\triangle \rm{ABC}$と点$\rm{P}$に対して、等式 $\rm{5\overrightarrow{AP}+4\overrightarrow{BP}+3\overrightarrow{CP}=\vec{0}}$が成り立っている。
(1)点$\rm{P}$の位置をいえ。
(2)$\triangle \rm{PBC}:\triangle \rm{PCA}:\triangle \rm{PAB}$を求めよ。
この動画を見る
問題1
$\triangle \rm{ABC}$の重心を$\rm{G}$とするとき、この平面上の任意の点$\rm{P}$に対して、等式$\rm{\overrightarrow{AP}+\overrightarrow{BP}-2\overrightarrow{CP}=3\overrightarrow{GC}}$が成り立つことを証明せよ。
問題2
$\triangle \rm{ABC}$と点$\rm{P}$に対して、次の等式が成り立つとき、点$\rm{P}$の位置をいえ。
(1) $\rm{\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}=\overrightarrow{AB}}$
(2)$\rm{\overrightarrow{AP}+\overrightarrow{BP}+\overrightarrow{CP}=\vec{0}} $
(3)$\rm{\overrightarrow{PA}+\overrightarrow{PC}=\overrightarrow{AC}}$
問題3
$\triangle \rm{ABC}$と点$\rm{P}$に対して、等式 $\rm{5\overrightarrow{AP}+4\overrightarrow{BP}+3\overrightarrow{CP}=\vec{0}}$が成り立っている。
(1)点$\rm{P}$の位置をいえ。
(2)$\triangle \rm{PBC}:\triangle \rm{PCA}:\triangle \rm{PAB}$を求めよ。
【数Ⅲ】【微分とその応用】n次導関数と微分の表し方 ※問題文は概要欄

単元:
#微分とその応用#微分法#色々な関数の導関数#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数について, $\frac{ dy }{ dx }$ を求めよ。ただし (1)(2)では $y$ を用いて表してもよい。また(3)(4)では、t$$ の関数として表せ。$a,b$は正の定数とする。
$x²+3xy-y²=1$
$x$の関数 $y$ が、$t$ を媒介変数として $x=cost +tsint, y= sint - tcost$ と表せるとき、$\frac{ d^2 y }{ dx^2 }$ を$ t $の関数として表せ。
この動画を見る
次の関数について, $\frac{ dy }{ dx }$ を求めよ。ただし (1)(2)では $y$ を用いて表してもよい。また(3)(4)では、t$$ の関数として表せ。$a,b$は正の定数とする。
$x²+3xy-y²=1$
$x$の関数 $y$ が、$t$ を媒介変数として $x=cost +tsint, y= sint - tcost$ と表せるとき、$\frac{ d^2 y }{ dx^2 }$ を$ t $の関数として表せ。
【数Ⅲ】【微分とその応用】導関数の応用1 ※問題文は概要欄

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
媒介変数$ t $で表された次の曲線について、( )内の$ t$ の値に対応する点における接線の方程式を求めよ。
$x= \sqrt{ 3 } cost ⋂ y= sint (t=π/6)$
次の曲線について、与えられた点を通る接線の方程式を求めよ。
$y = \sqrt{ x } (-2,0)$
曲線$ y= e^x + 2e^{-x}$において、傾きが$1$である接線の方程式を求めよ。
この動画を見る
媒介変数$ t $で表された次の曲線について、( )内の$ t$ の値に対応する点における接線の方程式を求めよ。
$x= \sqrt{ 3 } cost ⋂ y= sint (t=π/6)$
次の曲線について、与えられた点を通る接線の方程式を求めよ。
$y = \sqrt{ x } (-2,0)$
曲線$ y= e^x + 2e^{-x}$において、傾きが$1$である接線の方程式を求めよ。
福田のおもしろ数学410〜条件を満たすKの最大値

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の貢献を満たす実数$k$の最大値は?
「$a+b+c\leqq K$を満たす任意の正の実数
$a,b,c$に対して$abc \leqq K$が成り立つ」
この動画を見る
次の貢献を満たす実数$k$の最大値は?
「$a+b+c\leqq K$を満たす任意の正の実数
$a,b,c$に対して$abc \leqq K$が成り立つ」
【数Ⅲ】【微分とその応用】n次導関数基本 ※問題文は概要欄

単元:
#微分とその応用#微分法#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数の第3次導関数を求めよ。
y= √ (2x+1)
以下、略
次のことが成り立つことを証明せよ。
y= x√ (1+x²)のとき、(1+x²)y'' + xy' = 4y
以下、略
この動画を見る
次の関数の第3次導関数を求めよ。
y= √ (2x+1)
以下、略
次のことが成り立つことを証明せよ。
y= x√ (1+x²)のとき、(1+x²)y'' + xy' = 4y
以下、略
【数Ⅲ】【微分とその応用】色々な関数の微分2 ※問題文は概要欄

単元:
#微分とその応用#色々な関数の導関数#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
対数微分法により次の関数を微分せよ。ただし、aは定数とする。
y= (x+1)²/((x+2)³(x+3)⁴)
以下、略
次の関数を微分せよ。ただし x>0 とする。
y= x^sinx
以下、略
lim_(k→0) (1+k)^(1/k)=e を用いて、次の極限を求めよ。
lim_(x→0) ((log(1+x)/x)
以下、略
この動画を見る
対数微分法により次の関数を微分せよ。ただし、aは定数とする。
y= (x+1)²/((x+2)³(x+3)⁴)
以下、略
次の関数を微分せよ。ただし x>0 とする。
y= x^sinx
以下、略
lim_(k→0) (1+k)^(1/k)=e を用いて、次の極限を求めよ。
lim_(x→0) ((log(1+x)/x)
以下、略
【スッキリ理解できる…!】一次関数:駿台甲府高等学校~全国入試問題解法
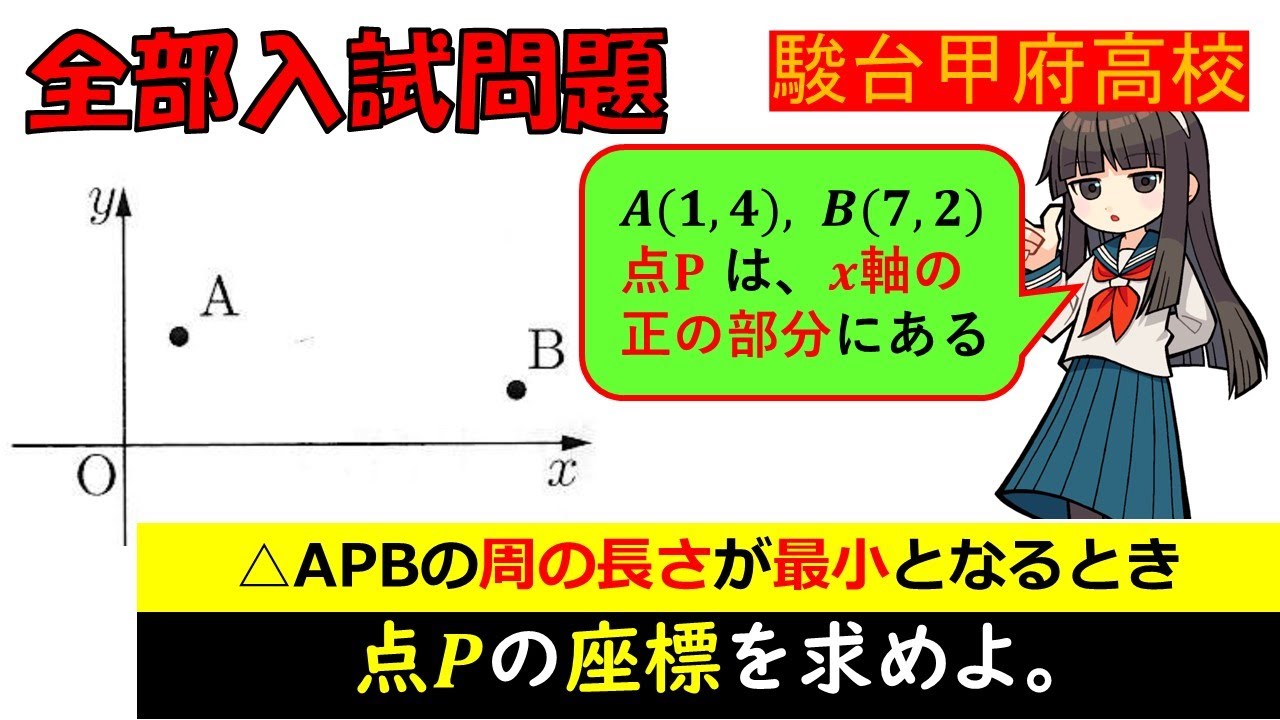
単元:
#図形と計量#平面図形#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2点$A = (1.4) B = (7.2)$で、$点Pは正の所を動く。$$\triangle APB$の周の長さが最小となるとき点$P$の座標を求めよ
この動画を見る
2点$A = (1.4) B = (7.2)$で、$点Pは正の所を動く。$$\triangle APB$の周の長さが最小となるとき点$P$の座標を求めよ
【数A】【図形の性質】円に内接する図形 ※問題文は概要欄

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
円oにおいて、平行な2つの弦をAA´、BB´とし、AB´とA´Bが円の内部の点Pで交わっている。このとき、∠APB=∠AOBであることを証明せよ。
鋭角三角形ABCの垂心をHとし、AHがBCと交わる点をD、△ABCの外接円と交わる点をEとする。このとき、Dは線分HEの中点であることを証明せよ。
下の図において、角θを求めよ。
この動画を見る
円oにおいて、平行な2つの弦をAA´、BB´とし、AB´とA´Bが円の内部の点Pで交わっている。このとき、∠APB=∠AOBであることを証明せよ。
鋭角三角形ABCの垂心をHとし、AHがBCと交わる点をD、△ABCの外接円と交わる点をEとする。このとき、Dは線分HEの中点であることを証明せよ。
下の図において、角θを求めよ。
【数A】【図形の性質】三角形の関係証明 ※問題文は概要欄

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
△ABCの内部の1点をPとするとき、AP+BP+CP>1/2(AB+BC+CA)を証明せよ。
上の図において、点Pが線分CD上を動くとき、線分の和AP+PBの最小値とそのときの点Pの位置を求めよ。
この動画を見る
△ABCの内部の1点をPとするとき、AP+BP+CP>1/2(AB+BC+CA)を証明せよ。
上の図において、点Pが線分CD上を動くとき、線分の和AP+PBの最小値とそのときの点Pの位置を求めよ。
【数A】【図形の性質】三角形の辺と角 ※問題文は概要欄

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
∠B=90度の直角三角形ABCの辺BC上に頂点と異なる点Pを取る時、AB<AP<ACであることを証明せよ。
△ABCにおいて、AB>ACとする。∠Aの二等分線と辺BCの交点をPとする時、次の①~④のうちで常に成り立つものを全て選べ。
①BP=PC ②AB>AP ③AC>AP ④AC>CP
次の長さの線分を3辺とする三角形が存在するようなXの値の範囲を求めよ。
(1)X、2、6 (2)3X、X+4、X+2
この動画を見る
∠B=90度の直角三角形ABCの辺BC上に頂点と異なる点Pを取る時、AB<AP<ACであることを証明せよ。
△ABCにおいて、AB>ACとする。∠Aの二等分線と辺BCの交点をPとする時、次の①~④のうちで常に成り立つものを全て選べ。
①BP=PC ②AB>AP ③AC>AP ④AC>CP
次の長さの線分を3辺とする三角形が存在するようなXの値の範囲を求めよ。
(1)X、2、6 (2)3X、X+4、X+2
【数A】【図形の性質】チェバメネラウス ※問題文は概要欄

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1):△ABCの辺AB、AC上に、それぞれ頂点と異なる点D、Eを取る時、等式【△ADE/△ABC】=【AD/AB】×【AE/AC】が成り立つことを証明せよ。
(2):△ABCの辺BCを2:3、辺CAを3:1、辺ABを1:2に内分する点をそれぞれD、E、Fとする時、次の値を求めよ。
(ア)△AFE/△ABC (イ)△DEF/△ABC
△ABCの辺ABを2:3に内分する点をR、辺ACを5:6に内分する点をQとする。線分BQと線分CRの交点をOとする。直線AOと辺BCの交点をPとする。
(1)BP:PCを求めよ。 (2)△OBC:△ABCを求めよ。
△ABCの辺ABを2:1に内分する点をD、辺ACを3:1に内分する点をEとする。直線DEとBCの交点をPとする。
(1)BP:PCを求めよ。 (2)DP:PEを求めよ。
この動画を見る
(1):△ABCの辺AB、AC上に、それぞれ頂点と異なる点D、Eを取る時、等式【△ADE/△ABC】=【AD/AB】×【AE/AC】が成り立つことを証明せよ。
(2):△ABCの辺BCを2:3、辺CAを3:1、辺ABを1:2に内分する点をそれぞれD、E、Fとする時、次の値を求めよ。
(ア)△AFE/△ABC (イ)△DEF/△ABC
△ABCの辺ABを2:3に内分する点をR、辺ACを5:6に内分する点をQとする。線分BQと線分CRの交点をOとする。直線AOと辺BCの交点をPとする。
(1)BP:PCを求めよ。 (2)△OBC:△ABCを求めよ。
△ABCの辺ABを2:1に内分する点をD、辺ACを3:1に内分する点をEとする。直線DEとBCの交点をPとする。
(1)BP:PCを求めよ。 (2)DP:PEを求めよ。
【数A】【図形の性質】図形の性質の基本2 ※問題文は概要欄

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形ABCの内心をIとし、3辺BC、CA、ABに関してIと対称な点をそれぞれP,Q,Rとする。Iは三角形PQRについてどのような点か?
三角形ABCの内心をI、角Aの内部の傍心をI₁とする時、次の問いに答えよ。
(1)角IBI₁の大きさを求めよ。
(2)三角形ABCの外接円は線分II₁を二等分することを証明せよ。
AB=ACである二等辺三角形ABCの頂点Aから辺BCに下ろした垂線をADとする。
角Bの内部の傍接円IBの半径はADに等しいことを証明せよ。
この動画を見る
三角形ABCの内心をIとし、3辺BC、CA、ABに関してIと対称な点をそれぞれP,Q,Rとする。Iは三角形PQRについてどのような点か?
三角形ABCの内心をI、角Aの内部の傍心をI₁とする時、次の問いに答えよ。
(1)角IBI₁の大きさを求めよ。
(2)三角形ABCの外接円は線分II₁を二等分することを証明せよ。
AB=ACである二等辺三角形ABCの頂点Aから辺BCに下ろした垂線をADとする。
角Bの内部の傍接円IBの半径はADに等しいことを証明せよ。
【数A】【図形の性質】図形の性質の基本1 ※問題文は概要欄

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
外心と内心が一致する三角形は正三角形である。このことを証明せよ。
図の三角形ABCは角B=90度の直角三角形であり、3点D、E、Fは三角形ABCの外心・内心・重心のいずれかであるとする。このとき、三角形ABCの外心・内心・重心は3点D、E、Fのいずれであるか?
三角形ABCにおいて、AB=AC=3、BC=2である。三角形ABCの重心をG、内心をIとするとき、線分GIの長さを求めよ。
図において、点Hは三角形ABCの垂心である。角α、βを求めよ。
この動画を見る
外心と内心が一致する三角形は正三角形である。このことを証明せよ。
図の三角形ABCは角B=90度の直角三角形であり、3点D、E、Fは三角形ABCの外心・内心・重心のいずれかであるとする。このとき、三角形ABCの外心・内心・重心は3点D、E、Fのいずれであるか?
三角形ABCにおいて、AB=AC=3、BC=2である。三角形ABCの重心をG、内心をIとするとき、線分GIの長さを求めよ。
図において、点Hは三角形ABCの垂心である。角α、βを求めよ。
福田のおもしろ数学408〜変数が素数である連立方程式

単元:
#連立方程式#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
pq=r+1 \\
2(p^2+q^2)=r^2+1
\end{array}
\right.
\end{eqnarray}$
を満たす素数$p,q,r$を求めて下さい。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
pq=r+1 \\
2(p^2+q^2)=r^2+1
\end{array}
\right.
\end{eqnarray}$
を満たす素数$p,q,r$を求めて下さい。
【数A】【場合の数と確率】組み合わせ応用3 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
・右のような街路で、PからQまで行く最短経路のうち、次の場合は何通りあるか。
(1)総数
(2)Rを通る経路
(3)R、Sをともに通る経路
(4)×印の個所を通らない経路
・4桁の自然数nの千の位、百の位、十の位、一の位の数字を、それぞれa,b,c,dとする。次の条件を満たすnは全部で何個あるか。
(1)a>b>c>d
(2)a≧b>c>d
この動画を見る
・右のような街路で、PからQまで行く最短経路のうち、次の場合は何通りあるか。
(1)総数
(2)Rを通る経路
(3)R、Sをともに通る経路
(4)×印の個所を通らない経路
・4桁の自然数nの千の位、百の位、十の位、一の位の数字を、それぞれa,b,c,dとする。次の条件を満たすnは全部で何個あるか。
(1)a>b>c>d
(2)a≧b>c>d
【数A】【場合の数と確率】組み合わせ応用2 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
・円に内接する八角形の3個の頂点を結んで三角形を作る。
(1)八角形と一辺だけを共有する三角形は何個あるか。
(2)八角形と辺を共有しない三角形は何個あるか。
・1から20までの20個の整数から、異なる3個を選んで組を作る。
(1)奇数だけを含んでいる組は何通りできるか。
(2)奇数も偶数も含んでいる組は何通りできるか。
(3)3個の数の和が奇数となる組は何通りできるか。
この動画を見る
・円に内接する八角形の3個の頂点を結んで三角形を作る。
(1)八角形と一辺だけを共有する三角形は何個あるか。
(2)八角形と辺を共有しない三角形は何個あるか。
・1から20までの20個の整数から、異なる3個を選んで組を作る。
(1)奇数だけを含んでいる組は何通りできるか。
(2)奇数も偶数も含んでいる組は何通りできるか。
(3)3個の数の和が奇数となる組は何通りできるか。
【数A】【場合の数と確率】組み合わせ応用1 ※問題文は概要欄 ※解答に誤りあり(概要欄に記載しています)

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
・4個の数字0,1,2,3を使ってできる次のような自然数は何個あるか。ただし、同じ数字を重複して使ってよいものとする。
(1)3桁の自然数
(2)3桁以下の自然数
(3)123より小さい自然数
・9個の要素を持つ集合の総数を求めよ。また、Aの2個の特定の要素を含むAの部分集合の総数を求めよ。
・(1)10人を2つの部屋A,Bに入れる方法は何通りあるか。ただし10人全員が同じ部屋に入ってもよいものとする。
(2)10人を二つの組A,Bに分ける方法は何通りあるか。
(3)10人を二つの組に分ける方法は何通りあるか。
この動画を見る
・4個の数字0,1,2,3を使ってできる次のような自然数は何個あるか。ただし、同じ数字を重複して使ってよいものとする。
(1)3桁の自然数
(2)3桁以下の自然数
(3)123より小さい自然数
・9個の要素を持つ集合の総数を求めよ。また、Aの2個の特定の要素を含むAの部分集合の総数を求めよ。
・(1)10人を2つの部屋A,Bに入れる方法は何通りあるか。ただし10人全員が同じ部屋に入ってもよいものとする。
(2)10人を二つの組A,Bに分ける方法は何通りあるか。
(3)10人を二つの組に分ける方法は何通りあるか。
【数A】【場合の数と確率】塗分け ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
・色の異なる7個の玉をつないで首飾りにする方法は何通りあるか。
・正三角柱の5つの面を青、白、赤、黄、緑の5色すべてを使って塗分ける方法は何通りあるか。
この動画を見る
・色の異なる7個の玉をつないで首飾りにする方法は何通りあるか。
・正三角柱の5つの面を青、白、赤、黄、緑の5色すべてを使って塗分ける方法は何通りあるか。
【数A】【場合の数と確率】円順列基本 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
・大人2人と子供8人が円形のテーブルに着席するとき、次のような並び方は何通りあるか。
(1)大人2人が隣り合う。
(2)大人2人が向かい合う。
・男子4人、女子4人が手をつないで輪を作るとき、次のような並び方は何通りあるか。
(1)女子4人が続いて並ぶ。
(2)男女が交互に並ぶ。
・8人の中から選ばれた5人が円形上に並ぶとき、並び方は何通りあるか。
この動画を見る
・大人2人と子供8人が円形のテーブルに着席するとき、次のような並び方は何通りあるか。
(1)大人2人が隣り合う。
(2)大人2人が向かい合う。
・男子4人、女子4人が手をつないで輪を作るとき、次のような並び方は何通りあるか。
(1)女子4人が続いて並ぶ。
(2)男女が交互に並ぶ。
・8人の中から選ばれた5人が円形上に並ぶとき、並び方は何通りあるか。
【数A】【場合の数と確率】並び替え基本2 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
・「equations」という単語の文字をすべて使って順列を作るとき、次の問いに答えよ。
(1)少なくとも一端に子音の文字がくるものは何通りあるか。
(2)eとaの間に文字が2つあるものは何通りあるか。
・A,B,C,D,E,Fの6文字をすべて使ってできる順列を、ABCDEFを1番目として自書式に並べるとき、次の問いに答えよ。
(1)140番目の文字列を求めよ。
(2)FBCDAEは何番目の文字列か。
この動画を見る
・「equations」という単語の文字をすべて使って順列を作るとき、次の問いに答えよ。
(1)少なくとも一端に子音の文字がくるものは何通りあるか。
(2)eとaの間に文字が2つあるものは何通りあるか。
・A,B,C,D,E,Fの6文字をすべて使ってできる順列を、ABCDEFを1番目として自書式に並べるとき、次の問いに答えよ。
(1)140番目の文字列を求めよ。
(2)FBCDAEは何番目の文字列か。
【数A】【場合の数と確率】並び替え基本1 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
・6個の数字1,2,3,4,5,6から異なる4種の数字を使って4桁の整数を作るとき、次のような整数は何個あるか。
(1)4300より大きい整数
(2)5000より大きい整数
・女子5人、男子3人が1列に並ぶとき、次の並び方は何通りあるか。
(1)女子5人が続いて並ぶ。
(2)女子5人、男子3人がそれぞれ続いて並ぶ。
(3)両端が男子である。
(4)どの男子も隣合わない。
・男子4人、女子4人が男女交互に1列に並ぶ方法は何通りあるか。
この動画を見る
・6個の数字1,2,3,4,5,6から異なる4種の数字を使って4桁の整数を作るとき、次のような整数は何個あるか。
(1)4300より大きい整数
(2)5000より大きい整数
・女子5人、男子3人が1列に並ぶとき、次の並び方は何通りあるか。
(1)女子5人が続いて並ぶ。
(2)女子5人、男子3人がそれぞれ続いて並ぶ。
(3)両端が男子である。
(4)どの男子も隣合わない。
・男子4人、女子4人が男女交互に1列に並ぶ方法は何通りあるか。
【数A】【場合の数と確率】組み合わせ考え方の基本 ※問題文は概要欄

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#場合の数と確率#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
・5人乗りの車に5人が乗車してドライブをするとき、乗り方は何通りあるか。次の各場合について求めよ。
(1)5人全員が運転免許を持っている場合
(2)5人のうち3人だけが運転免許を持っている場合
・6個の数字0,1,2,3,4,5を使ってできる、次のような整数は何個あるか。ただし、同じ数字は2度以上使わないこととする。
(1)6桁の整数
(2)6桁の整数で5の倍数
・5個の数字0,1,2,3,4を使ってできる3桁の整数のうち、次のような整数は何個あるか。ただし、同じ数字は2度以上使わないものとする。
(1)偶数
(2)3の倍数
この動画を見る
・5人乗りの車に5人が乗車してドライブをするとき、乗り方は何通りあるか。次の各場合について求めよ。
(1)5人全員が運転免許を持っている場合
(2)5人のうち3人だけが運転免許を持っている場合
・6個の数字0,1,2,3,4,5を使ってできる、次のような整数は何個あるか。ただし、同じ数字は2度以上使わないこととする。
(1)6桁の整数
(2)6桁の整数で5の倍数
・5個の数字0,1,2,3,4を使ってできる3桁の整数のうち、次のような整数は何個あるか。ただし、同じ数字は2度以上使わないものとする。
(1)偶数
(2)3の倍数
数学的に「悪魔の証明」をやる方法を数学者に聞いてみた

【入試で必要な発想…!】図形:明治学院高等学校~全国入試問題解法
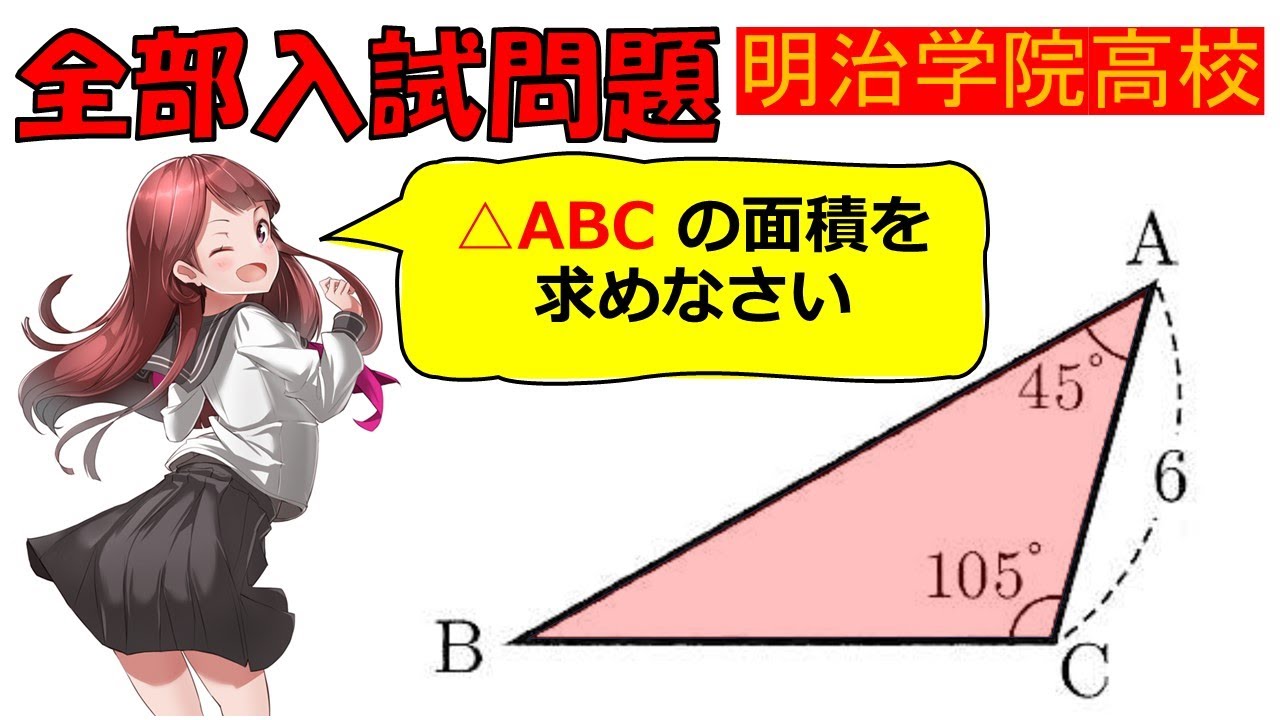
単元:
#数学(中学生)#数Ⅰ#図形と計量#平面図形#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\triangleABCの面積を求めなさい$
この動画を見る
$\triangleABCの面積を求めなさい$
大学受験生が覚えてたら差がつく公式

福田のおもしろ数学407〜a^3+b^3+c^3-3abcの取り得る最小の正の値

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の整数$a,b,c$に対して
$a^3+b^3+c^3-3abc$
が取り得る最小の正の値を求めよ。
またそのときの$a,b,c$の値は?
この動画を見る
正の整数$a,b,c$に対して
$a^3+b^3+c^3-3abc$
が取り得る最小の正の値を求めよ。
またそのときの$a,b,c$の値は?
