 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
ただの4次方程式 その2

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$x^4+2x^2-400x=9991$
この動画を見る
これを解け.
$x^4+2x^2-400x=9991$
数列の和 解説2通り!!
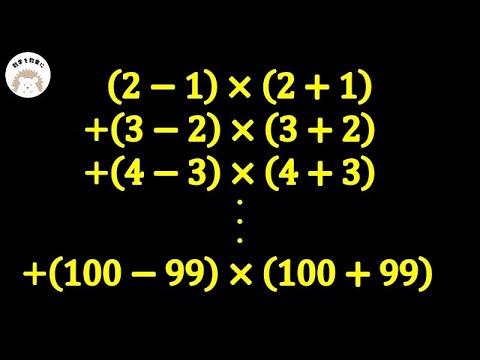
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$(2-1) \times (2+1) + (3-2)(3+2)+(4-3)(4+3)+ \cdots +(99-98)(99+98)+(100-99)(100+99)$
この動画を見る
$(2-1) \times (2+1) + (3-2)(3+2)+(4-3)(4+3)+ \cdots +(99-98)(99+98)+(100-99)(100+99)$
数学「大学入試良問集」【10−5① 直線の通過領域の基礎】を宇宙一わかりやすく

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の条件をみたす直線の通過領域を図示せよ。
(1)実数$t$が$0 \lt t \lt 1$をみたすときの直線$y=t(x-2)+3$の通過領域
(2)$t$が実数全体を動くときの直線$y=tx+t^2$の通過領域
この動画を見る
次の条件をみたす直線の通過領域を図示せよ。
(1)実数$t$が$0 \lt t \lt 1$をみたすときの直線$y=t(x-2)+3$の通過領域
(2)$t$が実数全体を動くときの直線$y=tx+t^2$の通過領域
因数分解 京都産業大学

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x^2-2x)^2-2x^2+4x-3$を因数分解せよ。
京都産業大学
この動画を見る
$(x^2-2x)^2-2x^2+4x-3$を因数分解せよ。
京都産業大学
福田のわかった数学〜高校3年生理系001〜極限(1)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(1)
$\displaystyle\lim_{n \to \infty}\displaystyle \frac{a_n+3}{a_n+1}=2$のとき
$\displaystyle\lim_{n \to \infty}a_n$を求めよ。
この動画を見る
数学$\textrm{III}$ 極限(1)
$\displaystyle\lim_{n \to \infty}\displaystyle \frac{a_n+3}{a_n+1}=2$のとき
$\displaystyle\lim_{n \to \infty}a_n$を求めよ。
【数B・Ⅲ】漸化式と極限:連立漸化式:数列{x[n]},{y[n]}をx[1]=y[1]=1, x[n+1]=(2/3)x[n]+(1/6)y[n], y[n+1]=(1/3)x[n]+(5/6)y…

単元:
#数列#漸化式#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
数列{$x_n$},{$y_n$}を$x_1=y_1=1, x_{n+1}=\dfrac{2}{3}x_n+\dfrac{1}{6}y_n, y_{n+1}=\dfrac{1}{3}x_n+\dfrac{5}{6}y_n$で定めるとき、
(1)$x_{n+1}+αy_{n+1}=\beta(x_n+αy_n)$を満たす$\alpha,\beta$の組を2組求めよう。
(2)数列{$x_n$},{$y_n$}の一般項を求めよう。
(3)数列{$x_n$},{$y_n$}の極限を求めよう。
この動画を見る
数列{$x_n$},{$y_n$}を$x_1=y_1=1, x_{n+1}=\dfrac{2}{3}x_n+\dfrac{1}{6}y_n, y_{n+1}=\dfrac{1}{3}x_n+\dfrac{5}{6}y_n$で定めるとき、
(1)$x_{n+1}+αy_{n+1}=\beta(x_n+αy_n)$を満たす$\alpha,\beta$の組を2組求めよう。
(2)数列{$x_n$},{$y_n$}の一般項を求めよう。
(3)数列{$x_n$},{$y_n$}の極限を求めよう。
福田のわかった数学〜高校2年生第7回〜2変数関数の最大最小

単元:
#数Ⅱ#式と証明#微分法と積分法#恒等式・等式・不等式の証明#平均変化率・極限・導関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 2変数関数の最大最小
$x,y$が$0 \leqq x \leqq 1,0 \leqq y \leqq 1$を
満たして変化するときの2変数関数
$f(x,y)=5xy-2(x+y)+1$
の最大値$M,$最小値$m$を求めよ。
この動画を見る
数学$\textrm{II}$ 2変数関数の最大最小
$x,y$が$0 \leqq x \leqq 1,0 \leqq y \leqq 1$を
満たして変化するときの2変数関数
$f(x,y)=5xy-2(x+y)+1$
の最大値$M,$最小値$m$を求めよ。
06愛知県教員採用試験(数学:8-(1) 極限)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{8}-(1)$
$\displaystyle \lim_{x\to 0} \dfrac{\tan x-\sin x}{x^3}$を求めよ.
この動画を見る
$\boxed{8}-(1)$
$\displaystyle \lim_{x\to 0} \dfrac{\tan x-\sin x}{x^3}$を求めよ.
ただの4次方程式
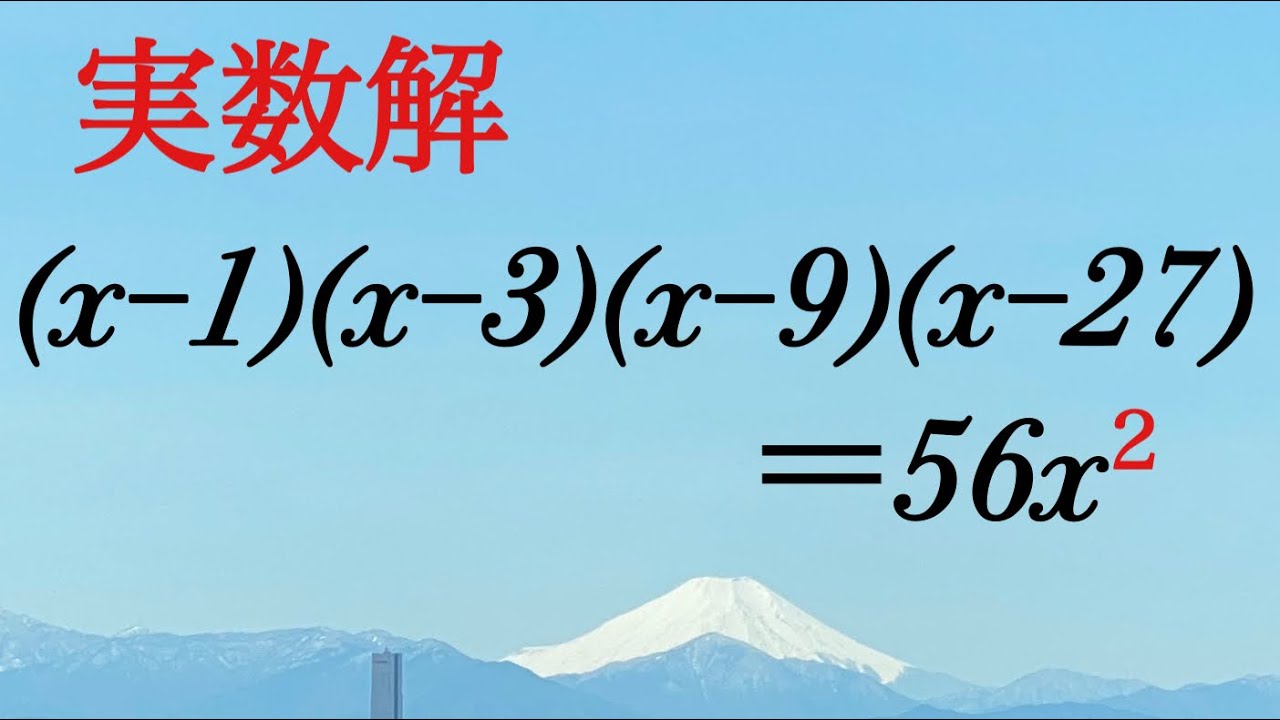
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$(x-1)(x-3)(x-9)(x-27)=56x^2$
この動画を見る
実数解を求めよ.
$(x-1)(x-3)(x-9)(x-27)=56x^2$
指数の計算 穴埋め
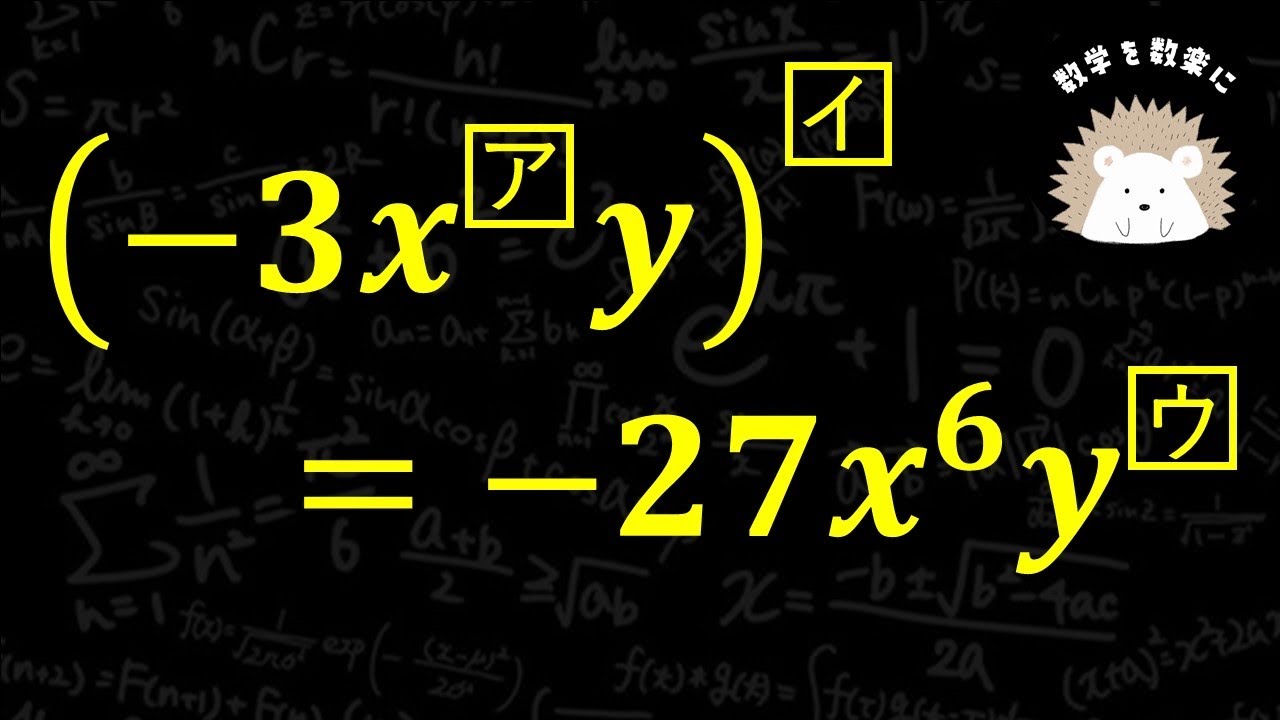
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(-3x^{ \boxed{ア}}y)^{ \boxed{イ}} = -27x^6y^{ \boxed{ウ}}$
この動画を見る
$(-3x^{ \boxed{ア}}y)^{ \boxed{イ}} = -27x^6y^{ \boxed{ウ}}$
数学「大学入試良問集」【10−4 α+βとαβの軌跡】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#岐阜大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
点$P(\alpha,\beta)$が$\alpha^2+\beta^2+\alpha\beta \lt 1$をみたして動くとき、点$Q(\alpha+\beta,\alpha\beta)$の動く範囲を図示せよ。
この動画を見る
点$P(\alpha,\beta)$が$\alpha^2+\beta^2+\alpha\beta \lt 1$をみたして動くとき、点$Q(\alpha+\beta,\alpha\beta)$の動く範囲を図示せよ。
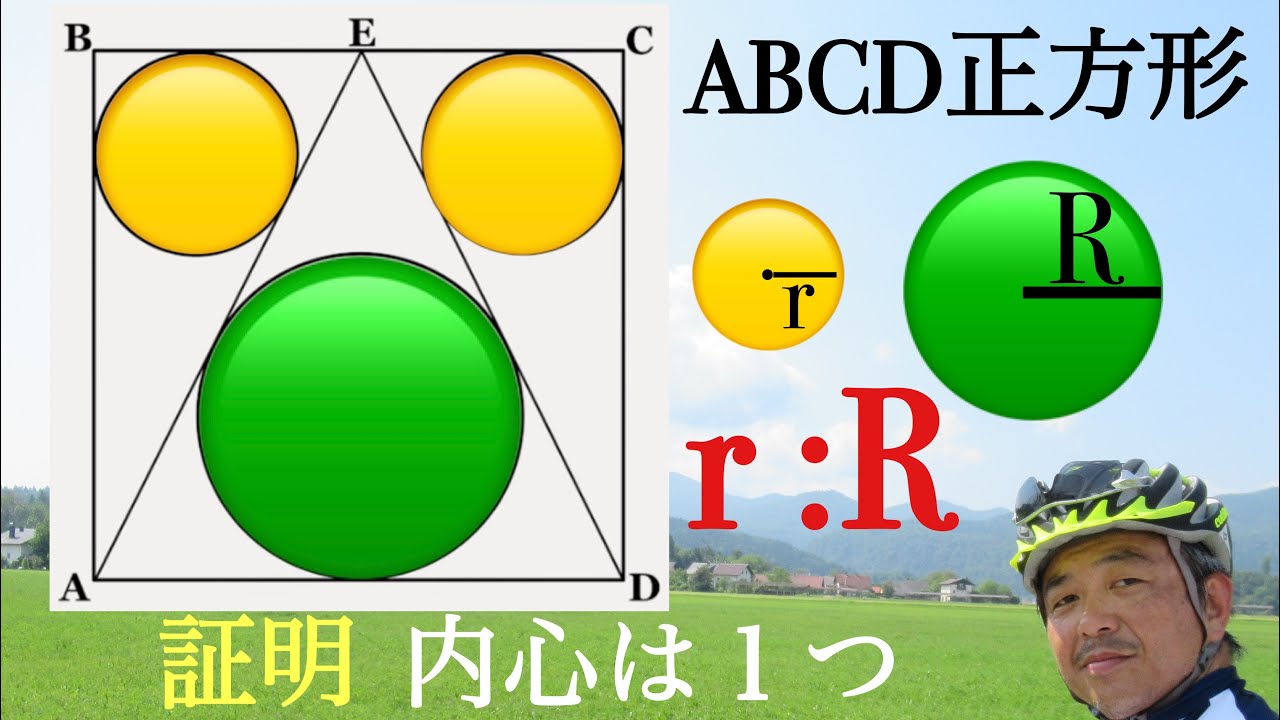
太陽と黒点

単元:
#数A#図形の性質#方べきの定理と2つの円の関係#平面図形#角度と面積#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2つの円の半径の和=47,2つの円の半径の差=43のとき
斜線部の面積=?
*図は動画内参照
この動画を見る
2つの円の半径の和=47,2つの円の半径の差=43のとき
斜線部の面積=?
*図は動画内参照
福田のわかった数学〜高校1年生第7回〜絶対値(第3回)

単元:
#数Ⅰ#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 絶対値(第3回)
次の不等式を解け。
$|x+2|+|2x-1| \lt 4 $
この動画を見る
数学$\textrm{I}$ 絶対値(第3回)
次の不等式を解け。
$|x+2|+|2x-1| \lt 4 $
06愛知県教員採用試験(数学8-(2) 極限)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{8}-(2)$
$\displaystyle \lim_{x\to\infty} \ x\log \left(1+\dfrac{3}{x}\right)$を求めよ.
この動画を見る
$\boxed{8}-(2)$
$\displaystyle \lim_{x\to\infty} \ x\log \left(1+\dfrac{3}{x}\right)$を求めよ.
内心 こんなところに黄金比が
【数B】数列:2以上の自然数に対して、y=x²,y=-x²+2nxで囲まれる部分に含まれる格子点の個数をnの式で表そう。ただし、境界線も含む。

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2以上の自然数に対して、$y=x^2,y=-x^2+2nx$で囲まれる部分に含まれる格子点の個数をnの式で表そう。ただし、境界線も含む。
この動画を見る
2以上の自然数に対して、$y=x^2,y=-x^2+2nx$で囲まれる部分に含まれる格子点の個数をnの式で表そう。ただし、境界線も含む。
数学「大学入試良問集」【10−3 極線と軌跡】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
原点$O$を中心とし、半径1の円を$C$とする。
次の各問いに答えよ。
(1)
直線$y=2$上の点$P(t,2)$から円$C$に2本の接線を引き、その接点を$M,N$とする。
直線$OP$と弦$MN$の交点を$Q$とする。
点$Q$の座標を$t$を用いて表せ。ただし、$t$は実数とする。
(2)
点$P$が直線$y=2$上を動くとき、点$Q$の軌跡を求めよ。
この動画を見る
原点$O$を中心とし、半径1の円を$C$とする。
次の各問いに答えよ。
(1)
直線$y=2$上の点$P(t,2)$から円$C$に2本の接線を引き、その接点を$M,N$とする。
直線$OP$と弦$MN$の交点を$Q$とする。
点$Q$の座標を$t$を用いて表せ。ただし、$t$は実数とする。
(2)
点$P$が直線$y=2$上を動くとき、点$Q$の軌跡を求めよ。
【理数個別の過去問解説】1996年度東北大学 数学 第3問解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
東北大学(1996年)
xy平面の点$(1,0)$を中心とする半径1の円をCとし、第1象限にあって、x軸とCに接する円C₁を考える。次に、x軸、$C、C_1$で囲まれた部分にあって、x軸とこれら2円に接する円を$C_2$とする。以下同様に、$C_{n+1}(n=1,2,…)$をx軸、$C、C_{n}$で囲まれた部分にあって、これらに接する円とする。
(1)$C_1$の中心の座標をaとするとき、C₁の半径$r_1$をaを用いて表そう。
(2)$C_n$の半径$r_n$をaとnを用いて表そう。
この動画を見る
東北大学(1996年)
xy平面の点$(1,0)$を中心とする半径1の円をCとし、第1象限にあって、x軸とCに接する円C₁を考える。次に、x軸、$C、C_1$で囲まれた部分にあって、x軸とこれら2円に接する円を$C_2$とする。以下同様に、$C_{n+1}(n=1,2,…)$をx軸、$C、C_{n}$で囲まれた部分にあって、これらに接する円とする。
(1)$C_1$の中心の座標をaとするとき、C₁の半径$r_1$をaを用いて表そう。
(2)$C_n$の半径$r_n$をaとnを用いて表そう。
福田のわかった数学〜高校2年生第6回〜相加相乗平均の関係

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 相加相乗平均の関係
$a,b,c$を正の数とする。
(1)$\displaystyle \frac{a+b+c}{3} \geqq \sqrt[3]{abc}$を示せ。
(2)$ab+bc+ca=k$(定数)のとき、$abc$の最大値とその時の$a,b,c$を求めよ。
この動画を見る
数学$\textrm{II}$ 相加相乗平均の関係
$a,b,c$を正の数とする。
(1)$\displaystyle \frac{a+b+c}{3} \geqq \sqrt[3]{abc}$を示せ。
(2)$ab+bc+ca=k$(定数)のとき、$abc$の最大値とその時の$a,b,c$を求めよ。
【数Ⅰ】集合と命題:実数全体を全体集合とし、その部分集合A, B, CをA={x| -3≦x≦5}, B={x| |x|<4}, C={x| k-7≦x≦k+3} (kは定数)とする。

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
実数全体を全体集合とし、その部分集合A, B, Cを$A={x| -3≦x≦5}, B={x| |x|<4}, C={x| k-7≦x≦k+3} $(kは定数)とする。
(1)次の集合を求めよう。
(ア)Bバー
(イ)A∪Bバー
(ウ)A∩Bバー。
(2)A⊂Cとなるkの値の範囲を求めよう。
この動画を見る
実数全体を全体集合とし、その部分集合A, B, Cを$A={x| -3≦x≦5}, B={x| |x|<4}, C={x| k-7≦x≦k+3} $(kは定数)とする。
(1)次の集合を求めよう。
(ア)Bバー
(イ)A∪Bバー
(ウ)A∩Bバー。
(2)A⊂Cとなるkの値の範囲を求めよう。
【数Ⅰ】集合と命題:実数aに対して2つの集合をA={a-1, 4, a²-5a+6},B={1, a²-4, a²-7a+12, 4}とする。A∩B={0, 4}であるとき、aの値を求めよう。

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
実数aに対して2つの集合を$A={a-1, 4, a^2-5a+6},B={1, a^2-4, a^2-7a+12, 4}$とする。$A∩B={0, 4}$であるとき、aの値を求めよう。
この動画を見る
実数aに対して2つの集合を$A={a-1, 4, a^2-5a+6},B={1, a^2-4, a^2-7a+12, 4}$とする。$A∩B={0, 4}$であるとき、aの値を求めよう。
06愛知県教員採用試験(数学:6番 指数)

単元:
#数Ⅱ#複素数と方程式#指数関数と対数関数#整式の除法・分数式・二項定理#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$x$の方程式$4^x-2a\ 2^x+2a^2-a-6=0$が
正負が解を1つずつもつとき,
$a$の値の範囲を求めよ.
この動画を見る
$\boxed{6}$
$x$の方程式$4^x-2a\ 2^x+2a^2-a-6=0$が
正負が解を1つずつもつとき,
$a$の値の範囲を求めよ.
【化学】有機化学:2021年度慶應義塾大学薬学部大問4(2)(3)ラストチャプター

単元:
#化学#有機#酸素を含む脂肪族化合物#芳香族化合物#慶應義塾大学#理科(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2021年度慶應義塾大学薬学部大問4(2)(3)ラストチャプター
化合物Aは、水素原子、炭素原子、酸素原子のみから構成され、ベンゼン環を2個含む分子量500以下のエステルである。0.846gの化合物Aを完全燃焼すると、二酸化炭素2.51gと水0.594gを生じた。化合物Aに水酸化ナトリウム水溶液を加えて加熱し加水分解すると、化合物Bのナトリウム塩と化合物Cが生成した。化合物Bを過マンガン酸カリウムで酸化すると化合物Dが生成した。化合物Dと化合物Eを次々と縮合重合させると、高分子化合物Fが得られ、これは繊維として衣料品に用いられる他、樹脂としてペットボトルの原料となる。
一方、化合物Cに濃硫酸を加え170°Cで加熱したところ、化合物Cおよびその構造異性体H、Iが生成した。化合物Hと化合物Iはシスートランス異性体の関係にあり、化合物 Hはシス形、化合物Iはトランス形である。化合物Cをオゾン分解したところ、化合物Jと化合物Kが得られた。また、化合物 Hをオゾン分解したところ、ベンズアルデヒドと化合物Lが得られた。化合物Jと化合物Lはフェーリング液を還元し赤色沈澱を生成した。化合物Kはフェーリング液を還元しなかったが、ヨードホルム反応は陽性だった。なお、オゾン分解の反応経路を図1に示す。
問2 化合物D、E、Kの化合物名を解答用紙に書きなさい。
問3 化合物A、I、J、Lの構造式を、3ページにある例にならって解答用紙に書きなさい。
この動画を見る
2021年度慶應義塾大学薬学部大問4(2)(3)ラストチャプター
化合物Aは、水素原子、炭素原子、酸素原子のみから構成され、ベンゼン環を2個含む分子量500以下のエステルである。0.846gの化合物Aを完全燃焼すると、二酸化炭素2.51gと水0.594gを生じた。化合物Aに水酸化ナトリウム水溶液を加えて加熱し加水分解すると、化合物Bのナトリウム塩と化合物Cが生成した。化合物Bを過マンガン酸カリウムで酸化すると化合物Dが生成した。化合物Dと化合物Eを次々と縮合重合させると、高分子化合物Fが得られ、これは繊維として衣料品に用いられる他、樹脂としてペットボトルの原料となる。
一方、化合物Cに濃硫酸を加え170°Cで加熱したところ、化合物Cおよびその構造異性体H、Iが生成した。化合物Hと化合物Iはシスートランス異性体の関係にあり、化合物 Hはシス形、化合物Iはトランス形である。化合物Cをオゾン分解したところ、化合物Jと化合物Kが得られた。また、化合物 Hをオゾン分解したところ、ベンズアルデヒドと化合物Lが得られた。化合物Jと化合物Lはフェーリング液を還元し赤色沈澱を生成した。化合物Kはフェーリング液を還元しなかったが、ヨードホルム反応は陽性だった。なお、オゾン分解の反応経路を図1に示す。
問2 化合物D、E、Kの化合物名を解答用紙に書きなさい。
問3 化合物A、I、J、Lの構造式を、3ページにある例にならって解答用紙に書きなさい。
2つの解法レピュニット数の和

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
和を求めよ.
$1+11+111+・・・・\underbrace{111・・・・1}_{n桁}$
この動画を見る
和を求めよ.
$1+11+111+・・・・\underbrace{111・・・・1}_{n桁}$
【数A】場合の数:コンビネーションを使った式の証明
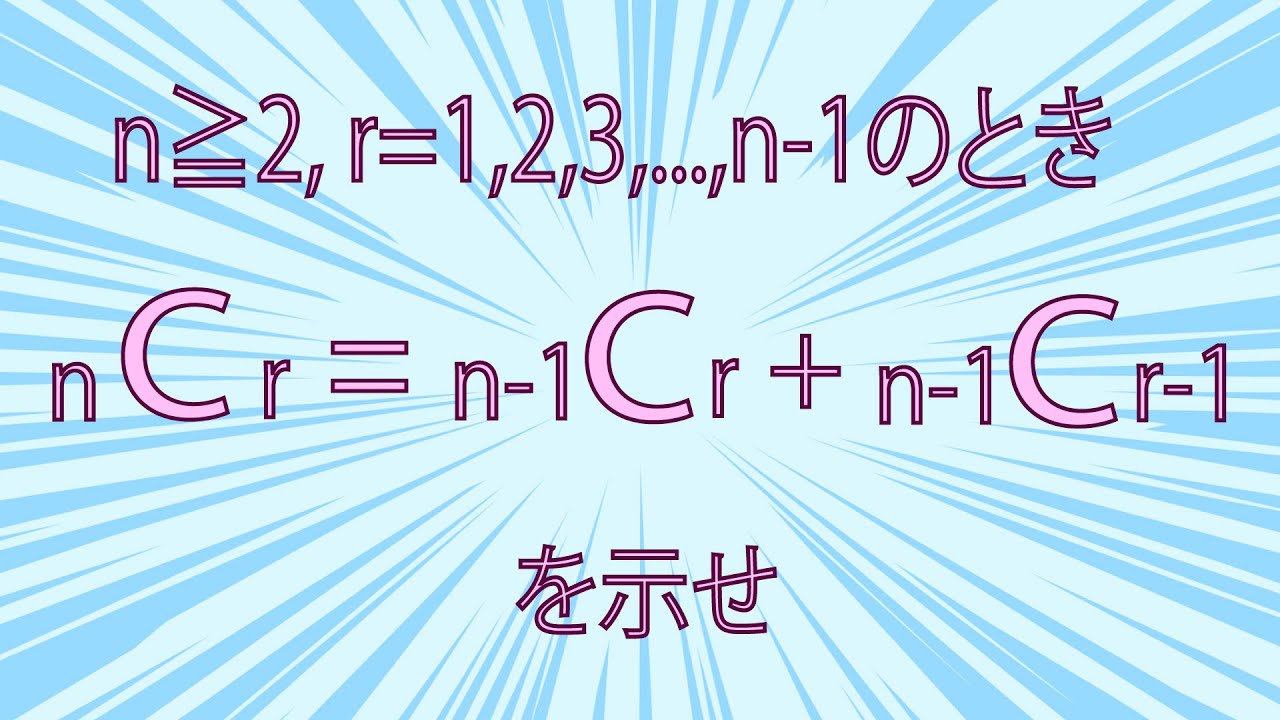
数学「大学入試良問集」【10−2 中点の軌跡】を宇宙一わかりやすく

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$k$を実数とする次の2つの方程式に関し、以下の各問いに各問いに答えよ。
$y=x^2-2x-2$ ・・・①
$y=kx-(k^2+2)$ ・・・②
(1)
式①と式②の表すグラフが2点で交わるための、$k$の値の範囲を求めよ。
(2)
2つの交点を$A,B$とすると、線分$AB$の中点$C$の座標を$k$を用いて表せ。
(3)
$k$の値を変化させるとき、点$C$の軌跡を表す方程式を求め、その式の成り立つ$x$の範囲を求めよ。
この動画を見る
$k$を実数とする次の2つの方程式に関し、以下の各問いに各問いに答えよ。
$y=x^2-2x-2$ ・・・①
$y=kx-(k^2+2)$ ・・・②
(1)
式①と式②の表すグラフが2点で交わるための、$k$の値の範囲を求めよ。
(2)
2つの交点を$A,B$とすると、線分$AB$の中点$C$の座標を$k$を用いて表せ。
(3)
$k$の値を変化させるとき、点$C$の軌跡を表す方程式を求め、その式の成り立つ$x$の範囲を求めよ。
福田のわかった数学〜高校1年生第6回〜絶対値(第2回)

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 絶対値(第2回)
次の方程式、不等式を解け。
(1)$|x+2|=-2x$ (2)$|x+2| \lt -2x$
この動画を見る
数学$\textrm{I}$ 絶対値(第2回)
次の方程式、不等式を解け。
(1)$|x+2|=-2x$ (2)$|x+2| \lt -2x$
#8数検1級1次過去問 重積分積分順序の変更

単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}$
以下を解け.
$\displaystyle \int_{0}^{3} dy \displaystyle \int_{0}^{\sqrt{\frac{y}{3}}}\ \log(x^3-3x+3)dx$
この動画を見る
$\boxed{7}$
以下を解け.
$\displaystyle \int_{0}^{3} dy \displaystyle \int_{0}^{\sqrt{\frac{y}{3}}}\ \log(x^3-3x+3)dx$
どっちがでかい?
数学「大学入試良問集」【10−1 外接する円と軌跡】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#津田塾大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
座標平面上で点$(0,2)$を中心とする半径$1$の円を$C$とする。
$C$に外接し、$x$軸に接する円の中心$P(a,b)$が描く図形の方程式を求めよ。
この動画を見る
座標平面上で点$(0,2)$を中心とする半径$1$の円を$C$とする。
$C$に外接し、$x$軸に接する円の中心$P(a,b)$が描く図形の方程式を求めよ。
