 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$自然数とする.これを解け.
$n^2+785=3^m$
この動画を見る
$m,n$自然数とする.これを解け.
$n^2+785=3^m$
大分大 指数 最小値

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#大分大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$9^x+\displaystyle \frac{1}{9^x}-4a(3^x+\displaystyle \frac{1}{3^x})$の最小値とその時の$x$の値を求めよ
出典:2018年大分大学 過去問
この動画を見る
$9^x+\displaystyle \frac{1}{9^x}-4a(3^x+\displaystyle \frac{1}{3^x})$の最小値とその時の$x$の値を求めよ
出典:2018年大分大学 過去問
1の位が5の数の2乗は1秒で計算できるよ

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$25^2=??$
$35^2=??$
$45^2=??$
$55^2=??$
$65^2=??$
$75^2=??$
$85^2=??$
$95^2=??$
$105^2=??$
$115^2=??$
・
・
・
$195^2=??$
$205^2=??$
この動画を見る
$25^2=??$
$35^2=??$
$45^2=??$
$55^2=??$
$65^2=??$
$75^2=??$
$85^2=??$
$95^2=??$
$105^2=??$
$115^2=??$
・
・
・
$195^2=??$
$205^2=??$
2020整式の剰余

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(x+1)^{2020}$を$x^2+1$で割った余りを求めよ
この動画を見る
$(x+1)^{2020}$を$x^2+1$で割った余りを求めよ
平面ベクトルと空間ベクトル

室蘭工業大 漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#室蘭工業大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=\displaystyle \frac{1}{2}$ 一般項を求めよ
$a_{n+1}=\displaystyle \frac{(n+1)a_n}{n+3^na_n}$
出典:2018年蘭工業大学 過去問
この動画を見る
$a_1=\displaystyle \frac{1}{2}$ 一般項を求めよ
$a_{n+1}=\displaystyle \frac{(n+1)a_n}{n+3^na_n}$
出典:2018年蘭工業大学 過去問
空間座標の導入!!

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点$P(2,3,4)$に対して
(1)$xy$平面に関して対称な点の座標は( , , )
(2)$yz$平面に関して対称な点の座標は( , , )
(3)$zx$平面に関して対称な点の座標は( , , )
(4)$x$軸平面に関して対称な点の座標は( , , )
(5)$y$軸平面に関して対称な点の座標は( , , )
(6)$z$軸平面に関して対称な点の座標は( , , )
(7)原点平面に関して対称な点の座標は( , , )
この動画を見る
点$P(2,3,4)$に対して
(1)$xy$平面に関して対称な点の座標は( , , )
(2)$yz$平面に関して対称な点の座標は( , , )
(3)$zx$平面に関して対称な点の座標は( , , )
(4)$x$軸平面に関して対称な点の座標は( , , )
(5)$y$軸平面に関して対称な点の座標は( , , )
(6)$z$軸平面に関して対称な点の座標は( , , )
(7)原点平面に関して対称な点の座標は( , , )
確率

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
始めに赤箱から球を個取り出して戻す。
次回以降は取り出した玉と同じ色の箱から玉を取り出す。
$n$回目に赤が出る確率を求めよ
この動画を見る
始めに赤箱から球を個取り出して戻す。
次回以降は取り出した玉と同じ色の箱から玉を取り出す。
$n$回目に赤が出る確率を求めよ
京都大 確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#京都大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1~5$の数を等確率で入れて$n$桁の整数を作る
$X$が3で割り切れる確率を求めよ
出典:2017年京都大学 過去問
この動画を見る
$1~5$の数を等確率で入れて$n$桁の整数を作る
$X$が3で割り切れる確率を求めよ
出典:2017年京都大学 過去問
2直線の交点の位置ベクトル(3通りの説明)

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
数学を数楽に
問題文全文(内容文):
$\overrightarrow{ OA }=\vec{ a },\overrightarrow{ OB }=\vec{ b }$のとき
$\overrightarrow{ OP }$を$\vec{ a },\vec{ b }$で表せ。
この動画を見る
$\overrightarrow{ OA }=\vec{ a },\overrightarrow{ OB }=\vec{ b }$のとき
$\overrightarrow{ OP }$を$\vec{ a },\vec{ b }$で表せ。
内分の位置ベクトル

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
数学を数楽に
問題文全文(内容文):
(1)$\vec{ P }$を$\vec{ a },\vec{ b }$で表せ
(2)$\overrightarrow{ OQ }=\displaystyle \frac{3\vec{ a }+2\vec{ b }}{9}$のとき点$Q$はどこ?
この動画を見る
(1)$\vec{ P }$を$\vec{ a },\vec{ b }$で表せ
(2)$\overrightarrow{ OQ }=\displaystyle \frac{3\vec{ a }+2\vec{ b }}{9}$のとき点$Q$はどこ?
ベストを出すための「あと20日」のメンタル調整術~センター9割の受験勉強法【篠原好】

単元:
#センター試験・共通テスト関連#センター試験#その他#勉強法#その他
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
センター試験まであと20日!
「ベストを出すためのメンタル調整術」についてお話しています。
この動画を見る
センター試験まであと20日!
「ベストを出すためのメンタル調整術」についてお話しています。
2020整数問題

✖️チョイスヘキサゴン!!(バッテンでチョイスして壁差ゴン!!)

内積と三角形の面積

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
数学を数楽に
問題文全文(内容文):
$\triangle \textrm{OAB}$の面積を求めよ。
この動画を見る
$\triangle \textrm{OAB}$の面積を求めよ。
ベクトルの内積とは??

大阪市立大 微分と接線の基本問題

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#大阪市立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^3+2x^2-4x$に$(0,k)$から引ける接線の数を求めよ
出典:大阪市立大学 過去問
この動画を見る
$f(x)=x^3+2x^2-4x$に$(0,k)$から引ける接線の数を求めよ
出典:大阪市立大学 過去問
ベクトルの導入

合同式の基礎 累乗の式変形

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3^{2n+1}+4^{3n-1}$が7の倍数となる自然数$n$を3つ求めよ
この動画を見る
$3^{2n+1}+4^{3n-1}$が7の倍数となる自然数$n$を3つ求めよ
大阪大 虚数解を持つ3次方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p,q$実数 $q \neq 0$
$p+qi$が$x^3+px+10=0$の解である。
$p,q$を求めよ
出典:2000年大阪大学 過去問
この動画を見る
$p,q$実数 $q \neq 0$
$p+qi$が$x^3+px+10=0$の解である。
$p,q$を求めよ
出典:2000年大阪大学 過去問
【数学A】7の倍数の見分け方を伝授します【3桁ずつ分割!map mapで計算せよ!】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学A】7の倍数の見分け方説明動画です
この動画を見る
【数学A】7の倍数の見分け方説明動画です
大島さんの自習室 もっちゃん授業を観たら突然復習し始めた

もっちゃんと学ぶ数学 Σの公式 導出

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \sum_{k=1}^n k=?$
$\displaystyle \sum_{k=1}^n k^2=?$
この動画を見る
$\displaystyle \sum_{k=1}^n k=?$
$\displaystyle \sum_{k=1}^n k^2=?$
大阪大 区分求積法 ヨビノリ病欠 代講ヤス

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#大阪大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_n=\displaystyle \sum_{k=1}^n \displaystyle \frac{[\sqrt{ 2n^2-k^2 }]}{n^2}$
$\displaystyle \lim_{ n \to \infty } a_n$を求めよ
出典:2000年大阪大学 過去問
この動画を見る
$a_n=\displaystyle \sum_{k=1}^n \displaystyle \frac{[\sqrt{ 2n^2-k^2 }]}{n^2}$
$\displaystyle \lim_{ n \to \infty } a_n$を求めよ
出典:2000年大阪大学 過去問
東大法学部大島が語る過去問主義

【高校数学】立体の問題のポイント・重要公式集【コツさえつかめば怖くない!】

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【高校数学】立体の問題のポイント・重要公式集
-----------------
1⃣
球の中に正四面体ABCDが内接している。
正四面体ABCDの一辺の長さをaとし、球の半径をRとするとき、Rをaを用いて示しなさい。
2⃣
正四面体ABCDに球が内接している。
このとき、球の半径rをaを用いて表しなさい。
この動画を見る
【高校数学】立体の問題のポイント・重要公式集
-----------------
1⃣
球の中に正四面体ABCDが内接している。
正四面体ABCDの一辺の長さをaとし、球の半径をRとするとき、Rをaを用いて示しなさい。
2⃣
正四面体ABCDに球が内接している。
このとき、球の半径rをaを用いて表しなさい。
室蘭工業大 整式の剰余

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#室蘭工業大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$m,n$自然数
(1)
$x^{3m}+1$を$x^3-1$で割った余りを求めよ
(2)
$x^n+1$を$x^2+x+1$で割った余りを求めよ
出典:1998年室蘭工業大学 過去問
この動画を見る
$m,n$自然数
(1)
$x^{3m}+1$を$x^3-1$で割った余りを求めよ
(2)
$x^n+1$を$x^2+x+1$で割った余りを求めよ
出典:1998年室蘭工業大学 過去問
整数問題
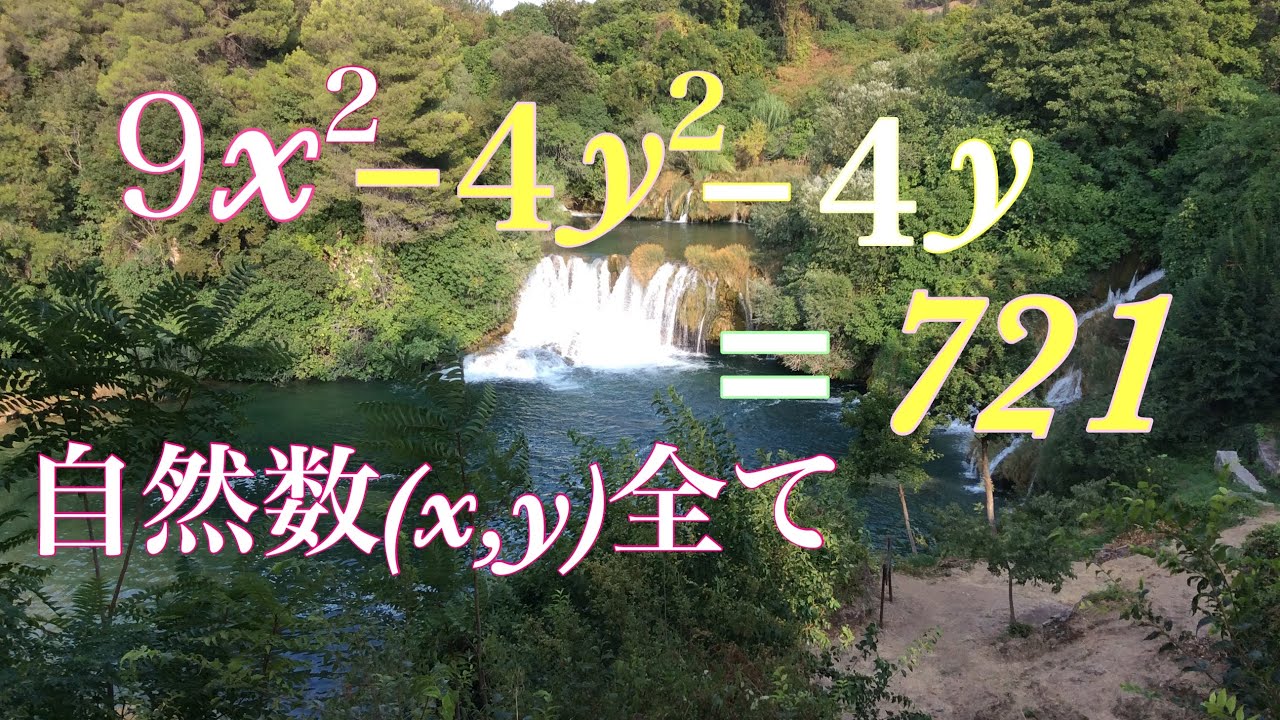
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$9x^2-4y^2-4y=721$
自然数$(x,y)$をすべて求めよ
この動画を見る
$9x^2-4y^2-4y=721$
自然数$(x,y)$をすべて求めよ
日本医科大 複素数

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#日本医科大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\theta=\displaystyle \frac{\pi}{7}$ $z=\cos\theta+i \sin\theta$
(1)
$\cos\theta,\cos2\theta,\cos3\theta$を$z$で表せ
(2)
$\cos\theta・\cos2\theta・\cos3\theta$
(3)
$\cos\theta+\cos3\theta+\cos5\theta$の値を求めよ
出典:日本医科大学 過去問
この動画を見る
$\theta=\displaystyle \frac{\pi}{7}$ $z=\cos\theta+i \sin\theta$
(1)
$\cos\theta,\cos2\theta,\cos3\theta$を$z$で表せ
(2)
$\cos\theta・\cos2\theta・\cos3\theta$
(3)
$\cos\theta+\cos3\theta+\cos5\theta$の値を求めよ
出典:日本医科大学 過去問
COS36°を3通りで求めてね

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\cos36^{ \circ }$を3通りで求めよ
この動画を見る
$\cos36^{ \circ }$を3通りで求めよ
