 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
#産業医科大学2024#区分級積法_41

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{n\to\infty}\displaystyle \sum_{i=1}^{n} \dfrac{i\sqrt{i^2+n^2}}{n^3}$
を解け.
2022産業医科大学過去問題
この動画を見る
$\displaystyle \lim_{n\to\infty}\displaystyle \sum_{i=1}^{n} \dfrac{i\sqrt{i^2+n^2}}{n^3}$
を解け.
2022産業医科大学過去問題
福田のおもしろ数学249〜絶対値の付いた不等式が常に成り立つ条件

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
任意の $x,y$ について $|\sin x - \sin y| \leqq k|x-y|$ が成り立つような定数 $k$ の最小値を求めよ。
この動画を見る
任意の $x,y$ について $|\sin x - \sin y| \leqq k|x-y|$ が成り立つような定数 $k$ の最小値を求めよ。
激ムズ積分 大技で卍固め By BBBさん
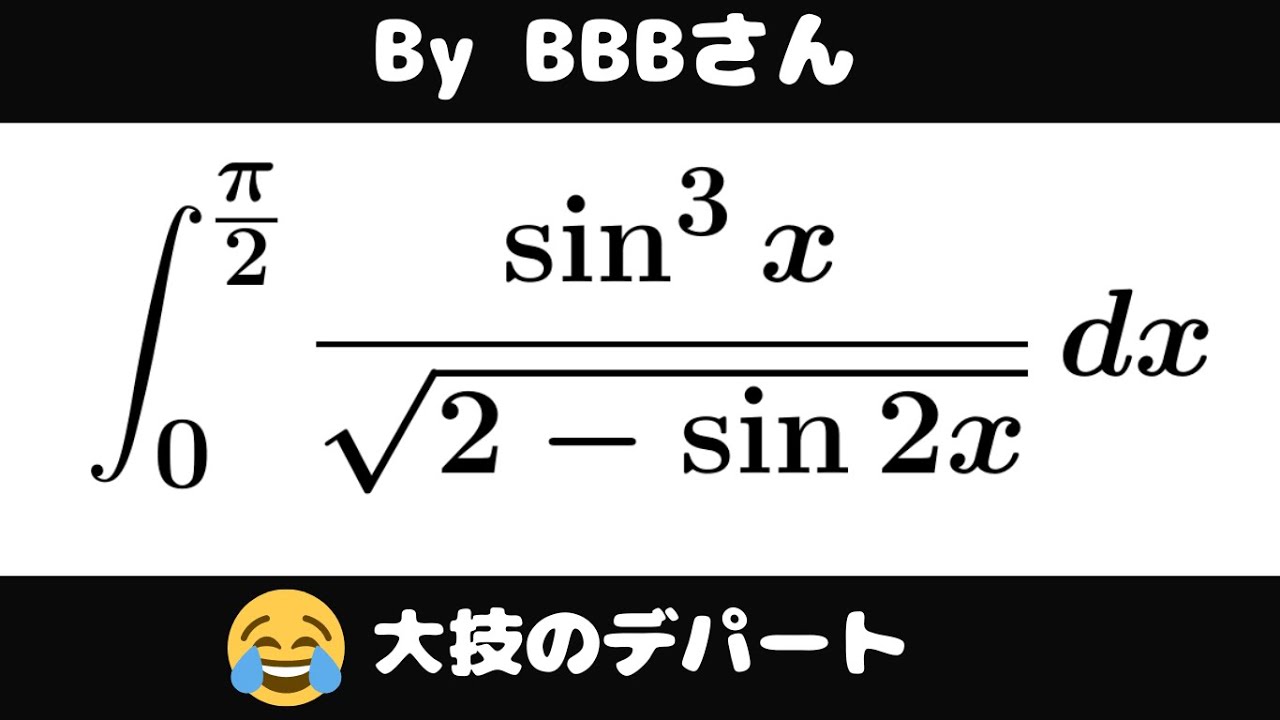
単元:
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \dfrac{\sin^3x}{\sqrt{2-\sin 2x}}dx$
を解け.
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \dfrac{\sin^3x}{\sqrt{2-\sin 2x}}dx$
を解け.
福田の数学〜明治大学2024理工学部第1問(2)〜空間ベクトルと四面体の体積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$k$ を正の実数とし、座標空間内の $4$ 点 $\mathrm{O}(0,0,0),$ $\mathrm{A}(k,2,1),$ $\mathrm{B}(-k,1,2),$ $\mathrm{C}(1,1,1)$ を考える。 $2$ つのベクトル $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ は垂直であるとする。また、 $3$ 点 $\mathrm{O},\mathrm{A},\mathrm{B}$ を通る平面を $\alpha$ とし、点 $\mathrm{C}$ から$\alpha$ へ下ろした垂線と平面 $\alpha$ の交点を $\mathrm{H}$ とする。このとき、 $k=\fbox{キ}$ であり、 $\triangle \mathrm{OAB}$ の面積は $\displaystyle \frac{\fbox{ク}}{\fbox{ケ}}$ である。また、$\overrightarrow{\mathrm{OH}}=$$\displaystyle \frac{\fbox{コ}}{\fbox{サ}} \overrightarrow{\mathrm{OA}}$$\displaystyle + \frac{\fbox{シ}}{\fbox{ス}} \overrightarrow{\mathrm{OB}}$ であり、四面体 $\mathrm{OABC}$ の体積は $\displaystyle \frac{\fbox{セ}}{\fbox{ソ}}$ である。
この動画を見る
$k$ を正の実数とし、座標空間内の $4$ 点 $\mathrm{O}(0,0,0),$ $\mathrm{A}(k,2,1),$ $\mathrm{B}(-k,1,2),$ $\mathrm{C}(1,1,1)$ を考える。 $2$ つのベクトル $\overrightarrow{\mathrm{OA}}$ と $\overrightarrow{\mathrm{OB}}$ は垂直であるとする。また、 $3$ 点 $\mathrm{O},\mathrm{A},\mathrm{B}$ を通る平面を $\alpha$ とし、点 $\mathrm{C}$ から$\alpha$ へ下ろした垂線と平面 $\alpha$ の交点を $\mathrm{H}$ とする。このとき、 $k=\fbox{キ}$ であり、 $\triangle \mathrm{OAB}$ の面積は $\displaystyle \frac{\fbox{ク}}{\fbox{ケ}}$ である。また、$\overrightarrow{\mathrm{OH}}=$$\displaystyle \frac{\fbox{コ}}{\fbox{サ}} \overrightarrow{\mathrm{OA}}$$\displaystyle + \frac{\fbox{シ}}{\fbox{ス}} \overrightarrow{\mathrm{OB}}$ であり、四面体 $\mathrm{OABC}$ の体積は $\displaystyle \frac{\fbox{セ}}{\fbox{ソ}}$ である。
#関西大学2024#不定積分_40
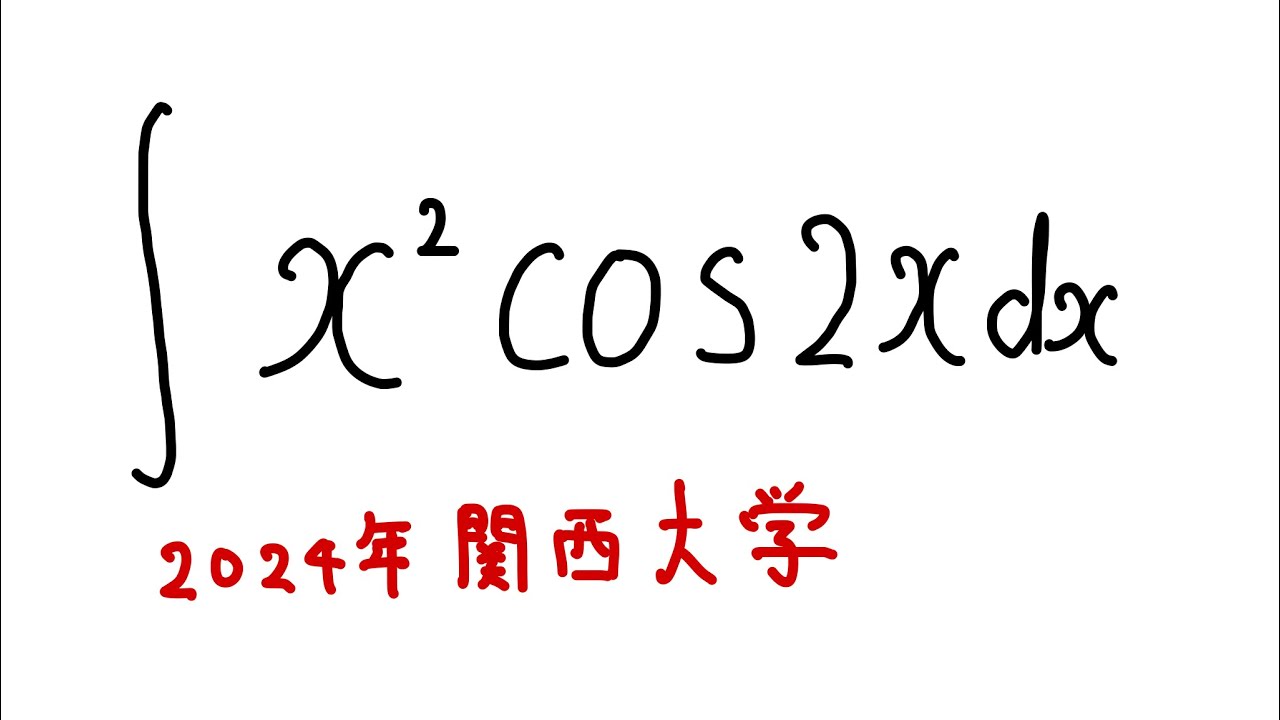
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} x^2\cos \ 2x\ dx$
を解け.
2022関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} x^2\cos \ 2x\ dx$
を解け.
2022関西大学過去問題
#関西大学2022#不定積分_39
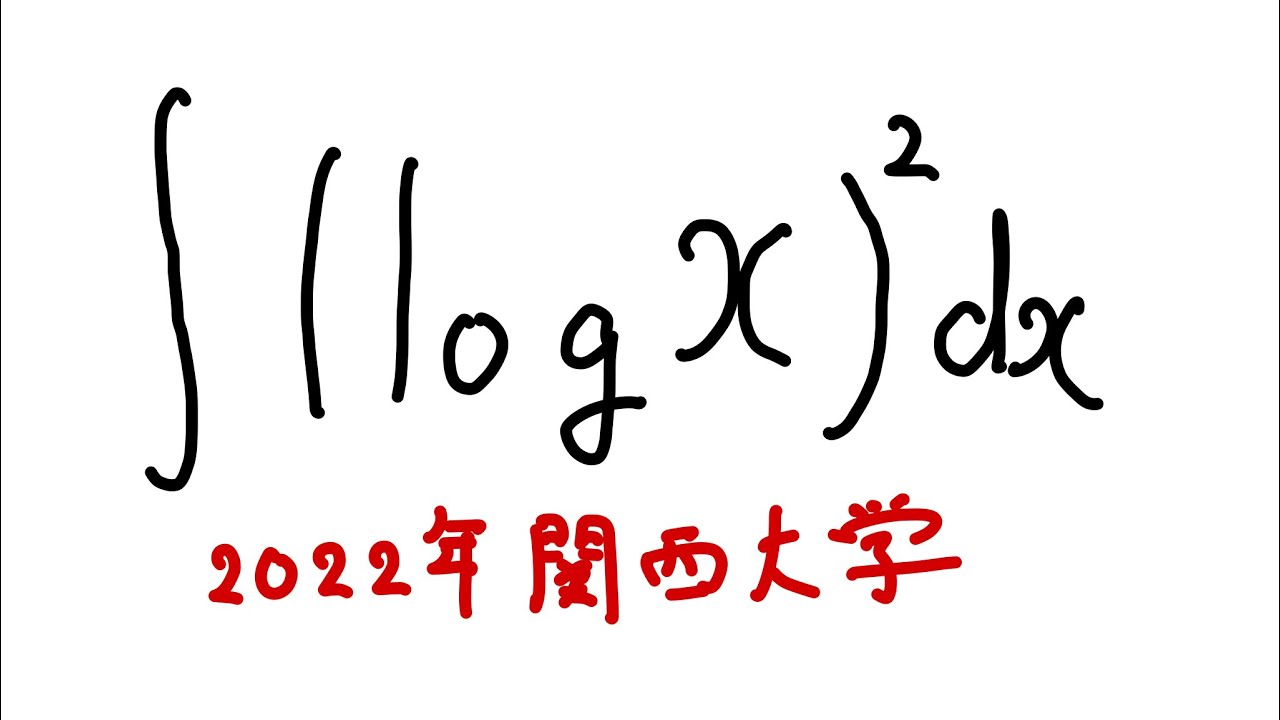
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} (\log x^2 )dx$
を解け.
2022関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} (\log x^2 )dx$
を解け.
2022関西大学過去問題
福田のおもしろ数学248〜cos(cox x)=sin(sin x)の解が存在するかどうかを調べる

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
方程式 $\cos (\cos x) = \sin (\sin x)$ は実数解をもつか?
この動画を見る
方程式 $\cos (\cos x) = \sin (\sin x)$ は実数解をもつか?
〇〇きの定理で解説!!
〇〇きの定理で解説!!

大学入試問題#925「初手が見えれば一直線」 #関西大学2023

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{}^{} \left(\dfrac{1}{\sqrt x}\ \sin\ (3\sqrt x)\ \cos \ (5\sqrt x)\right)dx$
を解け.
2023関西大学過去問題
この動画を見る
$\displaystyle \int_{}^{} \left(\dfrac{1}{\sqrt x}\ \sin\ (3\sqrt x)\ \cos \ (5\sqrt x)\right)dx$
を解け.
2023関西大学過去問題
福田の数学〜明治大学2024理工学部第1問(1)〜高次方程式と整数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$k,l,m$ を定数とする。関数 $f(x)=4x^3+kx^2-lx+m$ は次の $3$ つの条件を満たすとする。
・ $k,l,m$ は $0$ 以上の整数である。
・ $x$ に関する方程式 $f(x)=0$ は $\frac{1}{2}$ を解にもつ。
・ $f(x)$ を微分して得られる整式を $f'(x)$ とするとき、 $f'(x)$ を $x+2$ で割ったときの余りは $41$ である。
このとき、$k=\fbox{ア},$ $l=\fbox{イ},$ $m=\fbox{ウ}$ であり、方程式 $f(x)=0$ の $\frac{1}{2}$ 以外の解は $\displaystyle -\frac{\fbox{エ}}{\fbox{オ}}$ と $\fbox{カ}$ である。
この動画を見る
$k,l,m$ を定数とする。関数 $f(x)=4x^3+kx^2-lx+m$ は次の $3$ つの条件を満たすとする。
・ $k,l,m$ は $0$ 以上の整数である。
・ $x$ に関する方程式 $f(x)=0$ は $\frac{1}{2}$ を解にもつ。
・ $f(x)$ を微分して得られる整式を $f'(x)$ とするとき、 $f'(x)$ を $x+2$ で割ったときの余りは $41$ である。
このとき、$k=\fbox{ア},$ $l=\fbox{イ},$ $m=\fbox{ウ}$ であり、方程式 $f(x)=0$ の $\frac{1}{2}$ 以外の解は $\displaystyle -\frac{\fbox{エ}}{\fbox{オ}}$ と $\fbox{カ}$ である。
#関西大学2022#定積分_38
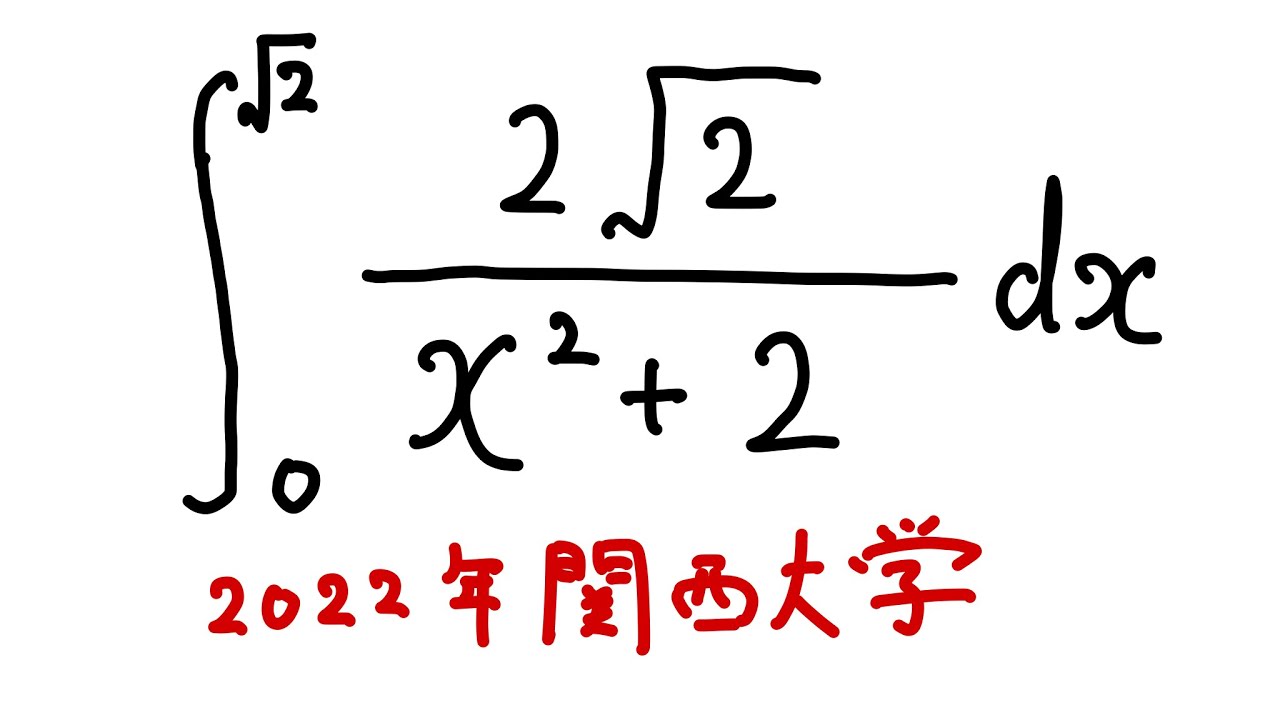
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt2} \dfrac{2\sqrt2}{x^2+2}dx$
を解け.
2022関西大学過去問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt2} \dfrac{2\sqrt2}{x^2+2}dx$
を解け.
2022関西大学過去問題
福田のおもしろ数学247〜複雑な無理方程式の解を1つ見つける

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$
5(\sqrt{1-x}+\sqrt{1+x})=6x+8\sqrt{1-x^2}
$の解を1つ求めて下さい。
この動画を見る
$
5(\sqrt{1-x}+\sqrt{1+x})=6x+8\sqrt{1-x^2}
$の解を1つ求めて下さい。
福田のおもしろ数学246〜分数式の極限と区分求積

単元:
#関数と極限#積分とその応用#関数の極限#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \frac{(1+2+…+n)^5}{(1^4+2^4+…+n^4)^2}$
を求めて下さい。
この動画を見る
$\displaystyle \lim_{ n \to \infty } \frac{(1+2+…+n)^5}{(1^4+2^4+…+n^4)^2}$
を求めて下さい。
定点の座標を求めよ 高校数学
定点の座標を求めよ 高校数学

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
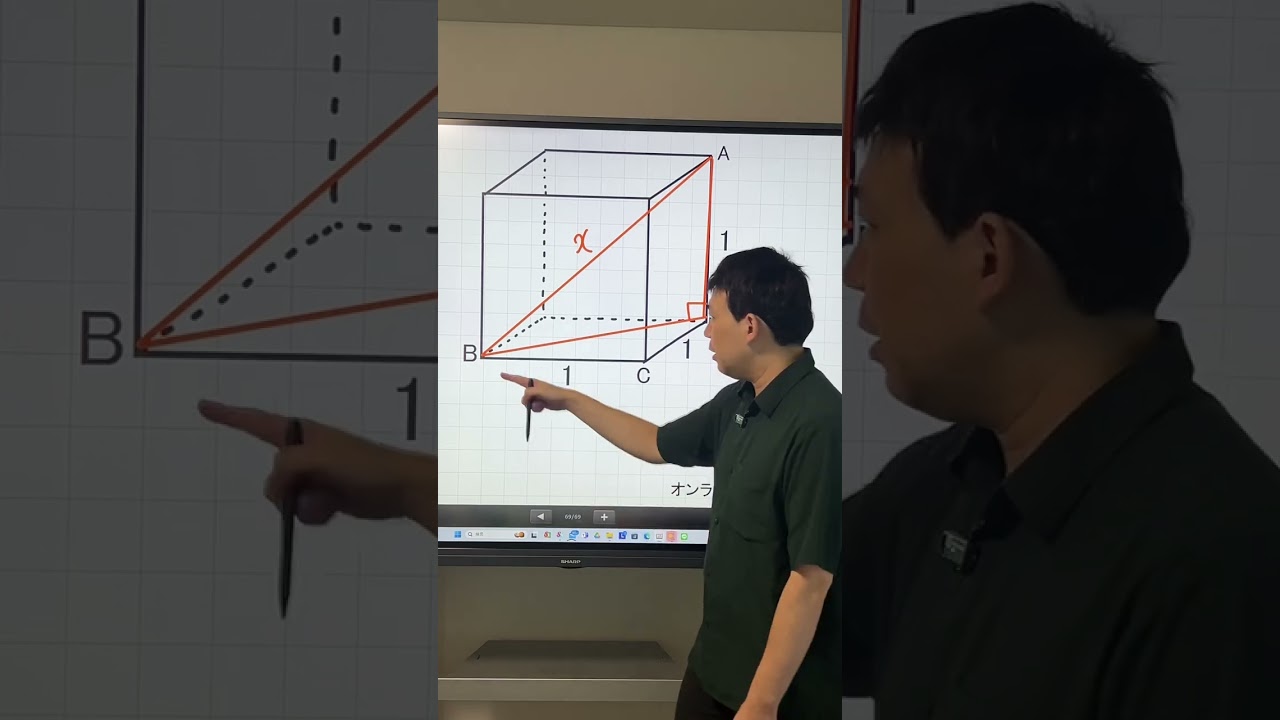
定数kがどんな値を取っても
直線$kx-y+5k=0$が通る
定点の座標を求めよ
この動画を見る
定数kがどんな値を取っても
直線$kx-y+5k=0$が通る
定点の座標を求めよ
難易度バリ高の極限 by 餃子n人前さん ※作成者の解答を参考に動画を作成しています。

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,$ $a_{n+1}+a_n=\displaystyle \frac{1}{n}$のとき、
$\displaystyle \lim_{ n \to \infty } |na_n|$を求めよ
この動画を見る
$a_1=1,$ $a_{n+1}+a_n=\displaystyle \frac{1}{n}$のとき、
$\displaystyle \lim_{ n \to \infty } |na_n|$を求めよ
福田の数学〜明治大学2024全学部統一III第3問〜外サイクロイド曲線と曲線の長さ

単元:
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3} a\gt 0$とする。座標平面で、原点$O$を中心とする半径$a$の定円を$C_1$とし、$C_1$と外接する半径$a$の円を$C_2$とする。円$C_2$が定円$C_1$と外接しながらすべることなく転がるとき、$C_2$上の定点$P$が描く曲線を考えたい。始めに$C_2$の中心が$(2a,0)$にあり、$P$が$(a,0)$にあるとする。$C_2$の中心が点$(2a,0)$から原点$O$を中心に反時計回りに$θ$だけ回転した位置にきたとき、$C_1$と$C_2$の接点を通る$C_1$と$C_2$の共通の接線を$l_θ$とする。$l_θ$の方程式は$a=(\boxed{ア})x+(\boxed{イ})y$である。このとき、$P$は直線$l_θ$に関して$(a,0)$と対称な点であるので、$P$の座標を$(x,y)$とすると、$P$の軌跡は$θ$を媒介変数として$x=2a(\boxed{ウ})cosθ+a, y=2a(\boxed{ウ})sinθ$と表される。
$x$と$y$をそれぞれ$θ$で微分すると$\frac{dx}{dθ}=2a(\boxed{エ}),\frac{dy}{dθ}=2a(\boxed{オ})$となるので、$θ$が0から2まで動くとき、$P$が描く曲線の長さは$\boxed{カキ}a$である。
この動画を見る
$\boxed{3} a\gt 0$とする。座標平面で、原点$O$を中心とする半径$a$の定円を$C_1$とし、$C_1$と外接する半径$a$の円を$C_2$とする。円$C_2$が定円$C_1$と外接しながらすべることなく転がるとき、$C_2$上の定点$P$が描く曲線を考えたい。始めに$C_2$の中心が$(2a,0)$にあり、$P$が$(a,0)$にあるとする。$C_2$の中心が点$(2a,0)$から原点$O$を中心に反時計回りに$θ$だけ回転した位置にきたとき、$C_1$と$C_2$の接点を通る$C_1$と$C_2$の共通の接線を$l_θ$とする。$l_θ$の方程式は$a=(\boxed{ア})x+(\boxed{イ})y$である。このとき、$P$は直線$l_θ$に関して$(a,0)$と対称な点であるので、$P$の座標を$(x,y)$とすると、$P$の軌跡は$θ$を媒介変数として$x=2a(\boxed{ウ})cosθ+a, y=2a(\boxed{ウ})sinθ$と表される。
$x$と$y$をそれぞれ$θ$で微分すると$\frac{dx}{dθ}=2a(\boxed{エ}),\frac{dy}{dθ}=2a(\boxed{オ})$となるので、$θ$が0から2まで動くとき、$P$が描く曲線の長さは$\boxed{カキ}a$である。
#岩手大学2024#定積分_34
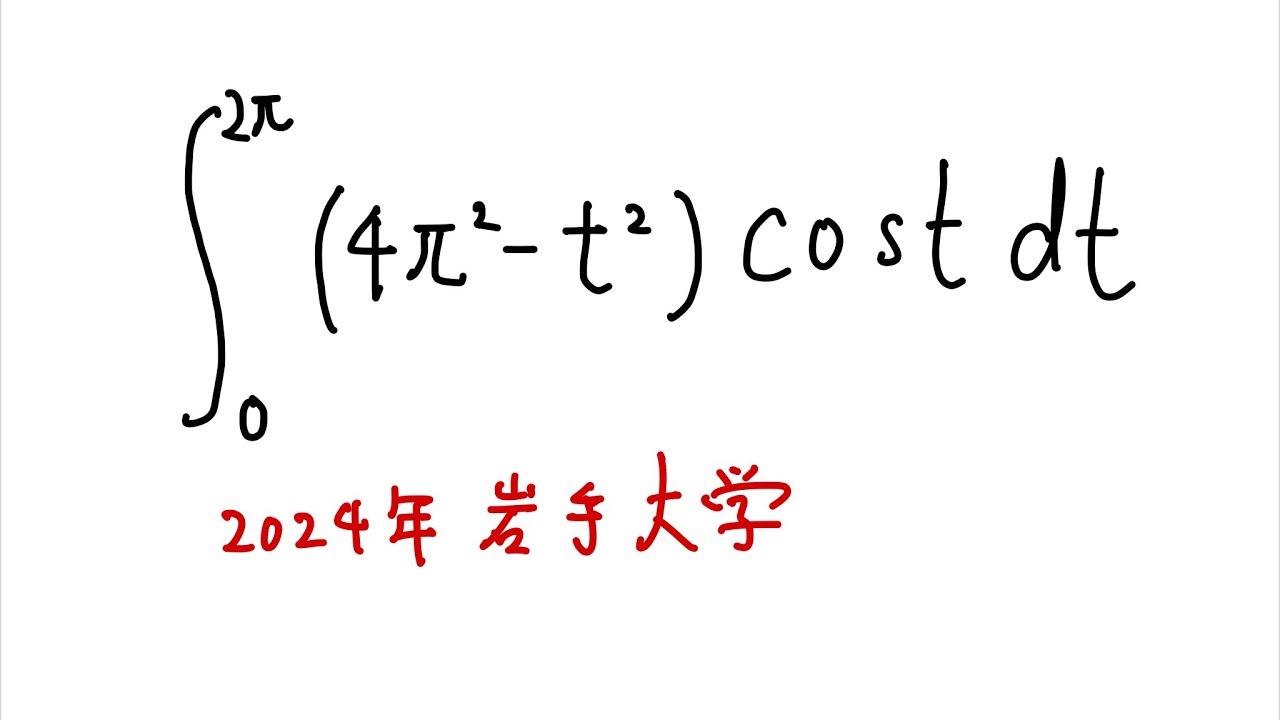
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi} (4\pi^2-t^2)\cos t dt$
出典:2024年岩手大学
この動画を見る
$\displaystyle \int_{0}^{2\pi} (4\pi^2-t^2)\cos t dt$
出典:2024年岩手大学
【数学】絶対に「時間配分」でミスらなくなる方法

単元:
#その他#勉強法#その他#数学(高校生)#その他
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
【数学】絶対に「時間配分」でミスらなくなる方法を解説していきます。
この動画を見る
【数学】絶対に「時間配分」でミスらなくなる方法を解説していきます。
#福島大学2023#定積分_33

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\sqrt{ 3 }}^{ 1 } \sqrt{ 4-x^2 } dx$
出典:2023年福島大学
この動画を見る
$\displaystyle \int_{-\sqrt{ 3 }}^{ 1 } \sqrt{ 4-x^2 } dx$
出典:2023年福島大学
福田のおもしろ数学245〜3乗根を含む2重根号の計算

福田の数学〜明治大学2024全学部統一III第2問〜複素数平面上の点の移動と確率

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$i$は虚数単位とし、$\omega =\frac{-1+\sqrt{3}i}{2}$とする。
投げたときに表と裏の出る確率がそれぞれ$\frac{1}{2}$の硬貨を用意する$ z_{0} = 0$ とおき、この硬貨を4回投げて、複素数$z_1, z_2, z_3, z_4$を次の規則により定める。
$n = 1, 2, 3, 4$ に対して、$n$回目に投げたとき、表が出たならば$z_n = \omega z_{n-1}$とし、 裏が出れば$ z_n = z_{n−1}+1$とする。例えば、4回投げた結果、順に「裏、表、裏、 表」と出た場合、$z_{1} = z_{0} + 1 = 1, z_2 = \omega z_1 = \omega, z_{3} = z_{2} + 1 = \omega + 1, z_{4} = \omega z_{3} = \omega ^ 2 + \omega$ となる。
上の規則により$z_1, z_2, z_3, z_4$を定めたとき、$P$を$ z_{4} = 0 $となる確率、$Q$を$ z_{4} = 1$ となる確率、$R$を $z_{4} = \omega + 1$ となる確率とすると$2^4P=\fbox{ア}、2Q=\fbox{イ}, 2R=\fbox{ウ}$である。また、$S$を$|z_4|=1$となる確率、$T$を$|z_4|=2$となる確率とすると$2^4S=\fbox{エ}, 2^4T=\fbox{オ}$である。
この動画を見る
$i$は虚数単位とし、$\omega =\frac{-1+\sqrt{3}i}{2}$とする。
投げたときに表と裏の出る確率がそれぞれ$\frac{1}{2}$の硬貨を用意する$ z_{0} = 0$ とおき、この硬貨を4回投げて、複素数$z_1, z_2, z_3, z_4$を次の規則により定める。
$n = 1, 2, 3, 4$ に対して、$n$回目に投げたとき、表が出たならば$z_n = \omega z_{n-1}$とし、 裏が出れば$ z_n = z_{n−1}+1$とする。例えば、4回投げた結果、順に「裏、表、裏、 表」と出た場合、$z_{1} = z_{0} + 1 = 1, z_2 = \omega z_1 = \omega, z_{3} = z_{2} + 1 = \omega + 1, z_{4} = \omega z_{3} = \omega ^ 2 + \omega$ となる。
上の規則により$z_1, z_2, z_3, z_4$を定めたとき、$P$を$ z_{4} = 0 $となる確率、$Q$を$ z_{4} = 1$ となる確率、$R$を $z_{4} = \omega + 1$ となる確率とすると$2^4P=\fbox{ア}、2Q=\fbox{イ}, 2R=\fbox{ウ}$である。また、$S$を$|z_4|=1$となる確率、$T$を$|z_4|=2$となる確率とすると$2^4S=\fbox{エ}, 2^4T=\fbox{オ}$である。
大学入試問題#923「帰納法で解いても良いのかな」

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,$ $a_n \neq 0$
$a_n=3(\sqrt{ S_n }-\sqrt{ S_{n-1} }),2 \leq n$
1.$a_2$を求めよ。
2.$\sqrt{ S_n }$を求めよ。
3.$a_n$を求めよ。
出典:1999年 千葉大学
この動画を見る
$a_1=1,$ $a_n \neq 0$
$a_n=3(\sqrt{ S_n }-\sqrt{ S_{n-1} }),2 \leq n$
1.$a_2$を求めよ。
2.$\sqrt{ S_n }$を求めよ。
3.$a_n$を求めよ。
出典:1999年 千葉大学
#南山大学2021#定積分_32
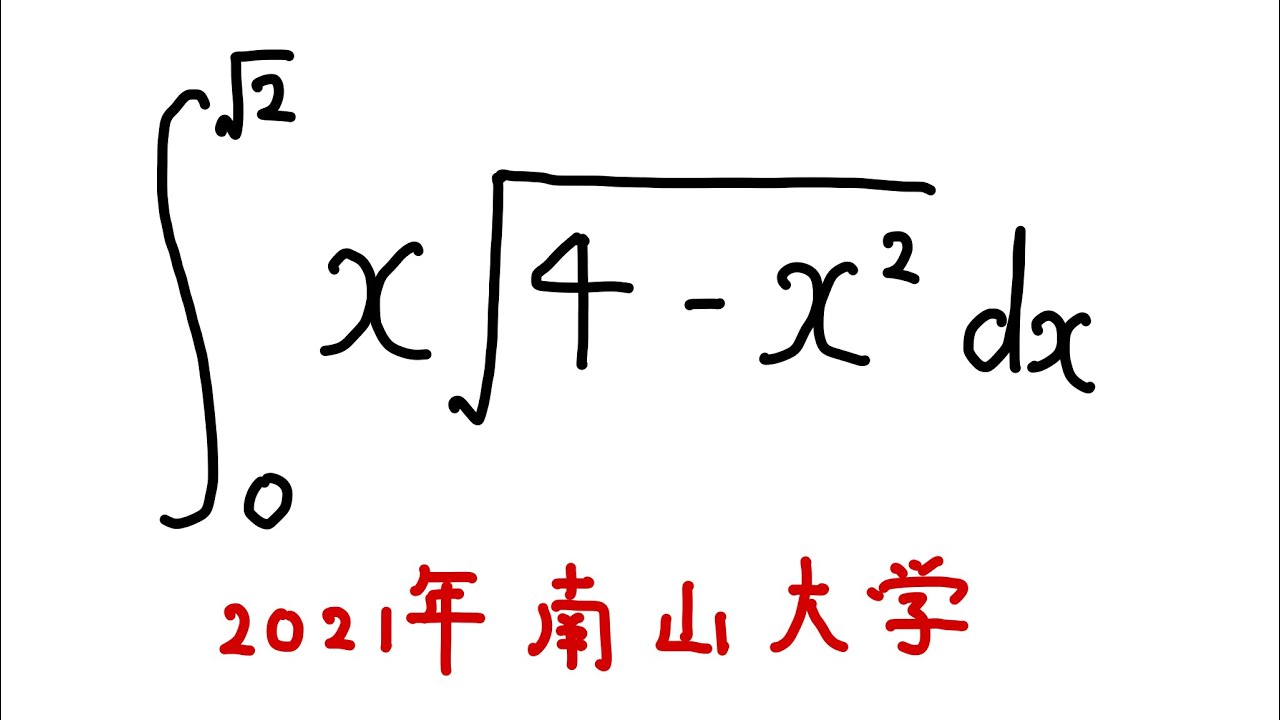
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#南山大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt{ 2 }} x\sqrt{ 4-x^2 } dx$
出典:2021年南山大学
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ 2 }} x\sqrt{ 4-x^2 } dx$
出典:2021年南山大学
#福島大学2024#定積分_31#元高校教員
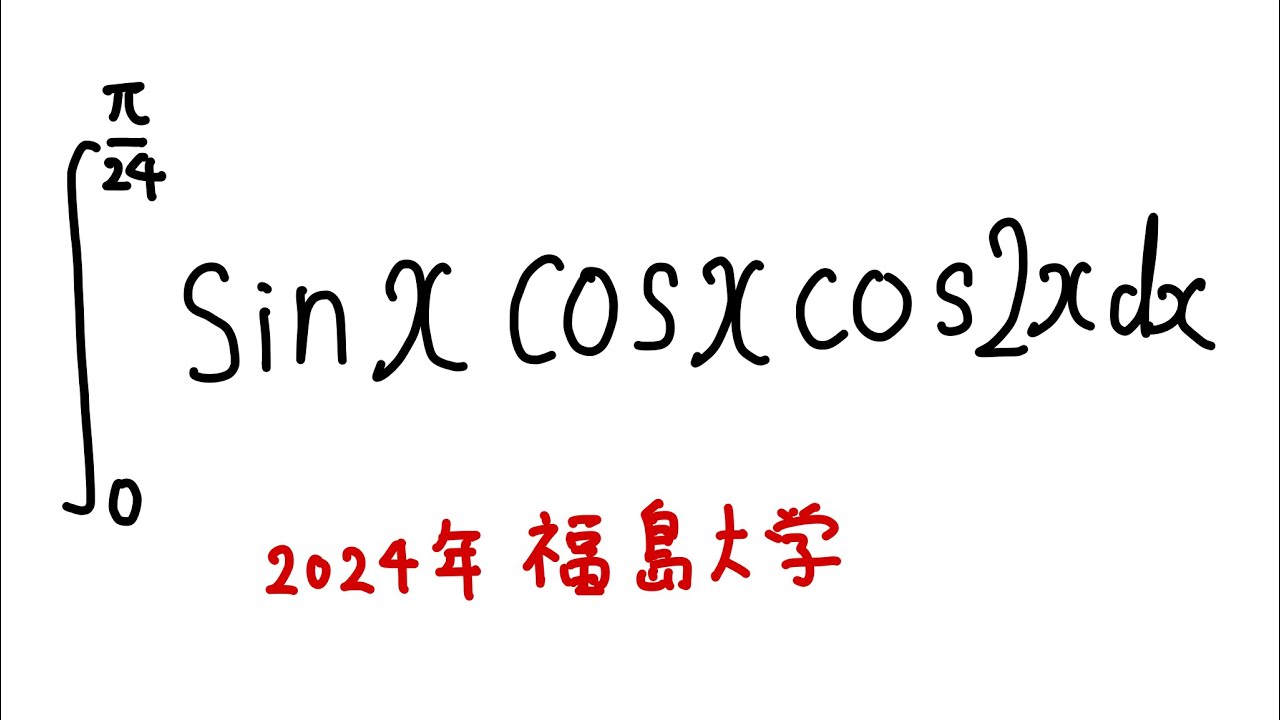
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{24}} \sin x\cos x\cos 2x dx$
出典:2024年福島大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{24}} \sin x\cos x\cos 2x dx$
出典:2024年福島大学
福田のおもしろ数学244〜1次不等式が常に成り立つ条件

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$0\lt m\lt3$であるすべての$m$に対して$2x-1\lt m(x-2)$が成り立つような$x$の範囲を求めよ。
この動画を見る
$0\lt m\lt3$であるすべての$m$に対して$2x-1\lt m(x-2)$が成り立つような$x$の範囲を求めよ。
福田の数学〜明治大学2024全学部統一III第1問(2)〜定積分の計算

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int_{-3}^3 \sqrt{x^2} dx=\fbox{イ}$
この動画を見る
$\displaystyle \int_{-3}^3 \sqrt{x^2} dx=\fbox{イ}$
3点が一直線上 明星
大学入試問題#922「できればスッと解きたい」

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{3}^{4} \displaystyle \frac{4x^2-9x+6}{(x-1)(x-2)^2} dx$
出典:2023年福島大学
この動画を見る
$\displaystyle \int_{3}^{4} \displaystyle \frac{4x^2-9x+6}{(x-1)(x-2)^2} dx$
出典:2023年福島大学
