 高校入試過去問(数学)
高校入試過去問(数学)
 高校入試過去問(数学)
高校入試過去問(数学)
2023高校入試解説18問目 約数の個数が3個 西武文理

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
自然数nの約数は3個その和は57
n=?
2023西部学園文理高等学校
この動画を見る
自然数nの約数は3個その和は57
n=?
2023西部学園文理高等学校
数学の概要を一気につかむ音楽~全国入試問題解法 #shorts #数学 #高校入試 #sound

単元:
#数学(中学生)#中2数学#中3数学#2次方程式#三角形と四角形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ t^2-(4t-1)x+4t^2-2t=0$の2解を$ \alpha,\beta$とすぅる.
3辺の長さが,$5,\alpha,\beta$である三角形が直角三角形である.
$t$の値を求めよ.
慶応志木高校過去問
この動画を見る
$ t^2-(4t-1)x+4t^2-2t=0$の2解を$ \alpha,\beta$とすぅる.
3辺の長さが,$5,\alpha,\beta$である三角形が直角三角形である.
$t$の値を求めよ.
慶応志木高校過去問
2023高校入試解説17問目 3つの内接円 渋谷教育学園幕張
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
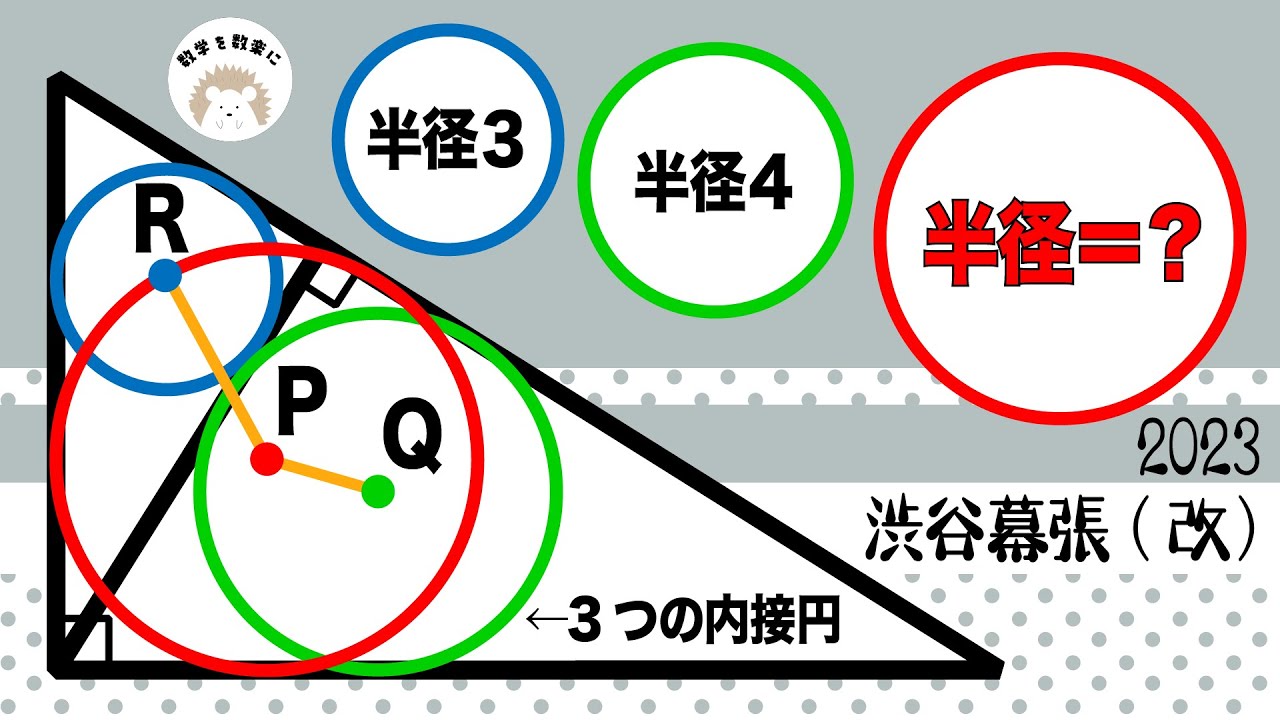
青○:半径3
緑○:半径4
赤○:半径=?
*図は動画内参照
2023渋谷教育学園幕張高等学校(改)
この動画を見る
青○:半径3
緑○:半径4
赤○:半径=?
*図は動画内参照
2023渋谷教育学園幕張高等学校(改)
【暗記するだけじゃなく、考えるだけじゃなく!】整数:和洋国府台女子高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#正の数・負の数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
自然数$n$のすべての約数の和を$f(n)$で表すことにする.
自然数$x$は約数が3個で,$f(x)=57$を満たしている.
$x$を求めよ.
和洋国府台女子高校過去問
この動画を見る
自然数$n$のすべての約数の和を$f(n)$で表すことにする.
自然数$x$は約数が3個で,$f(x)=57$を満たしている.
$x$を求めよ.
和洋国府台女子高校過去問
2023高校入試解説15問目 3種類の4ケタの数 渋谷教育学園幕張 コメントに別解多数あり!!

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
1000~9999の4ケタの整数について2023のようにちょうど3種類の数字が用いられている整数は何個?
2023渋谷教育学園幕張高等学校
この動画を見る
1000~9999の4ケタの整数について2023のようにちょうど3種類の数字が用いられている整数は何個?
2023渋谷教育学園幕張高等学校
2023高校入試解説16問目 3つの内接円 渋谷教育学園幕張

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle QPR=?$
*図は動画内参照
2023渋谷教育学園幕張高等学校
この動画を見る
$\angle QPR=?$
*図は動画内参照
2023渋谷教育学園幕張高等学校
2023高校入試解説14問目 2次方程式 渋谷教育学園幕張

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$(x+\sqrt 3 +\sqrt 5)^2 - 3 \sqrt 5(x-2 \sqrt 5 + \sqrt 3 ) -35 = 0$
2023渋谷教育学園幕張高等学校
この動画を見る
方程式を解け
$(x+\sqrt 3 +\sqrt 5)^2 - 3 \sqrt 5(x-2 \sqrt 5 + \sqrt 3 ) -35 = 0$
2023渋谷教育学園幕張高等学校
2023高校入試解説13問目 因数分解昭和学院秀英

単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$a^2 - 4b^2 +3ab -2bc +2ca$
2023昭和学院秀英高等学校
この動画を見る
因数分解せよ
$a^2 - 4b^2 +3ab -2bc +2ca$
2023昭和学院秀英高等学校
2023高校入試解説12問目 台形と半円 解き方2通り 日大習志野(改)

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$AD=\frac{9}{4}$
半円Oの面積=?
*図は動画内参照
2023日本大学習志野高等学校
この動画を見る
$AD=\frac{9}{4}$
半円Oの面積=?
*図は動画内参照
2023日本大学習志野高等学校
【「分かった」ことを「説明」するには…!】図形:富山県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#空間図形#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
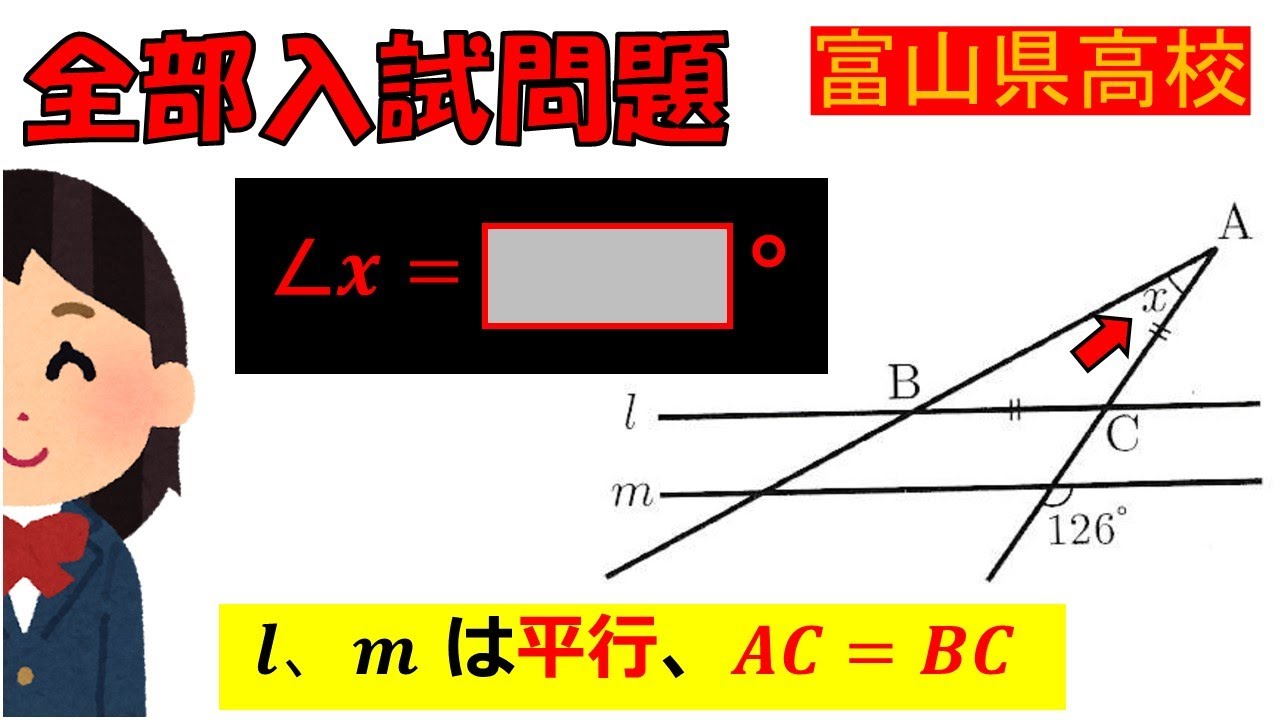
$ l,m$は平行であり,$AC=BC$である.
$ \angle x$は何度であるか.
富山県公立高等学校過去問
この動画を見る
$ l,m$は平行であり,$AC=BC$である.
$ \angle x$は何度であるか.
富山県公立高等学校過去問
2023高校入試解説11問目 円の方程式??2日大習志野(改)
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
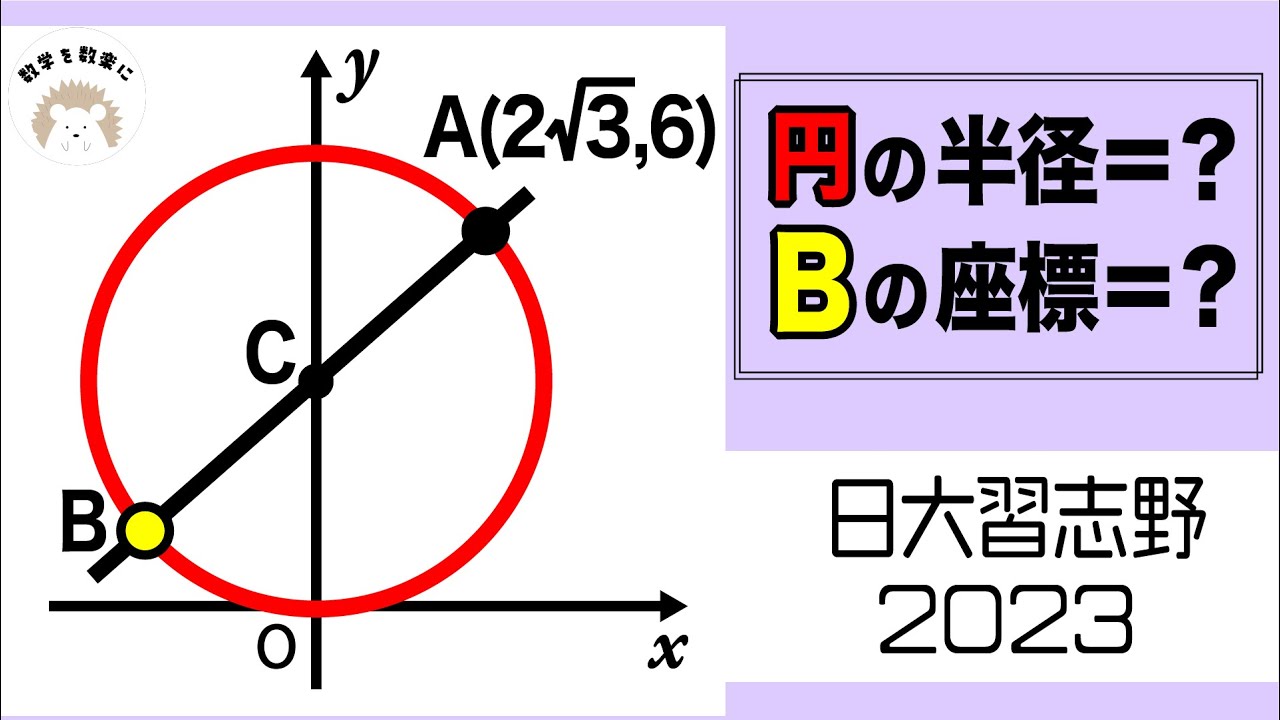
円の半径=?
Bの座標=?
*図は動画内参照
2023日本大学習志野高等学校(改)
この動画を見る
円の半径=?
Bの座標=?
*図は動画内参照
2023日本大学習志野高等学校(改)
2023高校入試解説10問目 二次方程式2023 日大習志野

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$x^2 - 6 \times 17x - 2023 = 0$
2023日本大学習志野高等学校
この動画を見る
2次方程式を解け
$x^2 - 6 \times 17x - 2023 = 0$
2023日本大学習志野高等学校
2023高校入試解説9問目 和と差の積は二乗の差 日大習志野

単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(1+\sqrt 2)(1+\sqrt 8)(1-\frac{1}{\sqrt 2})(1-\frac{1}{\sqrt 8})$
2023日本大学習志野高等学校
この動画を見る
$(1+\sqrt 2)(1+\sqrt 8)(1-\frac{1}{\sqrt 2})(1-\frac{1}{\sqrt 8})$
2023日本大学習志野高等学校
【中学数学】高校入試:2022年度神奈川県立高校入試数学大問5アイ
単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
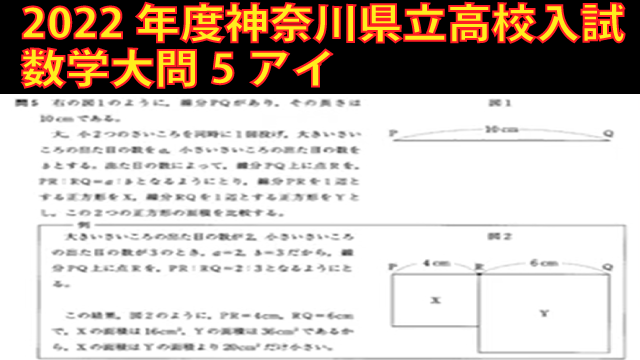
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(ア) Xの面積とYの面積が等しくなる確率は□である。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
この動画を見る
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(ア) Xの面積とYの面積が等しくなる確率は□である。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
【スバラ式 解法!】因数分解:青雲高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (2x+1)^2-3(x-1)(x+2)-27$を因数分解せよ.
青雲高校過去問
この動画を見る
$ (2x+1)^2-3(x-1)(x+2)-27$を因数分解せよ.
青雲高校過去問
【中学数学】円の中にある角度を求めよ~2022年神奈川公立高校入試~【高校受験】

単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
動画内の図において、5点$A,B,C,D,E$は円0の周上の点で、$BE//CD$であり、線分$AD$は$\angle BDE$の二等分線である。
また、点$F$は線分$AD$と線分$CE$との交点である。
このとき、$\angle AFE$を求めよ。
この動画を見る
動画内の図において、5点$A,B,C,D,E$は円0の周上の点で、$BE//CD$であり、線分$AD$は$\angle BDE$の二等分線である。
また、点$F$は線分$AD$と線分$CE$との交点である。
このとき、$\angle AFE$を求めよ。
気分を高めて数学の入試問題を解答するキラキラ~全国入試問題解法 #Shorts #Sound #数学 #高校入試

単元:
#数学(中学生)#中1数学#正の数・負の数#方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2つの自然数$m,n$は
$ 2^m-1=(2n+1)(2n+3)$を満たす.
$ m=6$のとき,$n$の値を求めよ.
慶應義塾高校過去問
この動画を見る
2つの自然数$m,n$は
$ 2^m-1=(2n+1)(2n+3)$を満たす.
$ m=6$のとき,$n$の値を求めよ.
慶應義塾高校過去問
三角形の辺と式の値の正負を調べる 大阪教育大附属平野

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,cが三角形の3辺の長さを表すとき$a^2-b^2-c^2+2bc$の正負を調べよ
大阪教育大学附属高等学校平野校舎(改)
この動画を見る
a,b,cが三角形の3辺の長さを表すとき$a^2-b^2-c^2+2bc$の正負を調べよ
大阪教育大学附属高等学校平野校舎(改)
【方針が決まれば進むだけ!】整数:愛光高等学校~全国入試問題解法

単元:
#計算と数の性質#数学(中学生)#中1数学#正の数・負の数#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$168$と$1260$の最大公約数を$x$とする.
$ x$の正の約数をすべてかけ合わせると,$x^y$と表せる.
$x,y$をそれぞれ求めよ.
愛光高校過去問
この動画を見る
$168$と$1260$の最大公約数を$x$とする.
$ x$の正の約数をすべてかけ合わせると,$x^y$と表せる.
$x,y$をそれぞれ求めよ.
愛光高校過去問
【中学数学】高校入試:2022年度神奈川県立高校入試数学大問4(ウ)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
2022年度神奈川県立高校入試数学大問4(ウ)解説していきます.
この動画を見る
2022年度神奈川県立高校入試数学大問4(ウ)解説していきます.
2023高校入試解説8問目 内接円 西大和学園 内接円

単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC∽△PRQ
△PRQ=?
*図は動画内参照
2023西大和学園高等学校
この動画を見る
△ABC∽△PRQ
△PRQ=?
*図は動画内参照
2023西大和学園高等学校
2023高校入試解説7問目 工夫して解け2次方程式 早稲田佐賀

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$(2x -1)^2 + 2x -57 = 0$
2023早稲田佐賀高等学校
この動画を見る
2次方程式を解け
$(2x -1)^2 + 2x -57 = 0$
2023早稲田佐賀高等学校
【ここは無理せず安全に!】因数分解:江戸川学園取手高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ a^2-4b^2+12bc-9c^2$を因数分解しなさい.
江戸川取手高校過去問
この動画を見る
$ a^2-4b^2+12bc-9c^2$を因数分解しなさい.
江戸川取手高校過去問
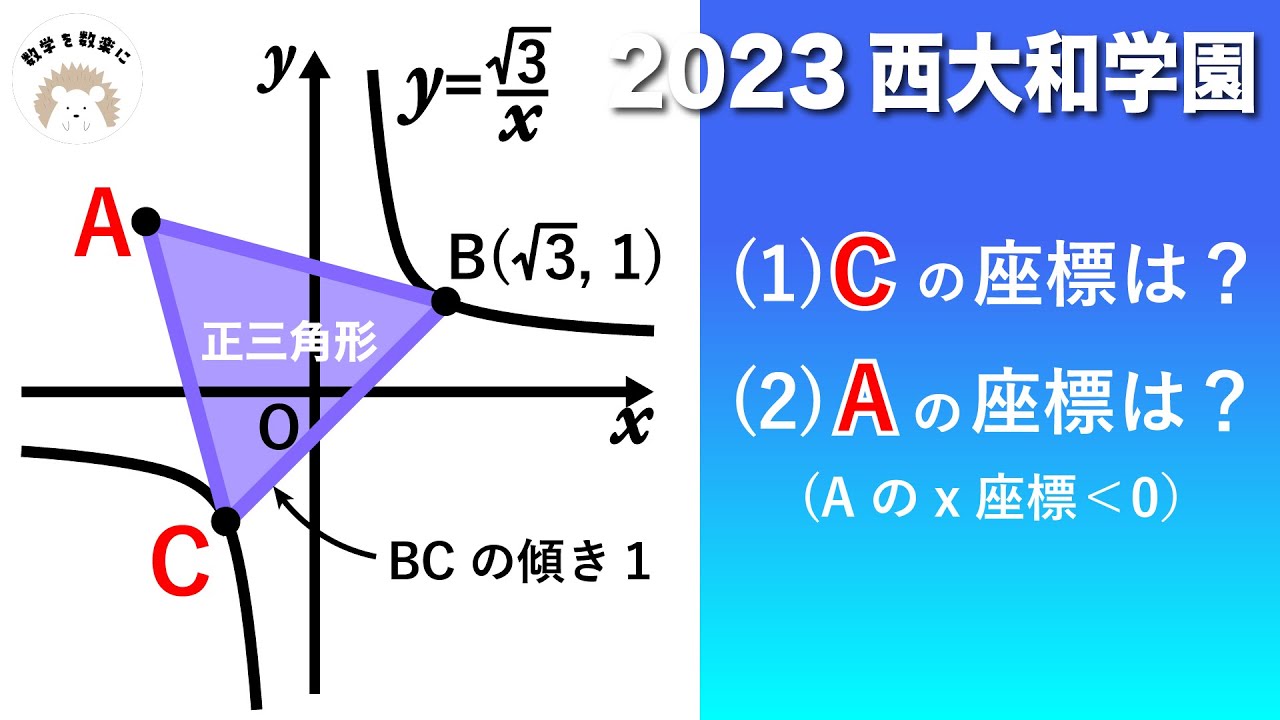
2023高校入試解説6問目 座標平面上の正三角形 西大和学園
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)Cの座標は?
(2)Aの座標は?
(Aのx座標<0)
*図は動画内参照
2023西大和学園高等学校
この動画を見る
(1)Cの座標は?
(2)Aの座標は?
(Aのx座標<0)
*図は動画内参照
2023西大和学園高等学校
2023高校入試解説5問目 2次方程式の応用 西大和学園

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式$x^2 -ax + 1 = 0$の2つの解の差が$\frac{3}{2}$のときa=?
(a>0)
2023西大和学園高等学校
この動画を見る
2次方程式$x^2 -ax + 1 = 0$の2つの解の差が$\frac{3}{2}$のときa=?
(a>0)
2023西大和学園高等学校
【作問者の掌(てのひら)で踊る…!】平方根:城北高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt{2023\times2021-4044+2}$の値を求めよ.
城北高校過去問
この動画を見る
$ \sqrt{2023\times2021-4044+2}$の値を求めよ.
城北高校過去問
2023高校入試解説4問目 もはや高校範囲 西大和学園

単元:
#数学(中学生)#数A#場合の数と確率#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1⃣ 2⃣ 2⃣ 3⃣ 4⃣ 5⃣と書かれたカードがある。
5枚のカードを選んで1列に並べてできる5桁の整数は全部で何通り?
西大和学園高等学校
この動画を見る
1⃣ 2⃣ 2⃣ 3⃣ 4⃣ 5⃣と書かれたカードがある。
5枚のカードを選んで1列に並べてできる5桁の整数は全部で何通り?
西大和学園高等学校
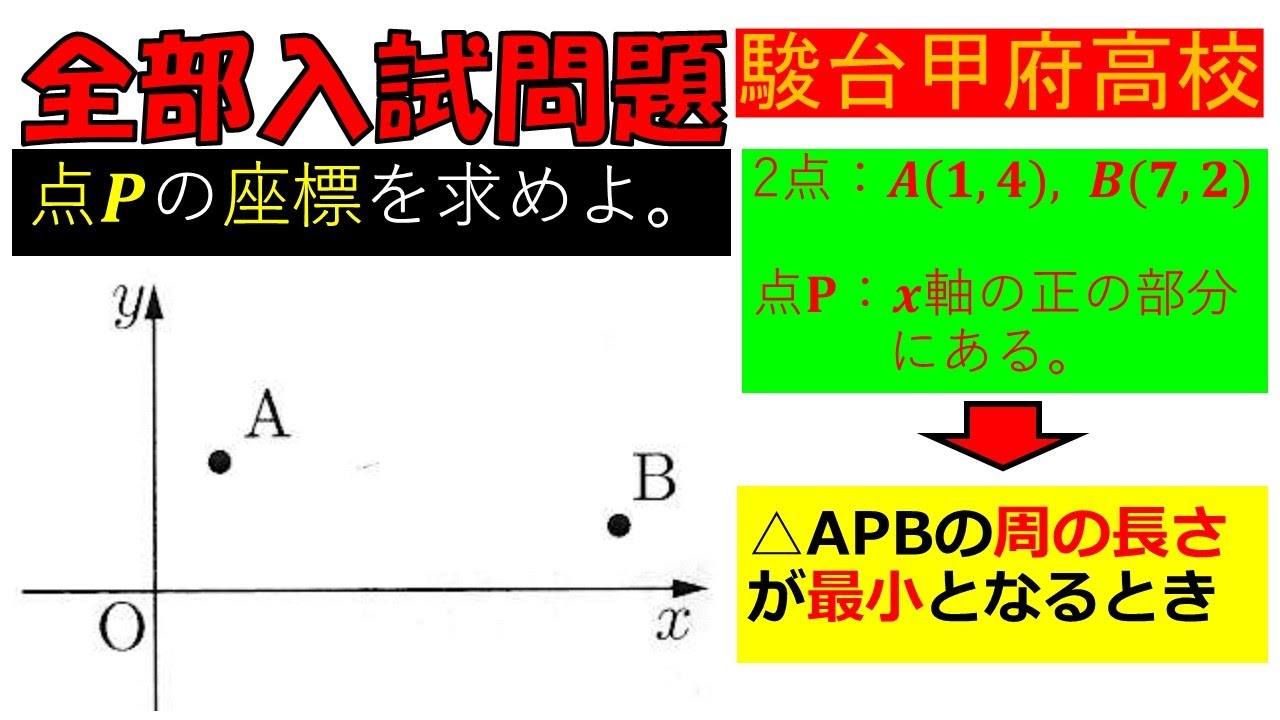
【考え方が大切!一度は挑戦したい。】一次関数:駿台甲府高等学校~全部入試問題
単元:
#数学(中学生)#高校入試過去問(数学)#駿台甲府高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 駿台甲府高等学校
2点:A(1,4), B(7,2)
点P:x軸の正の部分にある。
↓
$\triangle APB$の周の長さ -が最小となるとき
点Pの座標を求めよ。
※図は動画内参照
この動画を見る
入試問題 駿台甲府高等学校
2点:A(1,4), B(7,2)
点P:x軸の正の部分にある。
↓
$\triangle APB$の周の長さ -が最小となるとき
点Pの座標を求めよ。
※図は動画内参照
2023高校入試解説3問目 食塩水 方程式立てずに溶ける!! 等濃度 等量交換 早稲田佐賀

単元:
#数学(中学生)#文章題#売買損益と食塩水#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
食塩水A:5% 80g
食塩水B:7% 120g
食塩水AとBから同量取り出し、A→B、B→Aへ入れるとA,Bの食塩水の濃度が等しくなった。
取り出した食塩水の量は?
2023早稲田佐賀高等学校
この動画を見る
食塩水A:5% 80g
食塩水B:7% 120g
食塩水AとBから同量取り出し、A→B、B→Aへ入れるとA,Bの食塩水の濃度が等しくなった。
取り出した食塩水の量は?
2023早稲田佐賀高等学校
2023高校入試解説2問目 文字でおけ! 早稲田佐賀

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$2023 \times 108 -2022 \times 110 +4046 -54$
2023早稲田佐賀高等学校
この動画を見る
$2023 \times 108 -2022 \times 110 +4046 -54$
2023早稲田佐賀高等学校
