 高校入試過去問(数学)
高校入試過去問(数学)
 高校入試過去問(数学)
高校入試過去問(数学)
【初手で失敗したくない!計算量を減らす工夫】整数:東京工業大学附属科学技術高等学校~全部入試問題

単元:
#数学(中学生)#高校入試過去問(数学)#東京工業大学附属科学技術高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京工業大学附属科学技術高等学校
正の整数について、次の問いに答えなさい。
2つの続いた奇数の平方の和は、それら2つの奇数の和の10倍に50を加えた値と等しい。
このとき、2つの続いた奇数のうち、 小さいほうの数を求めなさい。
この動画を見る
入試問題 東京工業大学附属科学技術高等学校
正の整数について、次の問いに答えなさい。
2つの続いた奇数の平方の和は、それら2つの奇数の和の10倍に50を加えた値と等しい。
このとき、2つの続いた奇数のうち、 小さいほうの数を求めなさい。
三角形の面積三等分!!巣鴨高校
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
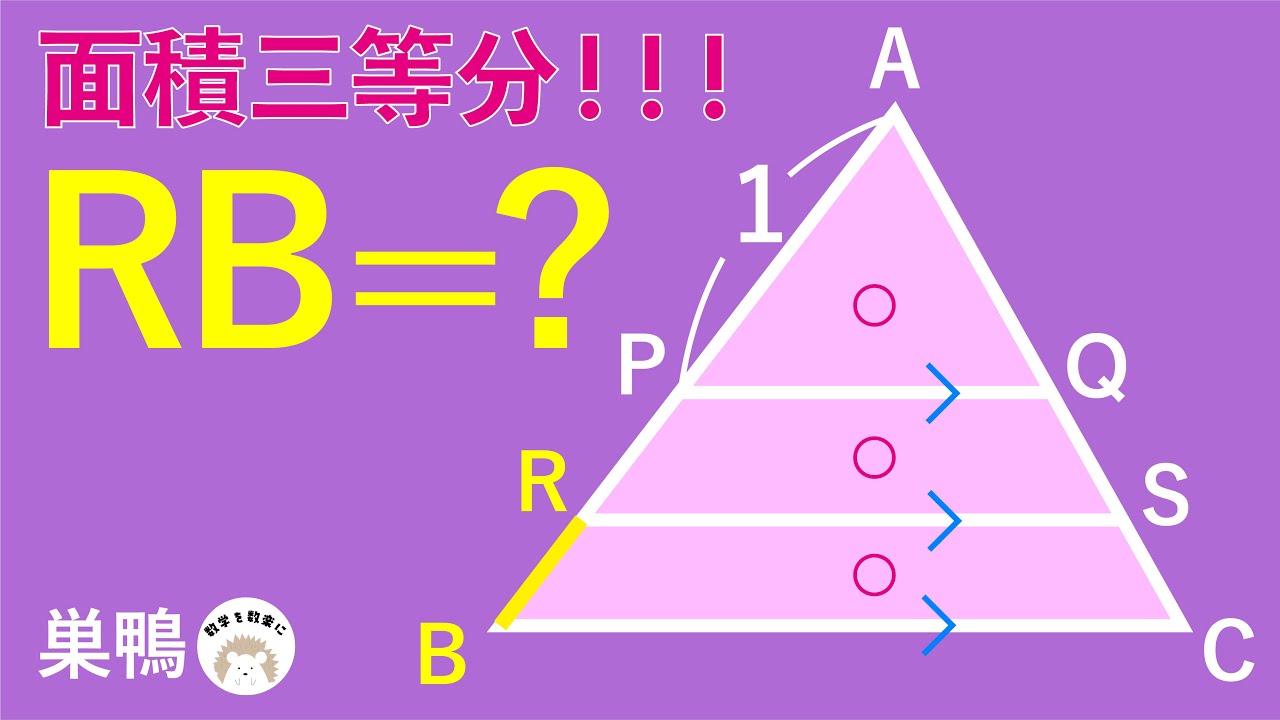
面積三等分
RB=?
*図は動画内参照
巣鴨高等学校
この動画を見る
面積三等分
RB=?
*図は動画内参照
巣鴨高等学校
こう見えても慶應義塾

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数A#数と式#場合の数と確率#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
絶対値が2になる数と49の平方根の和は何通り?
慶應義塾高等学校
この動画を見る
絶対値が2になる数と49の平方根の和は何通り?
慶應義塾高等学校
文中に2022を含む予想問題~全部入試問題

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試予想問題【西暦】
$20 \times 21 \times 22 \times 23 + 1=m^2$
を満たす正の整数$m$を求めよ。
この動画を見る
入試予想問題【西暦】
$20 \times 21 \times 22 \times 23 + 1=m^2$
を満たす正の整数$m$を求めよ。
【中学数学】立命館高校の過去問~ぜひチャレンジしてね~【高校受験】

単元:
#数学(中学生)#高校入試過去問(数学)#立命館高等学校
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
正の数$a$に対して、ある操作を行って得られる値を記号$\langle\langle \rangle \rangle$を使って、$\langle \langle a \rangle \rangle$と表します。
この操作において,$\langle \langle a \rangle \rangle =0$となるのは、$a=1$ときのみ、$\langle \langle a \rangle \rangle =1$となるのは、$a=10$のときのみと約束します。
また、この操作は2つの正の数$a,b$に対して、$\langle \langle a \times b \rangle \rangle =\langle \langle a\rangle \rangle +\langle \langle b\rangle \rangle ,\langle \langle \displaystyle \frac{1}{a} \rangle \rangle =-\langle \langle a \rangle \rangle$という性質があります。
このとき、次の問いに答えよ。
(1)$\langle \langle \displaystyle \frac{y}{x} \rangle \rangle$を$\langle \langle x \rangle \rangle$と$\langle \langle y \rangle \rangle$を用いて表せ。
ただし、$x,y$は正の数である
(2)$\langle \langle 1000 \rangle \rangle$の値を整数で答えよ
この動画を見る
正の数$a$に対して、ある操作を行って得られる値を記号$\langle\langle \rangle \rangle$を使って、$\langle \langle a \rangle \rangle$と表します。
この操作において,$\langle \langle a \rangle \rangle =0$となるのは、$a=1$ときのみ、$\langle \langle a \rangle \rangle =1$となるのは、$a=10$のときのみと約束します。
また、この操作は2つの正の数$a,b$に対して、$\langle \langle a \times b \rangle \rangle =\langle \langle a\rangle \rangle +\langle \langle b\rangle \rangle ,\langle \langle \displaystyle \frac{1}{a} \rangle \rangle =-\langle \langle a \rangle \rangle$という性質があります。
このとき、次の問いに答えよ。
(1)$\langle \langle \displaystyle \frac{y}{x} \rangle \rangle$を$\langle \langle x \rangle \rangle$と$\langle \langle y \rangle \rangle$を用いて表せ。
ただし、$x,y$は正の数である
(2)$\langle \langle 1000 \rangle \rangle$の値を整数で答えよ
キレイに解けます 立命館高校
単元:
#数学(中学生)#中2数学#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
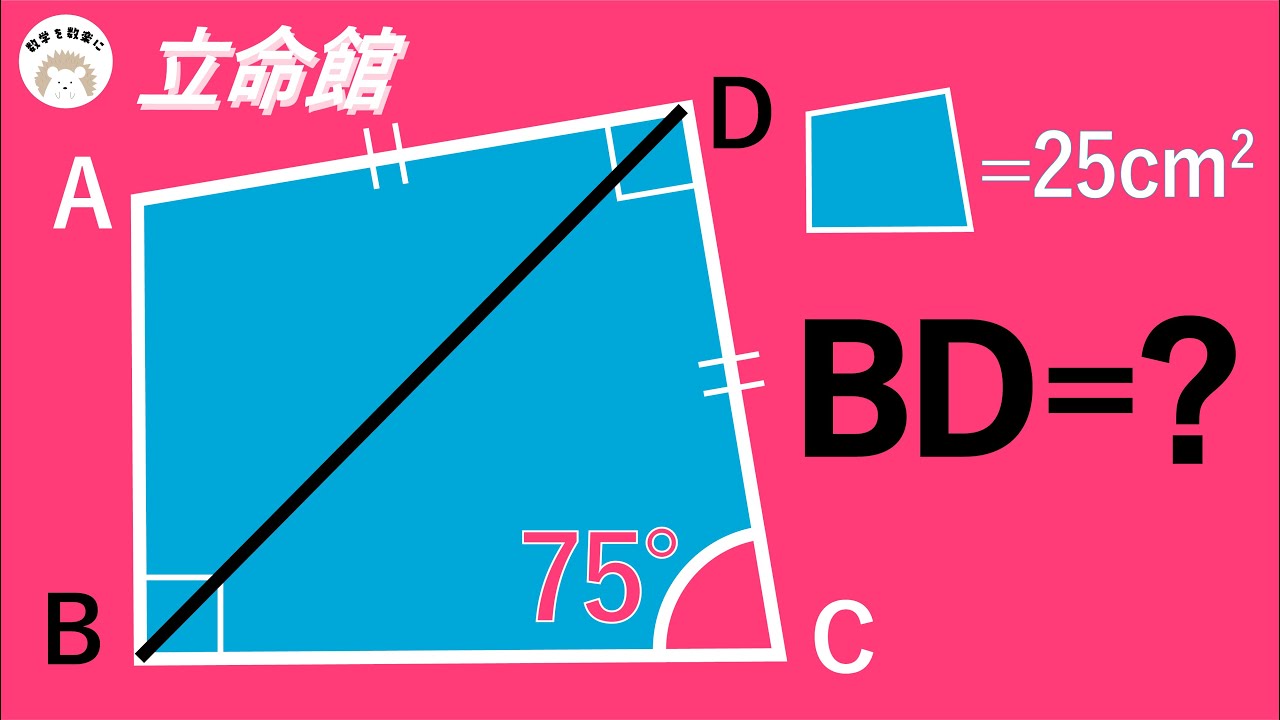
四角形ABCD=25㎠のとき
BD=?
*図は動画内参照
立命館高等学校
この動画を見る
四角形ABCD=25㎠のとき
BD=?
*図は動画内参照
立命館高等学校
文中に2022を含む予想問題(その2)~全部入試問題

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$N=2022-\sqrt{ 218 }$
とする。
$N$が整数となるとき、$N$の絶対値の 最小値を求めなさい。
※ただし、$x$は自然数である。
この動画を見る
$N=2022-\sqrt{ 218 }$
とする。
$N$が整数となるとき、$N$の絶対値の 最小値を求めなさい。
※ただし、$x$は自然数である。
小学生も解ける!! 名古屋高校
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
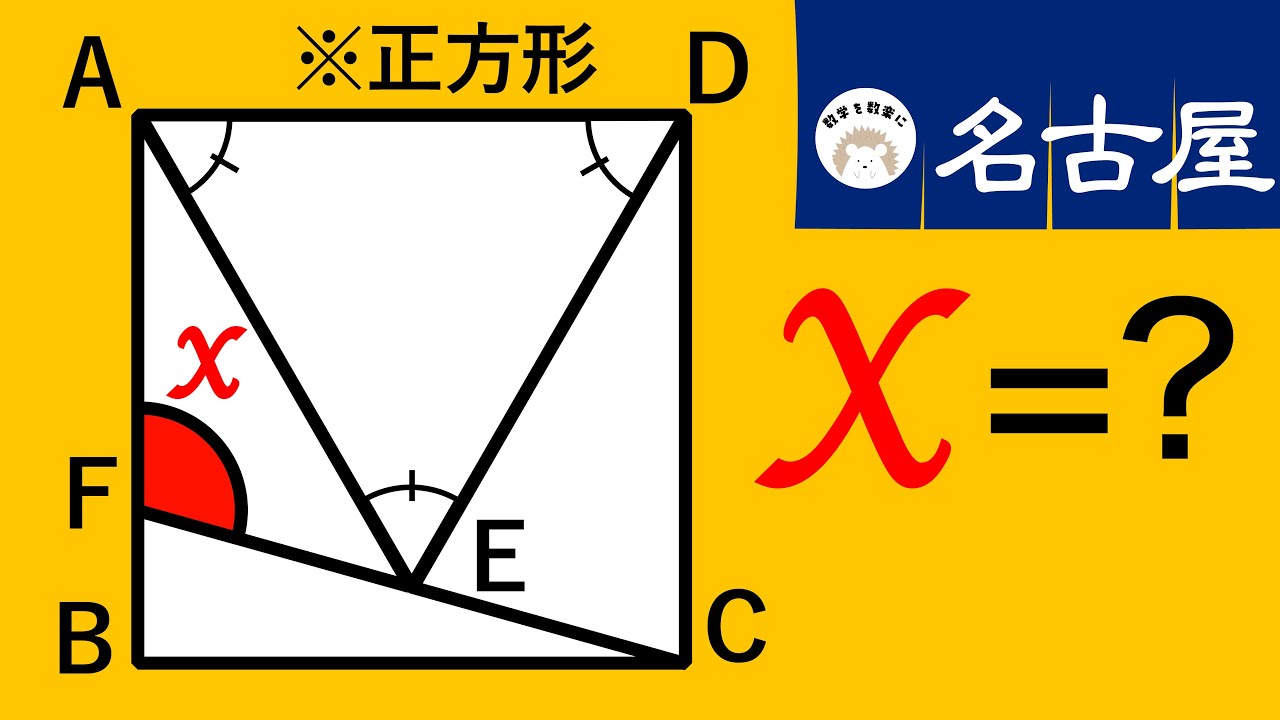
正方形
$\angle x=?$
*図は動画内参照
名古屋高等学校
この動画を見る
正方形
$\angle x=?$
*図は動画内参照
名古屋高等学校
文中に2022を含む予想問題(その1)

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
以下の問いに答えよ。
$\displaystyle \frac{5}{7}$を小数で表すとき、
小数第2022位の数を求めよ。
この動画を見る
以下の問いに答えよ。
$\displaystyle \frac{5}{7}$を小数で表すとき、
小数第2022位の数を求めよ。
この問題は嫌いです 慶應義塾

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(1-\sqrt 6)^2 - (\sqrt 2 - \sqrt 3)^2$
慶應義塾高等学校
この動画を見る
$(1-\sqrt 6)^2 - (\sqrt 2 - \sqrt 3)^2$
慶應義塾高等学校
問題文に2022を含む予想問題(考察編)~全部入試問題

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
西暦問題
次の入試問題を導け
$2022=?$
この動画を見る
西暦問題
次の入試問題を導け
$2022=?$
2次方程式の応用 明大明治

単元:
#数学(中学生)#中3数学#平方根#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式$x^2-6x+p=0$の2つの解の差が$2 \sqrt 3$のとき
p=?
明治大学付属明治高等学校
この動画を見る
2次方程式$x^2-6x+p=0$の2つの解の差が$2 \sqrt 3$のとき
p=?
明治大学付属明治高等学校
【ケアレスミスをなくす3分間!】連立方程式:久留米大学附設高等学校~全部入試問題

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)#久留米大学附設高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 久留米大学附設高等学校
【連立方程式】
aの値を求めよ。
$\begin{eqnarray}
\begin{cases}
8x-y=5 & \\
ax+5y=7 &
\end{cases}
\end{eqnarray}$
の解を$x=m,y=n$とするとき
$2m-n=1$が成り立つ
この動画を見る
入試問題 久留米大学附設高等学校
【連立方程式】
aの値を求めよ。
$\begin{eqnarray}
\begin{cases}
8x-y=5 & \\
ax+5y=7 &
\end{cases}
\end{eqnarray}$
の解を$x=m,y=n$とするとき
$2m-n=1$が成り立つ
数学を数楽にして解く 2通りで解説 専修大学松戸
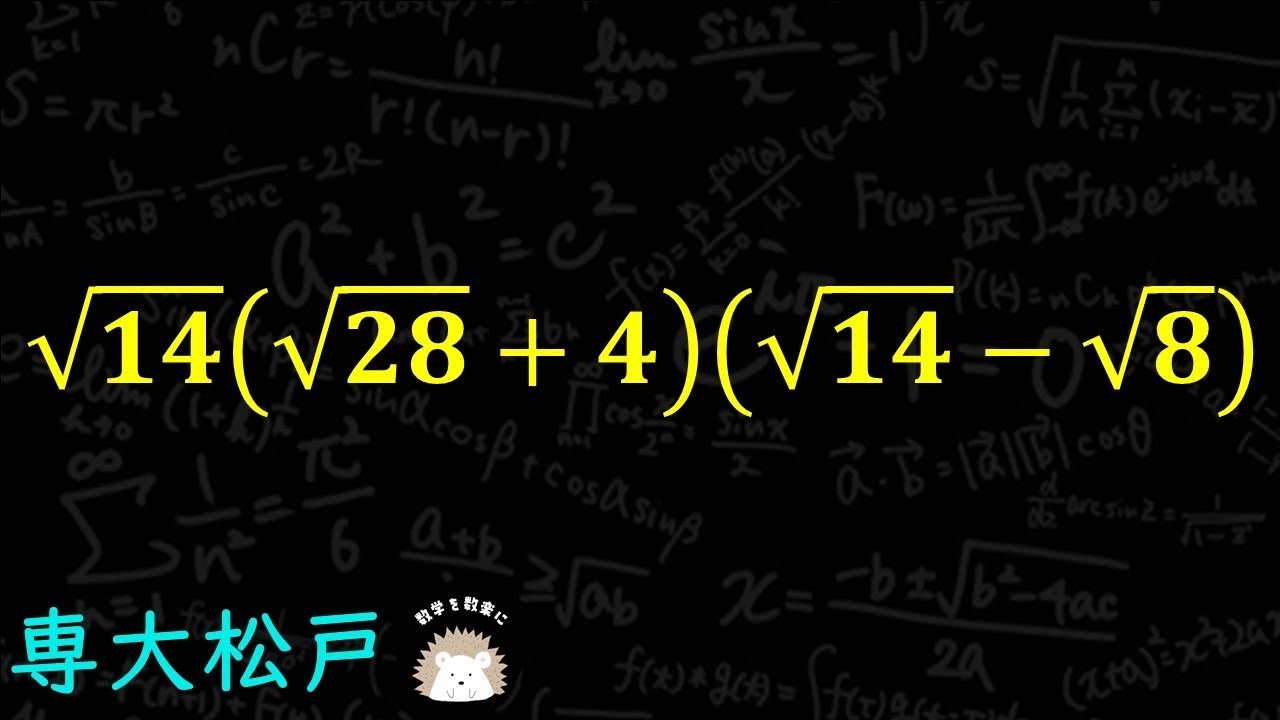
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{14}(\sqrt{28}+4)(\sqrt{14} - \sqrt 8)$
専修大学松戸高等学校
この動画を見る
$\sqrt{14}(\sqrt{28}+4)(\sqrt{14} - \sqrt 8)$
専修大学松戸高等学校
二次関数:日本大学第三高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#日本大学第三高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日本大学第三高等学校
放物線$y = ax^2 (a \gt 0)$ 上に$2$点$A$と$B$。
点$A:(-2,8)$
点$B:x$座標が$3$
点$C:$直線$AB$と$y$軸の交点
(1)$a$の値を求めなさい。
(2)直線$AB$の式を求めなさい。
この動画を見る
入試問題 日本大学第三高等学校
放物線$y = ax^2 (a \gt 0)$ 上に$2$点$A$と$B$。
点$A:(-2,8)$
点$B:x$座標が$3$
点$C:$直線$AB$と$y$軸の交点
(1)$a$の値を求めなさい。
(2)直線$AB$の式を求めなさい。
【基礎力、秒殺、先見性】計算:國學院大學久我山高等学校~全部入試問題

単元:
#数学(中学生)#高校入試過去問(数学)#國學院大學久我山高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 國學院大學久我山高等学校
次の▬を適当にうめなさい。
$2-2 \div 2\div2 \times 2^2 +2=$▬
$\displaystyle \frac{2x-7}{6}-\displaystyle \frac{2x+1}{3}+\displaystyle \frac{4x-1}{2}=$▬
この動画を見る
入試問題 國學院大學久我山高等学校
次の▬を適当にうめなさい。
$2-2 \div 2\div2 \times 2^2 +2=$▬
$\displaystyle \frac{2x-7}{6}-\displaystyle \frac{2x+1}{3}+\displaystyle \frac{4x-1}{2}=$▬
【この考え方が高2の内容に繋がる!】関数:江戸川学園取手高等学校~全部入試問題

単元:
#数学(中学生)#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 江戸川学園取手高等学校
$y-5$は$x-2$の2乗に 比例する関数であり、
$x =1$のとき$y =7$である。
$x$が$1$から$4$まで増加するときの変化の割合を求めなさい。
この動画を見る
入試問題 江戸川学園取手高等学校
$y-5$は$x-2$の2乗に 比例する関数であり、
$x =1$のとき$y =7$である。
$x$が$1$から$4$まで増加するときの変化の割合を求めなさい。
平方根 小数部分 成城学園

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2 \sqrt 3$の小数部分をaとするとき
$a^2+6a-16=?$
成城学園高等学校
この動画を見る
$2 \sqrt 3$の小数部分をaとするとき
$a^2+6a-16=?$
成城学園高等学校
【出題されてもひるまないための3分間!】文字式:愛光高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#愛光高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 愛光高等学校
▬に適する数式を記入せよ。
$\displaystyle \frac{15}{7}a^12 \times (-\displaystyle \frac{14}{5a^2}) \div (-3a^2)-\displaystyle \frac{7}{15}a^2 \div \displaystyle \frac{21}{40}a=$▬
この動画を見る
入試問題 愛光高等学校
▬に適する数式を記入せよ。
$\displaystyle \frac{15}{7}a^12 \times (-\displaystyle \frac{14}{5a^2}) \div (-3a^2)-\displaystyle \frac{7}{15}a^2 \div \displaystyle \frac{21}{40}a=$▬
【1分で理解!3分で完答!】関数:近畿大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#近畿大学付属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
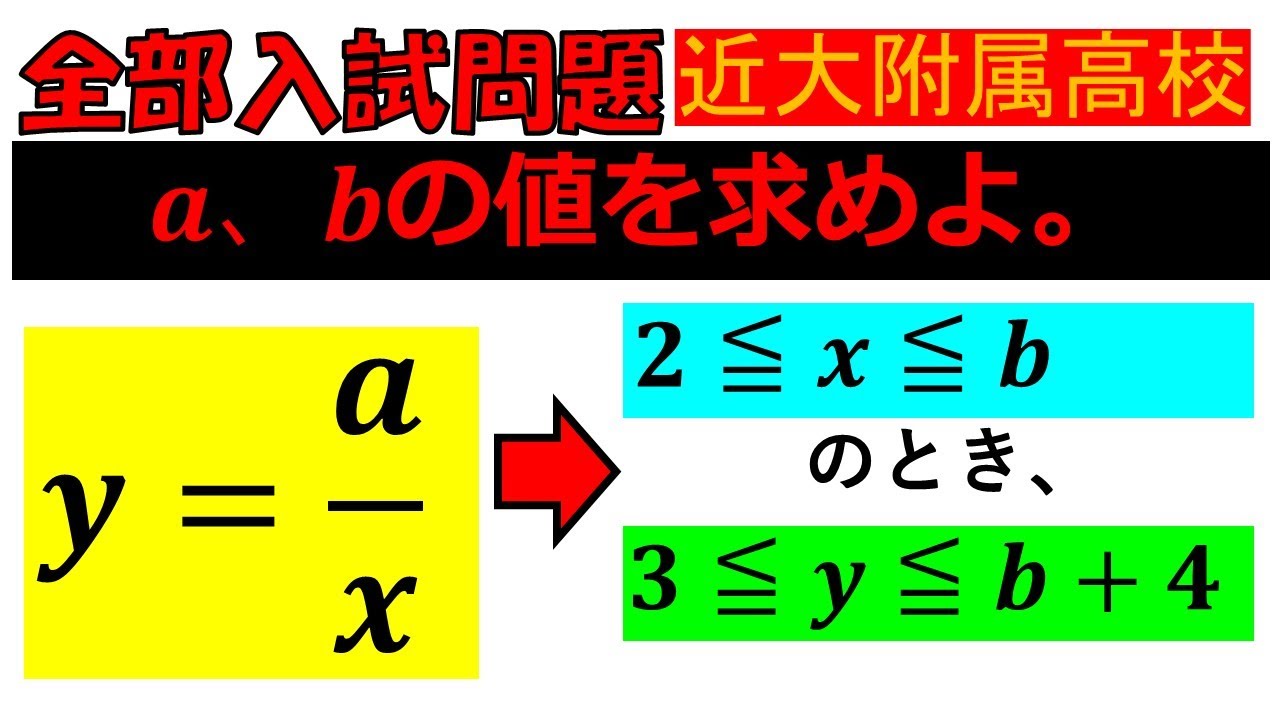
入試問題 近畿大学附属高等学校
a、bの値を求めよ。
$y=\displaystyle \frac{a}{x}$
↓
$2 \leqq x \leqq b$のとき、
$3 \leqq y \leqq b+4$
この動画を見る
入試問題 近畿大学附属高等学校
a、bの値を求めよ。
$y=\displaystyle \frac{a}{x}$
↓
$2 \leqq x \leqq b$のとき、
$3 \leqq y \leqq b+4$
相似より〇〇を見つける方が難しい 大阪星光学院(改)
単元:
#数学(中学生)#中2数学#中3数学#相似な図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
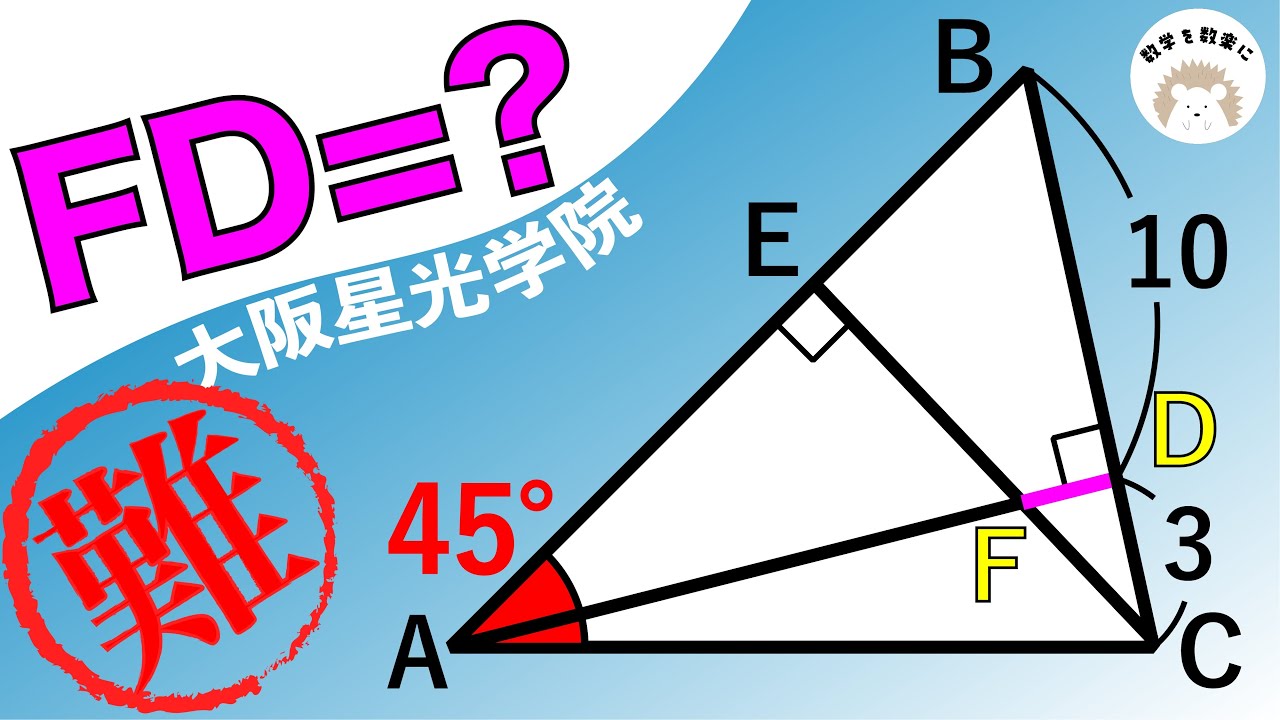
FD=?
*図は動画内参照
大阪星光学院高等学校
この動画を見る
FD=?
*図は動画内参照
大阪星光学院高等学校
1271を素因数分解 大阪教育大附属天王寺

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$36^2=1296$
$1271$を素数の積で表せ
大阪教育大学附属高等学校天王寺校舎
この動画を見る
$36^2=1296$
$1271$を素数の積で表せ
大阪教育大学附属高等学校天王寺校舎
高校受験でも軌跡の問題あります。滝高校
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
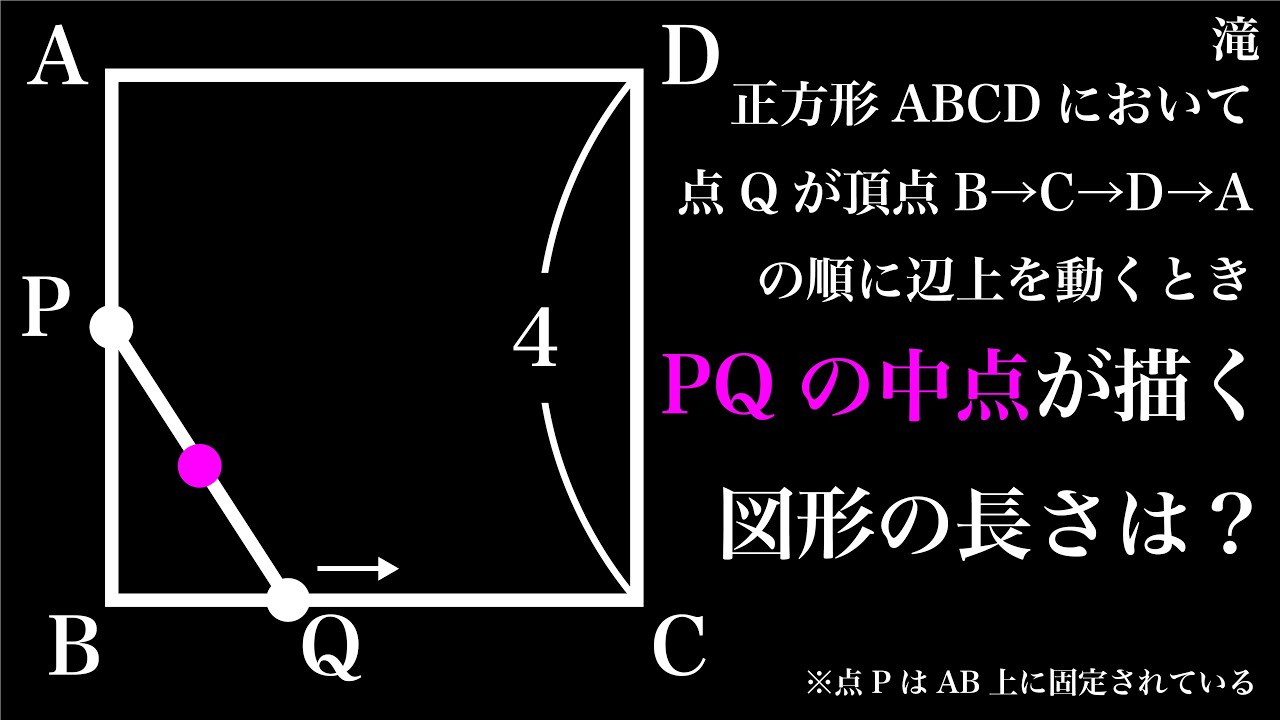
正方形ABCDにおいて点Qが頂点B→C→D→Aの順に辺上を動くとき
PQの中点が描く図形の長さは?
*図は動画内参照
滝高等学校
この動画を見る
正方形ABCDにおいて点Qが頂点B→C→D→Aの順に辺上を動くとき
PQの中点が描く図形の長さは?
*図は動画内参照
滝高等学校
【まず、2分!手段は、いろいろ身に付けよう!】因数分解:江戸川学園取手高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 江戸川学園取手高等学校
因数分解をしなさい。
$x^2-6xy+9y^2+3x-9y+2$
この動画を見る
入試問題 江戸川学園取手高等学校
因数分解をしなさい。
$x^2-6xy+9y^2+3x-9y+2$
高校入試だけど二重根号
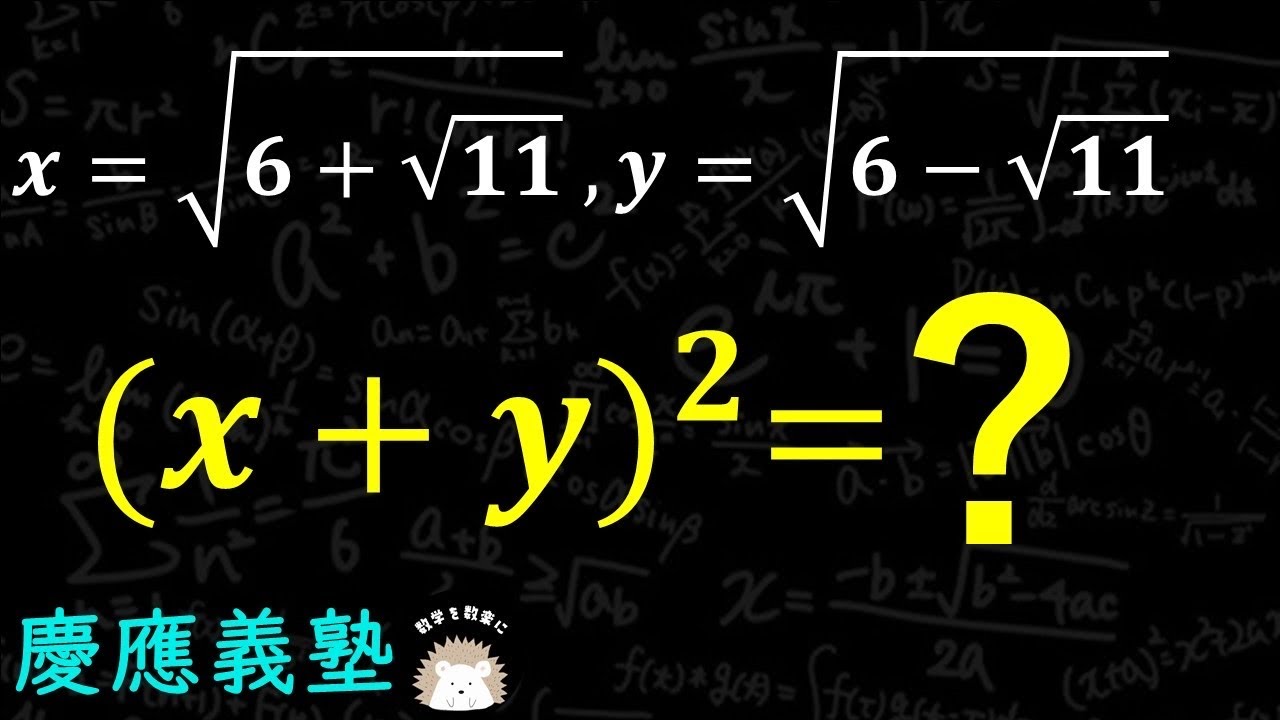
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=\sqrt{6+\sqrt{11}} , y=\sqrt{6-\sqrt{11}} $
$(x+y)^2 = ?$
慶應義塾高等学校
この動画を見る
$x=\sqrt{6+\sqrt{11}} , y=\sqrt{6-\sqrt{11}} $
$(x+y)^2 = ?$
慶應義塾高等学校
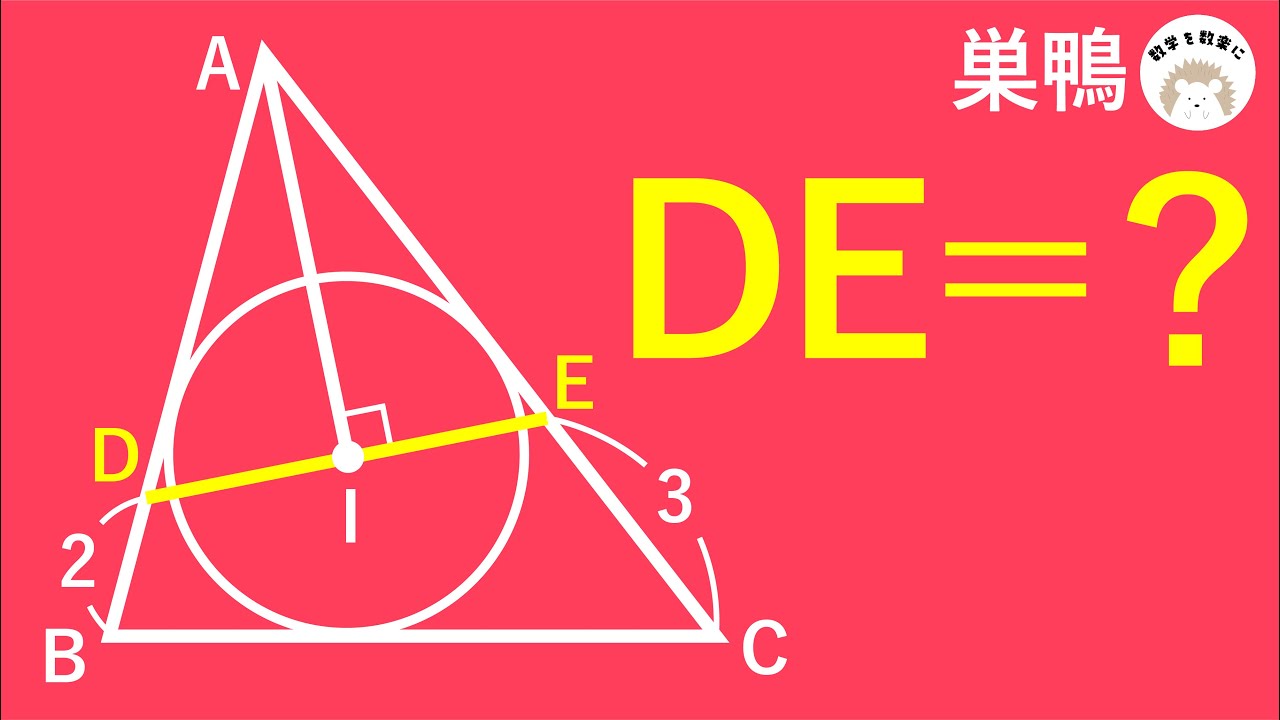
あなたにとって難問かもしれません。巣鴨
気持ち良く解こう!! 成城学園

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{54}(3a+3b)(9a-9b)(2a^2+2b^2)$
成城学園高等学校
この動画を見る
$\frac{1}{54}(3a+3b)(9a-9b)(2a^2+2b^2)$
成城学園高等学校
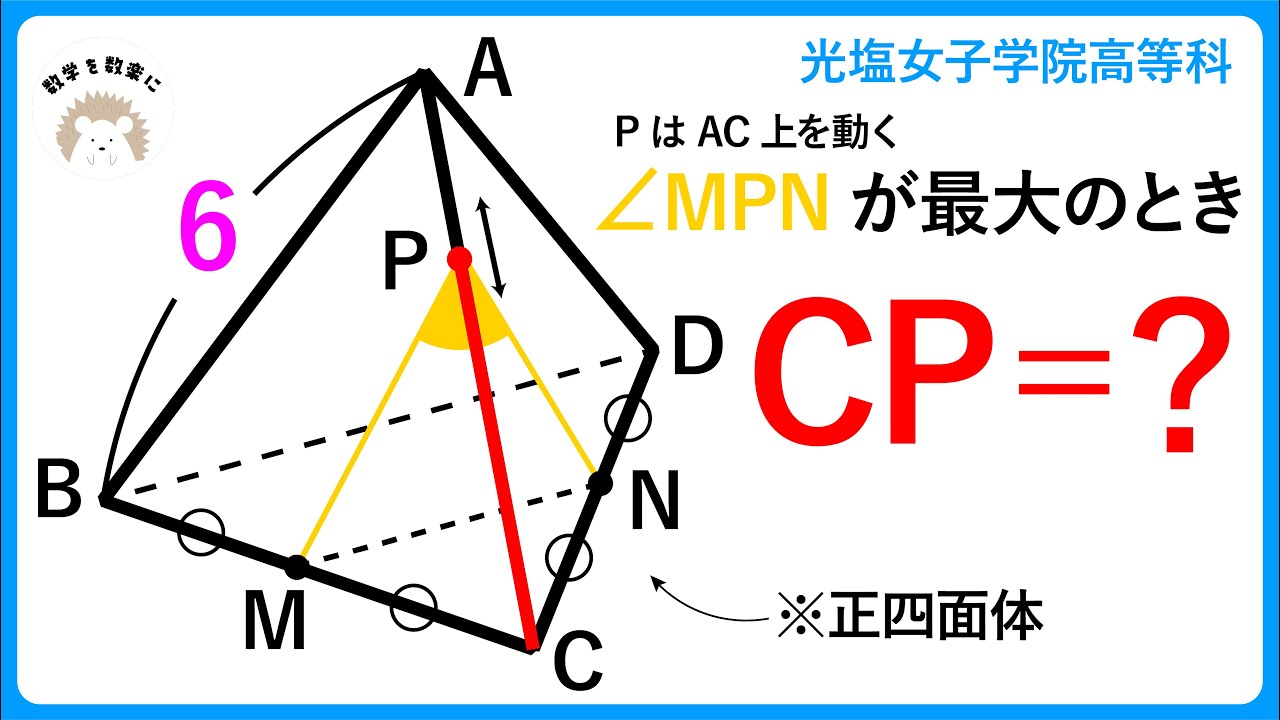
良問!!立体図形 角が最大になるとき
単元:
#数学(中学生)#立体図形#立体切断#立体図形その他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
正四面体
$\angle MPN$が最大のとき
CP=?
*図は動画内参照
光塩女子学院高等科
この動画を見る
正四面体
$\angle MPN$が最大のとき
CP=?
*図は動画内参照
光塩女子学院高等科
分数の中に分数 慶應義塾高校

単元:
#数学(中学生)#数Ⅱ#式と証明#整式の除法・分数式・二項定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{\frac{1}{3} - \frac{2}{5} }
{\frac{1}{3} - \frac{2}{5} + \frac{3}{7}}$
慶應義塾高等学校
この動画を見る
$\frac{\frac{1}{3} - \frac{2}{5} }
{\frac{1}{3} - \frac{2}{5} + \frac{3}{7}}$
慶應義塾高等学校
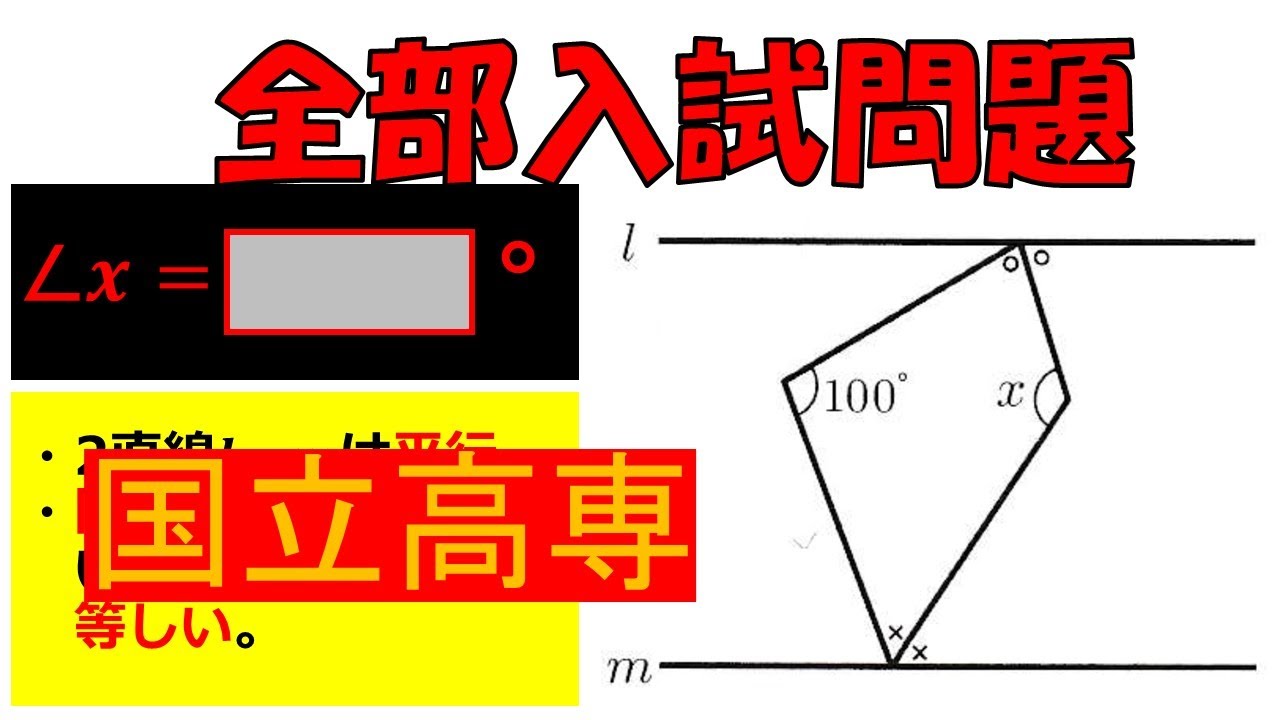
【まず3分!小学校から中学までの全知識!】図形:国立高等専門学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#国立高等専門学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 国立高等専門学校
・2直線l、mは平行。
・同じ印の付けられて いる角がそれぞれ 等しい。
$\angle x=$▬°
$x$の角度を求めよ。
この動画を見る
入試問題 国立高等専門学校
・2直線l、mは平行。
・同じ印の付けられて いる角がそれぞれ 等しい。
$\angle x=$▬°
$x$の角度を求めよ。
