 立命館高等学校
立命館高等学校
 立命館高等学校
立命館高等学校
integer problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study

単元:
#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$2104^2を11で割った余りを求めなさい$
この動画を見る
$2104^2を11で割った余りを求めなさい$
【成功をつかめ…!】一次方程式:立命館高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#方程式#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$4x-3(x-\dfrac{2-5x}{7})=\dfrac{8x-1}{3}$
$を解きなさい。$
この動画を見る
$4x-3(x-\dfrac{2-5x}{7})=\dfrac{8x-1}{3}$
$を解きなさい。$
【それって、つまり…!】整数:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 立命館高等学校
1から30までのすべての整数の積は・・・
一の位から何個連続で0が並ぶか。
[つまり、 1×2×3×…×28×29×30 ということ!]
この動画を見る
入試問題 立命館高等学校
1から30までのすべての整数の積は・・・
一の位から何個連続で0が並ぶか。
[つまり、 1×2×3×…×28×29×30 ということ!]
【スマートに行こう…!】因数分解:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (2x+3y)^2-3(x-3y)\times (x+3y)-4y^2 $
を因数分解しなさい.
立命館高校過去問
この動画を見る
$ (2x+3y)^2-3(x-3y)\times (x+3y)-4y^2 $
を因数分解しなさい.
立命館高校過去問
【まず手を動かせ!】整数:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 2104^2 $を11で割った余りを求めなさい.
立命館高校過去問
この動画を見る
$ 2104^2 $を11で割った余りを求めなさい.
立命館高校過去問
【正しい攻め方をしないと…】因数分解:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$xy^2-xz^2+2xz-x$を因数分解しなさい.
立命館高校過去問
この動画を見る
$xy^2-xz^2+2xz-x$を因数分解しなさい.
立命館高校過去問
【中学数学】立命館高校の過去問~ぜひチャレンジしてね~【高校受験】

単元:
#数学(中学生)#高校入試過去問(数学)#立命館高等学校
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
正の数$a$に対して、ある操作を行って得られる値を記号$\langle\langle \rangle \rangle$を使って、$\langle \langle a \rangle \rangle$と表します。
この操作において,$\langle \langle a \rangle \rangle =0$となるのは、$a=1$ときのみ、$\langle \langle a \rangle \rangle =1$となるのは、$a=10$のときのみと約束します。
また、この操作は2つの正の数$a,b$に対して、$\langle \langle a \times b \rangle \rangle =\langle \langle a\rangle \rangle +\langle \langle b\rangle \rangle ,\langle \langle \displaystyle \frac{1}{a} \rangle \rangle =-\langle \langle a \rangle \rangle$という性質があります。
このとき、次の問いに答えよ。
(1)$\langle \langle \displaystyle \frac{y}{x} \rangle \rangle$を$\langle \langle x \rangle \rangle$と$\langle \langle y \rangle \rangle$を用いて表せ。
ただし、$x,y$は正の数である
(2)$\langle \langle 1000 \rangle \rangle$の値を整数で答えよ
この動画を見る
正の数$a$に対して、ある操作を行って得られる値を記号$\langle\langle \rangle \rangle$を使って、$\langle \langle a \rangle \rangle$と表します。
この操作において,$\langle \langle a \rangle \rangle =0$となるのは、$a=1$ときのみ、$\langle \langle a \rangle \rangle =1$となるのは、$a=10$のときのみと約束します。
また、この操作は2つの正の数$a,b$に対して、$\langle \langle a \times b \rangle \rangle =\langle \langle a\rangle \rangle +\langle \langle b\rangle \rangle ,\langle \langle \displaystyle \frac{1}{a} \rangle \rangle =-\langle \langle a \rangle \rangle$という性質があります。
このとき、次の問いに答えよ。
(1)$\langle \langle \displaystyle \frac{y}{x} \rangle \rangle$を$\langle \langle x \rangle \rangle$と$\langle \langle y \rangle \rangle$を用いて表せ。
ただし、$x,y$は正の数である
(2)$\langle \langle 1000 \rangle \rangle$の値を整数で答えよ
【奇問認定!?】関数:立命館高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
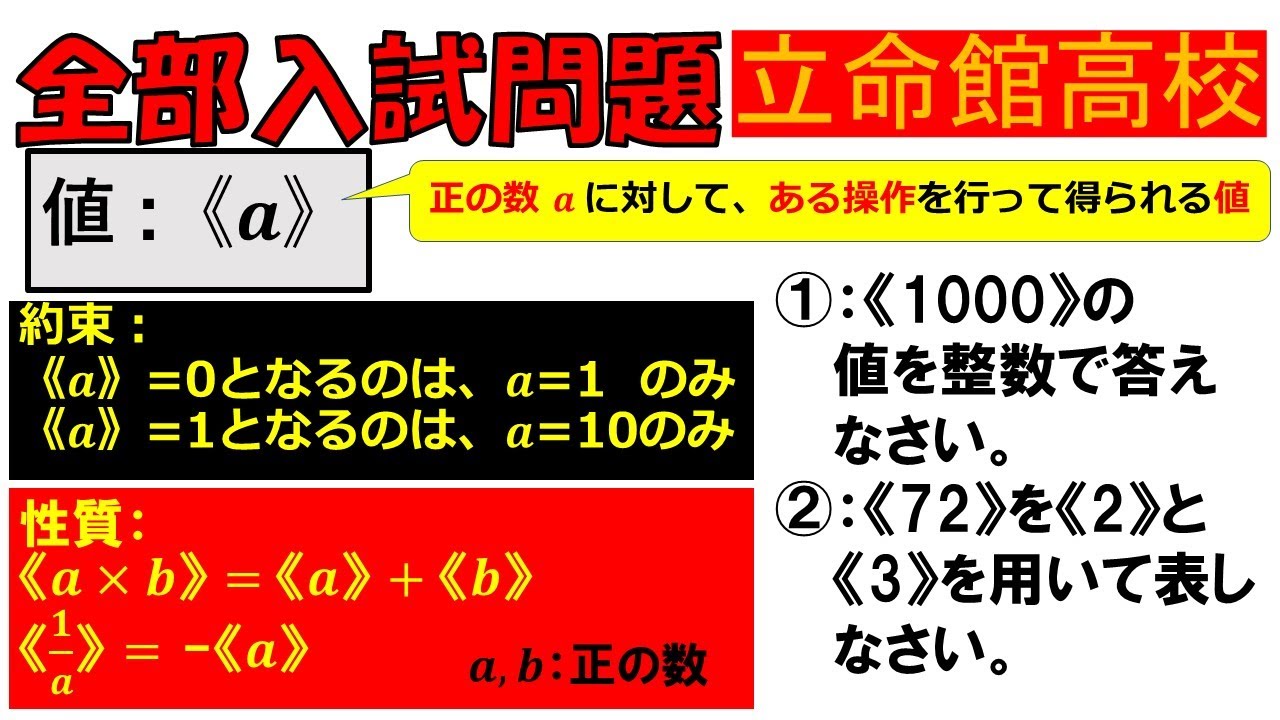
入試問題 立命館高等学校
値:《a》
正の数に対して、ある操作を行って得られる値
【約束:】
《a》=0となるのは、a=1 のみ
《a》 =1となるのは、a=10のみ
【性質:】
《a×b》 = 《a》+ 《b》 《$\displaystyle \frac{1}{a}$》 = -《a》
a, b: 正の数
①:《1000》の 値を整数で答えなさい。
②: 《72》を《2》と《3》を用いて表し なさい
この動画を見る
入試問題 立命館高等学校
値:《a》
正の数に対して、ある操作を行って得られる値
【約束:】
《a》=0となるのは、a=1 のみ
《a》 =1となるのは、a=10のみ
【性質:】
《a×b》 = 《a》+ 《b》 《$\displaystyle \frac{1}{a}$》 = -《a》
a, b: 正の数
①:《1000》の 値を整数で答えなさい。
②: 《72》を《2》と《3》を用いて表し なさい
【3分でOK!定石を身に付ける!】計算:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 立命館高等学校
【西暦を含む数学問題】 計算しなさい。
$2021 \times 2019 - 2018^2 - 2020 \times 2023 + 2019^2 +2020$
この動画を見る
入試問題 立命館高等学校
【西暦を含む数学問題】 計算しなさい。
$2021 \times 2019 - 2018^2 - 2020 \times 2023 + 2019^2 +2020$
方程式:立命館高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 立命館高等学校
$a ★ b = a^2-b^2+2ab$ と定める。
$x ★(x + 4) = 0$ を解きなさい。
この動画を見る
入試問題 立命館高等学校
$a ★ b = a^2-b^2+2ab$ と定める。
$x ★(x + 4) = 0$ を解きなさい。
連立方程式:立命館高校入試~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 立命館高等学校
次の連立方程式を解きなさい。
$\displaystyle \frac{x+3y}{2}=\displaystyle \frac{2x+6y+2}{3}=-\displaystyle \frac{2}{5}(4x+5y)$
この動画を見る
入試問題 立命館高等学校
次の連立方程式を解きなさい。
$\displaystyle \frac{x+3y}{2}=\displaystyle \frac{2x+6y+2}{3}=-\displaystyle \frac{2}{5}(4x+5y)$
平方根の計算!!(2019立命館)
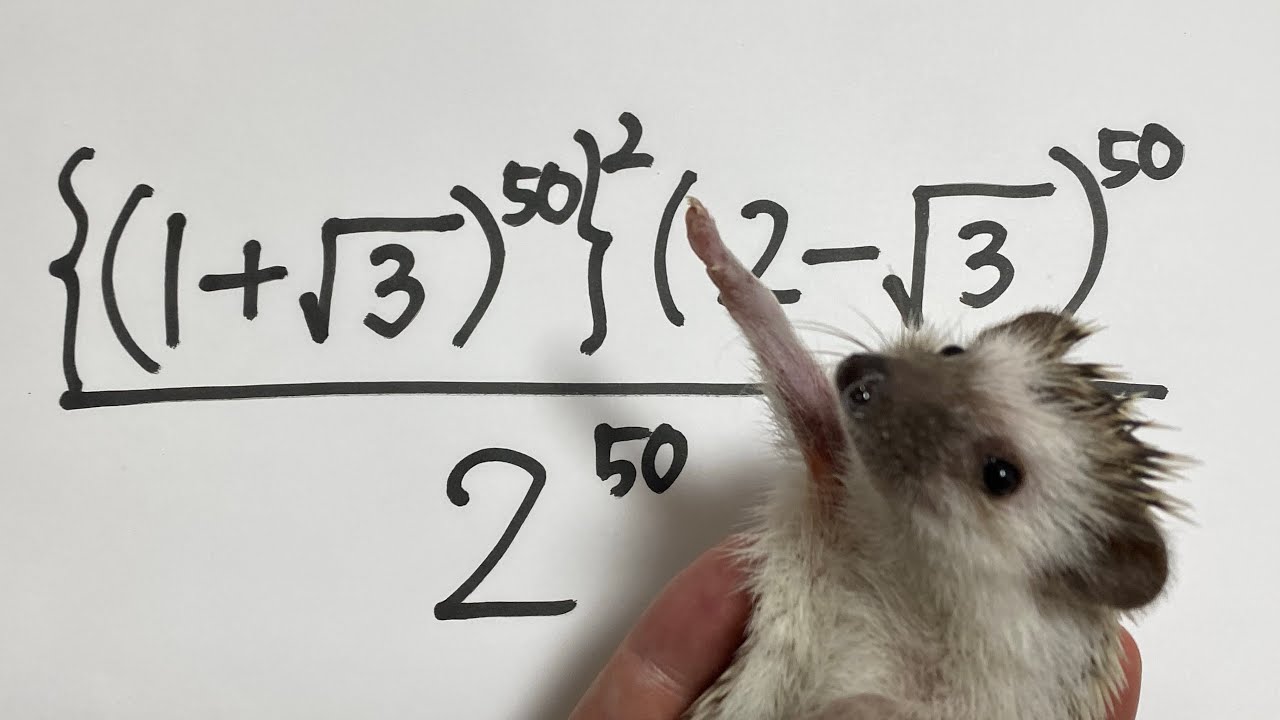
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#立命館高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
以下を計算せよ
$\displaystyle \frac{\{(1+\sqrt{ 3 })^{50}\}^2(2-\sqrt{ 3 })^{50}}{2^{50}}$
出典:2019年立命館大学
この動画を見る
以下を計算せよ
$\displaystyle \frac{\{(1+\sqrt{ 3 })^{50}\}^2(2-\sqrt{ 3 })^{50}}{2^{50}}$
出典:2019年立命館大学
