 平面図形
平面図形
 平面図形
平面図形
【高校受験対策/数学】死守71

単元:
#数学(中学生)#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#平方根#比例・反比例#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守71
①$8÷4+6$を計算せよ。
②$\frac{1}{2}+\frac{9}{10}×\frac{5}{3}$を計算せよ。
④$y$は$x$に反比例し、$x=2$のとき$y=-3$である。
このとき、$y$を$x$の式で表せ。
⑤次の比例式で、$x$の値を求めよ。
$x:(4x-1)=1:x$
⑥$\sqrt{7}$より大きく$\sqrt{31}$より小さい整数をすべて書け。
⑦3つの数$a$、$b$、$c$について、$ab \lt 0$、$abc \gt 0$のとき、$a$、$b$、$c$の符号の組み合わせとして、
最も適当なものを下のア~エの中から1つ選び、記号で答えよ。
※図は動画参照
⑧次のように、1から6までの数字がくり返し並んでいる。
左から100番目の数字は何か。
1、2、3、4、5、6、1、2、3、4、5、6、1、2・・・
⑨右の図のように、$AB=AC$である。
二等辺三角形$ABC$と、頂点$A$、$C$をそれぞれ通る2本の平行な直線$l$、$m$がある。
このときの$\angle x$大きさは何度か。
この動画を見る
高校受験対策・死守71
①$8÷4+6$を計算せよ。
②$\frac{1}{2}+\frac{9}{10}×\frac{5}{3}$を計算せよ。
④$y$は$x$に反比例し、$x=2$のとき$y=-3$である。
このとき、$y$を$x$の式で表せ。
⑤次の比例式で、$x$の値を求めよ。
$x:(4x-1)=1:x$
⑥$\sqrt{7}$より大きく$\sqrt{31}$より小さい整数をすべて書け。
⑦3つの数$a$、$b$、$c$について、$ab \lt 0$、$abc \gt 0$のとき、$a$、$b$、$c$の符号の組み合わせとして、
最も適当なものを下のア~エの中から1つ選び、記号で答えよ。
※図は動画参照
⑧次のように、1から6までの数字がくり返し並んでいる。
左から100番目の数字は何か。
1、2、3、4、5、6、1、2、3、4、5、6、1、2・・・
⑨右の図のように、$AB=AC$である。
二等辺三角形$ABC$と、頂点$A$、$C$をそれぞれ通る2本の平行な直線$l$、$m$がある。
このときの$\angle x$大きさは何度か。
【一度は解きたい!三角形と円を見つめる5分間】図形:法政大学第二高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#中3数学#円#平面図形#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 法政大学第二高等学校
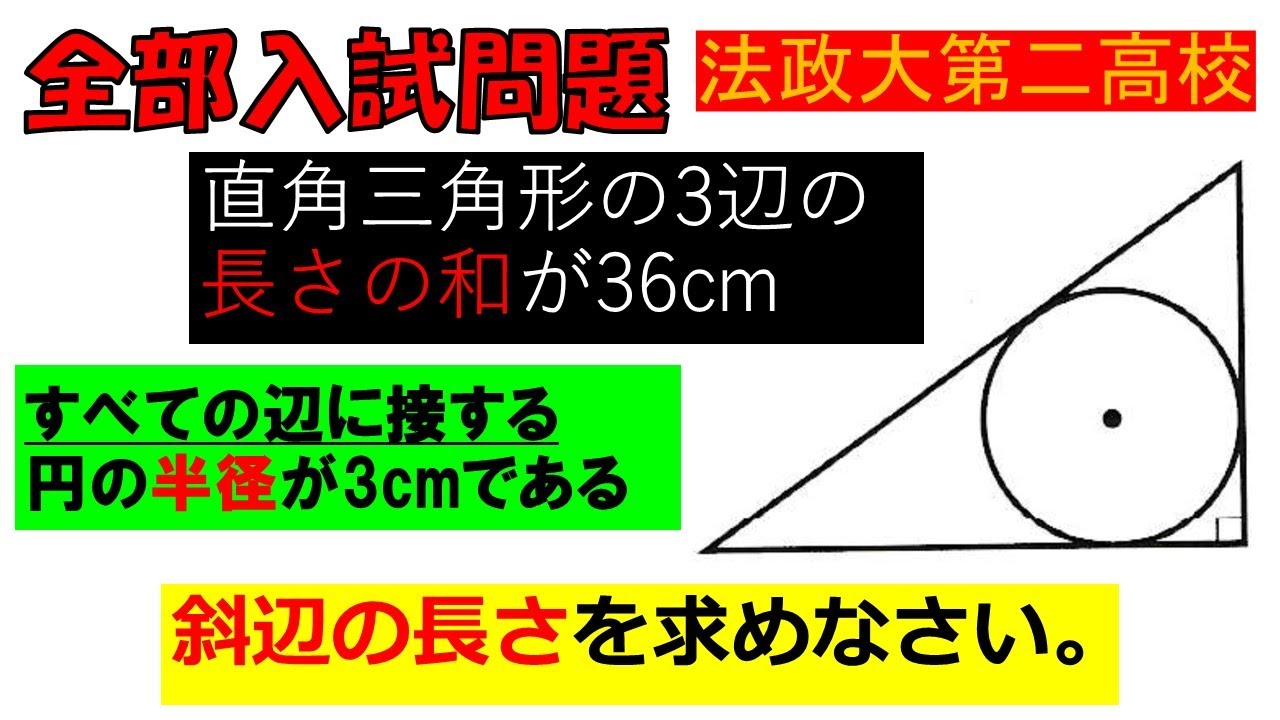
直角三角形の3辺の長さの和が36cm
すべての辺に接する円の半径が3cmである
斜辺の長さを求めなさい。
※図は動画内参照
この動画を見る
入試問題 法政大学第二高等学校
直角三角形の3辺の長さの和が36cm
すべての辺に接する円の半径が3cmである
斜辺の長さを求めなさい。
※図は動画内参照
【まずは3分!先を見通せる力!】図形:専修大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#中3数学#円#平面図形#高校入試過去問(数学)#専修大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 専修大学附属高等学校
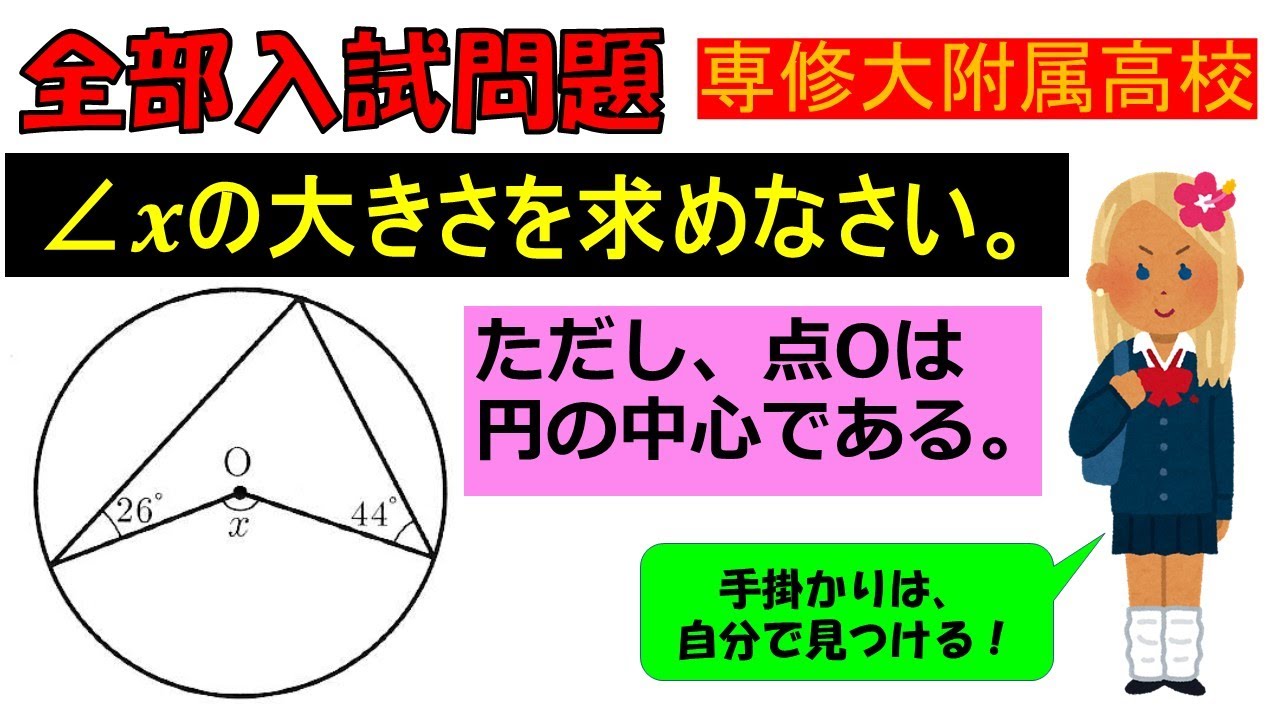
$\angle x$ の大きさを求めなさい。
ただし、点Oは 円の中心である。
※図は動画内参照
この動画を見る
入試問題 専修大学附属高等学校
$\angle x$ の大きさを求めなさい。
ただし、点Oは 円の中心である。
※図は動画内参照
【3分で別解まで分かる!】図形:長崎県~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)#長崎県公立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 長崎県の公立高校
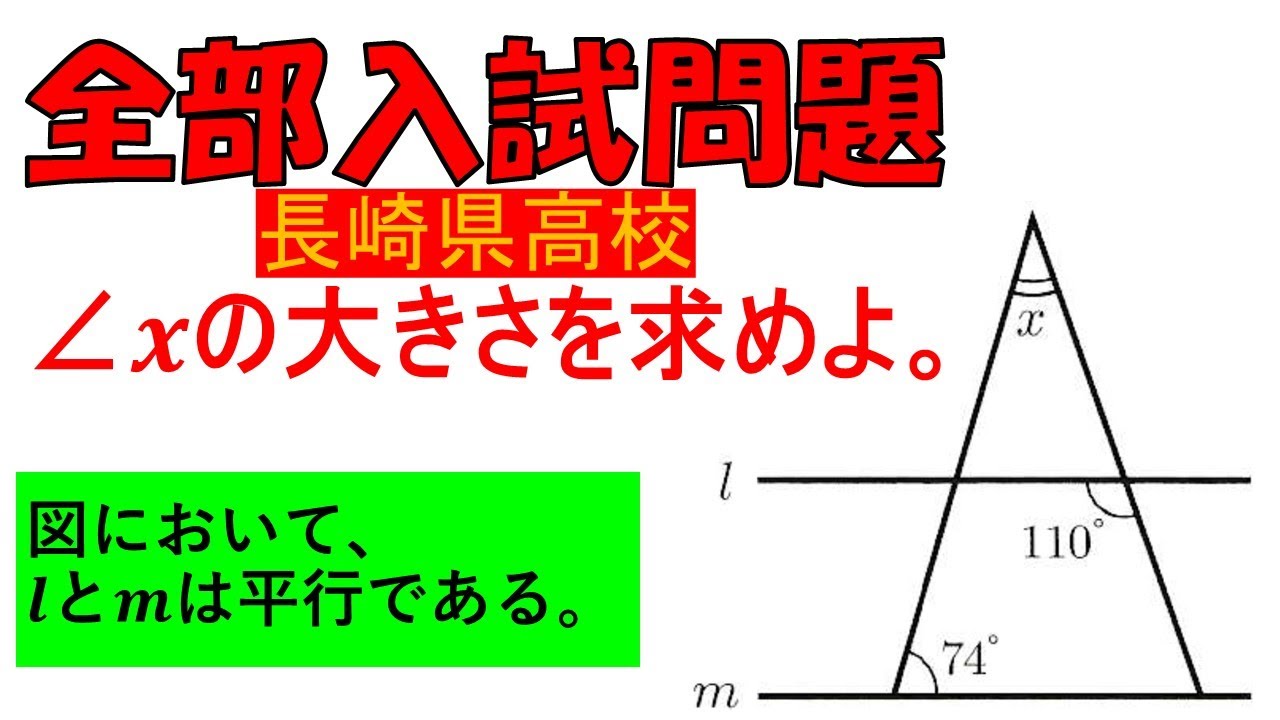
$\angle x$の大きさを求めよ。
図において、$l$と$m$は平行である。
※図は動画内参照
この動画を見る
入試問題 長崎県の公立高校
$\angle x$の大きさを求めよ。
図において、$l$と$m$は平行である。
※図は動画内参照
【中学数学】座標上の四角形の面積の裏技~一瞬で求めよう~【中1数学】

【3分で数学の知識が1 up!】図形:佐賀県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#空間図形#平面図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 佐賀県の公立高校
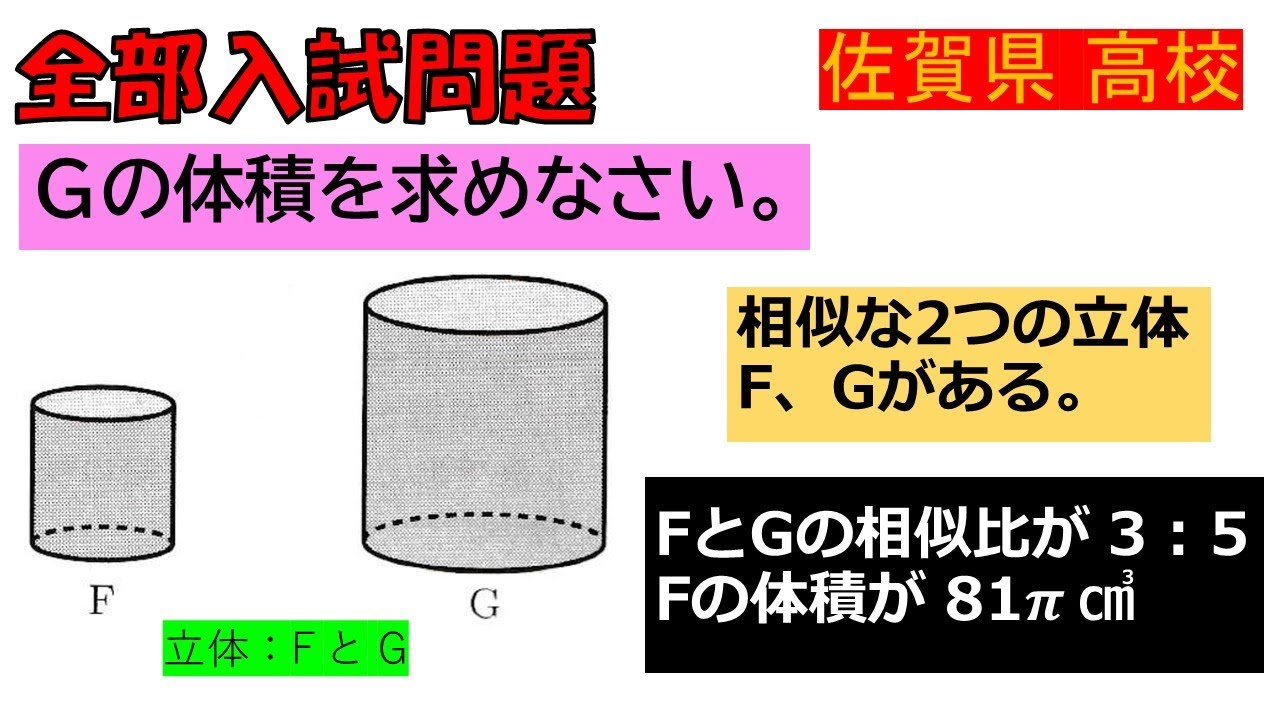
$G$の体積を求めなさい。
相似な2つの立体 $F$、$G$がある。
$F$と$G$の相似比が$3:5$
Fの体積が $81πcm^3$
※図は動画内参照
この動画を見る
入試問題 佐賀県の公立高校
$G$の体積を求めなさい。
相似な2つの立体 $F$、$G$がある。
$F$と$G$の相似比が$3:5$
Fの体積が $81πcm^3$
※図は動画内参照
この面積求めよ~対角線が垂直に交わる四角形の面積の求め方~

単元:
#算数(中学受験)#数学(中学生)#中1数学#平面図形#平面図形#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
対角線が垂直に交わる四角形の面積の求め方
この動画を見る
対角線が垂直に交わる四角形の面積の求め方
高校入試 図形 明大中野
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
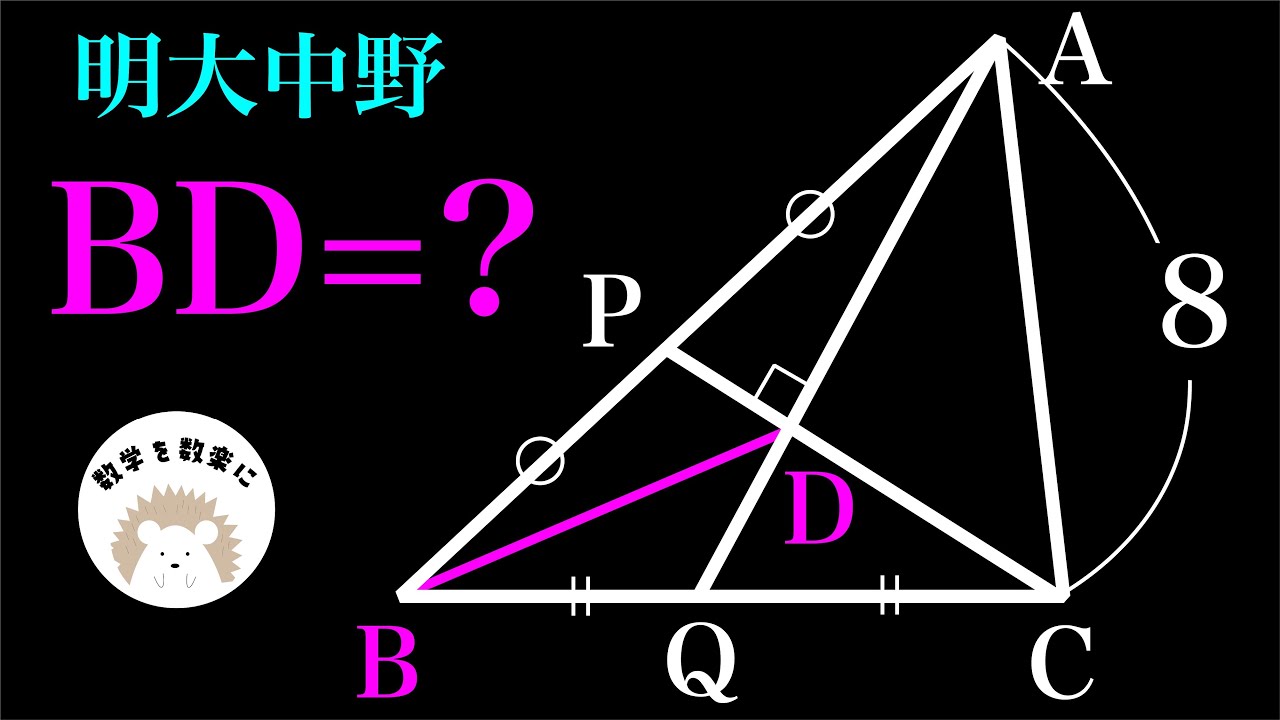
BD=?
*図は動画内参照
明治大学付属中野高等学校
この動画を見る
BD=?
*図は動画内参照
明治大学付属中野高等学校
【図形の見方が変わる!】図形:明治学院高等学校~全国入試問題解法
単元:
#数学(中学生)#平面図形#高校入試過去問(数学)#明治学院高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治学院高等学校
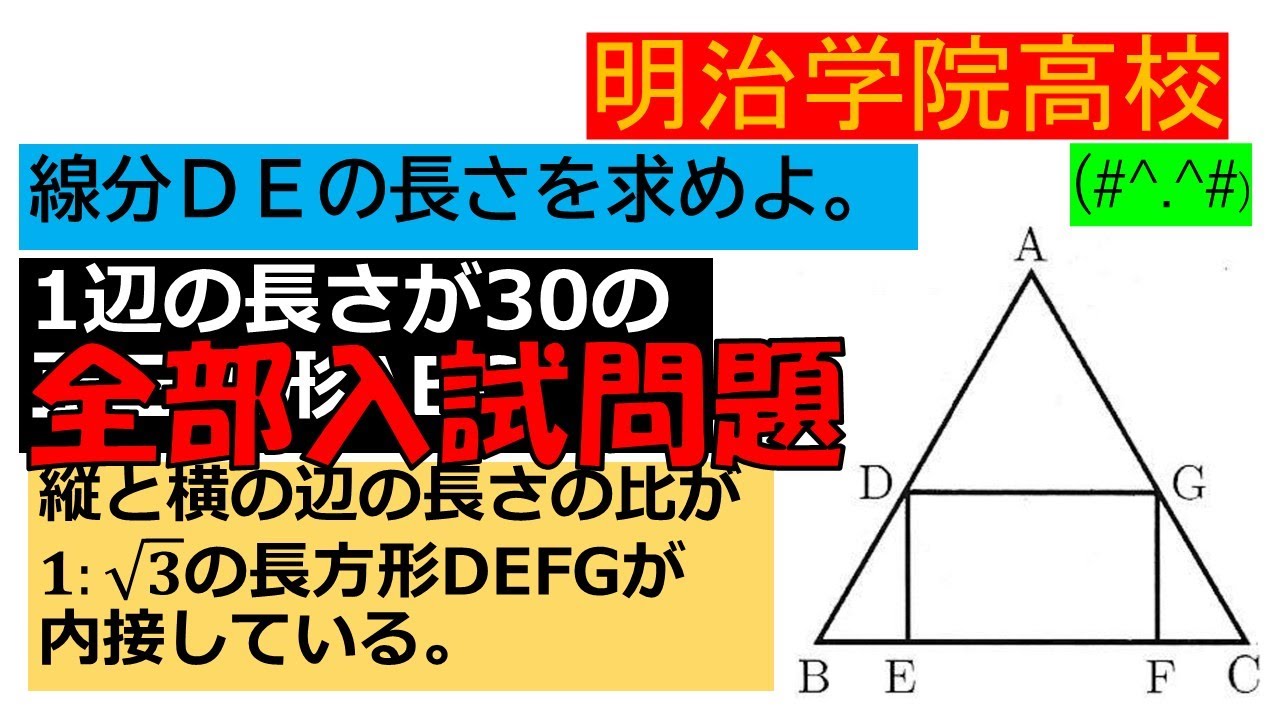
線分$DE$の長さを求めよ。
1辺の長さが30の正三角形$ABC$
縦と横の辺の長さの比が
$1:\sqrt{ 3 }$の長方形$DEFG$が
内接している。
※図は動画内参照
この動画を見る
入試問題 明治学院高等学校
線分$DE$の長さを求めよ。
1辺の長さが30の正三角形$ABC$
縦と横の辺の長さの比が
$1:\sqrt{ 3 }$の長方形$DEFG$が
内接している。
※図は動画内参照
解き方が面白い図形の角度の問題~正方形の中の角度を求めよ~

単元:
#算数(中学受験)#数学(中学生)#中1数学#平面図形#平面図形#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
解き方が面白い図形の角度の問題紹介、解説動画です
この動画を見る
解き方が面白い図形の角度の問題紹介、解説動画です
【中学数学】弧の長さを求めよ~文字式の利用の問題~ 1-6.5【中2数学】

単元:
#算数(中学受験)#数学(中学生)#中1数学#中2数学#平面図形#文字と式#平面図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
動画内の図は線分ABを2つの線分に分け、それぞれの線分を直径として作った円である。
太線は2つの半円の弧をつないだものである。
AB=8cmのとき、太線の長さを求めよ。(円周率は$\pi$を用いよ。)
この動画を見る
動画内の図は線分ABを2つの線分に分け、それぞれの線分を直径として作った円である。
太線は2つの半円の弧をつないだものである。
AB=8cmのとき、太線の長さを求めよ。(円周率は$\pi$を用いよ。)
【5分で得意分野へ!】図形:専修大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#平面図形#高校入試過去問(数学)#専修大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 専修大学附属高等学校
線分$AH$の長さを求めなさい。
$\angle AHB=90°$
三角形$ABC:$
AB=13
BC=14
CA=15
※図は動画内参照
この動画を見る
入試問題 専修大学附属高等学校
線分$AH$の長さを求めなさい。
$\angle AHB=90°$
三角形$ABC:$
AB=13
BC=14
CA=15
※図は動画内参照
高校入試 図形 意外と苦戦するかも 図形
円の面積の公式の面白い証明を2種類紹介します

単元:
#算数(中学受験)#数学(中学生)#中1数学#平面図形#図形の移動#平面図形その他#平面図形#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
円の面積の公式の面白い証明 2種類紹介動画です
この動画を見る
円の面積の公式の面白い証明 2種類紹介動画です
筑駒中 図形問題
単元:
#数学(中学生)#中1数学#平面図形
指導講師:
鈴木貫太郎
問題文全文(内容文):
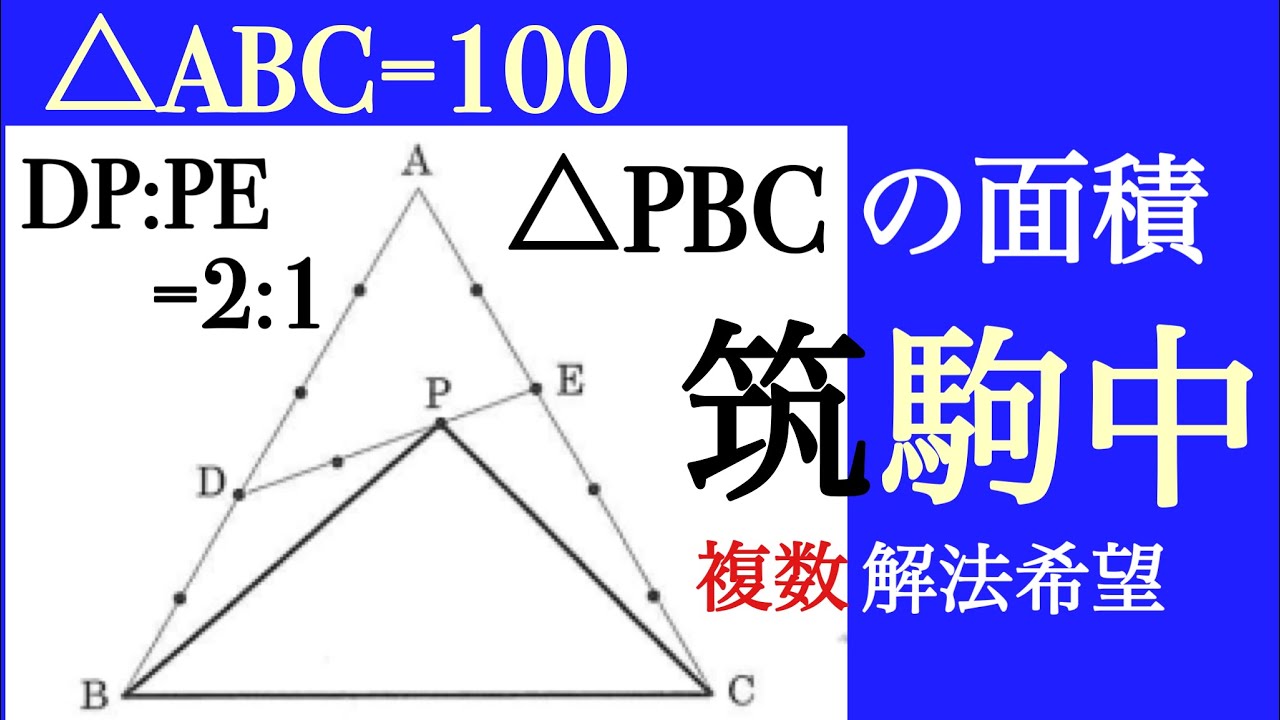
正三角形$ABC$は$100cm^2$である.
$\triangle BCP$の面積を求めよ.
2016筑駒中過去問
この動画を見る
正三角形$ABC$は$100cm^2$である.
$\triangle BCP$の面積を求めよ.
2016筑駒中過去問
【TikTok】扇形の面積を一瞬で求める

中学受験算数 図形

楽々解こう!
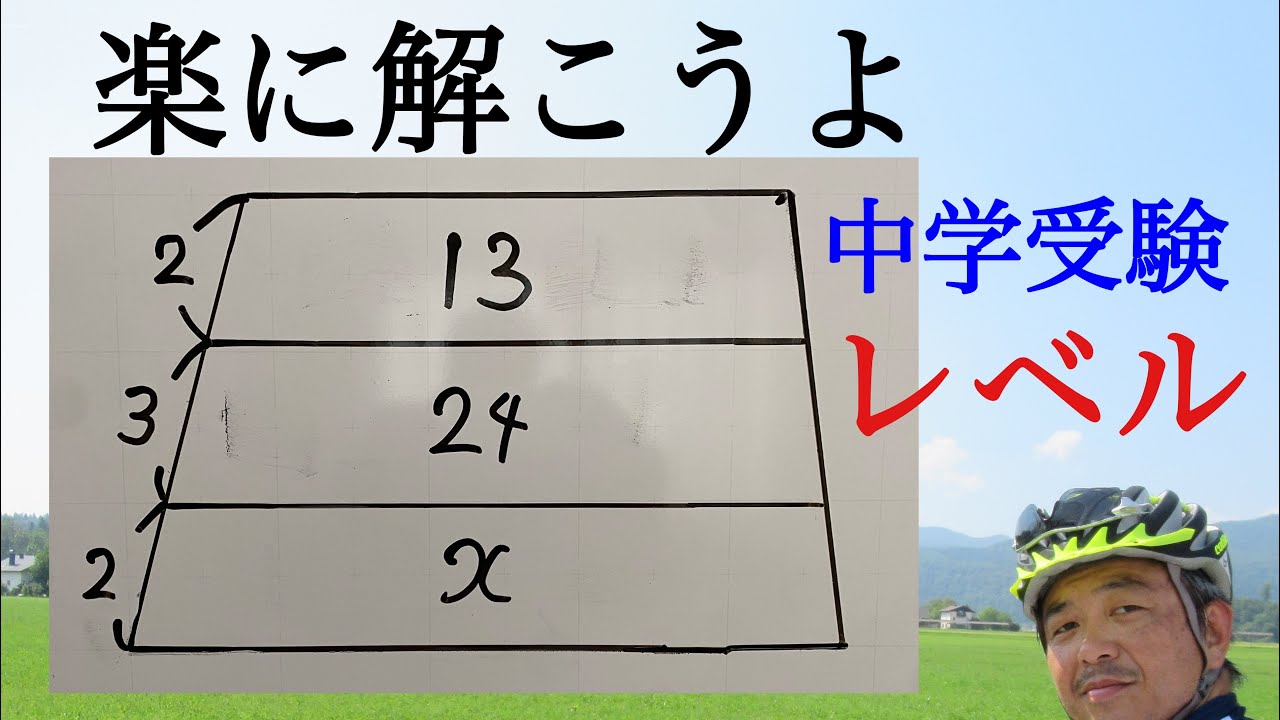
図形問題 中学生範囲

【中学数学・数B】1次関数・平面ベクトル:座標平面上の三角形の面積

単元:
#数学(中学生)#中1数学#中2数学#1次関数#平面図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
2x+y-6=0
2x-y+2=0
2x-7y-22=0
によって作られる三角形の面積は?
この動画を見る
2x+y-6=0
2x-y+2=0
2x-7y-22=0
によって作られる三角形の面積は?
【中学数学】中学数学で球の体積と表面積の公式の証明

【中学数学】作図の演習~鹿児島県公立高校入試2019年~【高校受験】

証明:沖縄県高校入試~全国入試問題解法
単元:
#数学(中学生)#平行と合同#相似な図形#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
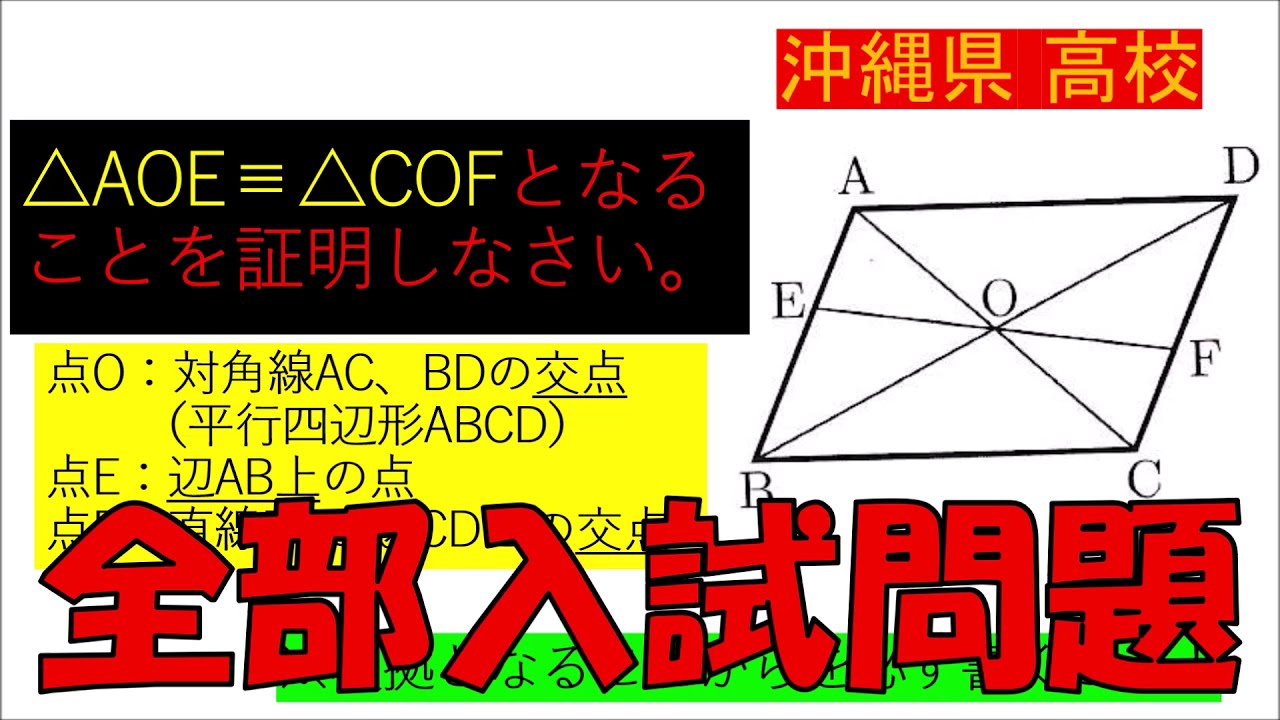
入試問題 沖縄県の高校
$\triangle AOE \equiv \triangle COF$となる
ことを証明しなさい。
点O:対角線$AC$、$BD$の交点 (平行四辺形$ABCD$)
点E:辺$AB$上の点
点F:直線$EO$と辺$CD$との交点
※根拠となることがらを必ず書くこと!
※図は動画内参照
この動画を見る
入試問題 沖縄県の高校
$\triangle AOE \equiv \triangle COF$となる
ことを証明しなさい。
点O:対角線$AC$、$BD$の交点 (平行四辺形$ABCD$)
点E:辺$AB$上の点
点F:直線$EO$と辺$CD$との交点
※根拠となることがらを必ず書くこと!
※図は動画内参照
【中学数学】扇形の中心角の公式~方程式を立てなくても求まる~【中1数学】

平面図形:東京学芸大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)#東京学芸大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
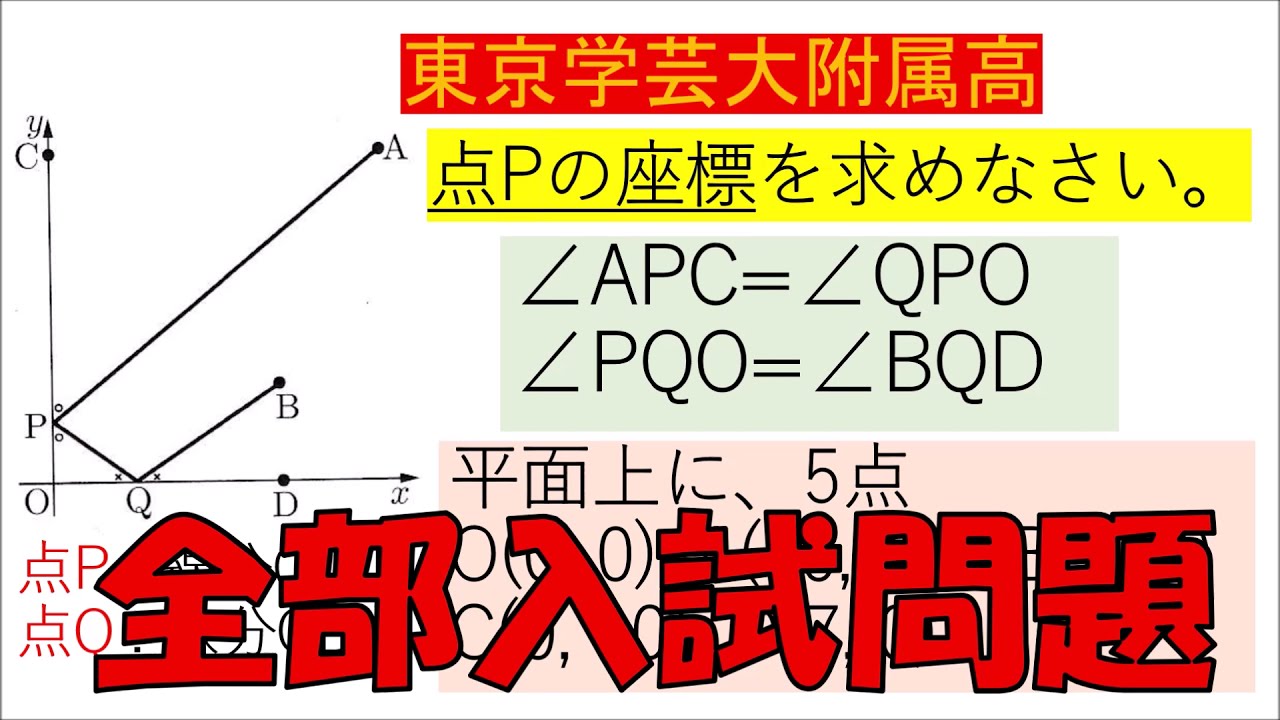
入試問題 東京学芸大学附属高等学校
点$P$の座標を求めなさい。
$\angle APC=\angle QPO$
$\angle PQO=\angle BQD$
平面上に、5点
点$P$:線分$OC$上
点$Q$:線分$OD$上
$O(0, 0), A(10, 10), B(7, 3)$
$C(0, 10), D(7, 0)$
この動画を見る
入試問題 東京学芸大学附属高等学校
点$P$の座標を求めなさい。
$\angle APC=\angle QPO$
$\angle PQO=\angle BQD$
平面上に、5点
点$P$:線分$OC$上
点$Q$:線分$OD$上
$O(0, 0), A(10, 10), B(7, 3)$
$C(0, 10), D(7, 0)$
2021早稲田本庄(改)C 図形
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
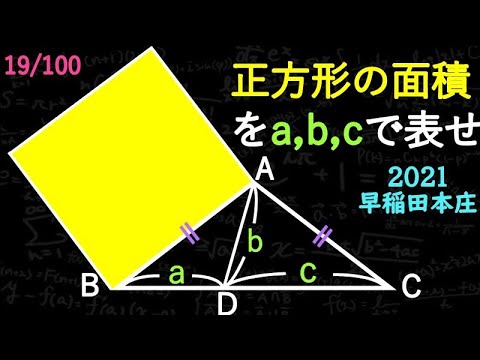
正方形の面積をa,b,cで表せ
*図は動画内参照
2021早稲田大学 本庄高等学院
この動画を見る
正方形の面積をa,b,cで表せ
*図は動画内参照
2021早稲田大学 本庄高等学院
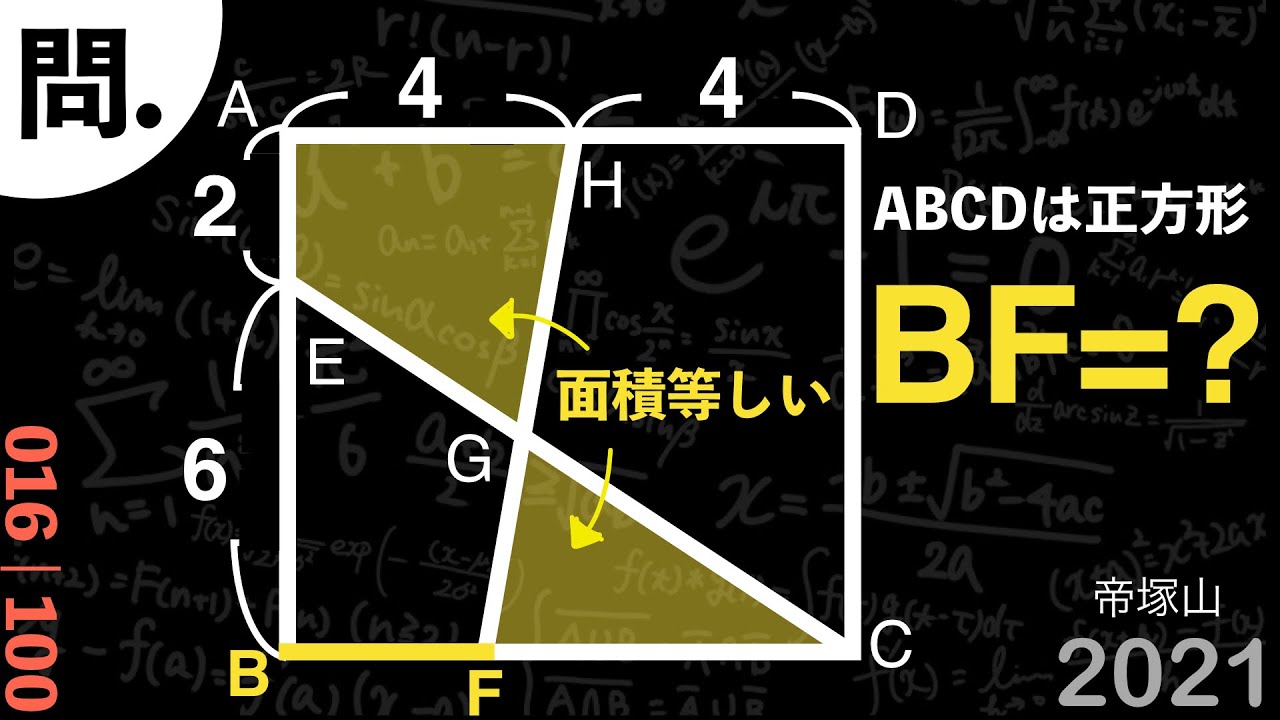
2021 帝塚山 B 図形問題
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形AEGH=△GFC
*図は動画内参照
2021帝塚山高等学校
この動画を見る
四角形AEGH=△GFC
*図は動画内参照
2021帝塚山高等学校
平面図形 良問! 2021西大和学園 B
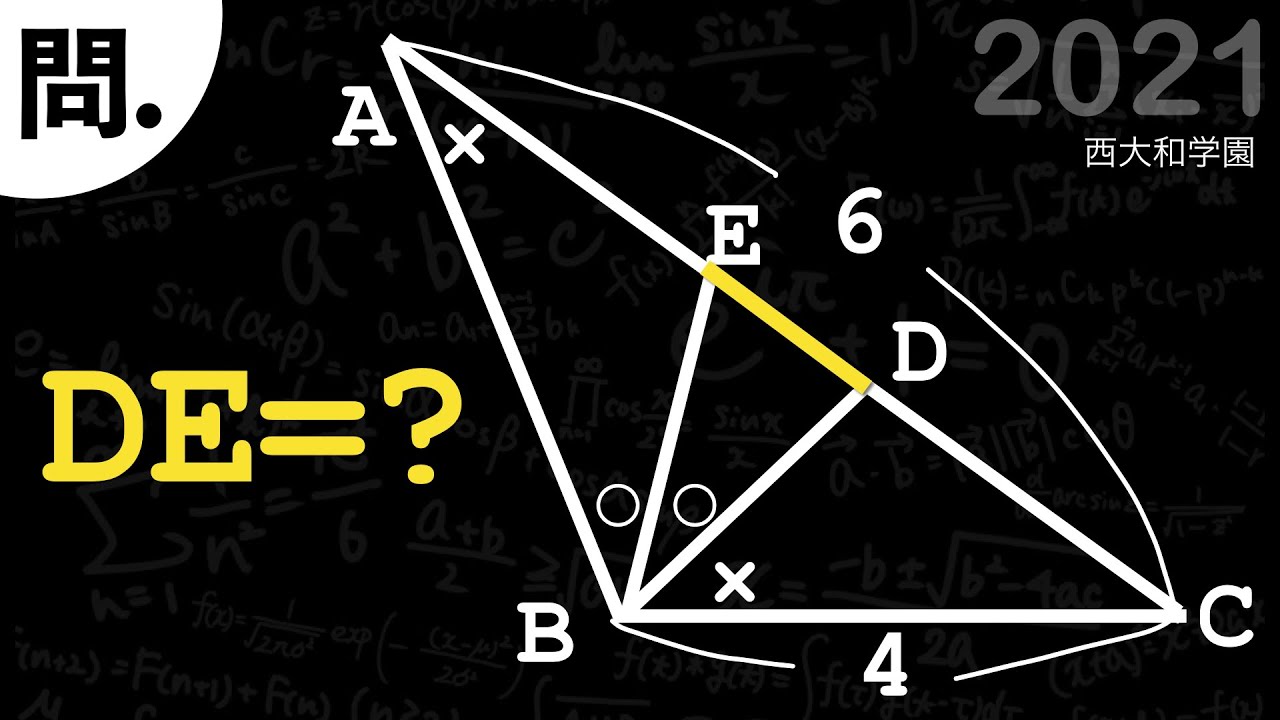
【中学数学】平面図形の演習・証明~岐阜県公立高校入試2018年度~【高校受験】

単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)#受験年度の数字を含む問題
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
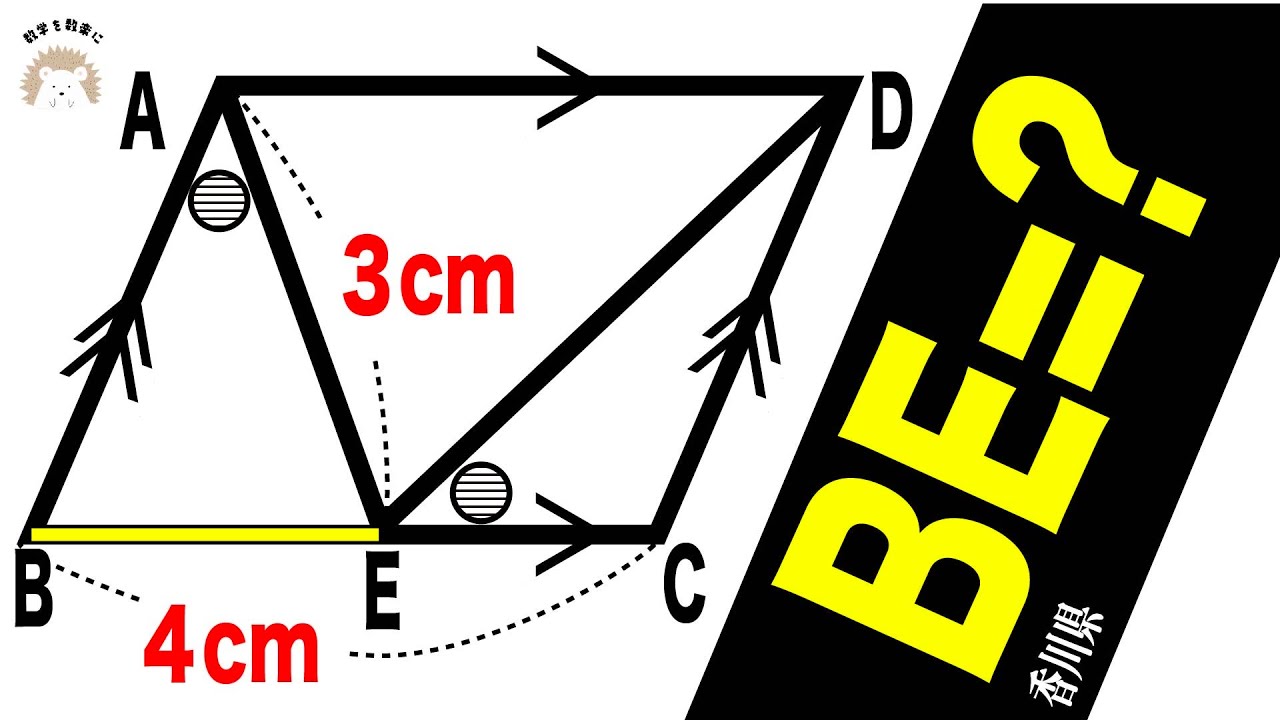
動画内図で、$\triangle BDC$と$\triangle ACE$はともに正三角形である。
また、線分ADとBEとの交点をF,ADと辺BCとの交点をGとする。
(1) $\triangle ADC \equiv EBC$であることを証明せよ。
(2) AB=4cm,AC=4cm,BC=6cmのとき、
(ア) DGの長さを求めよ。
(イ) EFの長さを求めよ。
この動画を見る
動画内図で、$\triangle BDC$と$\triangle ACE$はともに正三角形である。
また、線分ADとBEとの交点をF,ADと辺BCとの交点をGとする。
(1) $\triangle ADC \equiv EBC$であることを証明せよ。
(2) AB=4cm,AC=4cm,BC=6cmのとき、
(ア) DGの長さを求めよ。
(イ) EFの長さを求めよ。
【高校受験対策/数学】死守67

単元:
#数学(中学生)#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#比例・反比例#平行と合同#確率#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守67
① 2次方程式を$x^3+3x-1=0$を解きなさい。
②$\sqrt{24}\div\sqrt{3}-\sqrt{2}$を計算しなさい。
③関数$y=\frac{3}{x}$について、$x$の変域が$1 \leqq x \leqq 6$のとき、$y$の変域を答えなさい。
④
$x$枚の空の封筒と$y$本の鉛筆がある。
封筒の中に鉛筆を4本ずつ入れると8本足りず、3本ずつ入れると12本余る。
このとき$x$と$y$の値を求めなさい。
⑤
右の図のような、$AD=2cm$、$BC=5cm$、$AD/\!/BC$である台形$ABCD$があり、対角線$AC$、$BD$の交点を$E$とする。
点$E$から辺$DC$上に辺$BC$と線分$EF$が平行となる点$F$をとるとき、線分$EF$の長さを答えなさい。
⑥
1から6までの目のついた大、小2つのさいころを同時に投げたとき、大きいさいころの出た目の数を$a$、小さいさいころの出た目の数を$b$とする。
このとき、出た目の数の積$a×b$の値が25以下となる確率を求めなさい。
⑦
右の図のように直線$l$と2つの点$A$、$B$がある。
直線$l$上にあって、2つの点$A$、$B$を通る円の中心$P$を、定規とコンパスを用いて作図しなさい。
ただし作図に使った線は消さずに残しておくこと。
この動画を見る
高校受験対策・死守67
① 2次方程式を$x^3+3x-1=0$を解きなさい。
②$\sqrt{24}\div\sqrt{3}-\sqrt{2}$を計算しなさい。
③関数$y=\frac{3}{x}$について、$x$の変域が$1 \leqq x \leqq 6$のとき、$y$の変域を答えなさい。
④
$x$枚の空の封筒と$y$本の鉛筆がある。
封筒の中に鉛筆を4本ずつ入れると8本足りず、3本ずつ入れると12本余る。
このとき$x$と$y$の値を求めなさい。
⑤
右の図のような、$AD=2cm$、$BC=5cm$、$AD/\!/BC$である台形$ABCD$があり、対角線$AC$、$BD$の交点を$E$とする。
点$E$から辺$DC$上に辺$BC$と線分$EF$が平行となる点$F$をとるとき、線分$EF$の長さを答えなさい。
⑥
1から6までの目のついた大、小2つのさいころを同時に投げたとき、大きいさいころの出た目の数を$a$、小さいさいころの出た目の数を$b$とする。
このとき、出た目の数の積$a×b$の値が25以下となる確率を求めなさい。
⑦
右の図のように直線$l$と2つの点$A$、$B$がある。
直線$l$上にあって、2つの点$A$、$B$を通る円の中心$P$を、定規とコンパスを用いて作図しなさい。
ただし作図に使った線は消さずに残しておくこと。
