 連立方程式
連立方程式
 連立方程式
連立方程式
【ケントウする点は…!】連立方程式:大阪星光学院高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x,y $の連立方程式であり,$ a,b $は正の数である.
$\begin{eqnarray}
\left\{
\begin{array}{l}
ax-y=4 \\
x+by=7
\end{array}
\right.
\end{eqnarray}$
の解を$ a $と$ b $を用いて表すと$ x=\Box,y=\Box $である.
大阪星光学院高校過去問
$ x,y $の連立方程式であり,$ a,b $は正の数である.
この動画を見る
$ x,y $の連立方程式であり,$ a,b $は正の数である.
$\begin{eqnarray}
\left\{
\begin{array}{l}
ax-y=4 \\
x+by=7
\end{array}
\right.
\end{eqnarray}$
の解を$ a $と$ b $を用いて表すと$ x=\Box,y=\Box $である.
大阪星光学院高校過去問
$ x,y $の連立方程式であり,$ a,b $は正の数である.
【解への道筋は…!】連立方程式:お茶の水女子大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x-\dfrac{a+5}{2}y=-2 \\
2ax+15y=1
\end{array}
\right.
\end{eqnarray}$
$ y=\dfrac{1}{3}$のとき,定数$ a $の値として考えられるものをすべて求めなさい.
お茶の水女子大学附属高等学校過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x-\dfrac{a+5}{2}y=-2 \\
2ax+15y=1
\end{array}
\right.
\end{eqnarray}$
$ y=\dfrac{1}{3}$のとき,定数$ a $の値として考えられるものをすべて求めなさい.
お茶の水女子大学附属高等学校過去問
二乗を含む連立方程式 本郷高校
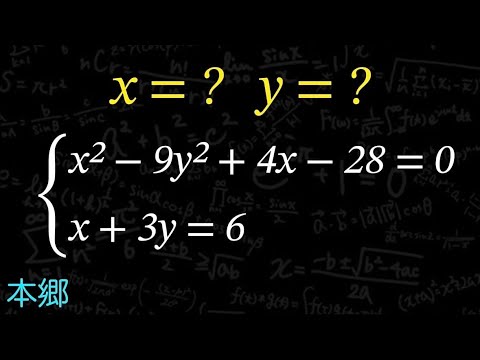
単元:
#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
$x=?$ $\quad$ $y=?$
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 - 9y^2 + 4x -28 = 0 \\
x + 3y = 6
\end{array}
\right.
\end{eqnarray}
本郷高等学校
この動画を見る
$x=?$ $\quad$ $y=?$
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 - 9y^2 + 4x -28 = 0 \\
x + 3y = 6
\end{array}
\right.
\end{eqnarray}
本郷高等学校
気付けば一瞬な連立方程式

単元:
#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y +2z= 2 \\
x + 2y +z= 7 \\
2x + y + z = -1
\end{array}
\right.
\end{eqnarray}
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y +2z= 2 \\
x + 2y +z= 7 \\
2x + y + z = -1
\end{array}
\right.
\end{eqnarray}
【自力で解きたい!】連立方程式:渋谷教育学園幕張高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
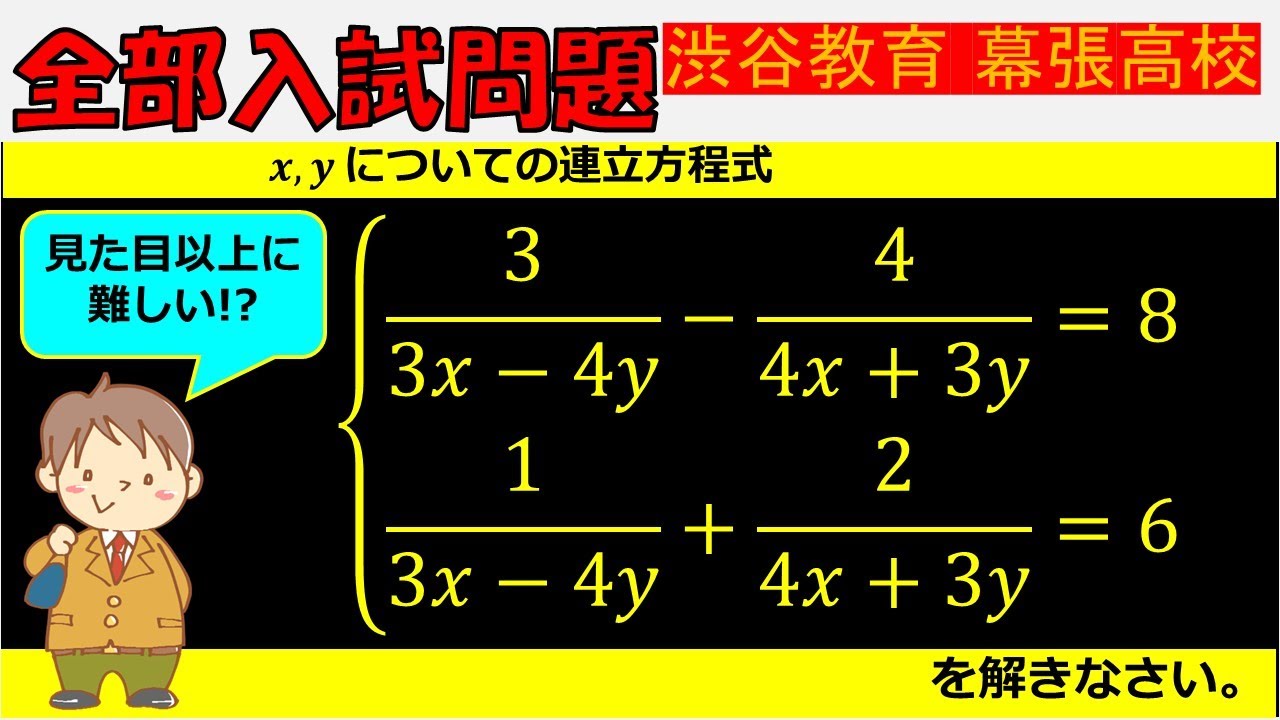
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{3x-4y}-\dfrac{4}{4x+3y}=8 \\
\dfrac{1}{3x-4y}+\dfrac{2}{4x+3y}=6
\end{array}
\right.
\end{eqnarray}$
を解きなさい.
渋谷教育幕張高校過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{3x-4y}-\dfrac{4}{4x+3y}=8 \\
\dfrac{1}{3x-4y}+\dfrac{2}{4x+3y}=6
\end{array}
\right.
\end{eqnarray}$
を解きなさい.
渋谷教育幕張高校過去問
【本当に解はあるのか!?】整数:日本大学習志野高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#高校入試過去問(数学)#日本大学習志野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
3つの自然数$ x,y,z(x \lt y \lt z)$である.
$ x+y+z=20 $
$ xyz=60 $ 満たす.
このとき, $ x=\Box,y=\Box,z=\Box $
日大習志野高校過去問
この動画を見る
3つの自然数$ x,y,z(x \lt y \lt z)$である.
$ x+y+z=20 $
$ xyz=60 $ 満たす.
このとき, $ x=\Box,y=\Box,z=\Box $
日大習志野高校過去問
【中学数学】数学用語チェック絵本 中2の用語”せめて”これだけは覚えよう!!act2まとめ

単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#資料の活用#1次関数#平行と合同#確率#三角形と四角形
指導講師:
理数個別チャンネル
問題文全文(内容文):
中2で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!act2vol.1~7の方も見てね♪
この動画を見る
中2で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!act2vol.1~7の方も見てね♪
【未知なるものは…!】文章題:明治学院高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#明治学院高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
所持金で$ \color{red}{プリンを8個}$買うと$ \color{red}{220円}$余り,$ \color{red}{10個}$買うと合計金額から$ \color{blue}{1割引き}$になるので$ \color{red}{60円}$余る.
このときの$ \color{red}{所持金}$はいくらか?
明治学院高校過去問
この動画を見る
所持金で$ \color{red}{プリンを8個}$買うと$ \color{red}{220円}$余り,$ \color{red}{10個}$買うと合計金額から$ \color{blue}{1割引き}$になるので$ \color{red}{60円}$余る.
このときの$ \color{red}{所持金}$はいくらか?
明治学院高校過去問
気付けば気持ちいい!!連立方程式 慶應義塾

単元:
#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 6 \\
6xy = 5
\end{array}
\right.
\end{eqnarray}
慶應義塾高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 6 \\
6xy = 5
\end{array}
\right.
\end{eqnarray}
慶應義塾高等学校
【挑戦しよう!】連立方程式:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x \gt y $において,
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y+xy^2-9xy=120 \\
xy+x+y-9=-22
\end{array}
\right.
\end{eqnarray}$
の解は$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\Box \\
y=\Box
\end{array}
\right.
\end{eqnarray}$ または,$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\Box \\
y=\Box
\end{array}
\right.
\end{eqnarray}$
慶應義塾高校過去問
この動画を見る
$ x \gt y $において,
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y+xy^2-9xy=120 \\
xy+x+y-9=-22
\end{array}
\right.
\end{eqnarray}$
の解は$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\Box \\
y=\Box
\end{array}
\right.
\end{eqnarray}$ または,$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\Box \\
y=\Box
\end{array}
\right.
\end{eqnarray}$
慶應義塾高校過去問
これも連立方程式だって分かってる!?~全国入試問題解法 #shorts #数学 #math #高校受験
単元:
#数学(中学生)#中2数学#中3数学#連立方程式#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
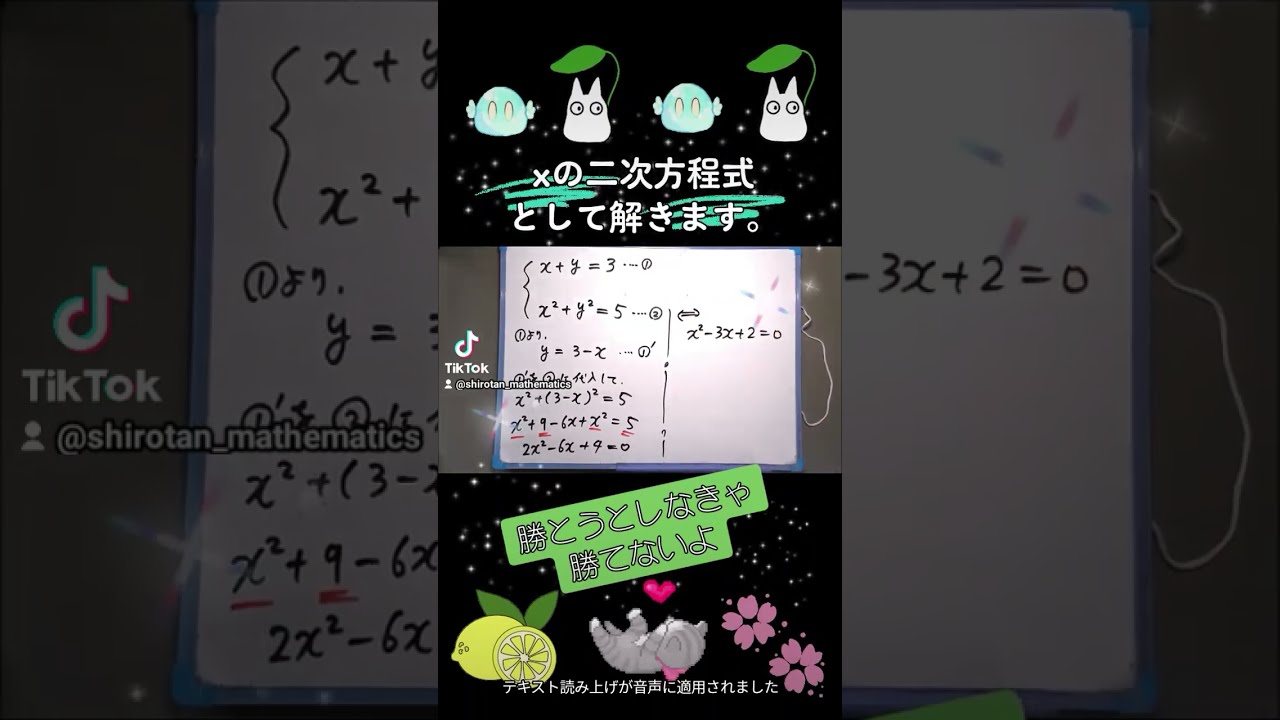
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x + y = 3 \\
x^2+y^2=5
\end{array}
\right.
\end{eqnarray}$ を解け.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x + y = 3 \\
x^2+y^2=5
\end{array}
\right.
\end{eqnarray}$ を解け.
連立方程式にも上手い解き方はある15秒~全国入試問題解法 #shorts #数学 #入試対策 #math #動体視力

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連立方程式にも上手い解き方はある15秒~全国入試問題解法 #shorts #数学 #入試対策 #math #動体視力
この動画を見る
連立方程式にも上手い解き方はある15秒~全国入試問題解法 #shorts #数学 #入試対策 #math #動体視力
手強いぞ 連立方程式 慶應義塾(神奈川)

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け(x>y)
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y + xy^2 -9xy = 120 \\
xy + x + y - 9 = -22
\end{array}
\right.
\end{eqnarray}
2023慶應義塾高等学校(改)
この動画を見る
連立方程式を解け(x>y)
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y + xy^2 -9xy = 120 \\
xy + x + y - 9 = -22
\end{array}
\right.
\end{eqnarray}
2023慶應義塾高等学校(改)
【まずは解くこと…!】文字式:明治大学付属明治高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#平方根#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\sqrt2x+\sqrt7y=3 \\
\sqrt7x-\sqrt2y=-6
\end{array}
\right.
\end{eqnarray}$
のとき,$ y-x=\Box $
明治大学付属明治高等学校過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\sqrt2x+\sqrt7y=3 \\
\sqrt7x-\sqrt2y=-6
\end{array}
\right.
\end{eqnarray}$
のとき,$ y-x=\Box $
明治大学付属明治高等学校過去問
連立方程式
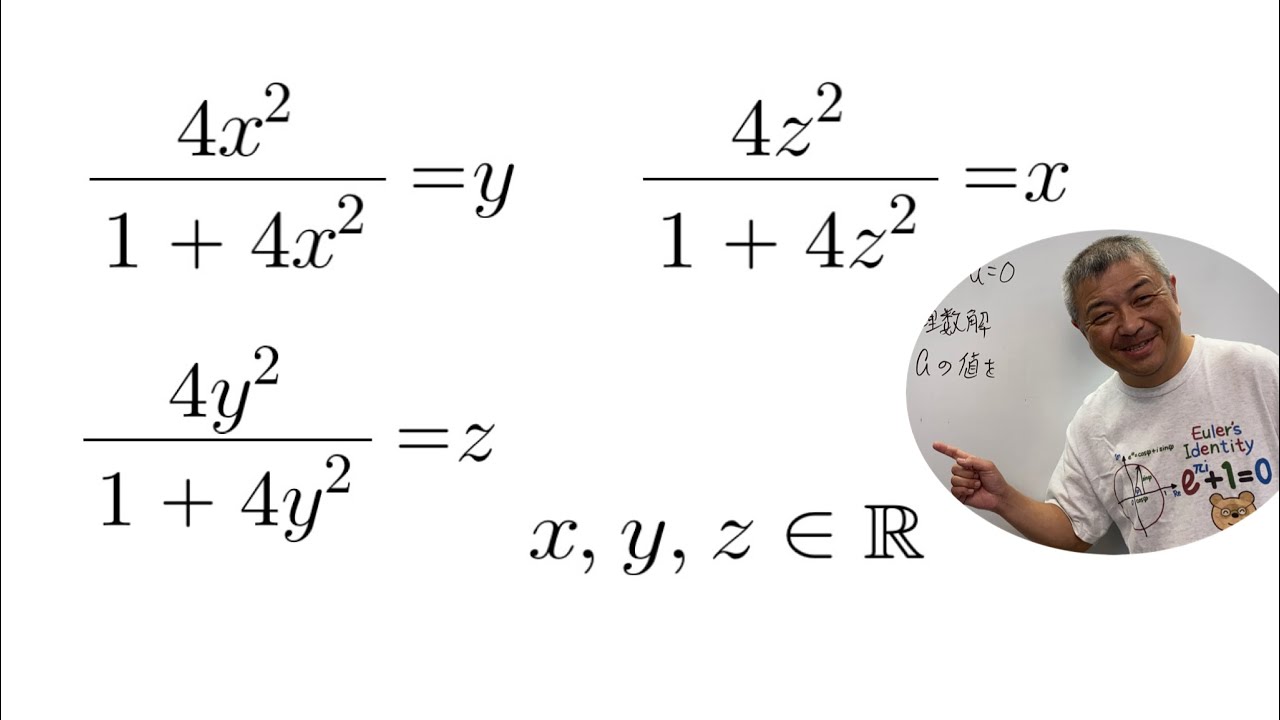
単元:
#連立方程式#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z$は実数とする.これを解け.
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy+x+y=1 \\
x^2y^2+x^2+y^2=31
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$x,y,z$は実数とする.これを解け.
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy+x+y=1 \\
x^2y^2+x^2+y^2=31
\end{array}
\right.
\end{eqnarray}$
【道具を使いこなせ!】連立方程式:東京都公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#東京都公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+3y=1 \\
8x+9y=7
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け.
東京都公立高等学校過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+3y=1 \\
8x+9y=7
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け.
東京都公立高等学校過去問
中学2年生問題 ただの連立方程式

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
2021x+2022y=2023 \\
4045x+4043y=4046
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2021x+2022y=2023 \\
4045x+4043y=4046
\end{array}
\right.
\end{eqnarray}$
これを解け.
解けるように作られた連立方程式

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数$x,y,z$を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+2y+3z)^2=14(x^2+y^2+z^2) \\
x+y+z=18
\end{array}
\right.
\end{eqnarray}$
この動画を見る
実数$x,y,z$を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+2y+3z)^2=14(x^2+y^2+z^2) \\
x+y+z=18
\end{array}
\right.
\end{eqnarray}$
【比の計算ならば…!】連立方程式:広島大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#広島大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x:(2y+13)=3:1\\
5x+6y=3
\end{array}
\right.
\end{eqnarray}$
広大附属高校過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x:(2y+13)=3:1\\
5x+6y=3
\end{array}
\right.
\end{eqnarray}$
広大附属高校過去問
文字3つ 式3つの連立方程式 開成高校

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y + z = \frac{1}{6} \\
2x + y - z = - \frac{1}{2} \\
x + 3y +2z = \frac{1}{6}
\end{array}
\right.
\end{eqnarray}
開成高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x + y + z = \frac{1}{6} \\
2x + y - z = - \frac{1}{2} \\
x + 3y +2z = \frac{1}{6}
\end{array}
\right.
\end{eqnarray}
開成高等学校
ただの連立方程式だよね
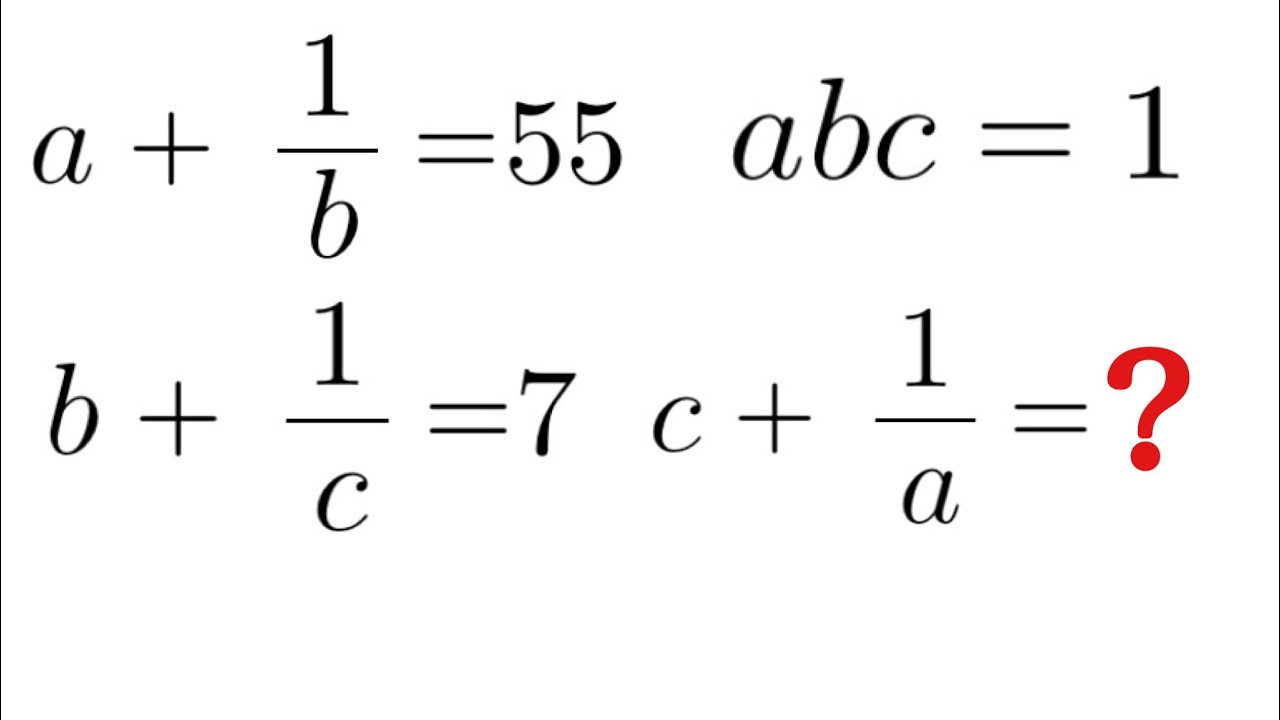
単元:
#数学(中学生)#中2数学#連立方程式#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$abc=1$
$a+\frac{1}{b}=55$
$b+\frac{1}{c}=7$
$C+\frac{1}{a}=?$
この動画を見る
$abc=1$
$a+\frac{1}{b}=55$
$b+\frac{1}{c}=7$
$C+\frac{1}{a}=?$
【裏技】中高生は見ない方がいいかも...

【保存版】連立方程式の考え方

単元:
#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
連立方程式の基本的な考え方
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+y=8・・・① \\
x-y=1・・・②
\end{array}
\right.
\end{eqnarray}$
この動画を見る
連立方程式の基本的な考え方
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+y=8・・・① \\
x-y=1・・・②
\end{array}
\right.
\end{eqnarray}$
連立方程式を上手く解く!~全国入試問題解法 #数学 #shorts #sound #高校入試

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
1001x+999y=1007 \\
999x+1001y=993
\end{array}
\right.
\end{eqnarray}$
東工大科技高校過去問
この動画を見る
次の連立方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
1001x+999y=1007 \\
999x+1001y=993
\end{array}
\right.
\end{eqnarray}$
東工大科技高校過去問
連立方程式の難問を誰でも解けるようにする動画~全国入試問題解法 #shorts #数学 #高校入試 #裏ワザ

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{3x+4y}-\dfrac{4}{4x-3y}=10 \\
\dfrac{4}{3x+4y}+\dfrac{3}{4x-3y}=5
\end{array}
\right.
\end{eqnarray}$
を解け.
東大寺学園高校過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\dfrac{3}{3x+4y}-\dfrac{4}{4x-3y}=10 \\
\dfrac{4}{3x+4y}+\dfrac{3}{4x-3y}=5
\end{array}
\right.
\end{eqnarray}$
を解け.
東大寺学園高校過去問
【「学ぶ」は「真似する」ところから】2元2次連立方程式⑤:中学からの連立方程式~全国入試問題解法
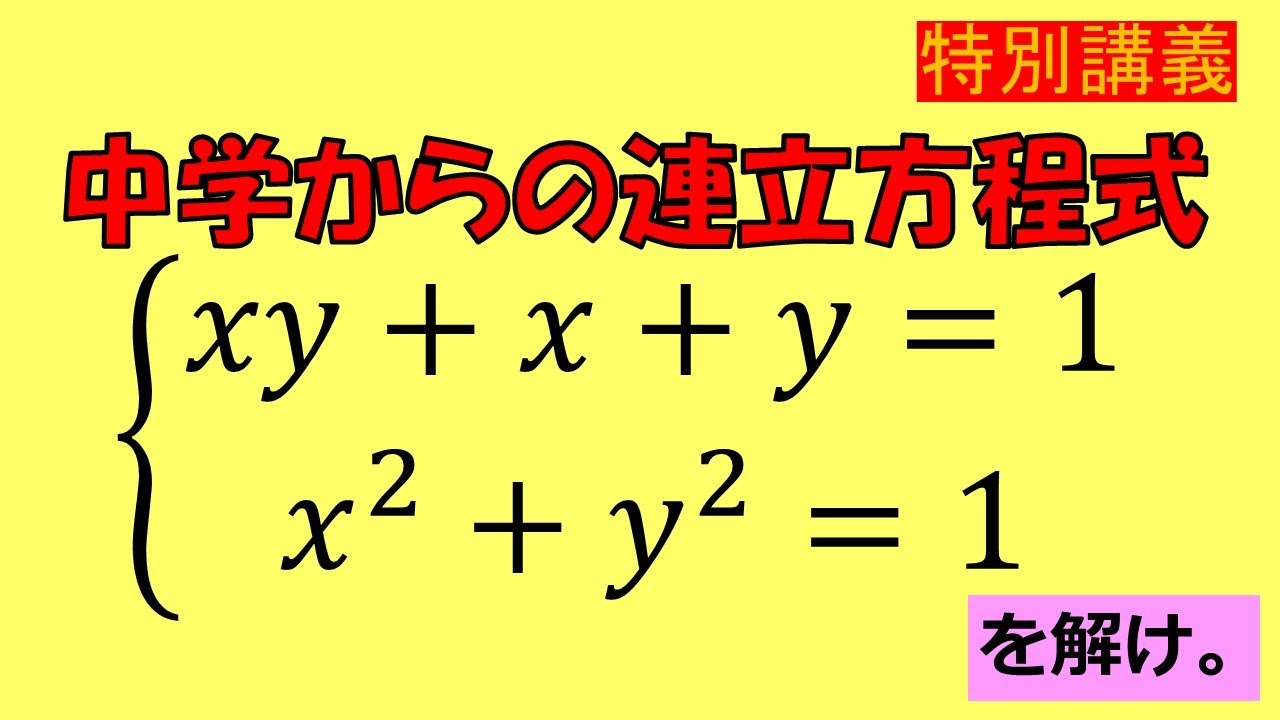
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
xy+x+y=1 \\
x^2+y^2=1
\end{array}
\right.
\end{eqnarray}$
を解け.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
xy+x+y=1 \\
x^2+y^2=1
\end{array}
\right.
\end{eqnarray}$
を解け.
【これまでの知識を利用して】2元2次連立方程式④:中学からの連立方程式~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2+xy-2y^2=4 \\
x^2+2xy-y^2=7
\end{array}
\right.
\end{eqnarray}$
を解け.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2+xy-2y^2=4 \\
x^2+2xy-y^2=7
\end{array}
\right.
\end{eqnarray}$
を解け.
【やり方を短時間でマスター!!】連立方程式(代入法・加減法)〔現役講師解説、中学、数学〕

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
3rd School
問題文全文(内容文):
中学2年生 数学
連立方程式
加減法
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 15 \\
9x - 5y = 12
\end{array}
\right.
\end{eqnarray}$
代入法
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x - 2y = 2 \\
y = x + 2
\end{array}
\right.
\end{eqnarray}$
この動画を見る
中学2年生 数学
連立方程式
加減法
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 15 \\
9x - 5y = 12
\end{array}
\right.
\end{eqnarray}$
代入法
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x - 2y = 2 \\
y = x + 2
\end{array}
\right.
\end{eqnarray}$
【コツをつかめば簡単に解ける!】2元2次連立方程式③:中学からの連立方程式~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
xy+x+2y=6 \\
2xy+x-y=5
\end{array}
\right.
\end{eqnarray}$
を解け.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
xy+x+2y=6 \\
2xy+x-y=5
\end{array}
\right.
\end{eqnarray}$
を解け.
【絶対に「正解」するところから始めよう】2元2次連立方程式②:中学からの連立方程式~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x-y=1 \\
x^2+xy+y^2=7
\end{array}
\right.
\end{eqnarray}$
を解け.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x-y=1 \\
x^2+xy+y^2=7
\end{array}
\right.
\end{eqnarray}$
を解け.
