 連立方程式
連立方程式
 連立方程式
連立方程式
【中学数学】連立方程式:基礎の基礎から解説!その3 表で考えよう

【理解深まる3分間】連立方程式:青森県高等学校~全国入試問題解法【トライ式】

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)#青森県公立高等学校#青森県高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 青森県の高等学校
グラフを利用して解を求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y = x+6 \\
x + 2y = 6
\end{array}
\right.
\end{eqnarray}$
この動画を見る
入試問題 青森県の高等学校
グラフを利用して解を求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y = x+6 \\
x + 2y = 6
\end{array}
\right.
\end{eqnarray}$
連立方程式:東京都立国立高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#東京都立国立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立国立高等学校
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{4x+y-5}{2}=x+0.25y-2 \\
4x + 3y = -6
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
この動画を見る
入試問題 東京都立国立高等学校
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{4x+y-5}{2}=x+0.25y-2 \\
4x + 3y = -6
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
【中学数学】連立方程式:基礎の基礎から解説!その2 元と次って何?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
理数個別チャンネル
問題文全文(内容文):
x-y=6は何元何次方程式でしょうか?意外ときちんと習わない”元”について解説します!
この動画を見る
x-y=6は何元何次方程式でしょうか?意外ときちんと習わない”元”について解説します!
【中学数学】連立方程式:基礎の基礎から解説!その1 連立方程式って?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x+y=10,x-y=6$を同時に満たす整数解を考えながら連立方程式を学んでいこう。
この動画を見る
$x+y=10,x-y=6$を同時に満たす整数解を考えながら連立方程式を学んでいこう。
連立方程式:豊島岡女子学園高等学校~全国入試問題解法【神授業】
単元:
#数学(中学生)#中1数学#中2数学#方程式#連立方程式#高校入試過去問(数学)#豊島岡女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
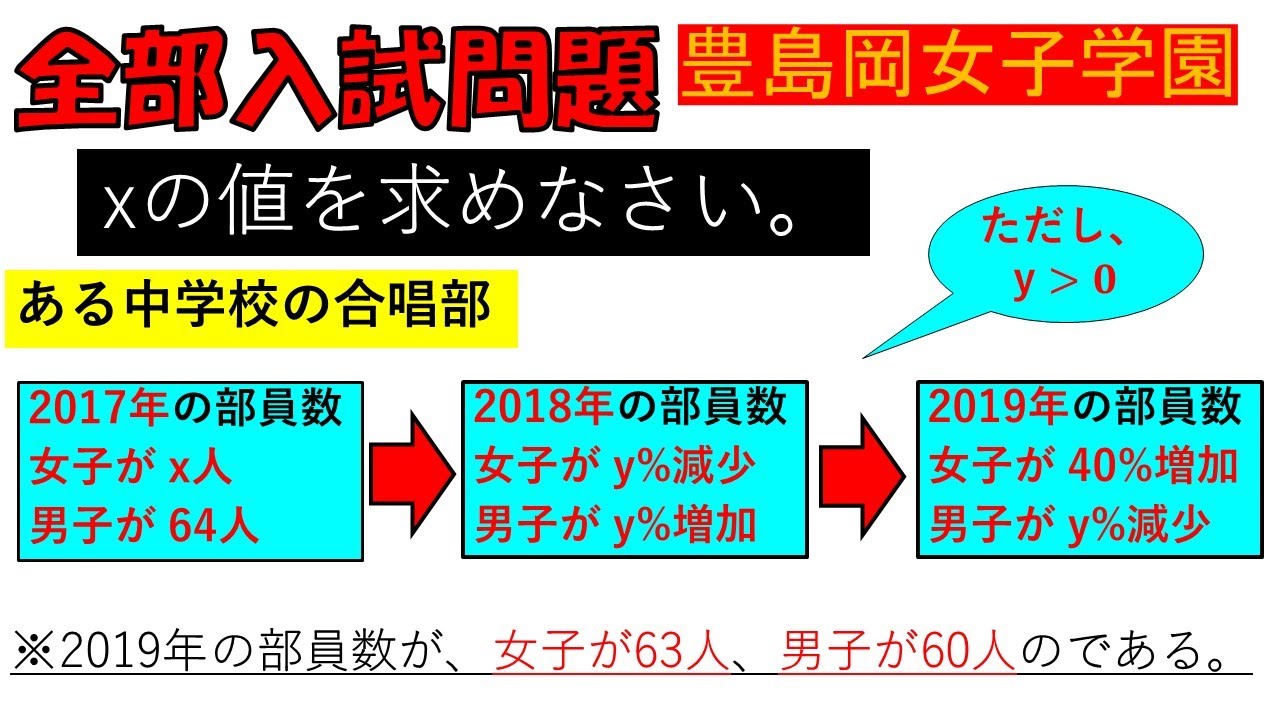
入試問題 豊島岡女子学園高等学校
ある中学校の合唱部の2017年の部員数は、女子が$x$ 人、男子が64人でした。2018年の部員数は、2017 年と比べて女子が$y$%減り、男子が$y$%増えました。 2019年の部員数は、2018年と比べて女子が40%増 え、男子が$y$%減りました。
2019年の部員数が、女子が63人、男子が60人のとき
$x$の値を求めなさい。
(ただし、$ y\gt 0$)
この動画を見る
入試問題 豊島岡女子学園高等学校
ある中学校の合唱部の2017年の部員数は、女子が$x$ 人、男子が64人でした。2018年の部員数は、2017 年と比べて女子が$y$%減り、男子が$y$%増えました。 2019年の部員数は、2018年と比べて女子が40%増 え、男子が$y$%減りました。
2019年の部員数が、女子が63人、男子が60人のとき
$x$の値を求めなさい。
(ただし、$ y\gt 0$)
京都女子
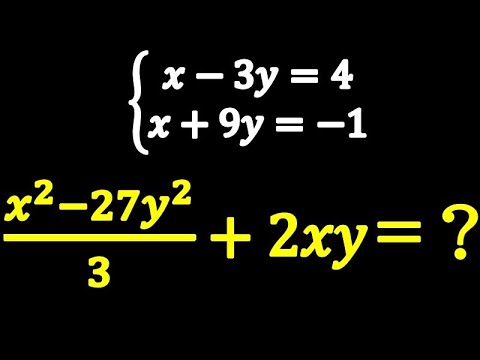
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x - 3y = 4 \\
x + 9y = -1
\end{array}
\right.
\end{eqnarray}
$
のとき
$\frac{x^2-27y^2}{3}+2xy$
京都女子高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x - 3y = 4 \\
x + 9y = -1
\end{array}
\right.
\end{eqnarray}
$
のとき
$\frac{x^2-27y^2}{3}+2xy$
京都女子高等学校
連立方程式:東京都立青山高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#東京都立青山高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立青山高等学校
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{x-1}{3}+\displaystyle \frac{3y+1}{6}= 0 \\
0.4(x+4) + 0.5(y-3) = 0
\end{array}
\right.
\end{eqnarray}$
この動画を見る
入試問題 東京都立青山高等学校
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{x-1}{3}+\displaystyle \frac{3y+1}{6}= 0 \\
0.4(x+4) + 0.5(y-3) = 0
\end{array}
\right.
\end{eqnarray}$
慶應義塾の連立方程式 B

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{5}{x-\sqrt 2}+ \frac{2}{x+\sqrt 2y}=1\\
\frac{1}{x-\sqrt 2}+ \frac{5}{x+\sqrt 2y}=2
\end{array}
\right.
\end{eqnarray}
$
2021慶應義塾高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{5}{x-\sqrt 2}+ \frac{2}{x+\sqrt 2y}=1\\
\frac{1}{x-\sqrt 2}+ \frac{5}{x+\sqrt 2y}=2
\end{array}
\right.
\end{eqnarray}
$
2021慶應義塾高等学校
連立方程式:東京工業大学附属科学技術高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#東京工業大学附属科学技術高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京工業大学附属科学技術高等学校
$x$と$y$の値をそれぞれ求めなさい。
$x:y=3:2$が成り立ち
$x + y = 4$である。
この動画を見る
入試問題 東京工業大学附属科学技術高等学校
$x$と$y$の値をそれぞれ求めなさい。
$x:y=3:2$が成り立ち
$x + y = 4$である。
【高校受験対策/数学】文章題8

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・文章題8
Q.
ある博物館の入館料は、小学生260円、中学生と高校生はともに410円、大人760円である。
ある日の入館者数を調べると、中学生と高校生の合計入館者数は小学生の入館者数の2倍であり、
大人の入館者数は小学生、中学生、高校生の合計入館者数よりも100人少なかった。
この日の小学生の入館者数を$x$人、大人の入館者数を$y$人とするとき、次の問いに答えよ。
①この日の総入館者数を$x$と$y$の両方を用いて表せ。
②さらに、この博物館では1個550円のおみやげを売っており、総入館者数の8割の人が購入した。
この日の総入館者の入館料の合計とおみやげの売上げをあわせた金額は150000円で、おみやげを2個以上買った人はいなかった。
このとき$x$と$y$の値をそれぞれ求めよ。
この動画を見る
高校受験対策・文章題8
Q.
ある博物館の入館料は、小学生260円、中学生と高校生はともに410円、大人760円である。
ある日の入館者数を調べると、中学生と高校生の合計入館者数は小学生の入館者数の2倍であり、
大人の入館者数は小学生、中学生、高校生の合計入館者数よりも100人少なかった。
この日の小学生の入館者数を$x$人、大人の入館者数を$y$人とするとき、次の問いに答えよ。
①この日の総入館者数を$x$と$y$の両方を用いて表せ。
②さらに、この博物館では1個550円のおみやげを売っており、総入館者数の8割の人が購入した。
この日の総入館者の入館料の合計とおみやげの売上げをあわせた金額は150000円で、おみやげを2個以上買った人はいなかった。
このとき$x$と$y$の値をそれぞれ求めよ。
#1 数検準1級一次過去問 連立方程式

単元:
#連立方程式#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#ユークリッド互除法と不定方程式・N進法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
3^{x+1}-2・3^y=-9 \\
\log_2 (x+1)-\log_2 (y+2)=-1
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\boxed{1}$これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
3^{x+1}-2・3^y=-9 \\
\log_2 (x+1)-\log_2 (y+2)=-1
\end{array}
\right.
\end{eqnarray}$
【中学数学】連立方程式の演習~愛媛県公立高校入試2019~【高校受験】

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
花子さんが住む市の1ヵ月の水道料金は、使用量が8m³までは基本料金のみであり、
使用量が8㎡を超えると、超えた使用量に対して1m³当たりいくらかの超過料金が
発生する。
今月から水道料金が値上げされ、先月に比べて、基本料金が20%、1㎡当たりの
超過料金が15円、それぞれ高くなった。
花子さんの家の使用量は先月も今月も25m³であった。
先月の水道料金は4260円であり、今月の水道料金は先月の水道料金と比べると
495円高くなった。
先月の基本料金と、先月の1m³当たりの超過料金をそれぞれ求めよ。
この動画を見る
花子さんが住む市の1ヵ月の水道料金は、使用量が8m³までは基本料金のみであり、
使用量が8㎡を超えると、超えた使用量に対して1m³当たりいくらかの超過料金が
発生する。
今月から水道料金が値上げされ、先月に比べて、基本料金が20%、1㎡当たりの
超過料金が15円、それぞれ高くなった。
花子さんの家の使用量は先月も今月も25m³であった。
先月の水道料金は4260円であり、今月の水道料金は先月の水道料金と比べると
495円高くなった。
先月の基本料金と、先月の1m³当たりの超過料金をそれぞれ求めよ。
【高校受験対策/数学】死守61

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#平方根#1次関数#2次関数#文字と式#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守6
①$-5+2$を計算しなさい。
➁$6 \times \frac{2a+1}{3}$を計算しなさい。
③$(\sqrt{7}-1)(\sqrt{7}+1)$を計算しなさい。
④連立方程式を解きなさい。
$y=x+6$
$y=-2x+3$
⑤2次方程式$x^2-3x-2=0$を解きなさい。
⑥1辺の長さが$x$ cmの正方形が あります。
この正方形の周の長さを$y$ cmとするとき、$y$を$x$の式で表しなさい。
⑦34人の団体Xと40人の団体Yが博物館に行きます。
この博物館の1人分の入館料は$a$円で、40人以上の団体の入館料は20%引きになります。
このとき、団体Xと団体Yでは入館料の合計はどちらが多くかかりますか。
その理由をことばや式を用いて書きなさい。ただし消費税は考えないものとする。
⑧右の図で、3点、A、B、Cは円$o$の周上にあります。 このとき$\angle x$の大きさを求めなさい。
⑨右下の図のような長方形ABCDの紙を、 頂点Aが頂点Cに重なるように折ったときの折り目の線分を作図によって求めなさい。
ただし、作図には定規とコンパスを用い作図に使った線は消さないでおくこと。
この動画を見る
高校受験対策・死守6
①$-5+2$を計算しなさい。
➁$6 \times \frac{2a+1}{3}$を計算しなさい。
③$(\sqrt{7}-1)(\sqrt{7}+1)$を計算しなさい。
④連立方程式を解きなさい。
$y=x+6$
$y=-2x+3$
⑤2次方程式$x^2-3x-2=0$を解きなさい。
⑥1辺の長さが$x$ cmの正方形が あります。
この正方形の周の長さを$y$ cmとするとき、$y$を$x$の式で表しなさい。
⑦34人の団体Xと40人の団体Yが博物館に行きます。
この博物館の1人分の入館料は$a$円で、40人以上の団体の入館料は20%引きになります。
このとき、団体Xと団体Yでは入館料の合計はどちらが多くかかりますか。
その理由をことばや式を用いて書きなさい。ただし消費税は考えないものとする。
⑧右の図で、3点、A、B、Cは円$o$の周上にあります。 このとき$\angle x$の大きさを求めなさい。
⑨右下の図のような長方形ABCDの紙を、 頂点Aが頂点Cに重なるように折ったときの折り目の線分を作図によって求めなさい。
ただし、作図には定規とコンパスを用い作図に使った線は消さないでおくこと。
【エナドリ!】連立方程式:久留米大学附設高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#久留米大学附設高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 久留米大学附設高等学校
次の問いに答えよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{1}{2x-3y}+\displaystyle \frac{2}{x+2y}=3 \\
\displaystyle \frac{3}{2x-3y}+\displaystyle \frac{2}{x+2y}=5
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
この動画を見る
入試問題 久留米大学附設高等学校
次の問いに答えよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{1}{2x-3y}+\displaystyle \frac{2}{x+2y}=3 \\
\displaystyle \frac{3}{2x-3y}+\displaystyle \frac{2}{x+2y}=5
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
【キミのやり方であっている!】連立方程式:関西学院高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#関西学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 関西学院高等学校
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3(\displaystyle \frac{ 5 }{6}x+\displaystyle \frac{ 14 }{3})-5(\displaystyle \frac{ 1 }{3}y-\displaystyle \frac{ 14 }{5})=33 \\
2(\displaystyle \frac{ 5 }{6}x+\displaystyle \frac{ 14 }{3})-5(\displaystyle \frac{ 1 4}{5}-\displaystyle \frac{ 1 }{3}y)=-3
\end{array}
\right.
\end{eqnarray}$
を解け。
この動画を見る
入試問題 関西学院高等学校
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3(\displaystyle \frac{ 5 }{6}x+\displaystyle \frac{ 14 }{3})-5(\displaystyle \frac{ 1 }{3}y-\displaystyle \frac{ 14 }{5})=33 \\
2(\displaystyle \frac{ 5 }{6}x+\displaystyle \frac{ 14 }{3})-5(\displaystyle \frac{ 1 4}{5}-\displaystyle \frac{ 1 }{3}y)=-3
\end{array}
\right.
\end{eqnarray}$
を解け。
【ルーチン】連立方程式の解き方《後編》~【行列のできる】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
【ルーチン】連立方程式の解き方《後編》
$\begin{eqnarray}
\left\{
\begin{array}{l}
ax + by = l \\
cx + dy = m
\end{array}
\right.
\end{eqnarray}$
$ \iff $ $ \begin{pmatrix}
a & b \\
c & d
\end{pmatrix} $$\dbinom{ x }{ y }=\dbinom{ l }{ m }$
この動画を見る
【ルーチン】連立方程式の解き方《後編》
$\begin{eqnarray}
\left\{
\begin{array}{l}
ax + by = l \\
cx + dy = m
\end{array}
\right.
\end{eqnarray}$
$ \iff $ $ \begin{pmatrix}
a & b \\
c & d
\end{pmatrix} $$\dbinom{ x }{ y }=\dbinom{ l }{ m }$
【ルーチン】連立方程式の解き方《前編》~【行列のできる】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
【ルーチン】連立方程式の解き方《前編》
$ \begin{eqnarray}
\left\{
\begin{array}{l}
ax + by+cz = l \\
dx + ey +fz= m \\
gx + hy +i3z= n
\end{array}
\right.
\end{eqnarray}$
この動画を見る
【ルーチン】連立方程式の解き方《前編》
$ \begin{eqnarray}
\left\{
\begin{array}{l}
ax + by+cz = l \\
dx + ey +fz= m \\
gx + hy +i3z= n
\end{array}
\right.
\end{eqnarray}$
【中学数学】連立方程式の文章題基礎~受験問題で演習~ 2-3【中2数学】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
ある店では、チョコレート1個54円、あめが1個81円で売られている。
また、1個の重さは、チョコレートが20g、あめが12gである。
このチョコレートとあめをそれぞれ何個か買ったところ、代金は全部で432円、
全体の重さは124gであった。
チョコレートとあめをそれぞれ何個買ったか求めよ。
2⃣
ある中学校でボランティア活動に参加したことがある生徒は、1年生では1年生
全体の25%、2年生では2年生全体の30%、3年生では3年生全体の40%で、学校全体
では生徒全体の32%である。
また、この中学校の生徒数は、3年生は2年生より15人多く、1年生は240人である。
この中学校の2年生と3年生の生徒数を求めよ。
3⃣
2けたの自然数がある。
この自然数の十の位の数と一の位の数の和は、一の位の数の4倍よりも8小さい。
また、十の位の数と一の位の数を入れかえてできる2けたの自然数と、もとの
自然数との和は132である。もとの自然数を求めよ。
この動画を見る
1⃣
ある店では、チョコレート1個54円、あめが1個81円で売られている。
また、1個の重さは、チョコレートが20g、あめが12gである。
このチョコレートとあめをそれぞれ何個か買ったところ、代金は全部で432円、
全体の重さは124gであった。
チョコレートとあめをそれぞれ何個買ったか求めよ。
2⃣
ある中学校でボランティア活動に参加したことがある生徒は、1年生では1年生
全体の25%、2年生では2年生全体の30%、3年生では3年生全体の40%で、学校全体
では生徒全体の32%である。
また、この中学校の生徒数は、3年生は2年生より15人多く、1年生は240人である。
この中学校の2年生と3年生の生徒数を求めよ。
3⃣
2けたの自然数がある。
この自然数の十の位の数と一の位の数の和は、一の位の数の4倍よりも8小さい。
また、十の位の数と一の位の数を入れかえてできる2けたの自然数と、もとの
自然数との和は132である。もとの自然数を求めよ。
【その本質を調べることも数学】連立方程式:滋賀県高校入試~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#滋賀県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 滋賀県の高校
次の問いに答えよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x - 3y = 1 \\
3x + 2y = 8
\end{array}
\right.
\end{eqnarray}$
連立方程式を解きなさい。
この動画を見る
入試問題 滋賀県の高校
次の問いに答えよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x - 3y = 1 \\
3x + 2y = 8
\end{array}
\right.
\end{eqnarray}$
連立方程式を解きなさい。
【高校受験対策/数学】死守60

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#空間図形#1次関数#平行と合同#確率#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守605-41
①$-5-(-7)$を計算しなさい。
➁$(\frac{1}{4}-\frac{2}{3})\times 12$を計算しなさい。
③$4x \times\frac{2}{5}xy \div 2x^2$を計算しなさい。
④$(-2a+3)(2a+3)+9$を計算しなさい。
⑤$\sqrt{24} \div \sqrt{8}-\sqrt{12}$を計算しなさい。
⑥$150$を素因数分解しなさい。
⑦次の連立方程式を解きなさい。
$y=4(x+2)$
$6x-y=-10$
⑧次の数量の関係を等式で表しなさい。
100円硬貨が$a$ 枚、50円硬貨が$b$ 枚あり、これらをすべて10円硬貨に両替すると$c$ 枚になる。
⑨箱の中に同じ大きさの白玉がたくさん入っている。
そこに同じ大きさの黒玉100個入れてよくかき混ぜた後、その中から34個の玉を無作為に取りだしたところ、黒玉が4個入っていた。
この結果から、箱の中にはおよそ何個の白玉が入っていると考えられるか求めなさい。
➉半径6cmの球を中心$o$を通る平面で切った半球の表面積を求めなさい。
⑪右の図で$l /\!/ m$、$AB=AC$のとき、$\angle x$ の大きさを求めなさい。
この動画を見る
高校受験対策・死守605-41
①$-5-(-7)$を計算しなさい。
➁$(\frac{1}{4}-\frac{2}{3})\times 12$を計算しなさい。
③$4x \times\frac{2}{5}xy \div 2x^2$を計算しなさい。
④$(-2a+3)(2a+3)+9$を計算しなさい。
⑤$\sqrt{24} \div \sqrt{8}-\sqrt{12}$を計算しなさい。
⑥$150$を素因数分解しなさい。
⑦次の連立方程式を解きなさい。
$y=4(x+2)$
$6x-y=-10$
⑧次の数量の関係を等式で表しなさい。
100円硬貨が$a$ 枚、50円硬貨が$b$ 枚あり、これらをすべて10円硬貨に両替すると$c$ 枚になる。
⑨箱の中に同じ大きさの白玉がたくさん入っている。
そこに同じ大きさの黒玉100個入れてよくかき混ぜた後、その中から34個の玉を無作為に取りだしたところ、黒玉が4個入っていた。
この結果から、箱の中にはおよそ何個の白玉が入っていると考えられるか求めなさい。
➉半径6cmの球を中心$o$を通る平面で切った半球の表面積を求めなさい。
⑪右の図で$l /\!/ m$、$AB=AC$のとき、$\angle x$ の大きさを求めなさい。
【数学はパズルだ!】連立方程式:愛知県高校入試~全国入試問題解法
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
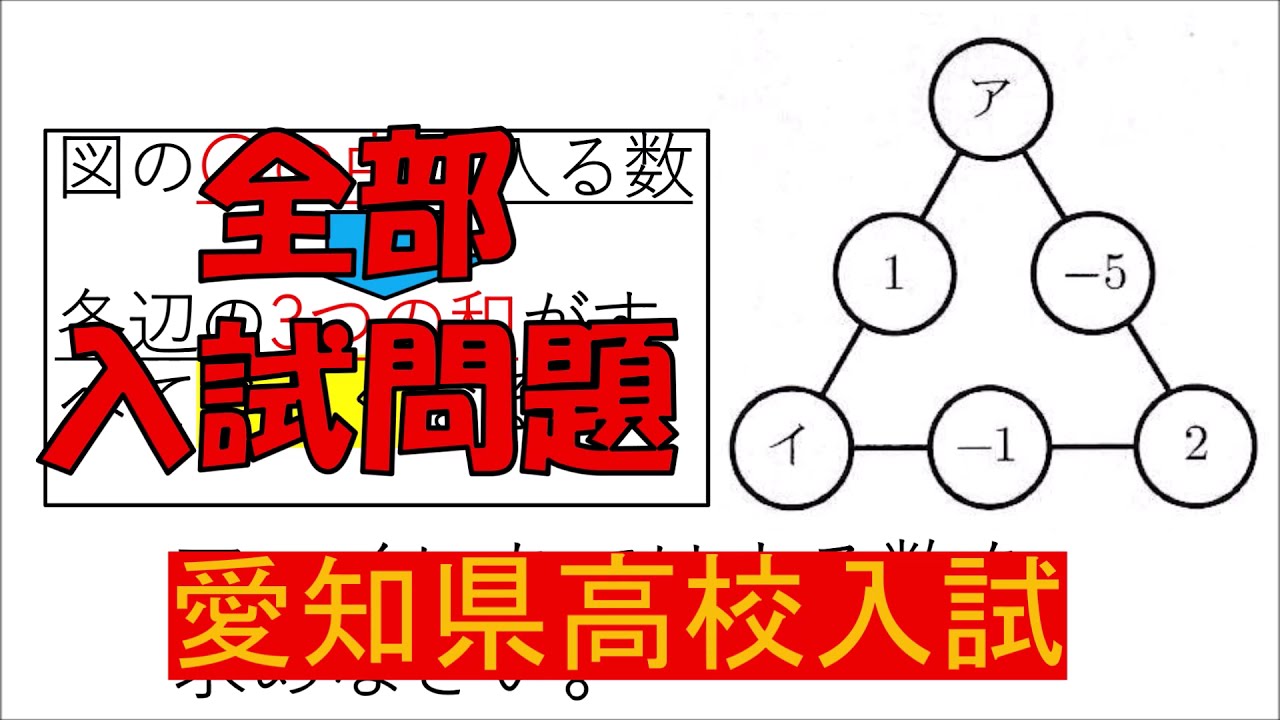
入試問題 愛知県の高校
図の○の中に入る数
各辺の3つの和がすべて等しくなる。
ア、イにあてはまる数を求めなさい。
この動画を見る
入試問題 愛知県の高校
図の○の中に入る数
各辺の3つの和がすべて等しくなる。
ア、イにあてはまる数を求めなさい。
連立方程式解法~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連立方程式解法~全国入試問題解法
次の連立方程式を解け。
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x + 2y + z = 3 \\
3x + y + 4z= 5 \\
2x+y+3z=4
\end{array}
\right.
\end{eqnarray}$
※高校入試では出ませんので、 念のため・・・。
この動画を見る
連立方程式解法~全国入試問題解法
次の連立方程式を解け。
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x + 2y + z = 3 \\
3x + y + 4z= 5 \\
2x+y+3z=4
\end{array}
\right.
\end{eqnarray}$
※高校入試では出ませんので、 念のため・・・。
【現実は厳しい?】連立方程式:早稲田大学系属早稲田実業学校高等部~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 早稲田大学系属早稲田実業学校高等部
$\begin{eqnarray}
\left\{
\begin{array}{l}
Ax + By = 12 ・・・(ァ)\\
Bx-Ay = 16 ・・・(イ)\\
6x-8y=C ・・・(ウ)\\
Dx-6y=E ・・・(エ) \\
\end{array}
\right.
\end{eqnarray}$
条件Ⅰ:アとウを連立→解なし。
条件Ⅱ:アとエを連立→解:$x=8,y=9$
条件Ⅲ:「ウとエを連立した解」
→「アとイを連立した解」
よりの値は$6$大きく、$y$の値は$2$大きい。
①$A,B$の値をそれぞれ求めよ。
②$C.E$の値をそれぞれ求めよ。
この動画を見る
入試問題 早稲田大学系属早稲田実業学校高等部
$\begin{eqnarray}
\left\{
\begin{array}{l}
Ax + By = 12 ・・・(ァ)\\
Bx-Ay = 16 ・・・(イ)\\
6x-8y=C ・・・(ウ)\\
Dx-6y=E ・・・(エ) \\
\end{array}
\right.
\end{eqnarray}$
条件Ⅰ:アとウを連立→解なし。
条件Ⅱ:アとエを連立→解:$x=8,y=9$
条件Ⅲ:「ウとエを連立した解」
→「アとイを連立した解」
よりの値は$6$大きく、$y$の値は$2$大きい。
①$A,B$の値をそれぞれ求めよ。
②$C.E$の値をそれぞれ求めよ。
連立方程式:立命館高校入試~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 立命館高等学校
次の連立方程式を解きなさい。
$\displaystyle \frac{x+3y}{2}=\displaystyle \frac{2x+6y+2}{3}=-\displaystyle \frac{2}{5}(4x+5y)$
この動画を見る
入試問題 立命館高等学校
次の連立方程式を解きなさい。
$\displaystyle \frac{x+3y}{2}=\displaystyle \frac{2x+6y+2}{3}=-\displaystyle \frac{2}{5}(4x+5y)$
【高校受験対策/数学】死守58

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式#比例・反比例#空間図形#1次関数#文字と式#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守58 @397
①$5-8$を計算せよ
②$-4 \times(-3)^2$を計算せよ。
③$(4a^2b+6ab^2)\div 2ab$を計算せよ。
④$(x+y)^2-5xy$を計算せよ。
⑤絶対値が$4$より小さい整数は何個あるか。
⑥2次方程式$x^2+5x+2=0$を解け。
⑦$y$が$x$に反比例し、$x$と$y$の値が下の表のように対応しているとき、表のAに当てはまる数を求めよ。
⑧図1は円すいの展開図で、底面の半径は$5cm$、側面のおうぎ形の半径は$12cm$である。
$\angle x$の大きさを求めなさい。
⑨一の位の数が0でない、2桁の自然数Aがある。
Aの十の位の数とーの位の数を入れかえてできる数をBとする。
Aの十の位の数は一の位の数の2倍であり、BはAより36小さい。このときAの値を求めよ。
⑩右の表はある市における、7月の日ごとの最高気温を度数分布表にまとめたものである。
この表から読み取ることができることがらとして適切なものを、次のア~オからすべて選べ。
ア $32.0℃$以上$34.0℃$未満の階緑の相対度数は$0.16$よりきい。
イ 階級の幅は$12.0℃$である。
ウ 最高気温が$28.0℃$以上の日は、$5$日である。
エ 最頻値(モード)は、$27.0℃$である。
オ $30.0℃$以上$32.0℃$未満の階級の階級値は、$30.0℃$である。
この動画を見る
高校受験対策・死守58 @397
①$5-8$を計算せよ
②$-4 \times(-3)^2$を計算せよ。
③$(4a^2b+6ab^2)\div 2ab$を計算せよ。
④$(x+y)^2-5xy$を計算せよ。
⑤絶対値が$4$より小さい整数は何個あるか。
⑥2次方程式$x^2+5x+2=0$を解け。
⑦$y$が$x$に反比例し、$x$と$y$の値が下の表のように対応しているとき、表のAに当てはまる数を求めよ。
⑧図1は円すいの展開図で、底面の半径は$5cm$、側面のおうぎ形の半径は$12cm$である。
$\angle x$の大きさを求めなさい。
⑨一の位の数が0でない、2桁の自然数Aがある。
Aの十の位の数とーの位の数を入れかえてできる数をBとする。
Aの十の位の数は一の位の数の2倍であり、BはAより36小さい。このときAの値を求めよ。
⑩右の表はある市における、7月の日ごとの最高気温を度数分布表にまとめたものである。
この表から読み取ることができることがらとして適切なものを、次のア~オからすべて選べ。
ア $32.0℃$以上$34.0℃$未満の階緑の相対度数は$0.16$よりきい。
イ 階級の幅は$12.0℃$である。
ウ 最高気温が$28.0℃$以上の日は、$5$日である。
エ 最頻値(モード)は、$27.0℃$である。
オ $30.0℃$以上$32.0℃$未満の階級の階級値は、$30.0℃$である。
連立方程式はもっと楽に解こうよ

【高校受験対策/数学】死守57

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#確率
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守57
①$6\times (-3)$を計算しなさい。
②$9-(-4)^2 \times \frac{5}{8}$を計算しなさい。
③$a^2b×21b \div 7a$を計算しなさい。
④連立方程式
$0.2x+1.5y=4$
$x-3y=-1$を解きなさい。
⑤$\frac{12}{\sqrt{3}}-3\sqrt{6} \times \sqrt{8}$を計算しなさい。
⑥二次方程式$x^2+5x+5=0$を解きなさい。
⑦ある美術館の入館料は、おとな1人が$a$円、中学生1人が$b$円である。
このとき、不等式$2a+3b \gt 2000$が表している数量の関係として最も適当なものを、次のア~エのうちから1つ選び、符号で答えなさい。
ア おとな2人と中学生3人の入館料の合計は、2000円より安い。
イ おとな2人と中学生3人の入館料の合計は、2000円より高い。
ウ おとな2人と中学生3人の入館料の合計は、2000円以下である。
エ おとな2人と中学生3人の入館料の合計は、2000円以上である。
⑧-5、-2、-1、3、6、10の整数が1つずつ書かれた6枚のカードがある。
この6枚のカードをよくきって、同時に2枚ひく。
このとき、ひいた2枚のカードに書かれた数の平均値が、自然数になる確率を求めなさい。
ただし、どのカードをひくことも同様に確からしいものとする。
この動画を見る
高校受験対策・死守57
①$6\times (-3)$を計算しなさい。
②$9-(-4)^2 \times \frac{5}{8}$を計算しなさい。
③$a^2b×21b \div 7a$を計算しなさい。
④連立方程式
$0.2x+1.5y=4$
$x-3y=-1$を解きなさい。
⑤$\frac{12}{\sqrt{3}}-3\sqrt{6} \times \sqrt{8}$を計算しなさい。
⑥二次方程式$x^2+5x+5=0$を解きなさい。
⑦ある美術館の入館料は、おとな1人が$a$円、中学生1人が$b$円である。
このとき、不等式$2a+3b \gt 2000$が表している数量の関係として最も適当なものを、次のア~エのうちから1つ選び、符号で答えなさい。
ア おとな2人と中学生3人の入館料の合計は、2000円より安い。
イ おとな2人と中学生3人の入館料の合計は、2000円より高い。
ウ おとな2人と中学生3人の入館料の合計は、2000円以下である。
エ おとな2人と中学生3人の入館料の合計は、2000円以上である。
⑧-5、-2、-1、3、6、10の整数が1つずつ書かれた6枚のカードがある。
この6枚のカードをよくきって、同時に2枚ひく。
このとき、ひいた2枚のカードに書かれた数の平均値が、自然数になる確率を求めなさい。
ただし、どのカードをひくことも同様に確からしいものとする。
【高校受験対策/数学】死守55

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#空間図形#2次関数#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守55
①$(-3)^2+2 \times (-5)$を計算しなさい。
②$\frac{4x-3}{2}\times\frac{6x-7}{5}$を計算しなさい。
③$(-4xy)^2×(-3x)$を計算しなさい。
④連立方程式を解きなさい。
$4x-3y=-7$
$5x+9y=-13$
⑤$5\sqrt{6}+2\sqrt{24}-\frac{6\sqrt{3}}{\sqrt{2}}$を計算しなさい。
⑥二次方程式$(x+4)(x-6)=6x-39$を解きなさい。
②関数$y=ax^2$について、$x$の値が$-5$から$-3$まで増加したときの変化の割合が$2$であるとき、$a$の値を求めなさい。
⑧底面の半径が$5$ cm、高さが$6$ cmの円すいの体積を求めなさい。 ただし円周率は$\pi$とする。
⑨右の図1のように、三角形$ABC$の$\angle B$の二等分線と$\angle C$の外角$\angle ACD$の二等分線の交点を$E$とする。
$\angle BAC$の大きさが$40°$のとき、$\angle BEC$の大きさを求めなさい。
⑩右の図2で、$\angle APB=120°$のひし形$AQBP$を1つ、 定規とコンパスを用いて作図しなさい。 なお作図に用いた線は消さずに残して おきなさい。
この動画を見る
高校受験対策・死守55
①$(-3)^2+2 \times (-5)$を計算しなさい。
②$\frac{4x-3}{2}\times\frac{6x-7}{5}$を計算しなさい。
③$(-4xy)^2×(-3x)$を計算しなさい。
④連立方程式を解きなさい。
$4x-3y=-7$
$5x+9y=-13$
⑤$5\sqrt{6}+2\sqrt{24}-\frac{6\sqrt{3}}{\sqrt{2}}$を計算しなさい。
⑥二次方程式$(x+4)(x-6)=6x-39$を解きなさい。
②関数$y=ax^2$について、$x$の値が$-5$から$-3$まで増加したときの変化の割合が$2$であるとき、$a$の値を求めなさい。
⑧底面の半径が$5$ cm、高さが$6$ cmの円すいの体積を求めなさい。 ただし円周率は$\pi$とする。
⑨右の図1のように、三角形$ABC$の$\angle B$の二等分線と$\angle C$の外角$\angle ACD$の二等分線の交点を$E$とする。
$\angle BAC$の大きさが$40°$のとき、$\angle BEC$の大きさを求めなさい。
⑩右の図2で、$\angle APB=120°$のひし形$AQBP$を1つ、 定規とコンパスを用いて作図しなさい。 なお作図に用いた線は消さずに残して おきなさい。
【高校受験対策/数学】死守53

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守53
①$2-(-9)$を計算せよ。
②$52a^2b \div (-4a)$を計算せよ。
③$\sqrt{28}+\frac{49}{\sqrt{7}}$を計算せよ。
④$\frac{3x-y}{3}-\frac{x-2y}{4}$を計算せよ。
⑤$(\sqrt{2}+1)^2-5({\sqrt{2}+1)}+4$を計算せよ。
⑥2次方程式$x^2-5x-3=0$を解きなさい。
⑦関数$y=-\frac{1}{3}x^2$について、$x$の値が$3$から$6$まで増加するときの変化の割合を求めなさい。
⑧連立方程式
$ax+by=10$
$bx-ay=5$
の解が$x=2$、$y=1$であるとき$a$、$b$の値を求めなさい。
⑨ある動物園では、大人1人の入園料が子ども1人の入園料より600円高い。
大人1人の入園料と子ども 1人の入園料の比が$5:2$であるとき、子ども1人の入園料を求めなさい。
⑩$\frac{5880}{n}$が自然数の平方となるような、最も小さい自然数$n$の値を求めなさい。
この動画を見る
高校受験対策・死守53
①$2-(-9)$を計算せよ。
②$52a^2b \div (-4a)$を計算せよ。
③$\sqrt{28}+\frac{49}{\sqrt{7}}$を計算せよ。
④$\frac{3x-y}{3}-\frac{x-2y}{4}$を計算せよ。
⑤$(\sqrt{2}+1)^2-5({\sqrt{2}+1)}+4$を計算せよ。
⑥2次方程式$x^2-5x-3=0$を解きなさい。
⑦関数$y=-\frac{1}{3}x^2$について、$x$の値が$3$から$6$まで増加するときの変化の割合を求めなさい。
⑧連立方程式
$ax+by=10$
$bx-ay=5$
の解が$x=2$、$y=1$であるとき$a$、$b$の値を求めなさい。
⑨ある動物園では、大人1人の入園料が子ども1人の入園料より600円高い。
大人1人の入園料と子ども 1人の入園料の比が$5:2$であるとき、子ども1人の入園料を求めなさい。
⑩$\frac{5880}{n}$が自然数の平方となるような、最も小さい自然数$n$の値を求めなさい。
