 1次関数
1次関数
 1次関数
1次関数
中2数学「2直線の交点の求め方」【毎日配信】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~2直線の交点の求め方
例1 y = - x + 3と =2x-3の交点の座標を求めなさい。
例2 y = 3分の1 x - 2と、y =2x+3の交点の座標を求めなさい。
この動画を見る
中2~2直線の交点の求め方
例1 y = - x + 3と =2x-3の交点の座標を求めなさい。
例2 y = 3分の1 x - 2と、y =2x+3の交点の座標を求めなさい。
中2数学「1次関数の変域問題②」【毎日配信】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~1次関数の変域問題②~
例1 グラフが右下がりの直線で、xの変域が2≤x≤4 のとき、yの変域が5≦y≦7である1次関数の式を 求めなさい。
例2 傾きが負の数の1次関数y=ax+8は、xの変域が −2≦X≦1のとき、yの変域はb≦y≦11です。 a.bの値を求めなさい。
この動画を見る
中2~1次関数の変域問題②~
例1 グラフが右下がりの直線で、xの変域が2≤x≤4 のとき、yの変域が5≦y≦7である1次関数の式を 求めなさい。
例2 傾きが負の数の1次関数y=ax+8は、xの変域が −2≦X≦1のとき、yの変域はb≦y≦11です。 a.bの値を求めなさい。
中2数学「1次関数の変域問題①」【毎日配信】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~1次関数の変域問題①~
例1 y=x+3において、xの変域が1≦x≦4のときの Yの変域を求めなさい。
例2 y=-2x+1において、xの変域が-3≦x≦2のときの yの変域を求めなさい。
この動画を見る
中2~1次関数の変域問題①~
例1 y=x+3において、xの変域が1≦x≦4のときの Yの変域を求めなさい。
例2 y=-2x+1において、xの変域が-3≦x≦2のときの yの変域を求めなさい。
中2数学「1次関数の式の求め方⑤(x軸で交わる)」【毎日配信】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~1次関数の式の求め方⑤~ (X軸で交わる)
例題次の直線や1次関数の式を求めなさい。
(1) 傾きが2で、y=-x+3とX軸で交わる直線
(2)(1,-4)を通り、y=2x+6とX軸で交わる直線
この動画を見る
中2~1次関数の式の求め方⑤~ (X軸で交わる)
例題次の直線や1次関数の式を求めなさい。
(1) 傾きが2で、y=-x+3とX軸で交わる直線
(2)(1,-4)を通り、y=2x+6とX軸で交わる直線
中2数学「1次関数の式の求め方④(2点の座標)」【毎日配信】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~1次関数の式の求め方④~ (2点の座標)
例題次の直線や1次関数の式を求めなさい。
(1)2点(-1,1)(1,3)を通る直線
(2)X=-1のときy=10,x=3のときy=2である1次関数
この動画を見る
中2~1次関数の式の求め方④~ (2点の座標)
例題次の直線や1次関数の式を求めなさい。
(1)2点(-1,1)(1,3)を通る直線
(2)X=-1のときy=10,x=3のときy=2である1次関数
中2数学「1次関数の式の求め方③(切片と座標)」【毎日配信】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~1次関数の式の求め方 ③~
例題次の直線の式を求めなさい。
(1)切片が2で(3,-1)を通る直線
(2)直線y=-x-3とり軸上で交わり、(2,1)を通る直線
(3)2点(0,5)(6,3)を通る直線
この動画を見る
中2~1次関数の式の求め方 ③~
例題次の直線の式を求めなさい。
(1)切片が2で(3,-1)を通る直線
(2)直線y=-x-3とり軸上で交わり、(2,1)を通る直線
(3)2点(0,5)(6,3)を通る直線
中2数学「1次関数の式の求め方②(傾きと座標)」【毎日配信】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~1次関数の式の求め方②~
例題次の直線や1次関数の式を求めなさい。
(1) 傾きが2で、(-1,-5)を通る直線
(2)変化の割合が-3で、X=-2のときy=1である1次関数
(3)Xが2増加すると、yは4減少し、x=-1のときy=6である 1次関数
(4)直線y=-2x+7に平行で、(-4.3)を通る直線
この動画を見る
中2~1次関数の式の求め方②~
例題次の直線や1次関数の式を求めなさい。
(1) 傾きが2で、(-1,-5)を通る直線
(2)変化の割合が-3で、X=-2のときy=1である1次関数
(3)Xが2増加すると、yは4減少し、x=-1のときy=6である 1次関数
(4)直線y=-2x+7に平行で、(-4.3)を通る直線
中2数学「1次関数の式の求め方①(グラフからの読み取り)」【毎日配信】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~1次関数の式の求め方①~ (グラフからの読み取り )
例題次の図の直線の式を求めなさい。
この動画を見る
中2~1次関数の式の求め方①~ (グラフからの読み取り )
例題次の図の直線の式を求めなさい。
中2数学「1次関数のグラフの書き方②」【毎日配信】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~1次関数のグラフの書き方②~
例題次のグラフを書きなさい。
(1)x = - 2(2) y = 3
(3) 2y = - 8(4) 2x - 5 = 3
この動画を見る
中2~1次関数のグラフの書き方②~
例題次のグラフを書きなさい。
(1)x = - 2(2) y = 3
(3) 2y = - 8(4) 2x - 5 = 3
中2数学「1次関数のグラフの書き方①」【毎日配信】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~1次関数のグラフの書き方①~
例題次の1次関数のグラフを書きなさい。
(1) y = 2x - 3 (2) y = - 3/4 x + 2
(3) x/2 - y/3 = 1 (4) X-3y=7
この動画を見る
中2~1次関数のグラフの書き方①~
例題次の1次関数のグラフを書きなさい。
(1) y = 2x - 3 (2) y = - 3/4 x + 2
(3) x/2 - y/3 = 1 (4) X-3y=7
中2数学「変化の割合」【毎日配信】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~変化の割合~ ・・変化の割合とは?
例1 y=-5X-1について、次の問いに答えなさい。
(1)変化の割合を答えなさい。
(2)Xの値が2から4まで増加するときの yの増加量を求めなさい。
この動画を見る
中2~変化の割合~ ・・変化の割合とは?
例1 y=-5X-1について、次の問いに答えなさい。
(1)変化の割合を答えなさい。
(2)Xの値が2から4まで増加するときの yの増加量を求めなさい。
中2数学「1次関数の式」【毎日配信】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
中2~1次関数の式
例1 yがxの1次関数であるものをすべて選びなさい。
例2次のxとyの関係について、yをxの式で表しなさい。また、yが1次関数であるものをすべて選びなさい。
(1)120円のりんごを火個買ったときの代金y円
(2) 10kmを歩くとき、歩いた道のりXkmと残りの道のりykm
(3)面積が48cmの長方形の縦Xcm、横ycm
この動画を見る
中2~1次関数の式
例1 yがxの1次関数であるものをすべて選びなさい。
例2次のxとyの関係について、yをxの式で表しなさい。また、yが1次関数であるものをすべて選びなさい。
(1)120円のりんごを火個買ったときの代金y円
(2) 10kmを歩くとき、歩いた道のりXkmと残りの道のりykm
(3)面積が48cmの長方形の縦Xcm、横ycm
発想の転換な動体視力と数学~全国入試問題解法 #Shorts
単元:
#数学(中学生)#中2数学#1次関数
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
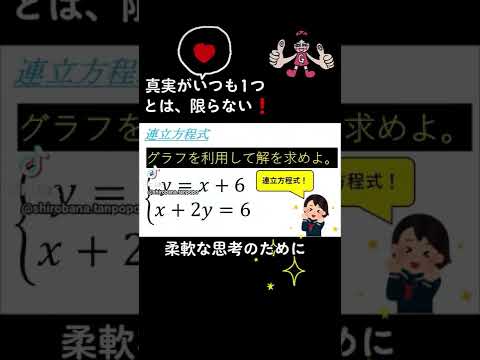
グラフを利用して解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
y=x+6 \\
x+2y=6
\end{array}
\right.
\end{eqnarray}$
青森県高校過去問
この動画を見る
グラフを利用して解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
y=x+6 \\
x+2y=6
\end{array}
\right.
\end{eqnarray}$
青森県高校過去問
なんとなくの雰囲気で変域の問題を解くと間違える 日比谷高校 2022入試問題100題解説67問目!! オープニング失敗!

単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
1次関数$y=ax+4$においてxの変域が$-3 \leqq x \leqq 6$のとき
yの変域が$2 \leqq y \leqq 5$である。
定数aの値を求めよ。
2022日比谷高等学校
この動画を見る
1次関数$y=ax+4$においてxの変域が$-3 \leqq x \leqq 6$のとき
yの変域が$2 \leqq y \leqq 5$である。
定数aの値を求めよ。
2022日比谷高等学校
動体視力と数学を鍛える動画~全国入試問題解法 #Shorts
単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
点$P$の座標を求めなさい.
東京学芸大附属高校過去問
この動画を見る
点$P$の座標を求めなさい.
東京学芸大附属高校過去問
高等学校入試予想問題:宮崎県~全国入試問題解法

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#1次関数#確率#2次関数#三角形と四角形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\boxed{1}$
(1)$27xy\times x^2\div(-9x^2y)$を計算せよ.
(2)$3(x+6y)-2(x+8y)$を計算せよ.
(3)$y$は$x$に比例し,$x=-3$のとき,$y=36$である.
このとき,$y$を$x$の式で表せ.
(4)箱の中に4本のくじ,そのうち3本が当たり.
Aさんが1本引いて戻す.同様にBさんが引く.
2人共,当たりくじをひく確率は?
$\boxed{2}$
$y=x^2$上に$A(2,4)$である.
点$B$は$y$軸上,$y$座標が4より大きい範囲で動く.
$C,D$は,$B$を通り,$x$軸と平行な直線と$y=x^2$の交点である.
(1)点$E$の$x$座標が5となるとき,$\triangle AOE$の面積は?
(2)$CA=AE$となるとき,直線$DE$の傾きは?
$\boxed{3}$
(1)$\triangle AED \backsim \triangle CFD$であることの証明をせよ.
(2)$AE=&,EB=5,BC=2,CF=8$のとき,
①$AC=?$ ②$AD=?$ ③$DF=?$ ④$\Box ABFD$の面積は?
この動画を見る
$\boxed{1}$
(1)$27xy\times x^2\div(-9x^2y)$を計算せよ.
(2)$3(x+6y)-2(x+8y)$を計算せよ.
(3)$y$は$x$に比例し,$x=-3$のとき,$y=36$である.
このとき,$y$を$x$の式で表せ.
(4)箱の中に4本のくじ,そのうち3本が当たり.
Aさんが1本引いて戻す.同様にBさんが引く.
2人共,当たりくじをひく確率は?
$\boxed{2}$
$y=x^2$上に$A(2,4)$である.
点$B$は$y$軸上,$y$座標が4より大きい範囲で動く.
$C,D$は,$B$を通り,$x$軸と平行な直線と$y=x^2$の交点である.
(1)点$E$の$x$座標が5となるとき,$\triangle AOE$の面積は?
(2)$CA=AE$となるとき,直線$DE$の傾きは?
$\boxed{3}$
(1)$\triangle AED \backsim \triangle CFD$であることの証明をせよ.
(2)$AE=&,EB=5,BC=2,CF=8$のとき,
①$AC=?$ ②$AD=?$ ③$DF=?$ ④$\Box ABFD$の面積は?
【高校受験対策/数学】死守-95

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$2-(-5)-9$を計算せよ。
②$\frac{3x-y}{4}-\frac{x+2y}{3}$を計算せよ。
③$a^2b×(-3b)÷6ab^2$を計算せよ。
④$\frac{12}{\sqrt2}-\sqrt32$を計算せよ 。
⑤50本の鉛筆を、7人の生徒に1人$a$本ずつ配ると、$b$本余った。
このとき、$b$を$a$の式で表せ。
⑥2次方程式$(x-4)(x+2)=3x-2$を解け。
⑦$a$は正の数とする。
次の文字式のうち、式の値が$a$の値よりも小さくなる文字式はどれか。
次のアーエからすべて選び、その記号で書け。
ア $a+(-\frac{1}{2})$
イ $a-(-\frac{1}{2})$
ウ $a×(-\frac{1}{2})$
エ $a÷(-\frac{1}{2})$
⑧関数$y=ax^2$について、$x$の変域が$-2 \leqq x \leqq -1$のとき、
$y$の変域は$-3 \leqq y \leqq 12$である。このときの$a$の値を求めよ。
⑨右の図のように、2つの半直線$AB,AC$があり、半直線$AB$上に点$D$をとる。
2つの半直線$AB,AC$の両方に接する円のうち、 点$D$で半直線$AB$と接する円の中心$P$を定規・コンパスを使い作図によって求めよ。
この動画を見る
①$2-(-5)-9$を計算せよ。
②$\frac{3x-y}{4}-\frac{x+2y}{3}$を計算せよ。
③$a^2b×(-3b)÷6ab^2$を計算せよ。
④$\frac{12}{\sqrt2}-\sqrt32$を計算せよ 。
⑤50本の鉛筆を、7人の生徒に1人$a$本ずつ配ると、$b$本余った。
このとき、$b$を$a$の式で表せ。
⑥2次方程式$(x-4)(x+2)=3x-2$を解け。
⑦$a$は正の数とする。
次の文字式のうち、式の値が$a$の値よりも小さくなる文字式はどれか。
次のアーエからすべて選び、その記号で書け。
ア $a+(-\frac{1}{2})$
イ $a-(-\frac{1}{2})$
ウ $a×(-\frac{1}{2})$
エ $a÷(-\frac{1}{2})$
⑧関数$y=ax^2$について、$x$の変域が$-2 \leqq x \leqq -1$のとき、
$y$の変域は$-3 \leqq y \leqq 12$である。このときの$a$の値を求めよ。
⑨右の図のように、2つの半直線$AB,AC$があり、半直線$AB$上に点$D$をとる。
2つの半直線$AB,AC$の両方に接する円のうち、 点$D$で半直線$AB$と接する円の中心$P$を定規・コンパスを使い作図によって求めよ。
【高校受験対策/数学】死守-92

単元:
#数学(中学生)#中1数学#正の数・負の数#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#平面図形#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守92
①$12÷(-4)$を計算しなさい。
②$\sqrt{3}×\sqrt{8}$を計算しなさい。
③$(x-4)(x-5)$を展開しなさい。
④二次方程式$x^2-5x+3=0$を解きなさい。
⑤$\frac{336}{n}$の値が、ある自然数の2乗となるような自然数$n$のうち、
最も小さいものを求めなさい。
⑥右の表は、ある中学校の生徒30人が1か月に読んだ本の冊数を調べて、度数分布表に整理 したものである。
ただし、一部が汚れて度数が見えなくなっている。
この度数分布表について、3冊以上6冊未満の階級の相対度数を求めなさい。
⑦右の図のように、五角形$ABCDE$があり、$\angle BCD=105°,$$\angle CDE=110°$である。
また、頂点$A,E$における外角$B$の大きさがそれぞれ$70°,80°$であるとき、
$\angle ABC$の大きさを求めなさい。
⑧二次関数$y=\frac{5}{2}x+a$のグラフは点$(4,3)$を通る。
このグラフと$y$軸との交点の座標を求めなさい。
この動画を見る
高校受験対策・死守92
①$12÷(-4)$を計算しなさい。
②$\sqrt{3}×\sqrt{8}$を計算しなさい。
③$(x-4)(x-5)$を展開しなさい。
④二次方程式$x^2-5x+3=0$を解きなさい。
⑤$\frac{336}{n}$の値が、ある自然数の2乗となるような自然数$n$のうち、
最も小さいものを求めなさい。
⑥右の表は、ある中学校の生徒30人が1か月に読んだ本の冊数を調べて、度数分布表に整理 したものである。
ただし、一部が汚れて度数が見えなくなっている。
この度数分布表について、3冊以上6冊未満の階級の相対度数を求めなさい。
⑦右の図のように、五角形$ABCDE$があり、$\angle BCD=105°,$$\angle CDE=110°$である。
また、頂点$A,E$における外角$B$の大きさがそれぞれ$70°,80°$であるとき、
$\angle ABC$の大きさを求めなさい。
⑧二次関数$y=\frac{5}{2}x+a$のグラフは点$(4,3)$を通る。
このグラフと$y$軸との交点の座標を求めなさい。
【高校受験対策/数学】関数-57

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数57
Q.
図1のような、$AB=10cm$、$AD=3cm$の長方形$ABCD$がある。
点$P$は$A$から、点$Q$は$D$から同時に動き出し、
ともに毎秒$1cm$の速さで点$P$は辺$AB$上を、点$Q$は辺$DC$上を繰り返し往復する。
2点$P,Q$が動き出してから、$x$秒後の$\triangle APQ$の面積を$y cm^2$とする。
ただし点$P$が$A$にあるとき、$y=0$とする。
このとき次の各問いに答えなさい。
①2点$P,Q$が動き出してから$6$秒後の$\triangle APQ$の面積を求めなさい。
②図2は、$x$と$y$の関係を表したグラフの一部である。
2点$P,Q$が 動き出して$10$秒後から$20$秒後までの$x$と$y$の関係を式で表しなさい。
③点$R$は$A$に、点$S$は$D$にあり、それぞれ静止している。
2点$P,Q$が動き出してから$10$秒後に、2点$R,S$は動き出し、ともに毎秒$0.5cm$の速さで点$R$は辺$AB$上を、点$S$は辺$DC$上を2点$P,Q$と同様に繰り返し往復する。
このとき2点$P,Q$が動き出してから$t$秒後に$\triangle APQ$の面積と四角形$BCSR$の面積が等しくなった。
このような$t$の値のうち、小さいほうから$3$番目の値を求めなさい。
この動画を見る
高校受験対策・関数57
Q.
図1のような、$AB=10cm$、$AD=3cm$の長方形$ABCD$がある。
点$P$は$A$から、点$Q$は$D$から同時に動き出し、
ともに毎秒$1cm$の速さで点$P$は辺$AB$上を、点$Q$は辺$DC$上を繰り返し往復する。
2点$P,Q$が動き出してから、$x$秒後の$\triangle APQ$の面積を$y cm^2$とする。
ただし点$P$が$A$にあるとき、$y=0$とする。
このとき次の各問いに答えなさい。
①2点$P,Q$が動き出してから$6$秒後の$\triangle APQ$の面積を求めなさい。
②図2は、$x$と$y$の関係を表したグラフの一部である。
2点$P,Q$が 動き出して$10$秒後から$20$秒後までの$x$と$y$の関係を式で表しなさい。
③点$R$は$A$に、点$S$は$D$にあり、それぞれ静止している。
2点$P,Q$が動き出してから$10$秒後に、2点$R,S$は動き出し、ともに毎秒$0.5cm$の速さで点$R$は辺$AB$上を、点$S$は辺$DC$上を2点$P,Q$と同様に繰り返し往復する。
このとき2点$P,Q$が動き出してから$t$秒後に$\triangle APQ$の面積と四角形$BCSR$の面積が等しくなった。
このような$t$の値のうち、小さいほうから$3$番目の値を求めなさい。
時短じゃね?

【中学数学】1次関数の傾きと切片を式変形せずに出す技 3-3【中2数学】

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$5x+2y+7=0$の傾きと切片を求めよ。
2⃣
$2x+3y-8=0$に平行で、点(6,5)を通る直線の式を求めよ。
この動画を見る
1⃣
$5x+2y+7=0$の傾きと切片を求めよ。
2⃣
$2x+3y-8=0$に平行で、点(6,5)を通る直線の式を求めよ。
【高校受験対策/数学】死守82

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#資料の活用#1次関数#文字と式#平面図形#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守82
①$3-(-6)$を計算しなさい。
②$9÷(-\frac{1}{5})+4$を計算しなさい。
③$\sqrt{28}-\sqrt{7}$を計算しなさい。
④下の図のように、半径が$9cm$、中心角が$60°$のおうぎ形$OAB$があります。
このおうぎ形の弧$AB$の長さを求めなさい。
ただし円周率は$\pi$を用いなさい。
⑤右の表は、A中学校の3年生男子80人の立ち幅とびの記録を度数分布表にまと めたものです。
度数が最も多い階級の相対度数を求めなさい。
⑥関数$y=3x$のグラフに平行で、 点$(0,2)$を通る直線の式を求めなさい。
⑦右の図の四角形$ABCD$において、点$B$と点$Dが$重なるように折ったときにできる折り目の線と
辺$AB$、$BC$との交点をそれぞれ$P,Q$とします。
2点$P,Q$を定規とコンパスを使って作図しなさい。
ただし、点を示す記号$P,Q$をかき入れ、作図に用いた線は消さないこと。
この動画を見る
高校受験対策・死守82
①$3-(-6)$を計算しなさい。
②$9÷(-\frac{1}{5})+4$を計算しなさい。
③$\sqrt{28}-\sqrt{7}$を計算しなさい。
④下の図のように、半径が$9cm$、中心角が$60°$のおうぎ形$OAB$があります。
このおうぎ形の弧$AB$の長さを求めなさい。
ただし円周率は$\pi$を用いなさい。
⑤右の表は、A中学校の3年生男子80人の立ち幅とびの記録を度数分布表にまと めたものです。
度数が最も多い階級の相対度数を求めなさい。
⑥関数$y=3x$のグラフに平行で、 点$(0,2)$を通る直線の式を求めなさい。
⑦右の図の四角形$ABCD$において、点$B$と点$Dが$重なるように折ったときにできる折り目の線と
辺$AB$、$BC$との交点をそれぞれ$P,Q$とします。
2点$P,Q$を定規とコンパスを使って作図しなさい。
ただし、点を示す記号$P,Q$をかき入れ、作図に用いた線は消さないこと。
【高校受験対策/数学】死守81(問題作りました)

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#1次関数#平行と合同#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守81
①$81÷(-3)-(-11)$を計算しなさい。
②次の式を因数分解しなさい。
$(x-2)^2-18(x-2)+81$
③次の連立方程式を解きなさい。
$3x+11y=13$
$2x-3y=19$
④$311x-8y=1$を$y$について解きなさい。
⑤絶対値が$81$である数をすべて書きなさい。
⑥右の図において2直線$l,m$は平行である。
このとき、$\angle x$の大きさを求めなさい。
⑦3点$(-3,-11)$、$(2,9)$、$(k,81)$が一直線上にあるとき、 $k$の値を求めなさい。
⑧定価$8100$円のパーカーが$a$割引で売っていた。
それを買おうとレジに持っていくと、キャンペーンだったようで、そこからさらに$500$円引きしてくれた。
このとき、パーカーを買ったときの代金を$a$を使った式で表しなさい。
ただし消費税については考えないものとする。
この動画を見る
高校受験対策・死守81
①$81÷(-3)-(-11)$を計算しなさい。
②次の式を因数分解しなさい。
$(x-2)^2-18(x-2)+81$
③次の連立方程式を解きなさい。
$3x+11y=13$
$2x-3y=19$
④$311x-8y=1$を$y$について解きなさい。
⑤絶対値が$81$である数をすべて書きなさい。
⑥右の図において2直線$l,m$は平行である。
このとき、$\angle x$の大きさを求めなさい。
⑦3点$(-3,-11)$、$(2,9)$、$(k,81)$が一直線上にあるとき、 $k$の値を求めなさい。
⑧定価$8100$円のパーカーが$a$割引で売っていた。
それを買おうとレジに持っていくと、キャンペーンだったようで、そこからさらに$500$円引きしてくれた。
このとき、パーカーを買ったときの代金を$a$を使った式で表しなさい。
ただし消費税については考えないものとする。
【高校受験対策/数学】死守-80

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#2次方程式#空間図形#1次関数#確率#2次関数#文字と式#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守80
①$-3+(-4)×5$を計算しなさい。
②$4xy÷8x×6y$を計算しなさい。
③$\frac{4x-y}{2}-(2x-3y)$を計算しなさい。
④連立方程式を解きなさい。
$5x-4y=9$
$2x-3y=5$
③下の図で、$\angle x$の大きさを求めなさい。
④地球の直径は約$12700km$です。
有効数字が$1,2,7$であるとして、この距離を整数部分が1けたの数と、10の何乗かの積の形で表すと右のようになります。
アとイにあてはまる数を書きなさい。
⑦半径が$2cm$の球の体積と表面積を求めなさい。ただし円周率は$\pi$とする。
⑧赤玉3個と白玉2個が入っている袋があります。
この袋から玉を1個取り出して色を確認して、それを袋に戻してから、もう一度玉を1個取り出して色を確認します。
このとき、2回とも同じ色の玉が出る確率を求めなさい。
ただし、袋の中は見えないものとし、どの玉が出ることも同様に確からしいものとする。
⑨関数$y=ax^2$について、$x$の変域が$-2 \leqq x \leqq 3$のとき、$y$の変域は$-3b \leqq y \leqq 0$となりました。
このとき$a$の値を求めなさい。
この動画を見る
高校受験対策・死守80
①$-3+(-4)×5$を計算しなさい。
②$4xy÷8x×6y$を計算しなさい。
③$\frac{4x-y}{2}-(2x-3y)$を計算しなさい。
④連立方程式を解きなさい。
$5x-4y=9$
$2x-3y=5$
③下の図で、$\angle x$の大きさを求めなさい。
④地球の直径は約$12700km$です。
有効数字が$1,2,7$であるとして、この距離を整数部分が1けたの数と、10の何乗かの積の形で表すと右のようになります。
アとイにあてはまる数を書きなさい。
⑦半径が$2cm$の球の体積と表面積を求めなさい。ただし円周率は$\pi$とする。
⑧赤玉3個と白玉2個が入っている袋があります。
この袋から玉を1個取り出して色を確認して、それを袋に戻してから、もう一度玉を1個取り出して色を確認します。
このとき、2回とも同じ色の玉が出る確率を求めなさい。
ただし、袋の中は見えないものとし、どの玉が出ることも同様に確からしいものとする。
⑨関数$y=ax^2$について、$x$の変域が$-2 \leqq x \leqq 3$のとき、$y$の変域は$-3b \leqq y \leqq 0$となりました。
このとき$a$の値を求めなさい。
【高校受験対策/数学】関数56

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数56
Q.
図のように、円の中心$O$と点$P$が直線$l$上にあり、円の$O$半径は10$cm$、$OP$間の距離は20$cm$である。
点$O$が固定されたまま、点$P$は毎秒3$cm$の速さで直線$l$上を図の矢印の向きに進み、出発してから10秒後に停止する。
点$P$が出発してから$x$秒後の$OP$間の距離を$y cm$として次の問いに答えなさい。
①点$P$が出発してから点$O$と重なるまでの間について、$y$を$x$の式で表しなさい。
②点$P$が点$O$と重なってから停止するまでの間について、$y$を$x$の式で表しなさい。
③点$P$が出発してから停止するまでの間において、点$P$が円$O$の周上または内部にある時間は何秒間か求めなさい。
④点$P$が出来するのと同時に、毎秒1$cm$の一定の割合で円の半径が小さくなり始め、点$P$が停止するまでの間、円$O$は中心が固定されたまま徐々に小さくなっていくものとする。
点$P$が出発してから停止するまでの間において、点$P$が円$O$の周上または内部にある時間は何秒間か求めなさい。
この動画を見る
高校受験対策・関数56
Q.
図のように、円の中心$O$と点$P$が直線$l$上にあり、円の$O$半径は10$cm$、$OP$間の距離は20$cm$である。
点$O$が固定されたまま、点$P$は毎秒3$cm$の速さで直線$l$上を図の矢印の向きに進み、出発してから10秒後に停止する。
点$P$が出発してから$x$秒後の$OP$間の距離を$y cm$として次の問いに答えなさい。
①点$P$が出発してから点$O$と重なるまでの間について、$y$を$x$の式で表しなさい。
②点$P$が点$O$と重なってから停止するまでの間について、$y$を$x$の式で表しなさい。
③点$P$が出発してから停止するまでの間において、点$P$が円$O$の周上または内部にある時間は何秒間か求めなさい。
④点$P$が出来するのと同時に、毎秒1$cm$の一定の割合で円の半径が小さくなり始め、点$P$が停止するまでの間、円$O$は中心が固定されたまま徐々に小さくなっていくものとする。
点$P$が出発してから停止するまでの間において、点$P$が円$O$の周上または内部にある時間は何秒間か求めなさい。
【高校受験対策/数学】死守-78

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#比例・反比例#1次関数#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守78
①下の図のように、長方形$ABCD$の中に 1辺の長さが$\sqrt{5}cm$と$\sqrt{10}cm$の正方形がある。
このとき、斜線部分の長方形の間の長さを求めなさい。
②葉一くんは、下の図の平行四辺形$ABCD$の面積を求めるために、辺$BC$を底辺とみて、高さを測ろうと考えた。
点を$P$下の図のようにとるとき、線分$PH$が高さとなるような点$H$を作図によって求めなさい。
③1000円で、1個$a$円のクリームパン5個と1個$b$円のジャムパン3個を買うことができる。
ただし消費税は考えないものとする。
この数量の関係を表した不等式としてもっとも適切なものを、次の ア~エの中から一つ選んで、その記号を書きなさい。
ア $1000-(5a+3b) \lt 0$
イ $5a+3b \lt 1000$
ウ $1000-(5a+3b) \geqq 0$
エ $(5a+3b) \geqq 1000$
④ 右の図で、点$A$は関数$y=\frac{2}{x }$と関数$y=ax^2$のグラフの交点である。
点$B$は点$A$を$y$軸を対称の軸として対称移動させたものであり、$x$座標は$-1$である。
このことから、$a$の値はアであり、関数$y=ax^2$について、 $x$の値が1から3まで増加するときの変化の割合はイであることがわ かる。
このとき上のア・イに当てはまる数をそれぞれ書きなさい。
この動画を見る
高校受験対策・死守78
①下の図のように、長方形$ABCD$の中に 1辺の長さが$\sqrt{5}cm$と$\sqrt{10}cm$の正方形がある。
このとき、斜線部分の長方形の間の長さを求めなさい。
②葉一くんは、下の図の平行四辺形$ABCD$の面積を求めるために、辺$BC$を底辺とみて、高さを測ろうと考えた。
点を$P$下の図のようにとるとき、線分$PH$が高さとなるような点$H$を作図によって求めなさい。
③1000円で、1個$a$円のクリームパン5個と1個$b$円のジャムパン3個を買うことができる。
ただし消費税は考えないものとする。
この数量の関係を表した不等式としてもっとも適切なものを、次の ア~エの中から一つ選んで、その記号を書きなさい。
ア $1000-(5a+3b) \lt 0$
イ $5a+3b \lt 1000$
ウ $1000-(5a+3b) \geqq 0$
エ $(5a+3b) \geqq 1000$
④ 右の図で、点$A$は関数$y=\frac{2}{x }$と関数$y=ax^2$のグラフの交点である。
点$B$は点$A$を$y$軸を対称の軸として対称移動させたものであり、$x$座標は$-1$である。
このことから、$a$の値はアであり、関数$y=ax^2$について、 $x$の値が1から3まで増加するときの変化の割合はイであることがわ かる。
このとき上のア・イに当てはまる数をそれぞれ書きなさい。
【高校受験対策/数学】死守77

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守77
①$-3+(-2)$を計算しなさい。
➁$8-4÷(-2)^2$を計算しなさい。
③$5×(-5a)$を計算しなさい。
④$\frac{1}{2}x^2y÷\frac{1}{4}xy$を計算しなさい。
⑤$\sqrt{48}-\sqrt{3}$を計算しなさい。
⑥$(2a-b)^2$を展開しなさい。
⑦$x^2-x-42$を因数分解しなさい。
⑧半径が$6cm$で中心角が$45°$のおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨解が$-5,1$の2つの数となる、$x$についての2次方程式を1つ作りなさい。
⑩次のア~エのうち、数の集合と四則との関係について述べた文として正しいものをすべて選び、記号で答えなさい。
ア 自然数と自然数の加法の結果は、いつでも自然数となる。
イ 自然数と自然数の減法の結果は、いつでも整数となる。
ウ 自然数と自然数の乗法の結果は、いつでも自然数となる。
エ 自然数と自然数の除法の結果は、いつでも整数となる。
この動画を見る
高校受験対策・死守77
①$-3+(-2)$を計算しなさい。
➁$8-4÷(-2)^2$を計算しなさい。
③$5×(-5a)$を計算しなさい。
④$\frac{1}{2}x^2y÷\frac{1}{4}xy$を計算しなさい。
⑤$\sqrt{48}-\sqrt{3}$を計算しなさい。
⑥$(2a-b)^2$を展開しなさい。
⑦$x^2-x-42$を因数分解しなさい。
⑧半径が$6cm$で中心角が$45°$のおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨解が$-5,1$の2つの数となる、$x$についての2次方程式を1つ作りなさい。
⑩次のア~エのうち、数の集合と四則との関係について述べた文として正しいものをすべて選び、記号で答えなさい。
ア 自然数と自然数の加法の結果は、いつでも自然数となる。
イ 自然数と自然数の減法の結果は、いつでも整数となる。
ウ 自然数と自然数の乗法の結果は、いつでも自然数となる。
エ 自然数と自然数の除法の結果は、いつでも整数となる。
【高校受験対策/数学】死守75

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#平行と合同#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
この動画を見る
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
【中学数学】1次関数の応用~三角形の面積と2等分線~ 3-6.5【中2数学】
単元:
#数学(中学生)#中2数学#1次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
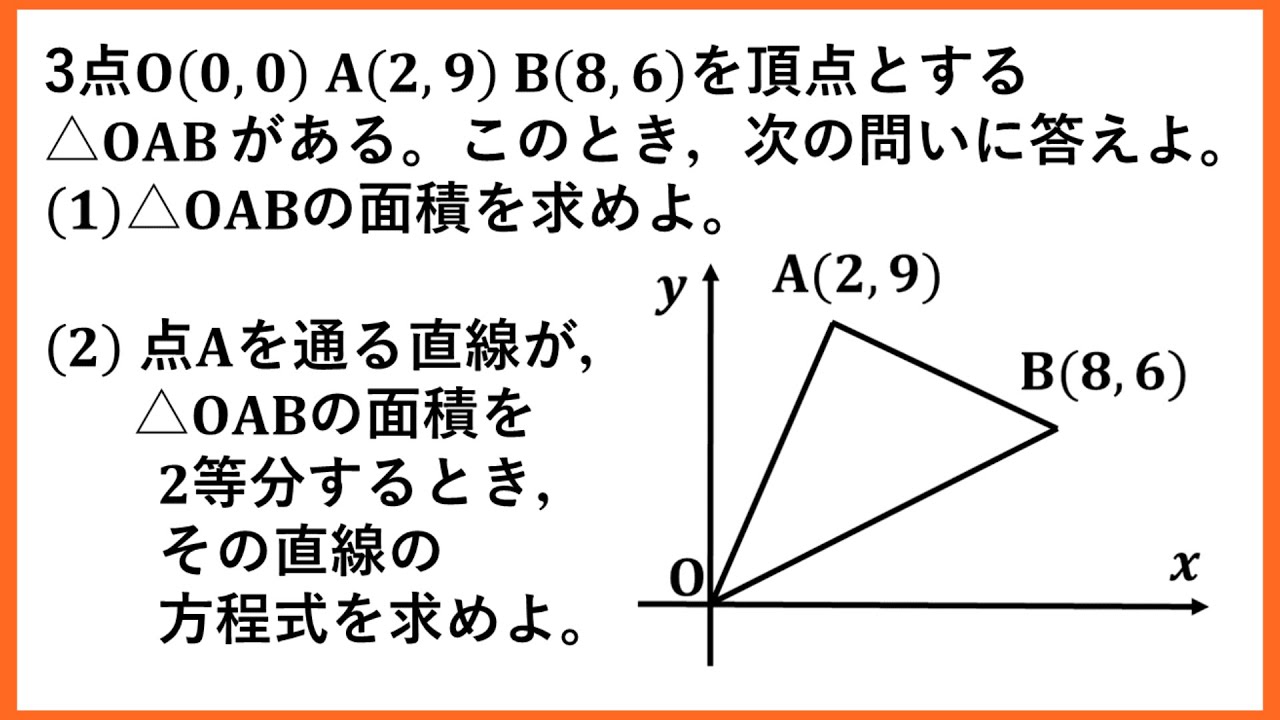
動画内の図のように3点$O(0,0)A(2,9)B(8,6)$を頂点とする$\triangle OAB$がある。
このとき、次の問いに答えよ。
1⃣
$\triangle OAB$の面積を求めよ。
2⃣
点Aを通る直線が、$\triangle OAB$の面積を2等分するとき、その直線の方程式を求めよ。
この動画を見る
動画内の図のように3点$O(0,0)A(2,9)B(8,6)$を頂点とする$\triangle OAB$がある。
このとき、次の問いに答えよ。
1⃣
$\triangle OAB$の面積を求めよ。
2⃣
点Aを通る直線が、$\triangle OAB$の面積を2等分するとき、その直線の方程式を求めよ。
【中学数学】三角形の面積を2等分する直線の問題の解き方~1次関数の応用~ 3-6【中2数学】

単元:
#中2数学#1次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)点$O$を通り、$\triangle AOB$の面積を二等分する直線の式を求めよ。
(2)点$B$を通り、$\triangle AOB$の面積を二等分する直線の式を求めよ。
この動画を見る
(1)点$O$を通り、$\triangle AOB$の面積を二等分する直線の式を求めよ。
(2)点$B$を通り、$\triangle AOB$の面積を二等分する直線の式を求めよ。
