 中2数学
中2数学
 中2数学
中2数学
【中学数学】1次関数:関数決定マスターへの道 10発目! 平行+y軸交点編

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の条件を満たす1次関数を求めよ。 直線y=2x-4に平行で、直線y=-2x+4とy軸上で交わる
この動画を見る
次の条件を満たす1次関数を求めよ。 直線y=2x-4に平行で、直線y=-2x+4とy軸上で交わる
気づけば一瞬 B
【中学数学】1次関数:関数決定マスターへの道 9発目! 2点編Ⅱ

【中学数学】1次関数:関数決定マスターへの道 8発目! 2点編Ⅰ

【一粒で2度おいしい!】確率:大阪教育大学附属高等学校平野校舎~全国入試問題解法

単元:
#数学(中学生)#確率#高校入試過去問(数学)#大阪教育大学附属高等学校平野校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 大阪教育大学附属高等学校平野校舎
さいころを2回振り
1回目の出目:a
2回目の出目:b
3つの直線 $y=ax, y=\displaystyle \frac{1}{a}x, y=b$ で囲まれる三角形を考える。
三角形ができない確率を求めなさい。
※図は動画内参照
この動画を見る
入試問題 大阪教育大学附属高等学校平野校舎
さいころを2回振り
1回目の出目:a
2回目の出目:b
3つの直線 $y=ax, y=\displaystyle \frac{1}{a}x, y=b$ で囲まれる三角形を考える。
三角形ができない確率を求めなさい。
※図は動画内参照
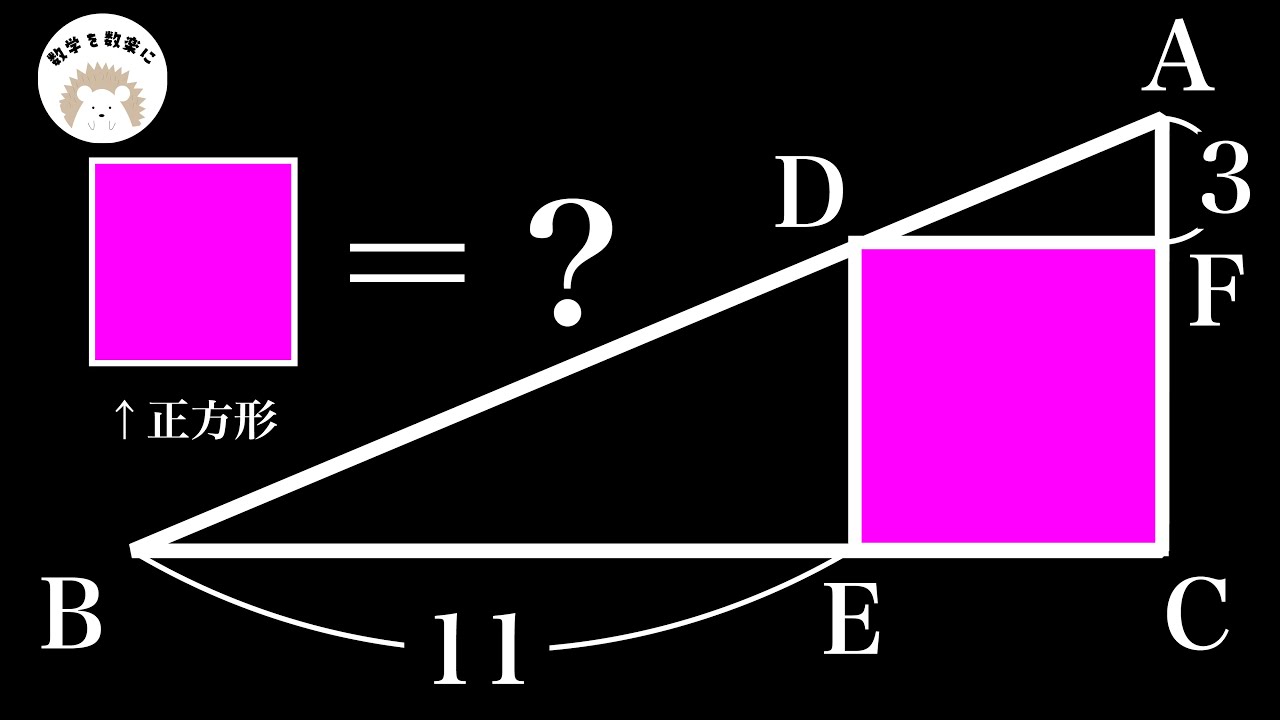
直角三角形の中の正方形
【中学数学】1次関数:関数決定マスターへの道 7発目! 平行編Ⅱ

連立方程式 求めるな! 市川高校
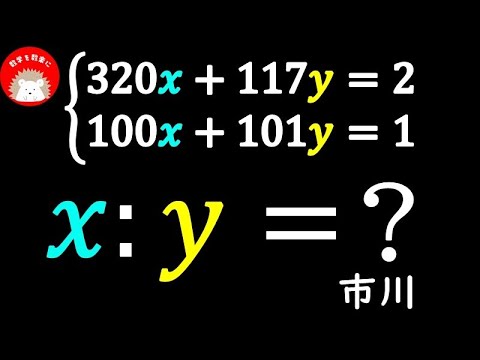
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
320x + 117y = 2 \\
100x + 101y = 1
\end{array}
\right.
\end{eqnarray}
$
のときx:y=?
市川高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
320x + 117y = 2 \\
100x + 101y = 1
\end{array}
\right.
\end{eqnarray}
$
のときx:y=?
市川高等学校
暗算できたらカッコいい

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$97^2+97 \times 6 +9=$
西武学園文理高等学校
この動画を見る
$97^2+97 \times 6 +9=$
西武学園文理高等学校
【中学数学】1次関数:関数決定マスターへの道 6発目! 平行編Ⅰ

【中学数学】1次関数:関数決定マスターへの道 5発目! 切片編

【中学数学】1次関数:関数決定マスターへの道 4発目! 変化の割合編

【中学数学】1次関数:関数決定マスターへの道 3発目! 傾き編

解き方2通り 知っていれば一瞬
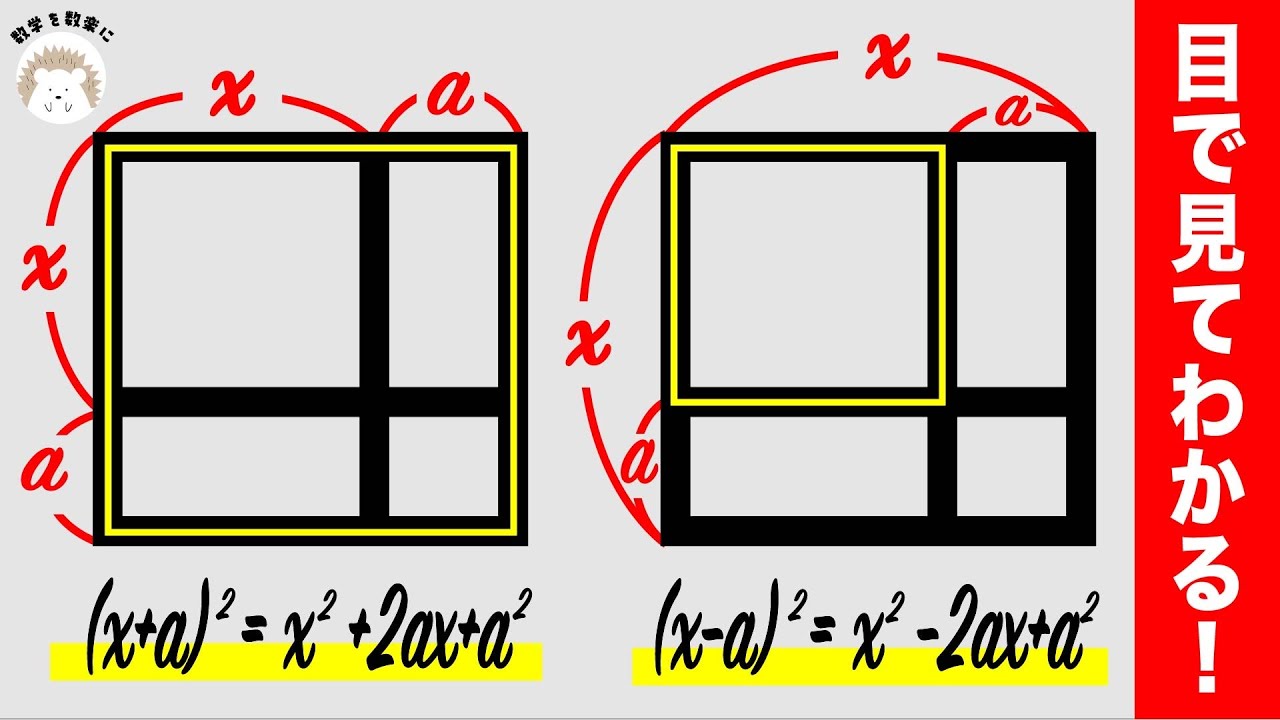
目で見てわかる乗法公式
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
$(x+a)^2 = x^2+2ax+a^2$
$(x-a)^2 = x^2-2ax+a^2$
*図は動画内参照
この動画を見る
$(x+a)^2 = x^2+2ax+a^2$
$(x-a)^2 = x^2-2ax+a^2$
*図は動画内参照
【中学数学】連立方程式:基礎の基礎から解説!その3 表で考えよう

気づけば一瞬!小学生も解ける!A
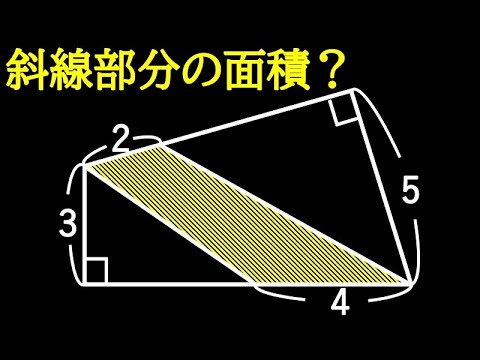
解き方2通り 気づけば一瞬!!
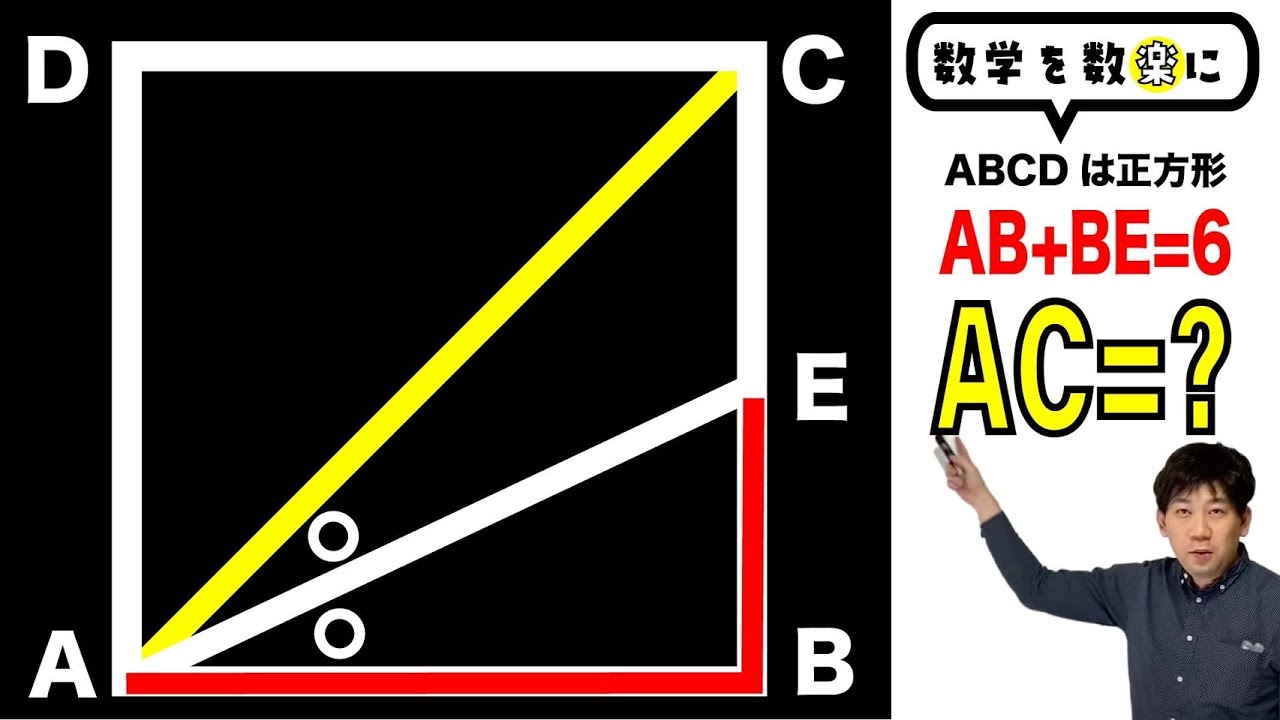
筆算する??

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$179^2+124^2-179 \times 248 -45^2$=
徳島文理高等学校
この動画を見る
$179^2+124^2-179 \times 248 -45^2$=
徳島文理高等学校
【理解深まる3分間】連立方程式:青森県高等学校~全国入試問題解法【トライ式】

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)#青森県公立高等学校#青森県高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 青森県の高等学校
グラフを利用して解を求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y = x+6 \\
x + 2y = 6
\end{array}
\right.
\end{eqnarray}$
この動画を見る
入試問題 青森県の高等学校
グラフを利用して解を求めよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y = x+6 \\
x + 2y = 6
\end{array}
\right.
\end{eqnarray}$
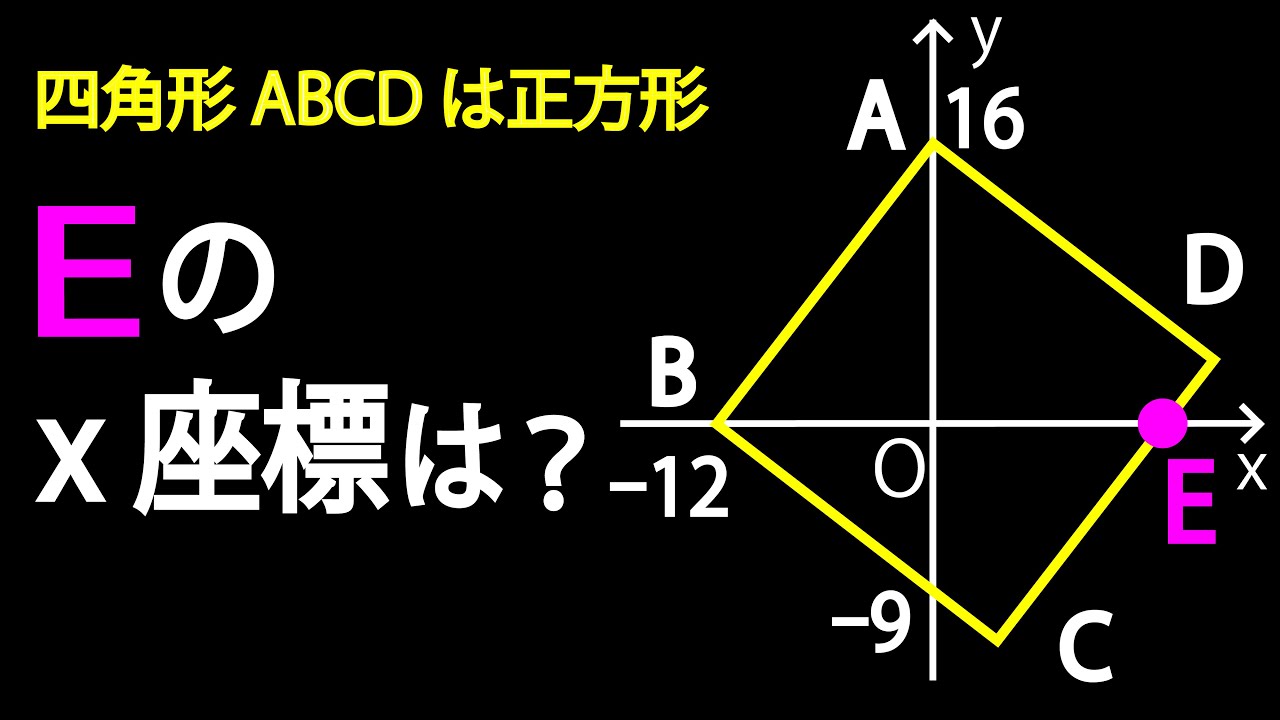
気づけば一瞬!?
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
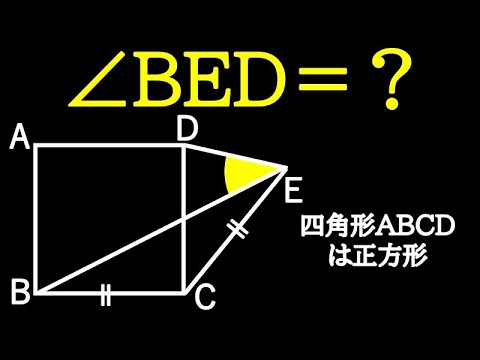
四角形ABCDは正方形
$\angle DEB = ?$
*図は動画内参照
この動画を見る
四角形ABCDは正方形
$\angle DEB = ?$
*図は動画内参照
ピタゴラスも絶賛!!解き方5通り!
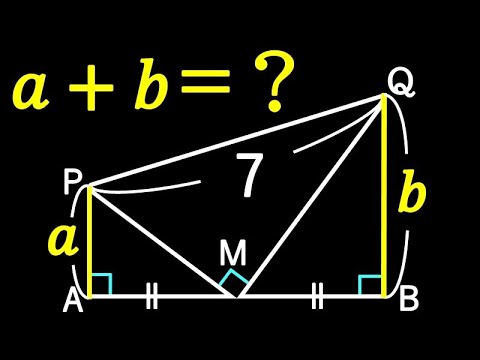
連立方程式:東京都立国立高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#東京都立国立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立国立高等学校
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{4x+y-5}{2}=x+0.25y-2 \\
4x + 3y = -6
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
この動画を見る
入試問題 東京都立国立高等学校
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{4x+y-5}{2}=x+0.25y-2 \\
4x + 3y = -6
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
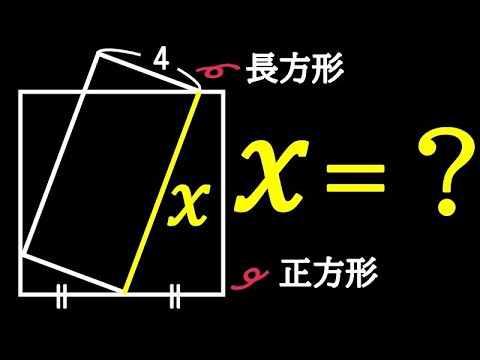
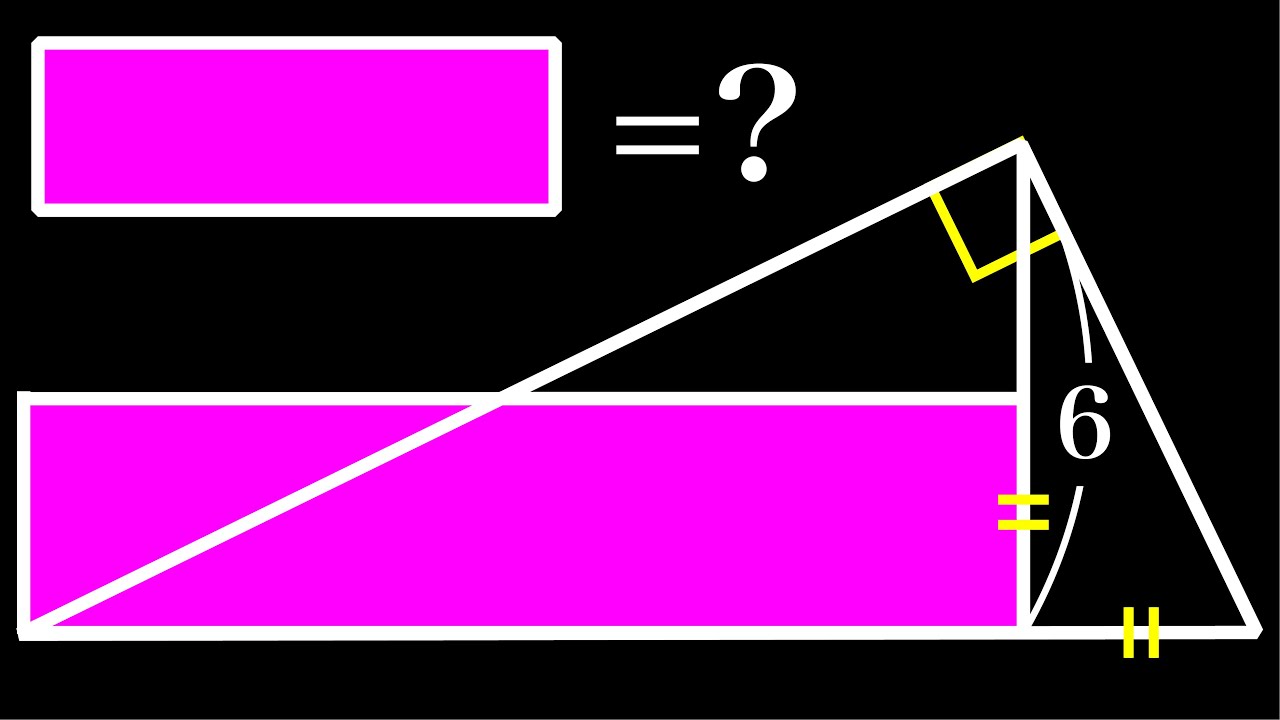
気づけば一瞬!!長方形の面積=❓
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#三角形と四角形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
長方形の面積=?
*図は動画内参照
この動画を見る
長方形の面積=?
*図は動画内参照
【中学数学】連立方程式:基礎の基礎から解説!その2 元と次って何?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
理数個別チャンネル
問題文全文(内容文):
x-y=6は何元何次方程式でしょうか?意外ときちんと習わない”元”について解説します!
この動画を見る
x-y=6は何元何次方程式でしょうか?意外ときちんと習わない”元”について解説します!
正しいものを選べ!!大阪星光学院

単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
正しいものをすべて選べ
①4辺の長さが等しい四角形をひし形という
②4つの角の大きさが等しい四角形を長方形という
③6辺の長さが等しい六角形を正六角形という
④6つの角の大きさが等しい六角形を正六角形という
大阪星光学院高等学校
この動画を見る
正しいものをすべて選べ
①4辺の長さが等しい四角形をひし形という
②4つの角の大きさが等しい四角形を長方形という
③6辺の長さが等しい六角形を正六角形という
④6つの角の大きさが等しい六角形を正六角形という
大阪星光学院高等学校
単純そうで少し難しい B
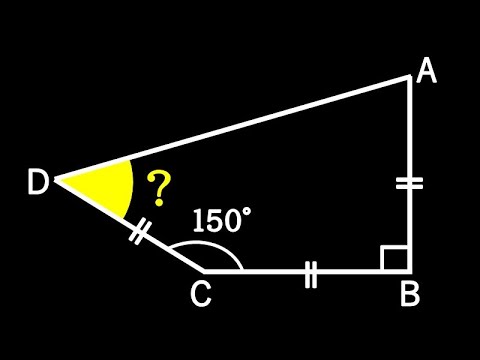
【中学数学】連立方程式:基礎の基礎から解説!その1 連立方程式って?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x+y=10,x-y=6$を同時に満たす整数解を考えながら連立方程式を学んでいこう。
この動画を見る
$x+y=10,x-y=6$を同時に満たす整数解を考えながら連立方程式を学んでいこう。
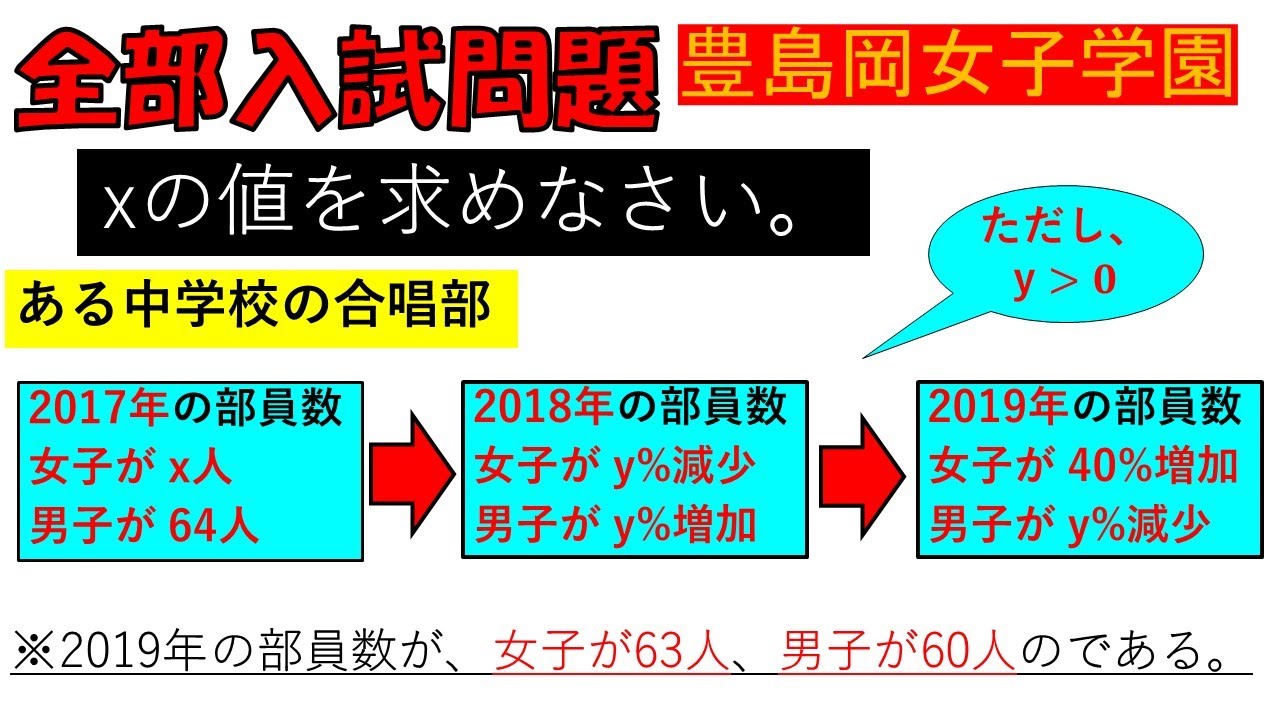
連立方程式:豊島岡女子学園高等学校~全国入試問題解法【神授業】
単元:
#数学(中学生)#中1数学#中2数学#方程式#連立方程式#高校入試過去問(数学)#豊島岡女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 豊島岡女子学園高等学校
ある中学校の合唱部の2017年の部員数は、女子が$x$ 人、男子が64人でした。2018年の部員数は、2017 年と比べて女子が$y$%減り、男子が$y$%増えました。 2019年の部員数は、2018年と比べて女子が40%増 え、男子が$y$%減りました。
2019年の部員数が、女子が63人、男子が60人のとき
$x$の値を求めなさい。
(ただし、$ y\gt 0$)
この動画を見る
入試問題 豊島岡女子学園高等学校
ある中学校の合唱部の2017年の部員数は、女子が$x$ 人、男子が64人でした。2018年の部員数は、2017 年と比べて女子が$y$%減り、男子が$y$%増えました。 2019年の部員数は、2018年と比べて女子が40%増 え、男子が$y$%減りました。
2019年の部員数が、女子が63人、男子が60人のとき
$x$の値を求めなさい。
(ただし、$ y\gt 0$)
京都女子
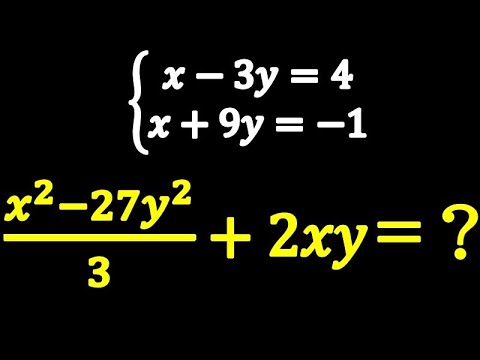
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x - 3y = 4 \\
x + 9y = -1
\end{array}
\right.
\end{eqnarray}
$
のとき
$\frac{x^2-27y^2}{3}+2xy$
京都女子高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x - 3y = 4 \\
x + 9y = -1
\end{array}
\right.
\end{eqnarray}
$
のとき
$\frac{x^2-27y^2}{3}+2xy$
京都女子高等学校
