 中2数学
中2数学
 中2数学
中2数学
親子丼が親子になる確率は?

【中学数学】三角形と比~分かりやすく丁寧に証明~ 5-3【中3数学】

単元:
#数学(中学生)#中2数学#平行と合同
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
DE//BCならば
AD:AB=AE:AC=DE:BC
AD:DB=AE:EC
を証明します
この動画を見る
DE//BCならば
AD:AB=AE:AC=DE:BC
AD:DB=AE:EC
を証明します
【中学数学】数学用語チェック絵本 中2の用語”せめて”これだけは覚えよう!!act2まとめ

単元:
#数学(中学生)#中1数学#中2数学#式の計算(単項式・多項式・式の四則計算)#連立方程式#資料の活用#1次関数#平行と合同#確率#三角形と四角形
指導講師:
理数個別チャンネル
問題文全文(内容文):
中2で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!act2vol.1~7の方も見てね♪
この動画を見る
中2で登場する数学用語の中で、せめてこれだけは覚えてほしいものをピックアップ!act2vol.1~7の方も見てね♪
【未知なるものは…!】文章題:明治学院高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#明治学院高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
所持金で$ \color{red}{プリンを8個}$買うと$ \color{red}{220円}$余り,$ \color{red}{10個}$買うと合計金額から$ \color{blue}{1割引き}$になるので$ \color{red}{60円}$余る.
このときの$ \color{red}{所持金}$はいくらか?
明治学院高校過去問
この動画を見る
所持金で$ \color{red}{プリンを8個}$買うと$ \color{red}{220円}$余り,$ \color{red}{10個}$買うと合計金額から$ \color{blue}{1割引き}$になるので$ \color{red}{60円}$余る.
このときの$ \color{red}{所持金}$はいくらか?
明治学院高校過去問
これどれくらいすごいん?
単元:
#数学(中学生)#中2数学#数A#場合の数と確率#確率#確率#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
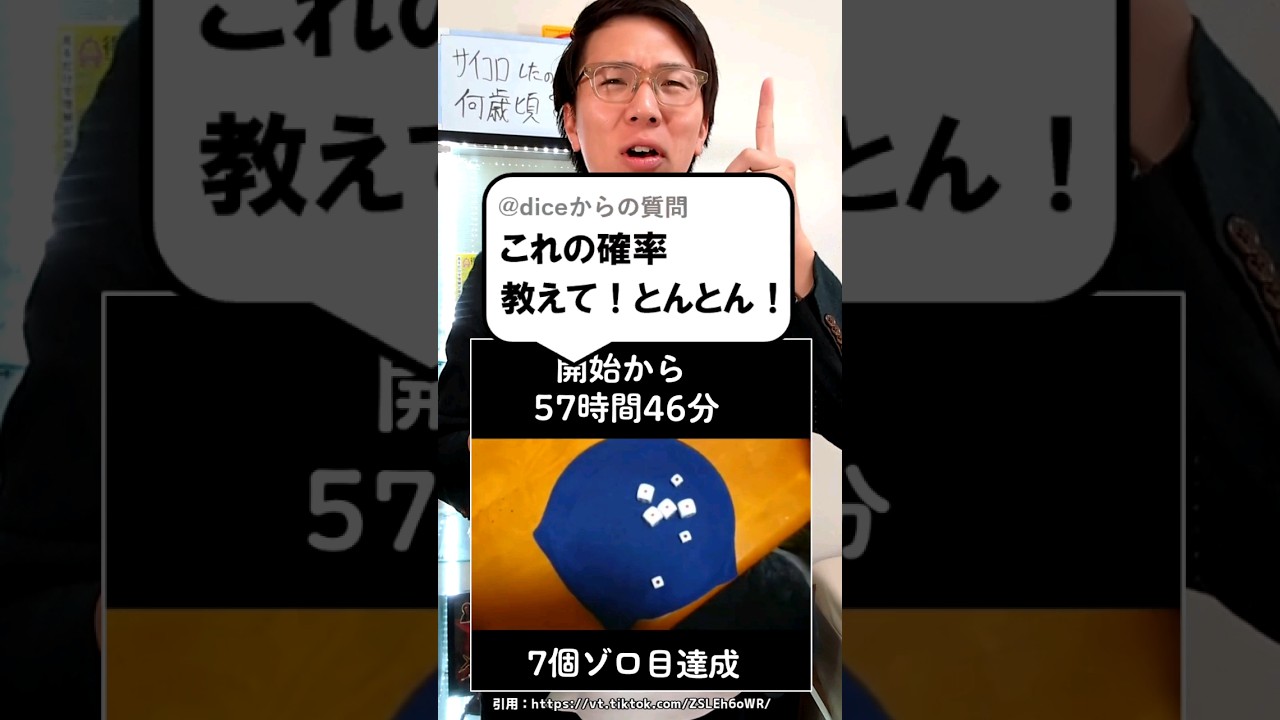
問題文全文(内容文):
7つのサイコロがゾロ目になる確率を計算
この動画を見る
7つのサイコロがゾロ目になる確率を計算
気付けば気持ちいい!!連立方程式 慶應義塾

単元:
#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 6 \\
6xy = 5
\end{array}
\right.
\end{eqnarray}
慶應義塾高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 6 \\
6xy = 5
\end{array}
\right.
\end{eqnarray}
慶應義塾高等学校
1次関数の基礎を60秒で

【挑戦しよう!】連立方程式:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x \gt y $において,
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y+xy^2-9xy=120 \\
xy+x+y-9=-22
\end{array}
\right.
\end{eqnarray}$
の解は$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\Box \\
y=\Box
\end{array}
\right.
\end{eqnarray}$ または,$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\Box \\
y=\Box
\end{array}
\right.
\end{eqnarray}$
慶應義塾高校過去問
この動画を見る
$ x \gt y $において,
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y+xy^2-9xy=120 \\
xy+x+y-9=-22
\end{array}
\right.
\end{eqnarray}$
の解は$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\Box \\
y=\Box
\end{array}
\right.
\end{eqnarray}$ または,$\begin{eqnarray}
\left\{
\begin{array}{l}
x=\Box \\
y=\Box
\end{array}
\right.
\end{eqnarray}$
慶應義塾高校過去問
【ひるまず進め!】計算:法政大学高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)#法政大学高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \left(1.2\div 0.375+\dfrac{-2^3}{3}\times 4.2\right)\div \left(-\dfrac{2}{3}\right)^3$を計算しなさい.
法政大高校過去問
この動画を見る
$ \left(1.2\div 0.375+\dfrac{-2^3}{3}\times 4.2\right)\div \left(-\dfrac{2}{3}\right)^3$を計算しなさい.
法政大高校過去問
ラーメンはどれくらい伸びるのか?

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
中国4000年間ずっとラーメン放置してたらどれくらい伸びるのか計算します.
この動画を見る
中国4000年間ずっとラーメン放置してたらどれくらい伸びるのか計算します.
中国4000年ラーメンが伸び続けたら何km?

慶應入って優勝する確率は?

【「公式」はあるけれど…!】島根県:一次関数~全国入試問題解法

単元:
#数学(中学生)#中2数学#1次関数#三角形と四角形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2点 $ A(1,2),B(3,5)$の間の距離を求めなさい.
島根県入試問題過去問
この動画を見る
2点 $ A(1,2),B(3,5)$の間の距離を求めなさい.
島根県入試問題過去問
これも連立方程式だって分かってる!?~全国入試問題解法 #shorts #数学 #math #高校受験
単元:
#数学(中学生)#中2数学#中3数学#連立方程式#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
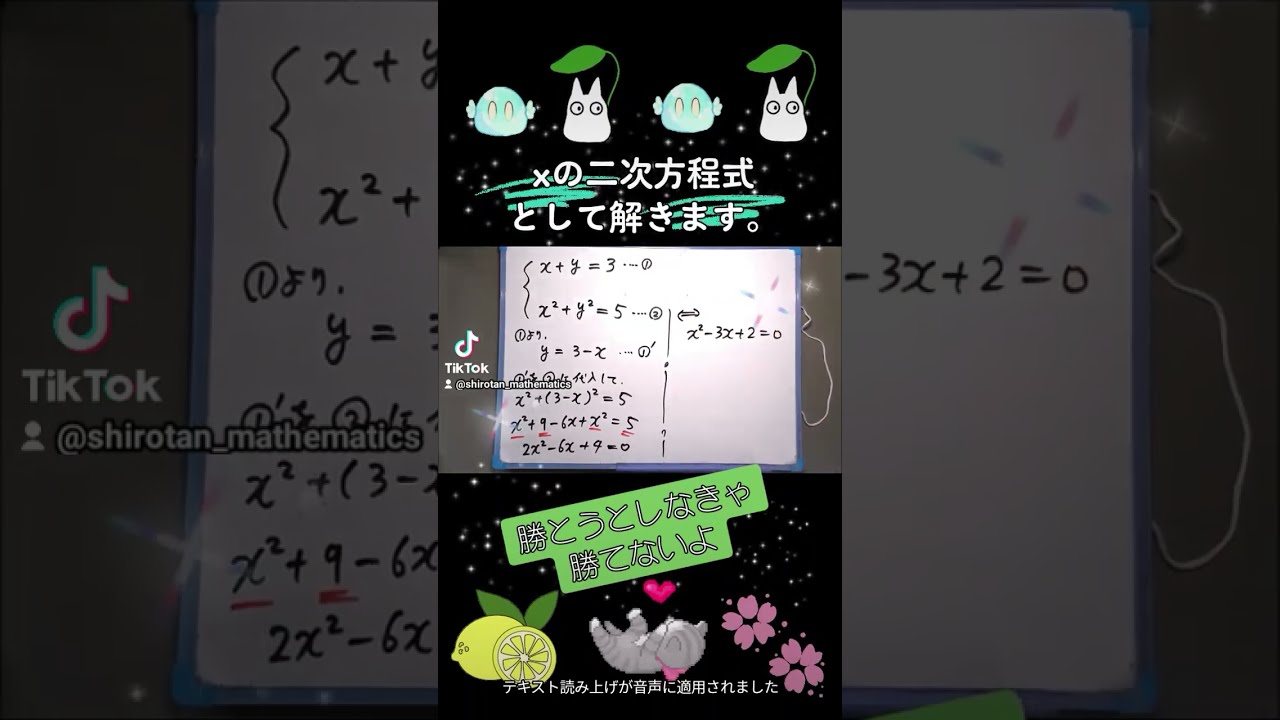
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x + y = 3 \\
x^2+y^2=5
\end{array}
\right.
\end{eqnarray}$ を解け.
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x + y = 3 \\
x^2+y^2=5
\end{array}
\right.
\end{eqnarray}$ を解け.
【基礎と応用のどちらが良いか!】一次関数:和洋国府台女子高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#和洋国府台女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
直線$ y=ax+8 $が2点$ (-2,b),(5,18)$を通るとき$ a,b $の値を求めよ.
和洋国府台女子高校過去問
この動画を見る
直線$ y=ax+8 $が2点$ (-2,b),(5,18)$を通るとき$ a,b $の値を求めよ.
和洋国府台女子高校過去問
【ルールを抑えるのが大切!】文字式:福岡大学附属大濠高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \left(\dfrac{2x+5y}{3}-\dfrac{x+7y}{6}\right)\div \dfrac{xy}{2}$を計算し,簡単にすると$ \Box $である.
福岡大学附属大濠高等学校過去問
この動画を見る
$ \left(\dfrac{2x+5y}{3}-\dfrac{x+7y}{6}\right)\div \dfrac{xy}{2}$を計算し,簡単にすると$ \Box $である.
福岡大学附属大濠高等学校過去問
連立方程式にも上手い解き方はある15秒~全国入試問題解法 #shorts #数学 #入試対策 #math #動体視力

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連立方程式にも上手い解き方はある15秒~全国入試問題解法 #shorts #数学 #入試対策 #math #動体視力
この動画を見る
連立方程式にも上手い解き方はある15秒~全国入試問題解法 #shorts #数学 #入試対策 #math #動体視力
手強いぞ 連立方程式 慶應義塾(神奈川)

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け(x>y)
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y + xy^2 -9xy = 120 \\
xy + x + y - 9 = -22
\end{array}
\right.
\end{eqnarray}
2023慶應義塾高等学校(改)
この動画を見る
連立方程式を解け(x>y)
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2y + xy^2 -9xy = 120 \\
xy + x + y - 9 = -22
\end{array}
\right.
\end{eqnarray}
2023慶應義塾高等学校(改)
【まずは解くこと…!】文字式:明治大学付属明治高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#平方根#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\sqrt2x+\sqrt7y=3 \\
\sqrt7x-\sqrt2y=-6
\end{array}
\right.
\end{eqnarray}$
のとき,$ y-x=\Box $
明治大学付属明治高等学校過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
\sqrt2x+\sqrt7y=3 \\
\sqrt7x-\sqrt2y=-6
\end{array}
\right.
\end{eqnarray}$
のとき,$ y-x=\Box $
明治大学付属明治高等学校過去問
連立方程式
単元:
#連立方程式#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y,z$は実数とする.これを解け.
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy+x+y=1 \\
x^2y^2+x^2+y^2=31
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$x,y,z$は実数とする.これを解け.
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy+x+y=1 \\
x^2y^2+x^2+y^2=31
\end{array}
\right.
\end{eqnarray}$
計算したらどれが1番大きいの? おかやま山陽(岡山)

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
数学を数楽に
問題文全文(内容文):
1番大きいのは?
(1)71×79
(2)72×78
(3)73×77
(4)74×76
(5)75×75
おかやま山陽高校
この動画を見る
1番大きいのは?
(1)71×79
(2)72×78
(3)73×77
(4)74×76
(5)75×75
おかやま山陽高校
【2つの解き方!】確率:東京都公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#東京都公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
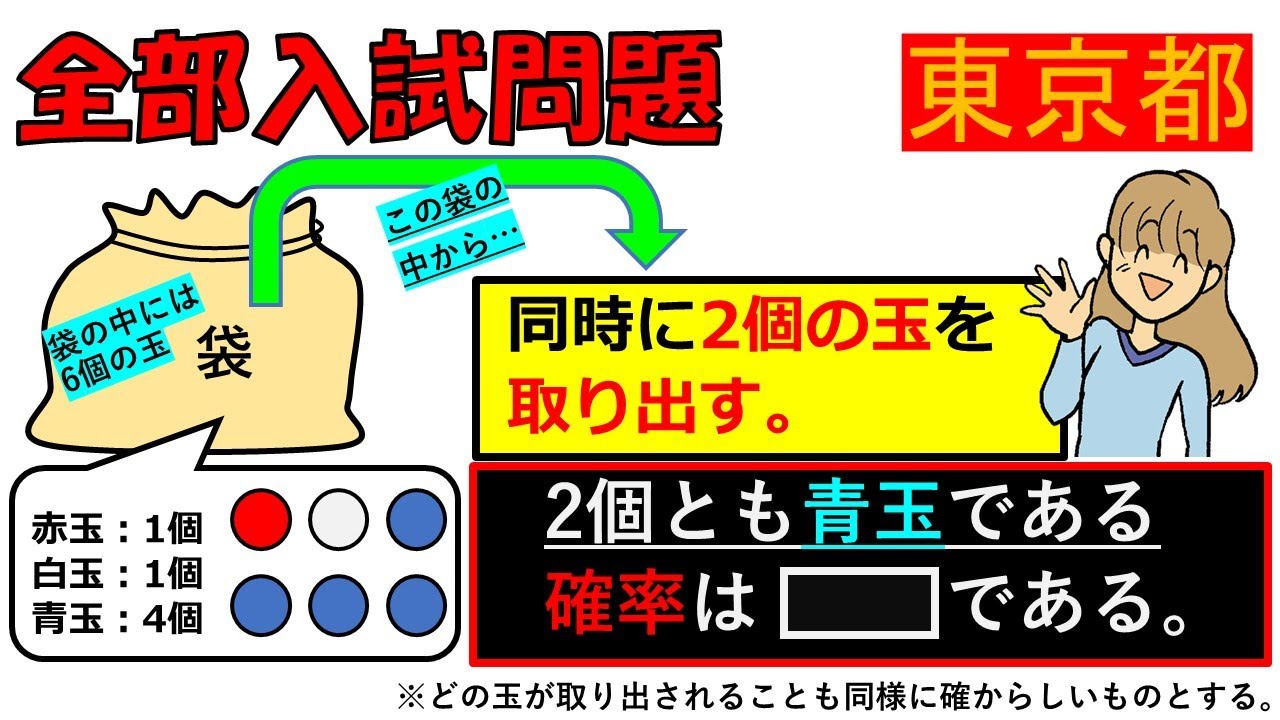
問題文全文(内容文):
袋の中には赤玉1個,白玉1個,青玉4個の合計6個の玉が入っている.
この袋の中には同時に2個の玉を取り出す.
2個とも青玉である確率を求めよ.
※どの玉が取り出されることも同様に確からしいものとする.
東京都公立高等学校
この動画を見る
袋の中には赤玉1個,白玉1個,青玉4個の合計6個の玉が入っている.
この袋の中には同時に2個の玉を取り出す.
2個とも青玉である確率を求めよ.
※どの玉が取り出されることも同様に確からしいものとする.
東京都公立高等学校
【道具を使いこなせ!】連立方程式:東京都公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#東京都公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+3y=1 \\
8x+9y=7
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け.
東京都公立高等学校過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+3y=1 \\
8x+9y=7
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け.
東京都公立高等学校過去問
暗算で解ける? 高知中央

数学の問題を解くのに作図は大切だという15秒間~全国入試問題解法 #shorts #数学 #高校入試 #math #動体視力

単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
1次関数$ y=ax+3(a \lt 0)$
$ -2 \leqq x \leqq 5 $であるとき,$ -2 \leqq y \leqq b $となるような
$ a $と$ b $の値を求めなさい.
函館ラサール高校過去問
この動画を見る
1次関数$ y=ax+3(a \lt 0)$
$ -2 \leqq x \leqq 5 $であるとき,$ -2 \leqq y \leqq b $となるような
$ a $と$ b $の値を求めなさい.
函館ラサール高校過去問
地面掘るだけで20兆円貰える確率

中学2年生問題 ただの連立方程式

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
2021x+2022y=2023 \\
4045x+4043y=4046
\end{array}
\right.
\end{eqnarray}$
これを解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2021x+2022y=2023 \\
4045x+4043y=4046
\end{array}
\right.
\end{eqnarray}$
これを解け.
解けるように作られた連立方程式

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数$x,y,z$を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+2y+3z)^2=14(x^2+y^2+z^2) \\
x+y+z=18
\end{array}
\right.
\end{eqnarray}$
この動画を見る
実数$x,y,z$を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+2y+3z)^2=14(x^2+y^2+z^2) \\
x+y+z=18
\end{array}
\right.
\end{eqnarray}$
【比の計算ならば…!】連立方程式:広島大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#広島大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x:(2y+13)=3:1\\
5x+6y=3
\end{array}
\right.
\end{eqnarray}$
広大附属高校過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x:(2y+13)=3:1\\
5x+6y=3
\end{array}
\right.
\end{eqnarray}$
広大附属高校過去問
123456789✖️9➕10🟰?

