 平方根
平方根
 平方根
平方根
【一度は経験したい!】文字式:お茶の水女子大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)#お茶の水女子大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
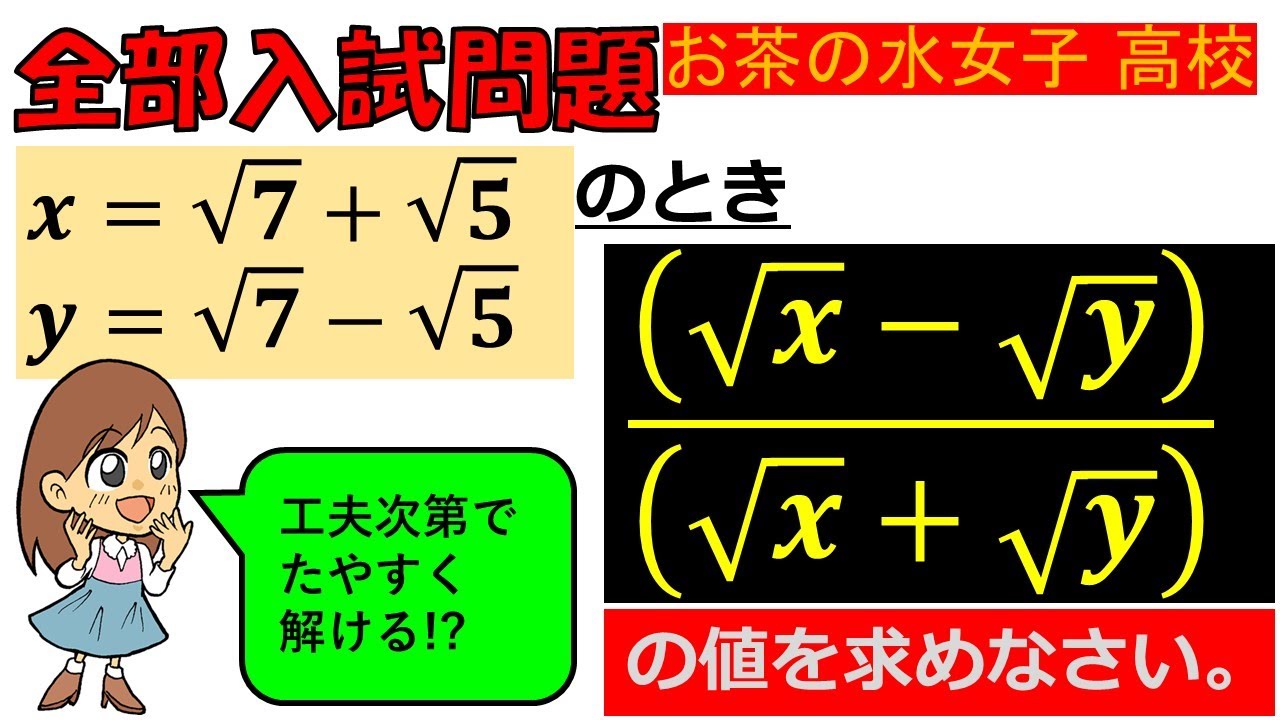
$ x=\sqrt7+\sqrt5 $
$ y=\sqrt7-\sqrt5 $ のとき,$ \dfrac{(\sqrt x-\sqrt y)}{(\sqrt x+\sqrt y)}$の値を求めなさい.
お茶の水女子高校過去問
この動画を見る
$ x=\sqrt7+\sqrt5 $
$ y=\sqrt7-\sqrt5 $ のとき,$ \dfrac{(\sqrt x-\sqrt y)}{(\sqrt x+\sqrt y)}$の値を求めなさい.
お茶の水女子高校過去問
【冷静に考えて!】平方根:灘高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#灘高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
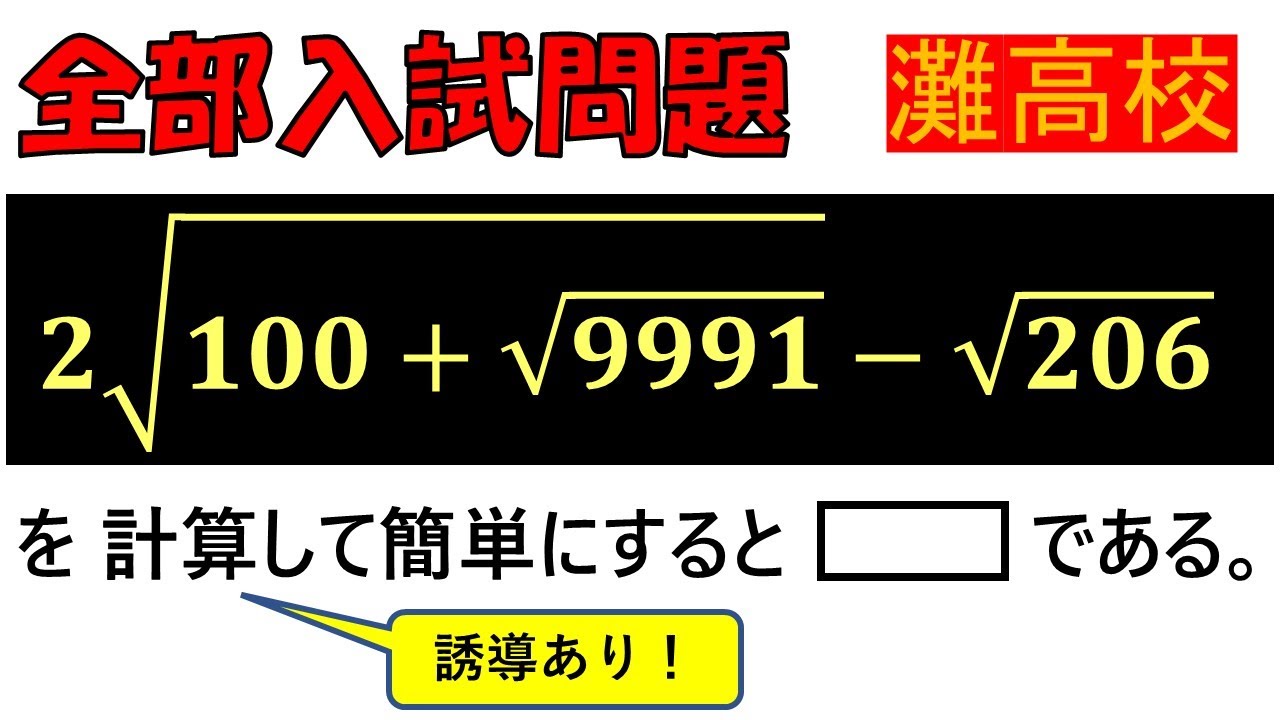
$ 2\sqrt{100+\sqrt{9991}}-\sqrt{206}$を計算して簡単にすると$ \Box $である.
灘高校過去問
この動画を見る
$ 2\sqrt{100+\sqrt{9991}}-\sqrt{206}$を計算して簡単にすると$ \Box $である.
灘高校過去問
【一度は経験したい!】平方根:沖縄県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#沖縄県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt5 \leqq n \leqq \sqrt{11}$となるような自然数$ n $の値は$ n =\Box $である.
沖縄県公立高等学校過去問
この動画を見る
$ \sqrt5 \leqq n \leqq \sqrt{11}$となるような自然数$ n $の値は$ n =\Box $である.
沖縄県公立高等学校過去問
【迷うなら手を動かせ!】平方根:東京都立立川高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立立川高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{(\sqrt{11}-\sqrt3)(\sqrt6+\sqrt{22})}{2\sqrt2}+\dfrac{(\sqrt6-3\sqrt2)^2}{3}$の値を求めよ.
都立立川高校過去問
この動画を見る
$ \dfrac{(\sqrt{11}-\sqrt3)(\sqrt6+\sqrt{22})}{2\sqrt2}+\dfrac{(\sqrt6-3\sqrt2)^2}{3}$の値を求めよ.
都立立川高校過去問
【「知ってるカタチ」を見つけたら…!】平方根:福井県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
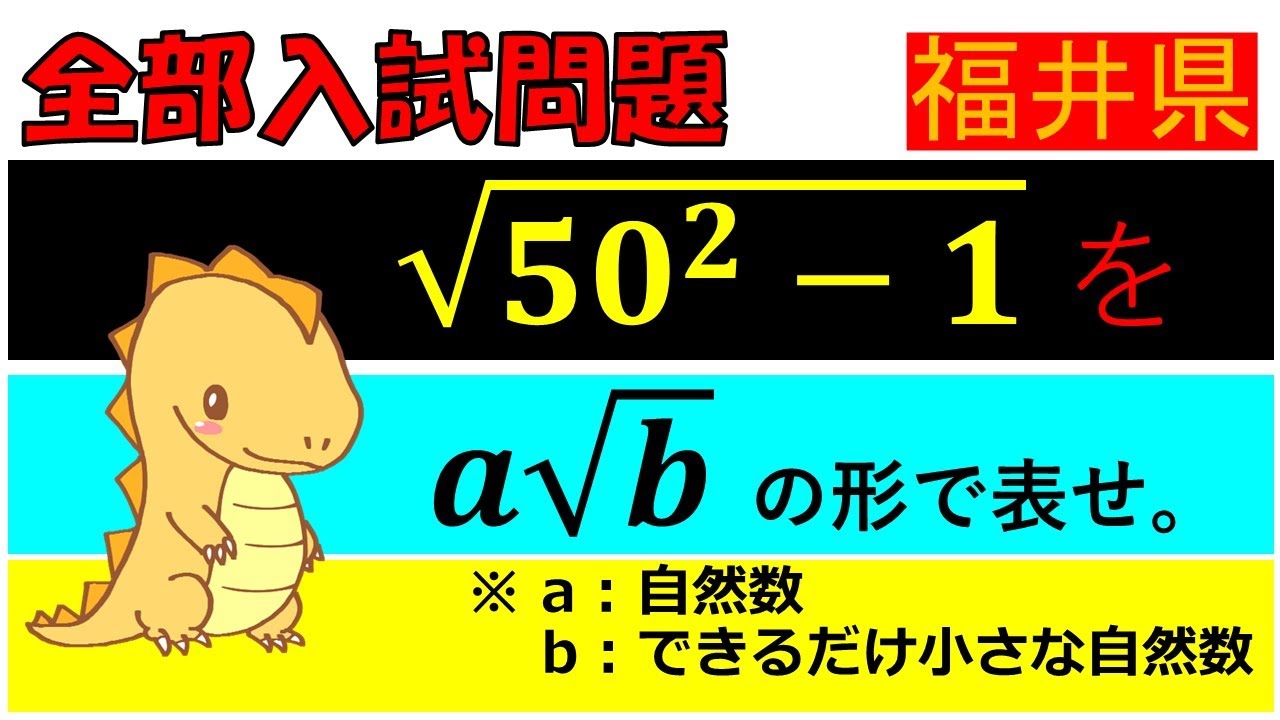
$ \sqrt{50^2-1}$を$ a\sqrt b$の形で表せ.
※a:自然数,b;できるだけ小さな自然数
福井県公立高等学校過去問
この動画を見る
$ \sqrt{50^2-1}$を$ a\sqrt b$の形で表せ.
※a:自然数,b;できるだけ小さな自然数
福井県公立高等学校過去問
【流れをつかめば必ず解ける!】平方根:東海高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東海高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
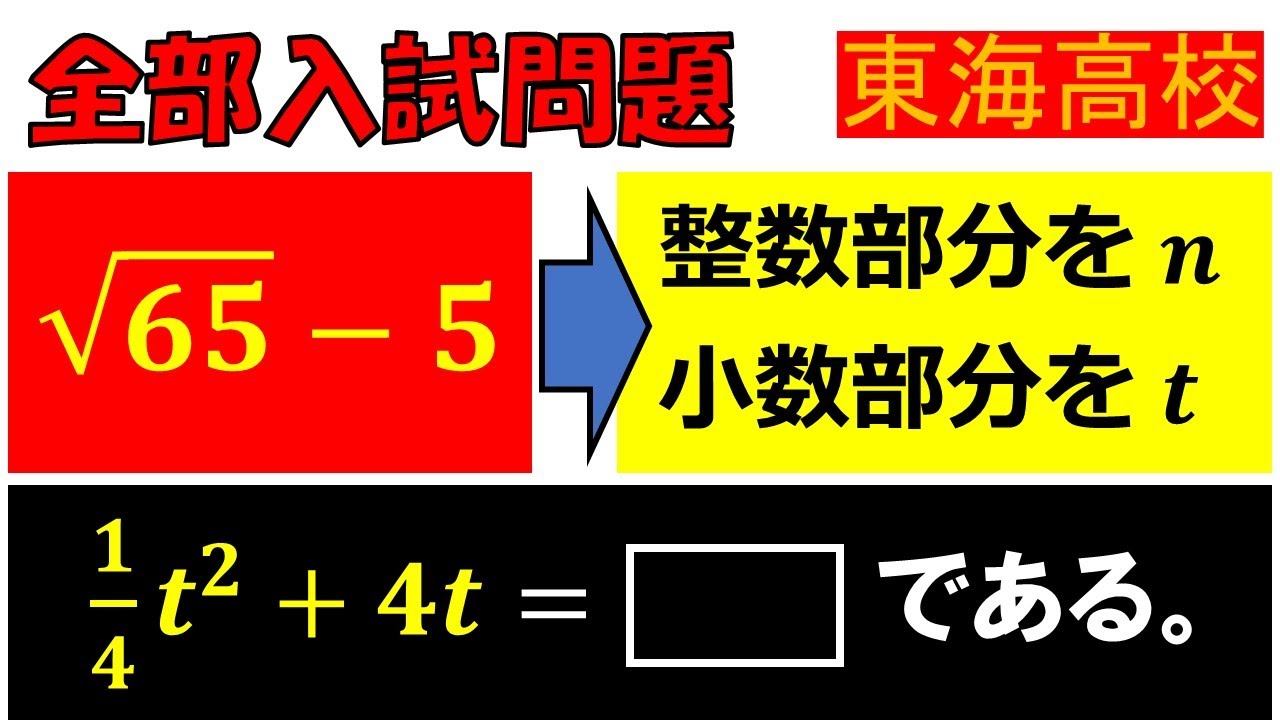
$ \sqrt{65}-5 $の整数部分を$ n $とし,小数部分を$ t $とする.
$ \dfrac{1}{4}t^2+4t=\Box $である.
東海高校過去問
この動画を見る
$ \sqrt{65}-5 $の整数部分を$ n $とし,小数部分を$ t $とする.
$ \dfrac{1}{4}t^2+4t=\Box $である.
東海高校過去問
【計算の順序を考えよう!】平方根:早稲田大学系属早稲田実業学校高等部~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (\sqrt5-\sqrt3+\sqrt2)^2 \times(\sqrt5+\sqrt3-\sqrt2)^2$を計算せよ.
早稲田実業高等部過去問
この動画を見る
$ (\sqrt5-\sqrt3+\sqrt2)^2 \times(\sqrt5+\sqrt3-\sqrt2)^2$を計算せよ.
早稲田実業高等部過去問
【爆速でやり方をマスター!!】平方根①(平方根とは何か、乗法と徐法)〔現役講師解説、中学、数学〕

単元:
#数学(中学生)#中3数学#平方根
指導講師:
3rd School
問題文全文(内容文):
中学3年生 数学
平方根(乗法と除法)
Q.次の平方根は?
①4 ②0.01 ③2
①$\sqrt{2}\times\sqrt{3}$ ②$\sqrt{3}\times\sqrt{7}$ ③$\sqrt{6}\div\sqrt{2}$ ④$\sqrt{45}\div\sqrt{5}$
Q.根号の中をできるだけ簡単にしなさい。
①$\sqrt{20}$ ②$\sqrt{48}$
この動画を見る
中学3年生 数学
平方根(乗法と除法)
Q.次の平方根は?
①4 ②0.01 ③2
①$\sqrt{2}\times\sqrt{3}$ ②$\sqrt{3}\times\sqrt{7}$ ③$\sqrt{6}\div\sqrt{2}$ ④$\sqrt{45}\div\sqrt{5}$
Q.根号の中をできるだけ簡単にしなさい。
①$\sqrt{20}$ ②$\sqrt{48}$
【まず自力で解こう!】文字式:成城学園高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#中3数学#平方根#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x=2\sqrt3+2\sqrt2 $
$ y=\sqrt3-\sqrt2 $
のとき,$ x^2-4y^2 $の値を求めよ.
成蹊学園高校過去問
この動画を見る
$ x=2\sqrt3+2\sqrt2 $
$ y=\sqrt3-\sqrt2 $
のとき,$ x^2-4y^2 $の値を求めよ.
成蹊学園高校過去問
【解法を決めるのはキミ自身だ】文字式:関西大倉高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#中3数学#方程式#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x=4-\sqrt{2022}$のとき,$ x^2-8x+15 $の値を求めよ.
関西大倉高等学校過去問
この動画を見る
$ x=4-\sqrt{2022}$のとき,$ x^2-8x+15 $の値を求めよ.
関西大倉高等学校過去問
【計算のルールと平方根のガイネン】平方根:東京都立新宿高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{\sqrt{(-3)^2}+(-2)^2}{(-\sqrt2)^3}+\dfrac{(\sqrt3-2)^2}{\sqrt{2^3}}$を計算せよ.
都立新宿高校過去問
この動画を見る
$ \dfrac{\sqrt{(-3)^2}+(-2)^2}{(-\sqrt2)^3}+\dfrac{(\sqrt3-2)^2}{\sqrt{2^3}}$を計算せよ.
都立新宿高校過去問
複雑に見える計算問題をスッキリと解く動画~全国入試問題解法 #shorts #数学 #高校受験 #sound

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right)^2+\left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right)\left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)-\left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)^2 $を計算せよ.
都立国立高校過去問
この動画を見る
$ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right)^2+\left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right)\left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)-\left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)^2 $を計算せよ.
都立国立高校過去問
【今後増える傾向 !?】整数:大阪教育大学附属高等学校池田校舎~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
18の正の約数の平方根のうち,すべての正の数の和は
$ (1+\sqrt2)x $
という式で表される.
$ x $の値を求めなさい.
大教大高校池田過去問
この動画を見る
18の正の約数の平方根のうち,すべての正の数の和は
$ (1+\sqrt2)x $
という式で表される.
$ x $の値を求めなさい.
大教大高校池田過去問
大阪大 無理数の無理数乗=有理数

単元:
#数学(中学生)#中3数学#平方根
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$\log_3 4$は無理数であることを証明せよ.
(2)a,bは無理数で$a^b$が有理数であるような数の組a,bを求めよ.
大阪大過去問
この動画を見る
(1)$\log_3 4$は無理数であることを証明せよ.
(2)a,bは無理数で$a^b$が有理数であるような数の組a,bを求めよ.
大阪大過去問
高等学校入学試験予想問題:洛南高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#空間図形#1次関数#2次関数#平面図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ \left(4-\dfrac{7}{3}\right)\times \left(-\dfrac{3}{5}+\dfrac{1}{2}\right)$を計算せよ.
(2)$ \ell:y=(a+2)x+b-1$
$ m:y=bx-a^2 $について,
$ a=\sqrt2,b=1$のとき,$ \ell,m$の交点は?
(3)$ a=\sqrt5-\sqrt3,b=\sqrt5+\sqrt3 $のとき,$ a^2-ab-b^2$の値は?
$ \boxed{2}$
図のように,2点$ A,B $が$ y-ax^2 $のグラフ上にあり,$ A $の座標は$ (3,27)$,$B$のx座標は-2である.
3点$ C,D,E $は直線$ OA $上,$ \triangle OBC,\triangle BCF,\triangle CFD,\triangle FDG,
\triangle DGE,\triangle GEA $の面積はすべて等しい.
このとき,次の問いに答えよ.
(1)点$ B$のy座標を求めよ.
(2)点$ C $の座標を求めよ.
(3)直線$ EG $の傾きを求めよ.
$ \boxed{3}$
図のように,底面の半径が3cm,母線の長さが5cmの円錐の中に半径の等しい2つの球$ P,Q $があります.
2つの球$ P,Q $は互いに接し,円錐の底面と側面に接しているとき,次の問いに答えなさい.
ただし,2つの球の中心と,円錐の頂点と,円錐の底面の中心は同じ平面上にあるものとする.
(1)球$ P$の半径を求めよ.
(2)円錐の体積は,$ P $の体積の何倍か.
(3)球$ P $と円錐の側面が接する点を$ A $とする.
点$ A $を通り,円錐の底面に平行な平面で球$ P $を切断するとき,球$ P $の切断面の面積を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ \left(4-\dfrac{7}{3}\right)\times \left(-\dfrac{3}{5}+\dfrac{1}{2}\right)$を計算せよ.
(2)$ \ell:y=(a+2)x+b-1$
$ m:y=bx-a^2 $について,
$ a=\sqrt2,b=1$のとき,$ \ell,m$の交点は?
(3)$ a=\sqrt5-\sqrt3,b=\sqrt5+\sqrt3 $のとき,$ a^2-ab-b^2$の値は?
$ \boxed{2}$
図のように,2点$ A,B $が$ y-ax^2 $のグラフ上にあり,$ A $の座標は$ (3,27)$,$B$のx座標は-2である.
3点$ C,D,E $は直線$ OA $上,$ \triangle OBC,\triangle BCF,\triangle CFD,\triangle FDG,
\triangle DGE,\triangle GEA $の面積はすべて等しい.
このとき,次の問いに答えよ.
(1)点$ B$のy座標を求めよ.
(2)点$ C $の座標を求めよ.
(3)直線$ EG $の傾きを求めよ.
$ \boxed{3}$
図のように,底面の半径が3cm,母線の長さが5cmの円錐の中に半径の等しい2つの球$ P,Q $があります.
2つの球$ P,Q $は互いに接し,円錐の底面と側面に接しているとき,次の問いに答えなさい.
ただし,2つの球の中心と,円錐の頂点と,円錐の底面の中心は同じ平面上にあるものとする.
(1)球$ P$の半径を求めよ.
(2)円錐の体積は,$ P $の体積の何倍か.
(3)球$ P $と円錐の側面が接する点を$ A $とする.
点$ A $を通り,円錐の底面に平行な平面で球$ P $を切断するとき,球$ P $の切断面の面積を求めよ.
【作問者の掌(てのひら)で踊る…!】平方根:城北高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt{2023\times2021-4044+2}$の値を求めよ.
城北高校過去問
この動画を見る
$ \sqrt{2023\times2021-4044+2}$の値を求めよ.
城北高校過去問
よく間違える平方根

生徒に解かせると勘違いして間違える問題です。平方根の小数部分 中央大附属

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt {15}$の小数部分と$6-\sqrt{15}$の小数部分との積を求めよ。
中央大学附属高校
この動画を見る
$\sqrt {15}$の小数部分と$6-\sqrt{15}$の小数部分との積を求めよ。
中央大学附属高校
西暦"2023"を含む入試予想問題(その4)~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#数と式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$N$の整数部分が$ N=\sqrt{2023+x}$とする.
整数$x$はいくつあるか.
この動画を見る
$N$の整数部分が$ N=\sqrt{2023+x}$とする.
整数$x$はいくつあるか.
ルートのかけ算

単元:
#数学(中学生)#中3数学#平方根
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{99} \times \sqrt{110} \times \sqrt{30}$
この動画を見る
$\sqrt{99} \times \sqrt{110} \times \sqrt{30}$
西暦"2023"を含む入試予想問題(その2)~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt{2023}x+\sqrt{2021}y=2,\sqrt{2021}x+\sqrt{2023}y=1$
$ x^2-y^2=\Box $である.
この動画を見る
$ \sqrt{2023}x+\sqrt{2021}y=2,\sqrt{2021}x+\sqrt{2023}y=1$
$ x^2-y^2=\Box $である.
【「式の形」が見えればOK!】平方根:東京都立国立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right)^2+ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right) \left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)-\left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)^2$を計算せよ.
都立国立高校過去問
この動画を見る
$ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right)^2+ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right) \left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)-\left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)^2$を計算せよ.
都立国立高校過去問
眠れない夜に学ぶ数学~全国入試問題解法 #shorts #数学 #sound

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x-\dfrac{\sqrt2-2}{2}$のとき,$x^2+2x+\dfrac{1}{x+1}+1$の値を求めなさい.
立命館高校過去問
この動画を見る
$ x-\dfrac{\sqrt2-2}{2}$のとき,$x^2+2x+\dfrac{1}{x+1}+1$の値を求めなさい.
立命館高校過去問
【よく出題される形式!4問分の解説】平方根:群馬県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
数について述べた次のア~エのうち,正しいものをすべて選びなさい.
ア すべての自然数は,その逆数も自然数となる.
イ 異なる2つの整数について,大きい方から小さい方をひいた差は,いつでも自然数となる.
ウ すべての2次方程式の解は,無理数となる.
エ すべての有理数や無理数は,数直線上に対応する点がある.
群馬県高校過去問
この動画を見る
数について述べた次のア~エのうち,正しいものをすべて選びなさい.
ア すべての自然数は,その逆数も自然数となる.
イ 異なる2つの整数について,大きい方から小さい方をひいた差は,いつでも自然数となる.
ウ すべての2次方程式の解は,無理数となる.
エ すべての有理数や無理数は,数直線上に対応する点がある.
群馬県高校過去問
【数学】有理化がなぜ必要なのか?解説してみた!

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
有理化って何のためにしてるか知っていますか??
この動画を見る
有理化って何のためにしてるか知っていますか??
【考え込むより、まず手を付けよう!】平方根:桐蔭学園高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の$\Box$に最も適する数字を答えよ.
${(\sqrt3+\sqrt2)^2-(\sqrt3-\sqrt2)^2}^2=\Box$である.
桐蔭学園高等学校
この動画を見る
次の$\Box$に最も適する数字を答えよ.
${(\sqrt3+\sqrt2)^2-(\sqrt3-\sqrt2)^2}^2=\Box$である.
桐蔭学園高等学校
【困難は分解せよ!】平方根:桐朋高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\dfrac{(\sqrt{14}-\sqrt6)(\sqrt7+\sqrt3)}{2}-(\sqrt2+1)^2$を計算せよ.
桐朋高校過去問
この動画を見る
$\dfrac{(\sqrt{14}-\sqrt6)(\sqrt7+\sqrt3)}{2}-(\sqrt2+1)^2$を計算せよ.
桐朋高校過去問
平方根の計算 関西学院

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{\sqrt {0.52^2 - 0.2^2}}{0.4^2}$
関西学院
この動画を見る
$\frac{\sqrt {0.52^2 - 0.2^2}}{0.4^2}$
関西学院
【中学数学】数学検定3級2次:問題6

単元:
#数学(中学生)#中3数学#平方根#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題6.次の問いに答えなさい。
(13) nを正の整数とします。$\sqrt{120n}$が正の整数となるようなnの最小値を求めなさい。
(14) $x=\sqrt6+\sqrt2,y=\sqrt6-\sqrt2$のとき、$x^2-y^2$の値を求めなさい。
この動画を見る
問題6.次の問いに答えなさい。
(13) nを正の整数とします。$\sqrt{120n}$が正の整数となるようなnの最小値を求めなさい。
(14) $x=\sqrt6+\sqrt2,y=\sqrt6-\sqrt2$のとき、$x^2-y^2$の値を求めなさい。
【「難しい」の原因を探す旅!】平方根:國學院大學久我山高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$a=\dfrac{1}{4}$のとき,
$\dfrac{1-a}{\sqrt{a^2+2a+1}+\sqrt{9a^2-6a+1}}=\Box$
$\Box$を適当にうめなさい.
國學院大學久我山高等学校過去問
この動画を見る
$a=\dfrac{1}{4}$のとき,
$\dfrac{1-a}{\sqrt{a^2+2a+1}+\sqrt{9a^2-6a+1}}=\Box$
$\Box$を適当にうめなさい.
國學院大學久我山高等学校過去問
