2次関数
2次関数
【受験対策】数学－関数１７
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように,関数$y=ax^2$のグラフ上に点$A$がある.
点$A$の$x$座標が2のとき,次の問いに答えなさい.
ただし,$a\gt 0$とする.
①点$A$の$y$座標が6のとき,$a$の値を求めなさい.
②$a=2$とする.
直線$y=2x+b$が点$A$をとおるとき,$b$の値を求めなさい.
③点$A$と$y$軸について,対称な点を$B$とする.
また,$y$軸上に$y$座標が$-1$となる点$C$をとる.
$\triangle ABC$が直角二等辺三角形となるとき,
$a$の値を求めなさい.
図は動画内参照
この動画を見る
右の図のように,関数$y=ax^2$のグラフ上に点$A$がある.
点$A$の$x$座標が2のとき,次の問いに答えなさい.
ただし,$a\gt 0$とする.
①点$A$の$y$座標が6のとき,$a$の値を求めなさい.
②$a=2$とする.
直線$y=2x+b$が点$A$をとおるとき,$b$の値を求めなさい.
③点$A$と$y$軸について,対称な点を$B$とする.
また,$y$軸上に$y$座標が$-1$となる点$C$をとる.
$\triangle ABC$が直角二等辺三角形となるとき,
$a$の値を求めなさい.
図は動画内参照
【受験対策】数学－関数１６
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
図のように,関数$y = ax^2$ グラフ上に,点$A(4,8)$がある.
また,点$B$,点$C$は$y$軸上の点で,
$\triangle ABC$は$AB = AC = 5$ の二等辺三角形である.
このとき,次の各問いに答えなさい.
①$a$の値を求めなさい.
②点$A$から$y$軸に垂線$AD$をひく.
この関数のグラフ上で,点$A$と原点$O$の間に点$P$をとり,
$\triangle ABC$の面積と$\triangle ADP$の面積が等しくなるようにする.
このとき,点$P$の$x$座標を求めなさい.
③点$C$を通り,$AB$に平行な直線と,この関数のグラフの交点のうち,
$x$座標が負である点を$E$とし,$EC$の延長と点$A$から
$x$軸にひいた垂線との交点を$F$とする.
このとき,②における点$P$において,
$\triangle OEF$の面積は$\triangle OPC$の面積の何倍か
求めなさい.
図は動画内参照
この動画を見る
図のように,関数$y = ax^2$ グラフ上に,点$A(4,8)$がある.
また,点$B$,点$C$は$y$軸上の点で,
$\triangle ABC$は$AB = AC = 5$ の二等辺三角形である.
このとき,次の各問いに答えなさい.
①$a$の値を求めなさい.
②点$A$から$y$軸に垂線$AD$をひく.
この関数のグラフ上で,点$A$と原点$O$の間に点$P$をとり,
$\triangle ABC$の面積と$\triangle ADP$の面積が等しくなるようにする.
このとき,点$P$の$x$座標を求めなさい.
③点$C$を通り,$AB$に平行な直線と,この関数のグラフの交点のうち,
$x$座標が負である点を$E$とし,$EC$の延長と点$A$から
$x$軸にひいた垂線との交点を$F$とする.
このとき,②における点$P$において,
$\triangle OEF$の面積は$\triangle OPC$の面積の何倍か
求めなさい.
図は動画内参照
【受験対策】数学－関数１４
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①右の図1で,曲線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフである.
四角形$ABCD$は正方形で,頂点$A$と頂点$D$は曲線上,
頂点$B$と頂点$C$は$x$軸上にある.
このとき,頂点$A$の座標を求めなさい.
②右の図2は,関数$y=ax^2(a\lt 0)$のグラフで,2点$A,B$は,
このグラフ上の点で,$x$座標はそれぞれ$-3,1$である.
2点$A,B$を通る直線の傾きが$3$のとき,$a$の値を求めなさい.
図は動画内参照
この動画を見る
①右の図1で,曲線$\ell$は関数$y=\dfrac{1}{4}x^2$のグラフである.
四角形$ABCD$は正方形で,頂点$A$と頂点$D$は曲線上,
頂点$B$と頂点$C$は$x$軸上にある.
このとき,頂点$A$の座標を求めなさい.
②右の図2は,関数$y=ax^2(a\lt 0)$のグラフで,2点$A,B$は,
このグラフ上の点で,$x$座標はそれぞれ$-3,1$である.
2点$A,B$を通る直線の傾きが$3$のとき,$a$の値を求めなさい.
図は動画内参照
【受験対策】数学－関数１３
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように,関数$y=x^2･･･(ア)$のグラフ上に2点,$A,B$がある.
軸上に点$C$をとり,四角形$ADBC$が平行四辺形となるように,点,$D$をとる.
点$A(-3.9)$,点$B(2.4)$のとき,次の各問いに答えなさい.
ただし,点$C$の$y$座標は,点$A$の$y$座標より大きいものとし,
座標の1目もりを1cmとする.
①関数②について,$x$の値が$-3$から$-1$まで増加するときの
変化の割合を求めなさい.
②関数③について,$x$の変域が$-1\leqq x\leqq 4$のとき,
$y$の変域を求めなさい.
③2点$A,B$を通る直線の式を求めなさい.
④平行四辺形$ADBC$の面積が$24cm^2$となるとき,
点$D$の座標を求めなさい.
図は動画内参照
この動画を見る
右の図のように,関数$y=x^2･･･(ア)$のグラフ上に2点,$A,B$がある.
軸上に点$C$をとり,四角形$ADBC$が平行四辺形となるように,点,$D$をとる.
点$A(-3.9)$,点$B(2.4)$のとき,次の各問いに答えなさい.
ただし,点$C$の$y$座標は,点$A$の$y$座標より大きいものとし,
座標の1目もりを1cmとする.
①関数②について,$x$の値が$-3$から$-1$まで増加するときの
変化の割合を求めなさい.
②関数③について,$x$の変域が$-1\leqq x\leqq 4$のとき,
$y$の変域を求めなさい.
③2点$A,B$を通る直線の式を求めなさい.
④平行四辺形$ADBC$の面積が$24cm^2$となるとき,
点$D$の座標を求めなさい.
図は動画内参照
【中１ P.128】４編の力だめし
中学数学（2次関数）【篠原好】
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
中３向け数学「２次関数」についての説明です。
※図式・数式は動画内参照
この動画を見る
中３向け数学「２次関数」についての説明です。
※図式・数式は動画内参照
【受験対策】 数学－関数⑤
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図のように、関数$y=\displaystyle \frac{1}{2}x^2$のグラフ上に、 3点A、B、Cがあり、
点Bのx座標は2、点Cのx座標は4である。
また、y軸上に点、D(0.8)がある。
四角形ABCDが 平行四辺形となるとき、次の問いに答えよう。
①点Aの座標は?
②直線BDの式は?
③平行四辺形ABCDの面積は?
④原点Oを通り、平行四辺形ABCDの
面積を2等分する直線の式は?
※図は動画内参照
この動画を見る
右の図のように、関数$y=\displaystyle \frac{1}{2}x^2$のグラフ上に、 3点A、B、Cがあり、
点Bのx座標は2、点Cのx座標は4である。
また、y軸上に点、D(0.8)がある。
四角形ABCDが 平行四辺形となるとき、次の問いに答えよう。
①点Aの座標は?
②直線BDの式は?
③平行四辺形ABCDの面積は?
④原点Oを通り、平行四辺形ABCDの
面積を2等分する直線の式は?
※図は動画内参照
【受験対策】 数学－関数③
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図で曲線は$y=x^2$のグラフです。
動点Pは原点Oからと軸上を正の方向に毎秒4の速さで移動し、
動点Qは原点OからX軸上を正の方向に毎秒2の速さで移動します。
①動点P、Qが同時に出発して2秒後にできる直線PQの式は?
②①でもとめた直線PQと曲線との2つの交点において、X座標が負の点をR もう一方をSとするとき、2点R、Sの座標は?
③線分RSの長さは?
※図は動画内参照
この動画を見る
右の図で曲線は$y=x^2$のグラフです。
動点Pは原点Oからと軸上を正の方向に毎秒4の速さで移動し、
動点Qは原点OからX軸上を正の方向に毎秒2の速さで移動します。
①動点P、Qが同時に出発して2秒後にできる直線PQの式は?
②①でもとめた直線PQと曲線との2つの交点において、X座標が負の点をR もう一方をSとするとき、2点R、Sの座標は?
③線分RSの長さは?
※図は動画内参照
【受験対策】 数学－規則性②
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
同じ長さのマッチ棒を用いて、下の図のように、一定の規則にしたがって、1番目、2番目3番目、…とマッチ棒をつなぎ合わせて図形をつくっていく。
用いたマッチ棒の数は、1番目では16本、2番目では36本 3番目では64本である。
①4番目の図形をつくるには何本のマッチ棒が必要?
②n番目の図形をつくるには何本のマッチ棒が必要か、nの式で表そう。
※図は動画内参照
この動画を見る
同じ長さのマッチ棒を用いて、下の図のように、一定の規則にしたがって、1番目、2番目3番目、…とマッチ棒をつなぎ合わせて図形をつくっていく。
用いたマッチ棒の数は、1番目では16本、2番目では36本 3番目では64本である。
①4番目の図形をつくるには何本のマッチ棒が必要?
②n番目の図形をつくるには何本のマッチ棒が必要か、nの式で表そう。
※図は動画内参照
【受験対策】 数学－規則性①
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
同じ長さのマッチ棒を用いて、下の図のように、一定の規則にしたがって、1番目、2番目、3番目、…とマッチ棒をつなぎ合わせて図形をつくっていく。
用いたマッチ棒の数は1番目では4本、2番目では12本、 3番目では24本である。
①5番目の図形をつくるには何本のマッチ棒が必要?
②14番目の図形をつくるには何本のマッチ棒が必要?
③n番目の図形をつくるには何本のマッチ棒が必要か、nの式で表そう。
※図は動画内参照
この動画を見る
同じ長さのマッチ棒を用いて、下の図のように、一定の規則にしたがって、1番目、2番目、3番目、…とマッチ棒をつなぎ合わせて図形をつくっていく。
用いたマッチ棒の数は1番目では4本、2番目では12本、 3番目では24本である。
①5番目の図形をつくるには何本のマッチ棒が必要?
②14番目の図形をつくるには何本のマッチ棒が必要?
③n番目の図形をつくるには何本のマッチ棒が必要か、nの式で表そう。
※図は動画内参照
【受験対策】 数学－関数②
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
右の図で、曲線は関数$y=x^2$のグラフです。
曲線上の 点A(-2.4)を通り、傾きが-1、1の直線と曲線との交点、をそれぞれB、Cとします。
点P、Qは点Aを同時に出発して、点Pは線分AB上を、点Qは線分AC上を、それぞれ一定の速さで進み、 点Pは点Bに、点Qは点Cに同時に到着しました。
①点Pがy軸上にきたときの点Qの座標は?
②点P、Qが同時に到着した後、点P、Qは線分BC上をそれぞれの速さを変えずに進み、線分BC上の点Rで出会いました。
点Rの座標は?
③△ABRの面積を求めよう。
ただし、座標軸の単位の長さを1cmとします。
※図は動画内参照
この動画を見る
右の図で、曲線は関数$y=x^2$のグラフです。
曲線上の 点A(-2.4)を通り、傾きが-1、1の直線と曲線との交点、をそれぞれB、Cとします。
点P、Qは点Aを同時に出発して、点Pは線分AB上を、点Qは線分AC上を、それぞれ一定の速さで進み、 点Pは点Bに、点Qは点Cに同時に到着しました。
①点Pがy軸上にきたときの点Qの座標は?
②点P、Qが同時に到着した後、点P、Qは線分BC上をそれぞれの速さを変えずに進み、線分BC上の点Rで出会いました。
点Rの座標は?
③△ABRの面積を求めよう。
ただし、座標軸の単位の長さを1cmとします。
※図は動画内参照
【数学】中3-42 二次関数の利用④(一次関数との交点編)
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎右の図のように、$y=x^2$と$y=x+6$が2点A,Bで交わっている。
①点Aと点Bの座標は？
②△AODの面積は？
③△AOBの面積は？
※図は動画内参照
この動画を見る
◎右の図のように、$y=x^2$と$y=x+6$が2点A,Bで交わっている。
①点Aと点Bの座標は？
②△AODの面積は？
③△AOBの面積は？
※図は動画内参照
【数学】中3-41 二次関数の利用③(一次関数とのコラボ編)
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎右の図のように、$y=ax^2$のグラフに、2点A,Bがある。
点Aは(-4,8)で、点Bのx座標は2である。
①aの値は？
②点Bの座標は？
③2点A,Bを通る直線の式は？
④△AOBの面積は？
⑤直線A,B場を動く点Pがある。
直線OPが△AOBの面積を2等分するとき、点Pの座標は？
※図は動画内参照
この動画を見る
◎右の図のように、$y=ax^2$のグラフに、2点A,Bがある。
点Aは(-4,8)で、点Bのx座標は2である。
①aの値は？
②点Bの座標は？
③2点A,Bを通る直線の式は？
④△AOBの面積は？
⑤直線A,B場を動く点Pがある。
直線OPが△AOBの面積を2等分するとき、点Pの座標は？
※図は動画内参照
【数学】中3-40 二次関数の利用②(動点編)
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎右の図のような、AB=4cm、AD=8cmの長方形がある。
点PはAB上を、秒速1cmの速さでAからBまで動き、 点QはAD上を秒速2cmの速さで AからDまで動く。
2点P,Qが同時に,Aを出発してからx秒後の△APQの面積をy$cm^2$とする。
① xとyの関係を式で表すと？
② xの変域は？
③ yの変域は？
④ ①の式をグラフに書くと？
(通る座標を確認してね！)
※図は動画内参照
この動画を見る
◎右の図のような、AB=4cm、AD=8cmの長方形がある。
点PはAB上を、秒速1cmの速さでAからBまで動き、 点QはAD上を秒速2cmの速さで AからDまで動く。
2点P,Qが同時に,Aを出発してからx秒後の△APQの面積をy$cm^2$とする。
① xとyの関係を式で表すと？
② xの変域は？
③ yの変域は？
④ ①の式をグラフに書くと？
(通る座標を確認してね！)
※図は動画内参照
【数学】中3-39 二次関数の利用①(平均の速さ編)
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
◎物を落下させるとき、落下しはじめてからx秒間に落下する距離
をymとすると、yはxの2乗に比例する。
落下しはじめてから2秒間で20m落下したとき、次の①～④を解こう!
①xとyの関係を式に表すと?
②落下しはじめてから6秒間 では何m落下する?
③90mのところから落下すると、地上に落ちるまでに何秒かかる?
④落下しはじめてから、2秒後から5秒後までの 平均の速さは?
この動画を見る
◎物を落下させるとき、落下しはじめてからx秒間に落下する距離
をymとすると、yはxの2乗に比例する。
落下しはじめてから2秒間で20m落下したとき、次の①～④を解こう!
①xとyの関係を式に表すと?
②落下しはじめてから6秒間 では何m落下する?
③90mのところから落下すると、地上に落ちるまでに何秒かかる?
④落下しはじめてから、2秒後から5秒後までの 平均の速さは?
【数学】中3-38 二次関数の変化の割合
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$y=ax^2$について、xの値がbからcまで増加したときの変化の割合は①＿＿＿＿で求めよう！
②$y=3x^2$について、xの値が-2から5 まで増加するときの変化の割合は?
③$-\displaystyle \frac{1}{2}x^2$について、xの値が3から7 まで増加するときの変化の割合は?
④$-\displaystyle \frac{1}{3}x^2$について、Xの値がtから $t +1$まで増加するときの変化の割合が -5のとき、tの値はいくつ?
⑤$y=ax^2$について、xの値が-5から3 まで増加するときの変化の割合が、 $y=-3x+6$の変化の割合と等しくなった。
aの値はいくつ?
この動画を見る
$y=ax^2$について、xの値がbからcまで増加したときの変化の割合は①＿＿＿＿で求めよう！
②$y=3x^2$について、xの値が-2から5 まで増加するときの変化の割合は?
③$-\displaystyle \frac{1}{2}x^2$について、xの値が3から7 まで増加するときの変化の割合は?
④$-\displaystyle \frac{1}{3}x^2$について、Xの値がtから $t +1$まで増加するときの変化の割合が -5のとき、tの値はいくつ?
⑤$y=ax^2$について、xの値が-5から3 まで増加するときの変化の割合が、 $y=-3x+6$の変化の割合と等しくなった。
aの値はいくつ?
【数学】中3-37 二次関数の変域
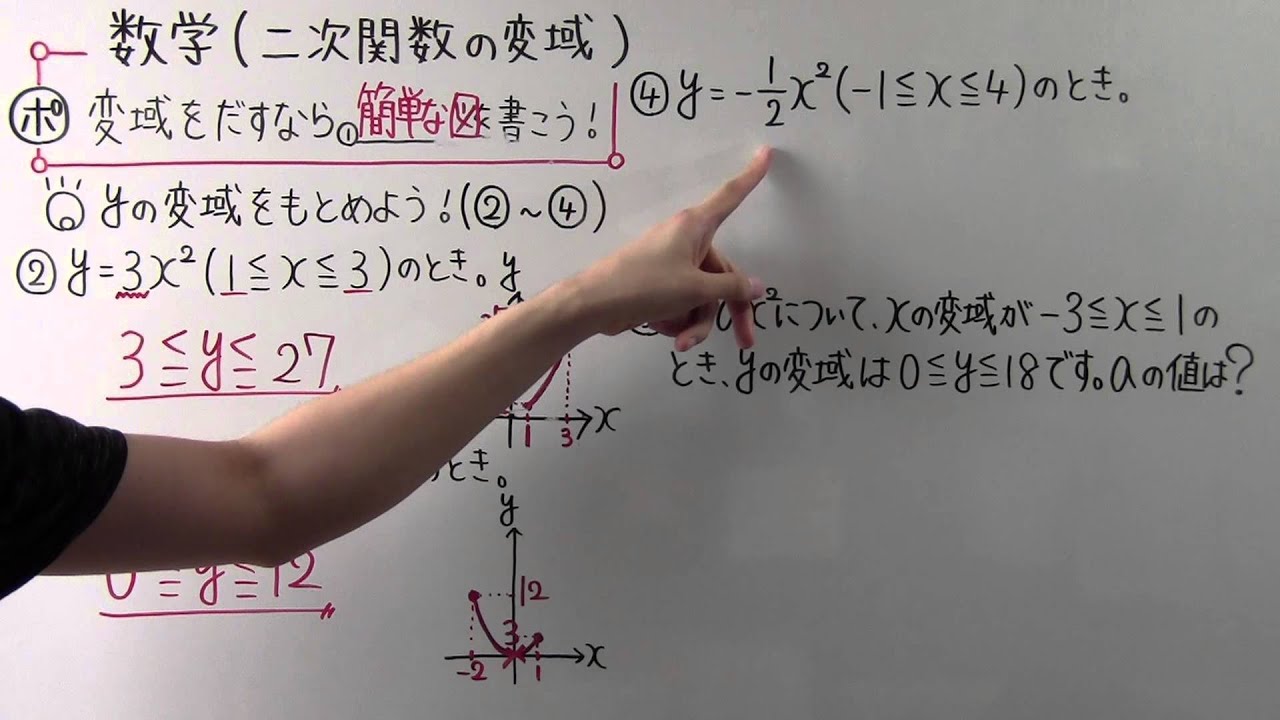
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
変域をだすなら①＿＿＿＿を書こう！
◎yの変域をもとめよう!(②～④) )のとき。
②$y=3x^2(1 \leqq x \leqq 3)$のとき。
③$y=3x^2(-2\leqq x \leqq 1)$のとき。
④$y=-\displaystyle \frac{1}{2}x^2(-1\leqq x \leqq4)$のとき。
⑤$y=ax^2$について、xの変域が$-3 \leqq x \leqq 1$のとき、
yの変域は$0 \leqq y \leqq 18$です。
aの値は？
この動画を見る
変域をだすなら①＿＿＿＿を書こう！
◎yの変域をもとめよう!(②～④) )のとき。
②$y=3x^2(1 \leqq x \leqq 3)$のとき。
③$y=3x^2(-2\leqq x \leqq 1)$のとき。
④$y=-\displaystyle \frac{1}{2}x^2(-1\leqq x \leqq4)$のとき。
⑤$y=ax^2$について、xの変域が$-3 \leqq x \leqq 1$のとき、
yの変域は$0 \leqq y \leqq 18$です。
aの値は？
【数学】中3-36 二次関数のグラフ②
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
$\boxed{A}～\boxed{D}$の関数からあてはまるものをすべて書こう！
$\boxed{A} y=3x^2$
$\boxed{B} y=-\displaystyle \frac{1}{5}x^2$
$\boxed{C} y=-x^2$
$\boxed{D} y=\displaystyle \frac{2}{3}x^2$
①グラフが下に開いているのは？
②グラフの開き方が一番大きいのは？
③グラフが$y=x^2$とx軸を対象の軸として線対称になっているのはどれ？
④$x=0$のとき、yが最小になるのは？
⑤$x＜0$の範囲で、xの値が増加するとyの値が減少するのは？
⑥$\boxed{ア}～\boxed{エ}$の中で、$\boxed{C}$と$\boxed{D}$のグラフはどれ？
$\boxed{C}$→ 、$\boxed{D}$→
※グラフは動画内参照
この動画を見る
$\boxed{A}～\boxed{D}$の関数からあてはまるものをすべて書こう！
$\boxed{A} y=3x^2$
$\boxed{B} y=-\displaystyle \frac{1}{5}x^2$
$\boxed{C} y=-x^2$
$\boxed{D} y=\displaystyle \frac{2}{3}x^2$
①グラフが下に開いているのは？
②グラフの開き方が一番大きいのは？
③グラフが$y=x^2$とx軸を対象の軸として線対称になっているのはどれ？
④$x=0$のとき、yが最小になるのは？
⑤$x＜0$の範囲で、xの値が増加するとyの値が減少するのは？
⑥$\boxed{ア}～\boxed{エ}$の中で、$\boxed{C}$と$\boxed{D}$のグラフはどれ？
$\boxed{C}$→ 、$\boxed{D}$→
※グラフは動画内参照
【数学】中3-35 二次関数のグラフ①
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
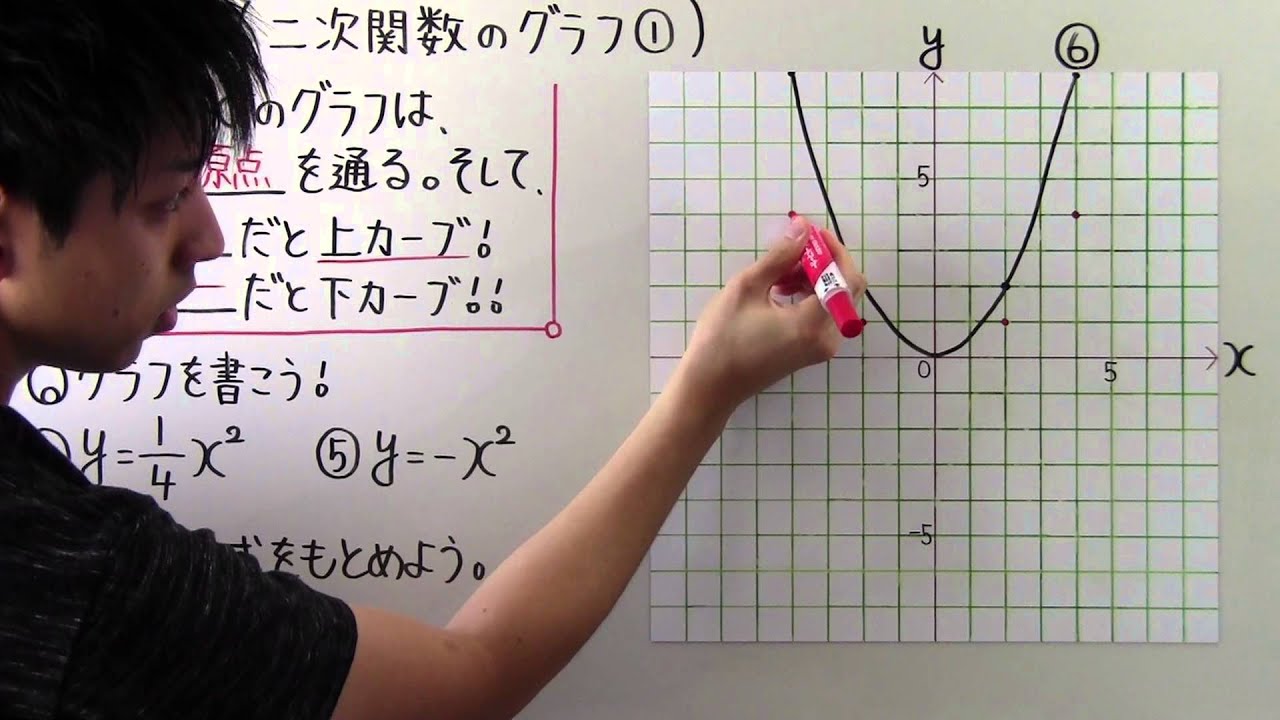
$y=ax^2$のグラフは、 必ず①＿＿＿＿を通る。
そしてaが＿＿＿＿だと上カーブ!
aが③＿＿＿＿だと下カーブ!!
◎グラフを書こう!
④$y=\displaystyle \frac{1}{4}x^2$
⑤$y=-x^2$
⑥グラフの式をもとめよう。
※グラフは動画内参照
この動画を見る
$y=ax^2$のグラフは、 必ず①＿＿＿＿を通る。
そしてaが＿＿＿＿だと上カーブ!
aが③＿＿＿＿だと下カーブ!!
◎グラフを書こう!
④$y=\displaystyle \frac{1}{4}x^2$
⑤$y=-x^2$
⑥グラフの式をもとめよう。
※グラフは動画内参照
【数学】中3-33 二次関数って？
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
y=①＿＿＿＿で表されるとき、
『yはXの②＿＿＿＿に③＿＿＿＿する』といって、
このときのaを④＿＿＿＿という。
◎xとyの関係を式に表そう!
⑤ １辺がxcmの正方形の面積y$cm^2$。
⑥ １辺がxcmの立方体の体積y$cm^3$。
⑦ １辺がxcmの立方体の表面積y$cm^2$。
⑧底辺xcm、高さ8cmの 三角形の面積y$cm^2$。
⑨半径xcmの円 の面積y$cm^2$。
⑩底面が1辺2xcmの正方形、高さが6cm の正四角錐の体積y$cm^2$。
⑪ ⑤～⑩のうち、yがxの2乗に比例するのは?
この動画を見る
y=①＿＿＿＿で表されるとき、
『yはXの②＿＿＿＿に③＿＿＿＿する』といって、
このときのaを④＿＿＿＿という。
◎xとyの関係を式に表そう!
⑤ １辺がxcmの正方形の面積y$cm^2$。
⑥ １辺がxcmの立方体の体積y$cm^3$。
⑦ １辺がxcmの立方体の表面積y$cm^2$。
⑧底辺xcm、高さ8cmの 三角形の面積y$cm^2$。
⑨半径xcmの円 の面積y$cm^2$。
⑩底面が1辺2xcmの正方形、高さが6cm の正四角錐の体積y$cm^2$。
⑪ ⑤～⑩のうち、yがxの2乗に比例するのは?
【数学】中3-34 二次関数の式をもとめよう
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
二次関数といえば、y=①＿＿＿＿
◎xとyの関係を式に表そう。
②yはxの2乗に比例し、x=-2のときy=24。
③yはxの2乗に比例し、x=-4のとき、y=-8。
◎次の値をだそう。
④yはxの2乗に比例し、x=-3のときy=-4である。
x=2のとき、yの値は？
⑤yはxの2乗に比例し、x=2のときy=-3である。
y=12のときxの値は？
この動画を見る
二次関数といえば、y=①＿＿＿＿
◎xとyの関係を式に表そう。
②yはxの2乗に比例し、x=-2のときy=24。
③yはxの2乗に比例し、x=-4のとき、y=-8。
◎次の値をだそう。
④yはxの2乗に比例し、x=-3のときy=-4である。
x=2のとき、yの値は？
⑤yはxの2乗に比例し、x=2のときy=-3である。
y=12のときxの値は？
【For you 動画－５】 中３－二次関数
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
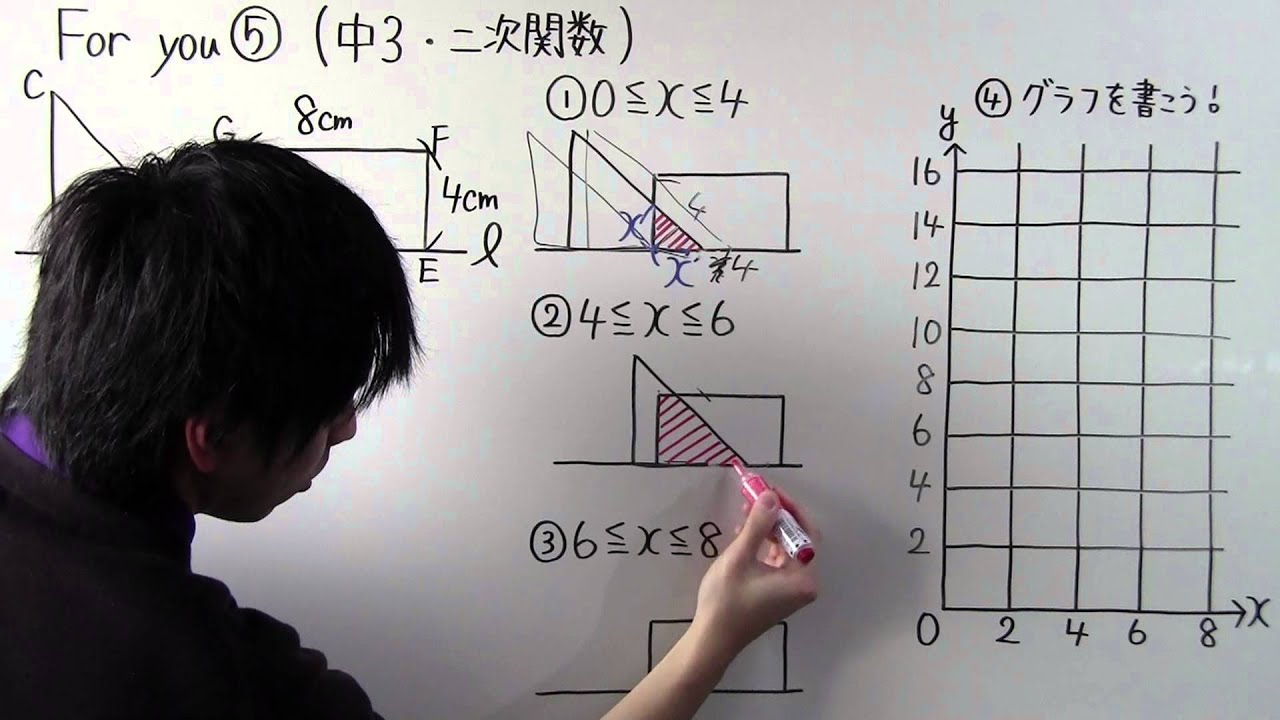
4点、$A、B、D、E$は直線上にある。
$AB=BC=6cm$の直角二等辺三角形$ABC$が毎秒$1cm$の速さで上を右に動く。
点$A$が点$D$に重なった瞬間を○秒とする。 このとき、$x$秒後の$2$つの図形が重なる部分の面積を$ycm²$とする。
次の場合について、$y$を$x$の式で表そう!
①$0 \leqq x \leqq 4$
②$4 \leqq x \leqq 6$
③$6 \leqq x \leqq 8$
④グラフを書こう!
※図は動画内参照
この動画を見る
4点、$A、B、D、E$は直線上にある。
$AB=BC=6cm$の直角二等辺三角形$ABC$が毎秒$1cm$の速さで上を右に動く。
点$A$が点$D$に重なった瞬間を○秒とする。 このとき、$x$秒後の$2$つの図形が重なる部分の面積を$ycm²$とする。
次の場合について、$y$を$x$の式で表そう!
①$0 \leqq x \leqq 4$
②$4 \leqq x \leqq 6$
③$6 \leqq x \leqq 8$
④グラフを書こう!
※図は動画内参照
【For you 動画－４（追加）】 中３数学－別解答バージョン
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
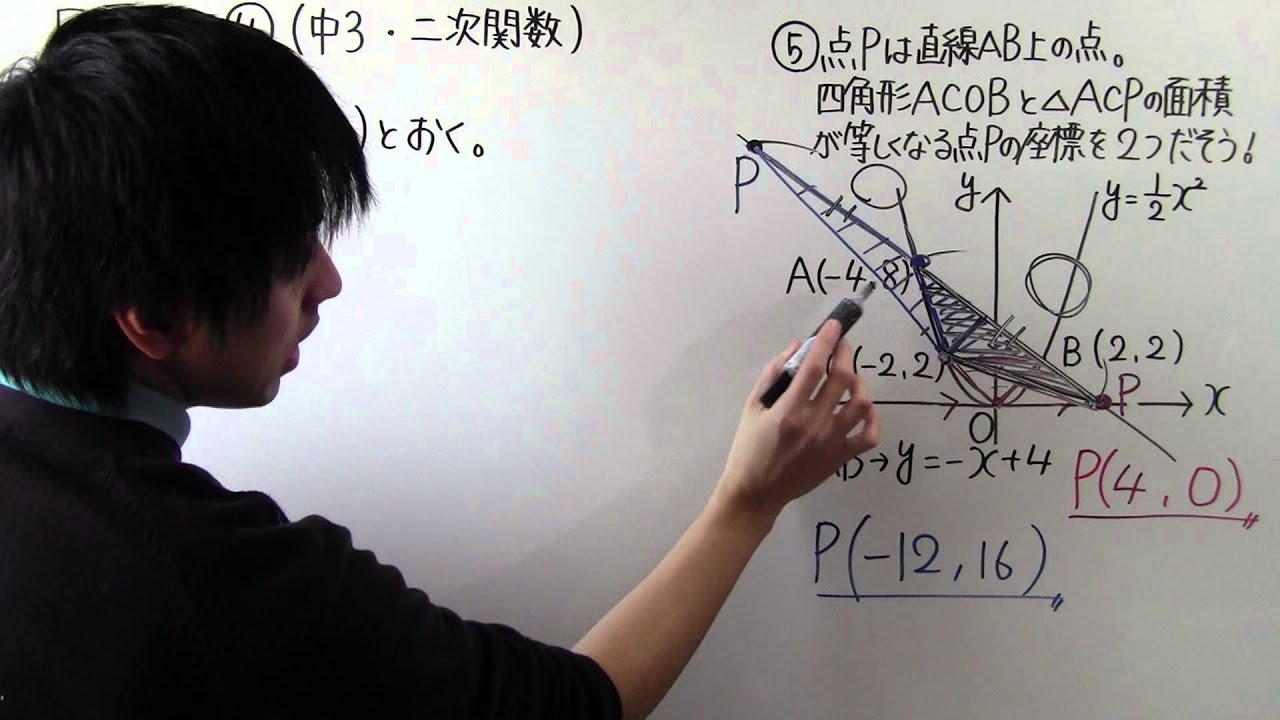
【別解】
$P(x、y)$とおく。
$P(x、y)$、$(4,0)$の中点が$(-4,8)$
$\displaystyle \frac{x+4}{2}=-4 → x+4=-8$
$x=-12$
$\displaystyle \frac{y+\xcancel{0}}{2}=8 → y=16$
※図は動画内参照
この動画を見る
【別解】
$P(x、y)$とおく。
$P(x、y)$、$(4,0)$の中点が$(-4,8)$
$\displaystyle \frac{x+4}{2}=-4 → x+4=-8$
$x=-12$
$\displaystyle \frac{y+\xcancel{0}}{2}=8 → y=16$
※図は動画内参照
【For you動画－４】 中３数学－二次関数
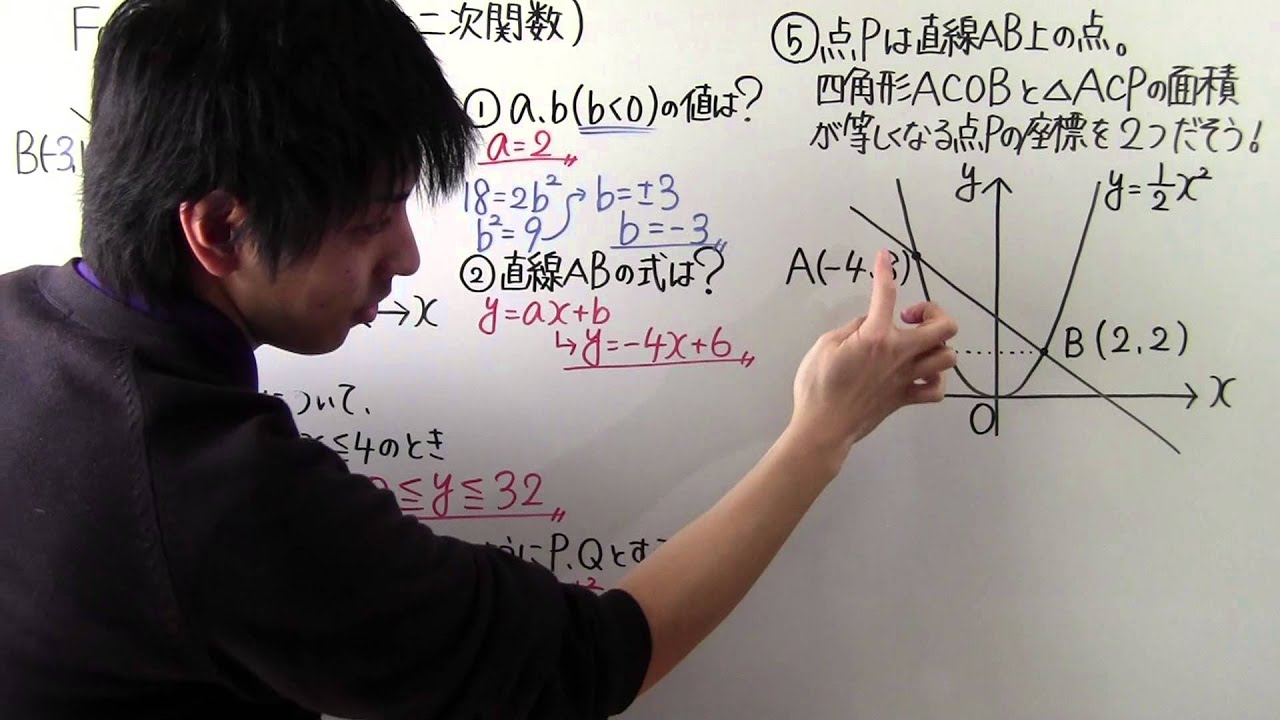
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
問いに答えよ。
①$a.b(b \lt 0)$の値は?
②直線$AB$の式は?
③図の二次関数について、 $X$の変域が$-2 \leqq x \leqq 4$のときその変域は?
④$X=t$の直線をひき、交点を図のように$P.Q$とする。
$PQ=8$となるしをだそう!
ただし-3 \leqq t \leqq 1とする。
⑤点$P$は直線$AB$上の点。
四角形$ACOB$と$\triangle ACP$の面積
が等しくなる点$P$の座標を$2$つだそう!
※図は動画内参照
この動画を見る
問いに答えよ。
①$a.b(b \lt 0)$の値は?
②直線$AB$の式は?
③図の二次関数について、 $X$の変域が$-2 \leqq x \leqq 4$のときその変域は?
④$X=t$の直線をひき、交点を図のように$P.Q$とする。
$PQ=8$となるしをだそう!
ただし-3 \leqq t \leqq 1とする。
⑤点$P$は直線$AB$上の点。
四角形$ACOB$と$\triangle ACP$の面積
が等しくなる点$P$の座標を$2$つだそう!
※図は動画内参照
【中２ 数学】 ２－③⑨ 一次関数の利用③ ・ 動点編
単元：
#数学(中学生)#中３数学#2次関数
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
中２ 数学 一次関数の利用③ ・ 動点編
以下の問に答えよ
毎秒1cmで A → B → C → D (動点 P ) 、△ ADP が y ㎠
① 動点 P が AB 上
② 動点 P が BC 上
③ 動点 P が CD 上
※図は動画内参照
この動画を見る
中２ 数学 一次関数の利用③ ・ 動点編
以下の問に答えよ
毎秒1cmで A → B → C → D (動点 P ) 、△ ADP が y ㎠
① 動点 P が AB 上
② 動点 P が BC 上
③ 動点 P が CD 上
※図は動画内参照