 中3数学
中3数学
 中3数学
中3数学
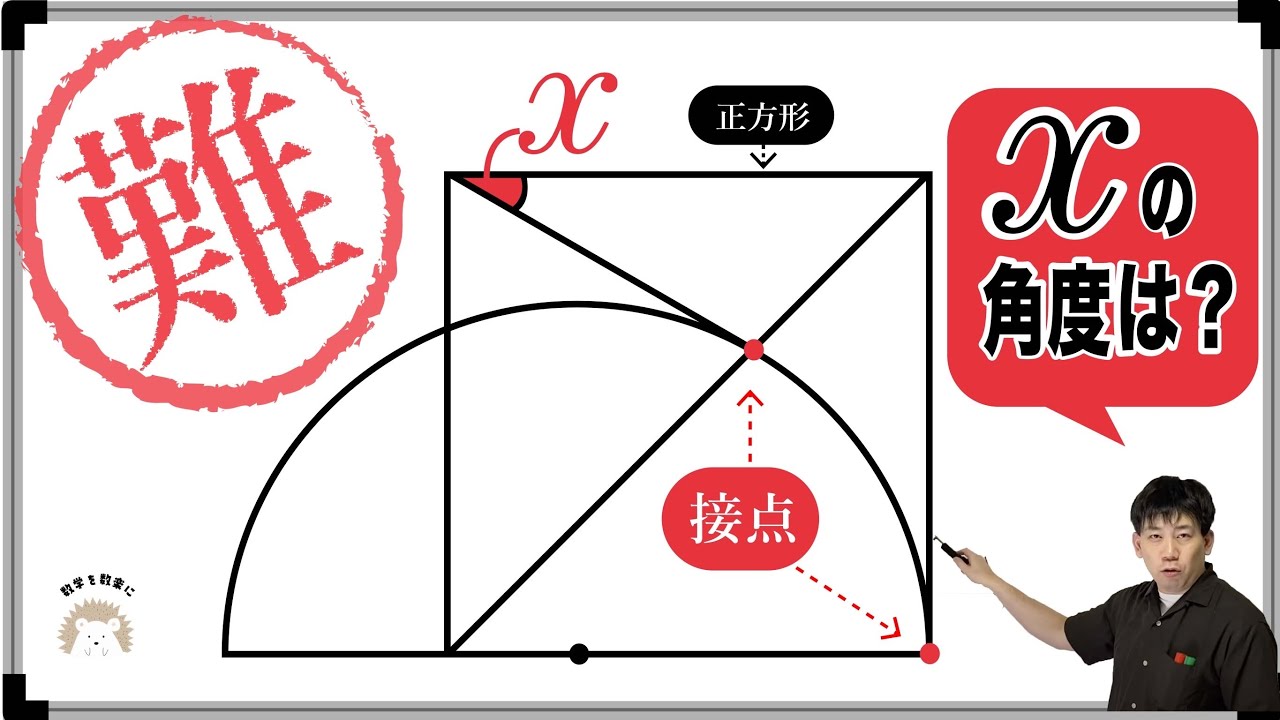
半円と正方形 難です。
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x =?$
*図は動画内参照
灘高等学校
この動画を見る
$\angle x =?$
*図は動画内参照
灘高等学校
【高校受験対策/数学】死守83

単元:
#数学(中学生)#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#比例・反比例#空間図形#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守83
①$-1-5$を計算しなさい。
②$(-3)^2+4×(-2)$を計算しなさい。
③$10xy^2÷ (-5y)×3x$を計算しなさい。
④$2x-y-\frac{5x+y}{3}$を計算しなさい。
⑤$(\sqrt{5}+3)(\sqrt{5}-2)$を計算しなさい。
⑥次の方程式を解きなさい。
$x^2=9x$
⑦$l=2\pi r$を$r$について解きなさい。
⑧正$n$角形の1つの内角が$140°$であるとき、$n$の値を求めなさい。
⑨$y$は$x$に比例し、$x=-3$のとき、$y=18$である。
$x=\frac{1}{2}$のときの$y$の値を求めなさい。
➉空間内の平面について述べた文として適切でないものを、次のア~エの中から1つ選びその記号を書きなさい。
ア 一直線上にある3点をふくむ平面は1つに決まる。
イ 交わる2直線をふくむ平面は1つに決まる。
ウ 平行な2直線をふくむ平面は1つに決まる。
エ 1つの直線とその直線上にない1点をふくむ平面は1つに決まる。
この動画を見る
高校受験対策・死守83
①$-1-5$を計算しなさい。
②$(-3)^2+4×(-2)$を計算しなさい。
③$10xy^2÷ (-5y)×3x$を計算しなさい。
④$2x-y-\frac{5x+y}{3}$を計算しなさい。
⑤$(\sqrt{5}+3)(\sqrt{5}-2)$を計算しなさい。
⑥次の方程式を解きなさい。
$x^2=9x$
⑦$l=2\pi r$を$r$について解きなさい。
⑧正$n$角形の1つの内角が$140°$であるとき、$n$の値を求めなさい。
⑨$y$は$x$に比例し、$x=-3$のとき、$y=18$である。
$x=\frac{1}{2}$のときの$y$の値を求めなさい。
➉空間内の平面について述べた文として適切でないものを、次のア~エの中から1つ選びその記号を書きなさい。
ア 一直線上にある3点をふくむ平面は1つに決まる。
イ 交わる2直線をふくむ平面は1つに決まる。
ウ 平行な2直線をふくむ平面は1つに決まる。
エ 1つの直線とその直線上にない1点をふくむ平面は1つに決まる。
初見で解けたら認めよう。2通りで解説。
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#方べきの定理と2つの円の関係#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
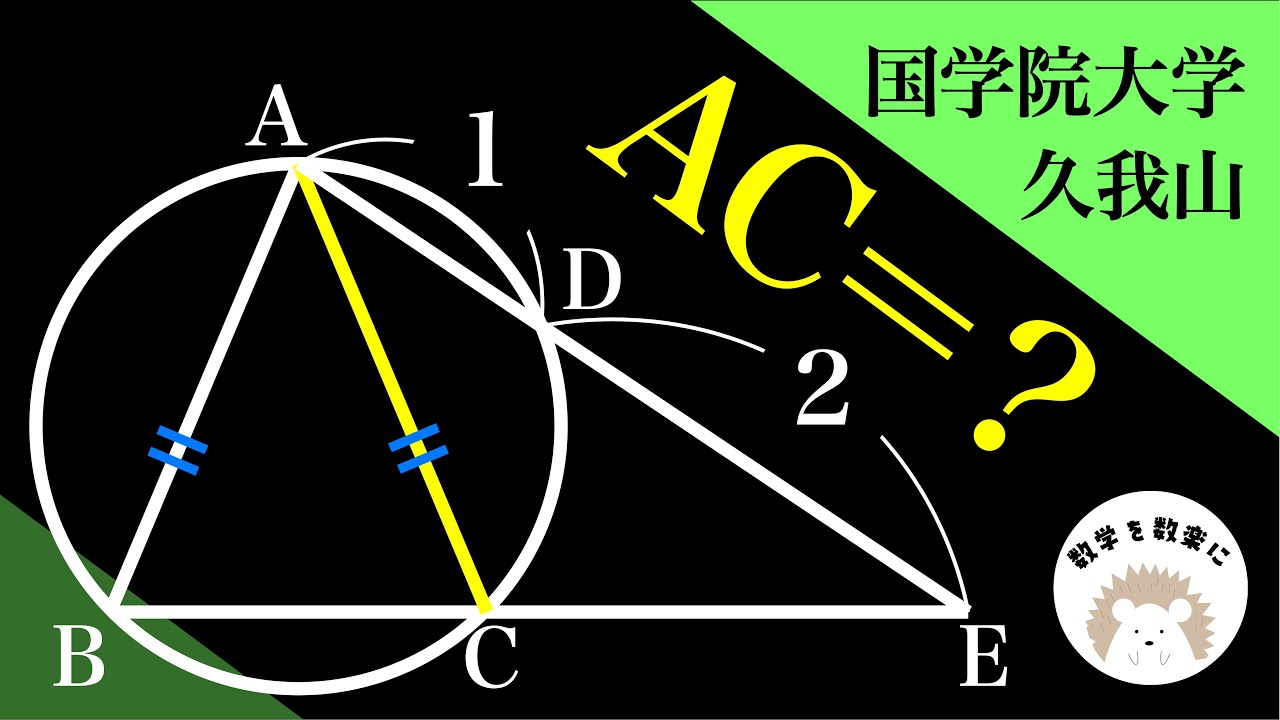
AC=?
*図は動画内参照
國學院大學久我山高等学校
この動画を見る
AC=?
*図は動画内参照
國學院大學久我山高等学校
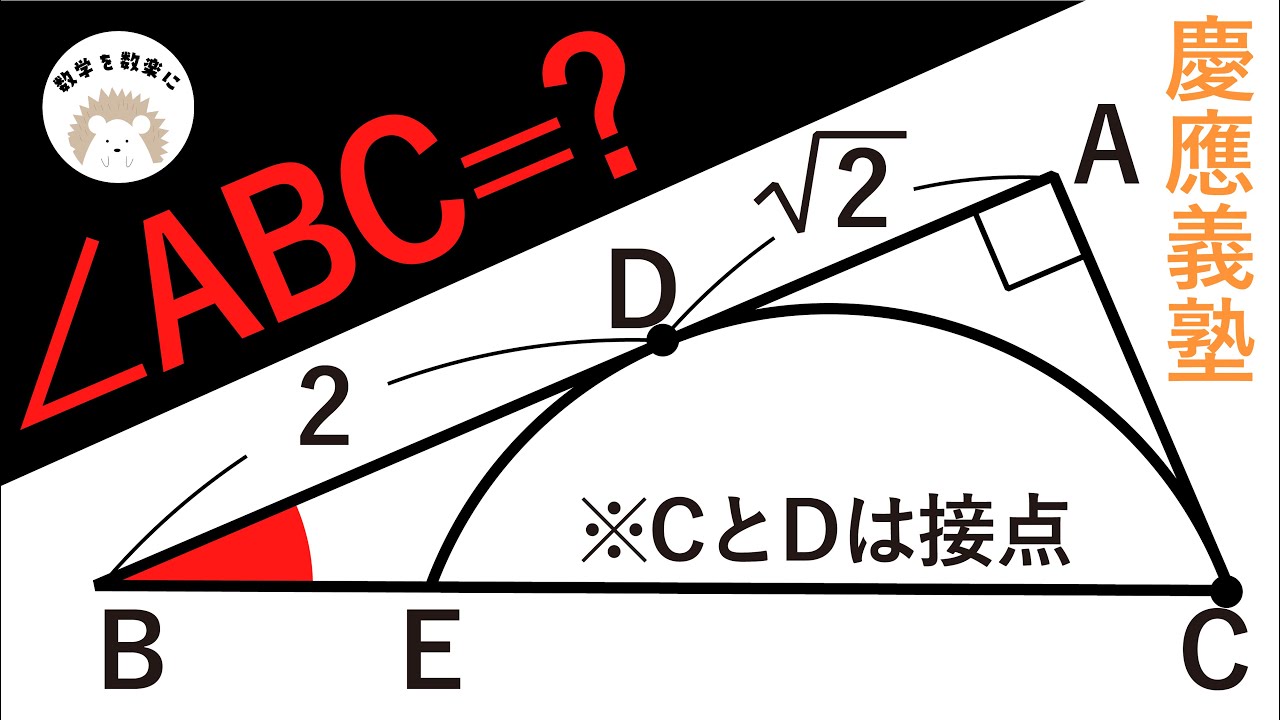
円と接線と角度 慶應義塾高校
単元:
#数学(中学生)#中3数学#数A#図形の性質#円#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Cと点Dは接点
$\angle ABC=?$
*図は動画内参照
慶應義塾高等学校
この動画を見る
点Cと点Dは接点
$\angle ABC=?$
*図は動画内参照
慶應義塾高等学校
ルートの大小関係
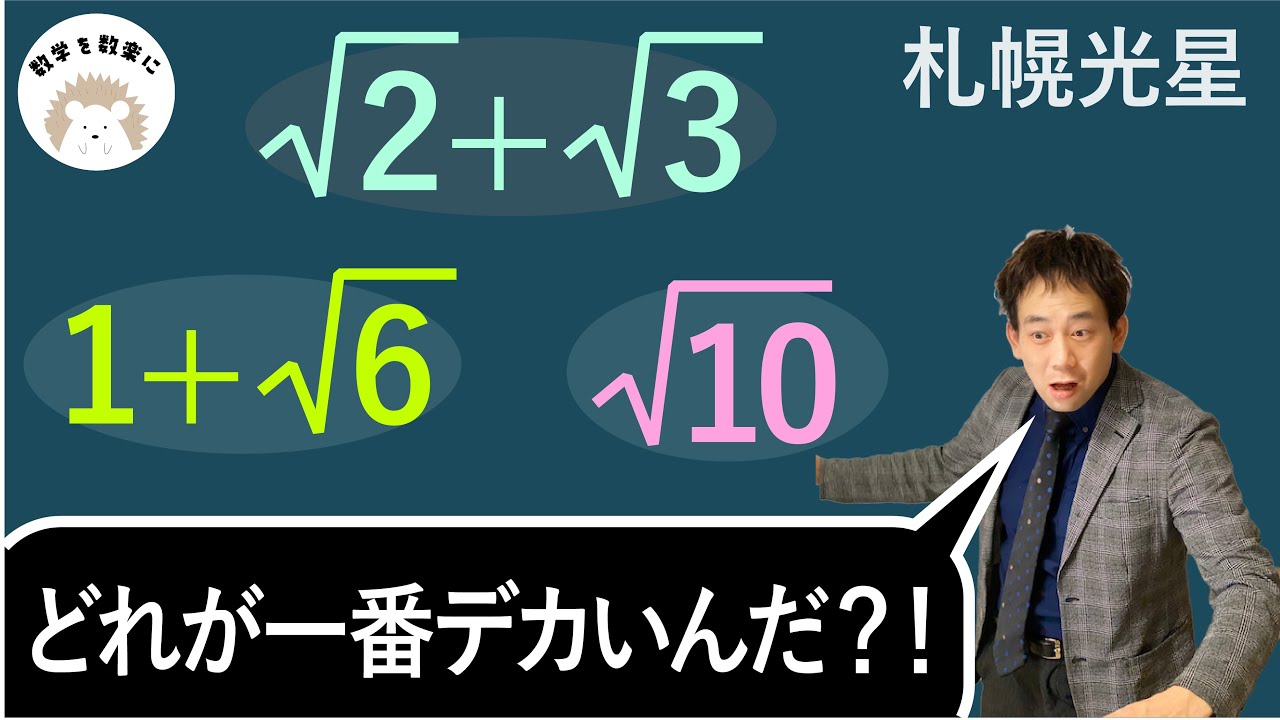
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt 2 + \sqrt 3$ , $1 + \sqrt 6$ , $\sqrt {10}$
どれが一番大きい?
札幌光星高等学校
この動画を見る
$\sqrt 2 + \sqrt 3$ , $1 + \sqrt 6$ , $\sqrt {10}$
どれが一番大きい?
札幌光星高等学校
【高校受験対策/数学】死守82

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#資料の活用#1次関数#文字と式#平面図形#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守82
①$3-(-6)$を計算しなさい。
②$9÷(-\frac{1}{5})+4$を計算しなさい。
③$\sqrt{28}-\sqrt{7}$を計算しなさい。
④下の図のように、半径が$9cm$、中心角が$60°$のおうぎ形$OAB$があります。
このおうぎ形の弧$AB$の長さを求めなさい。
ただし円周率は$\pi$を用いなさい。
⑤右の表は、A中学校の3年生男子80人の立ち幅とびの記録を度数分布表にまと めたものです。
度数が最も多い階級の相対度数を求めなさい。
⑥関数$y=3x$のグラフに平行で、 点$(0,2)$を通る直線の式を求めなさい。
⑦右の図の四角形$ABCD$において、点$B$と点$Dが$重なるように折ったときにできる折り目の線と
辺$AB$、$BC$との交点をそれぞれ$P,Q$とします。
2点$P,Q$を定規とコンパスを使って作図しなさい。
ただし、点を示す記号$P,Q$をかき入れ、作図に用いた線は消さないこと。
この動画を見る
高校受験対策・死守82
①$3-(-6)$を計算しなさい。
②$9÷(-\frac{1}{5})+4$を計算しなさい。
③$\sqrt{28}-\sqrt{7}$を計算しなさい。
④下の図のように、半径が$9cm$、中心角が$60°$のおうぎ形$OAB$があります。
このおうぎ形の弧$AB$の長さを求めなさい。
ただし円周率は$\pi$を用いなさい。
⑤右の表は、A中学校の3年生男子80人の立ち幅とびの記録を度数分布表にまと めたものです。
度数が最も多い階級の相対度数を求めなさい。
⑥関数$y=3x$のグラフに平行で、 点$(0,2)$を通る直線の式を求めなさい。
⑦右の図の四角形$ABCD$において、点$B$と点$Dが$重なるように折ったときにできる折り目の線と
辺$AB$、$BC$との交点をそれぞれ$P,Q$とします。
2点$P,Q$を定規とコンパスを使って作図しなさい。
ただし、点を示す記号$P,Q$をかき入れ、作図に用いた線は消さないこと。
【中学数学】2次方程式の演習~2021年度成城学園高等学校~【高校受験】

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\displaystyle \frac{(x + 7) ^ 2 - (x - 7) ^ 2}{12} = \displaystyle \frac{1}{4}x^ 2 +\displaystyle \frac{1}{3}x+4$
この動画を見る
$\displaystyle \frac{(x + 7) ^ 2 - (x - 7) ^ 2}{12} = \displaystyle \frac{1}{4}x^ 2 +\displaystyle \frac{1}{3}x+4$
【裏技】これ知ってたん?

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$y=\displaystyle \frac{1}{2}x^2$について
$x$が2から4まで増加するときの変化の割合を求めよ。
この動画を見る
$y=\displaystyle \frac{1}{2}x^2$について
$x$が2から4まで増加するときの変化の割合を求めよ。
超気持ちいい!!気付けば一瞬!!帝京大学高校

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-2x-1 = 0$のとき
$x^2(x-1)^2(x-2)^2$ =
帝京大学高等学校
この動画を見る
$x^2-2x-1 = 0$のとき
$x^2(x-1)^2(x-2)^2$ =
帝京大学高等学校
高校入試の因数分解最高峰

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-32x-y^2-8y+240$を因数分解せよ
立命館高等学校
この動画を見る
$x^2-32x-y^2-8y+240$を因数分解せよ
立命館高等学校
【中学数学】2次関数の変化の割合の裏技~圧倒的時短~ 4-4【中3数学】

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
関数$y=\displaystyle \frac{1}{2}x^2$について、$x$が2から4増加するときの変化の割合を求めよ。
2⃣
関数$y=2x^2$の$x$の値が-2から3まで増加するときの変化の割合を求めよ。
3⃣
関数$y=ax^2$で、$x$の値が1から3まで増加するとき、変化の割合が12になった。
このとき、$a$の値を求めよ。
この動画を見る
1⃣
関数$y=\displaystyle \frac{1}{2}x^2$について、$x$が2から4増加するときの変化の割合を求めよ。
2⃣
関数$y=2x^2$の$x$の値が-2から3まで増加するときの変化の割合を求めよ。
3⃣
関数$y=ax^2$で、$x$の値が1から3まで増加するとき、変化の割合が12になった。
このとき、$a$の値を求めよ。
2次方程式と式の値 本郷高校
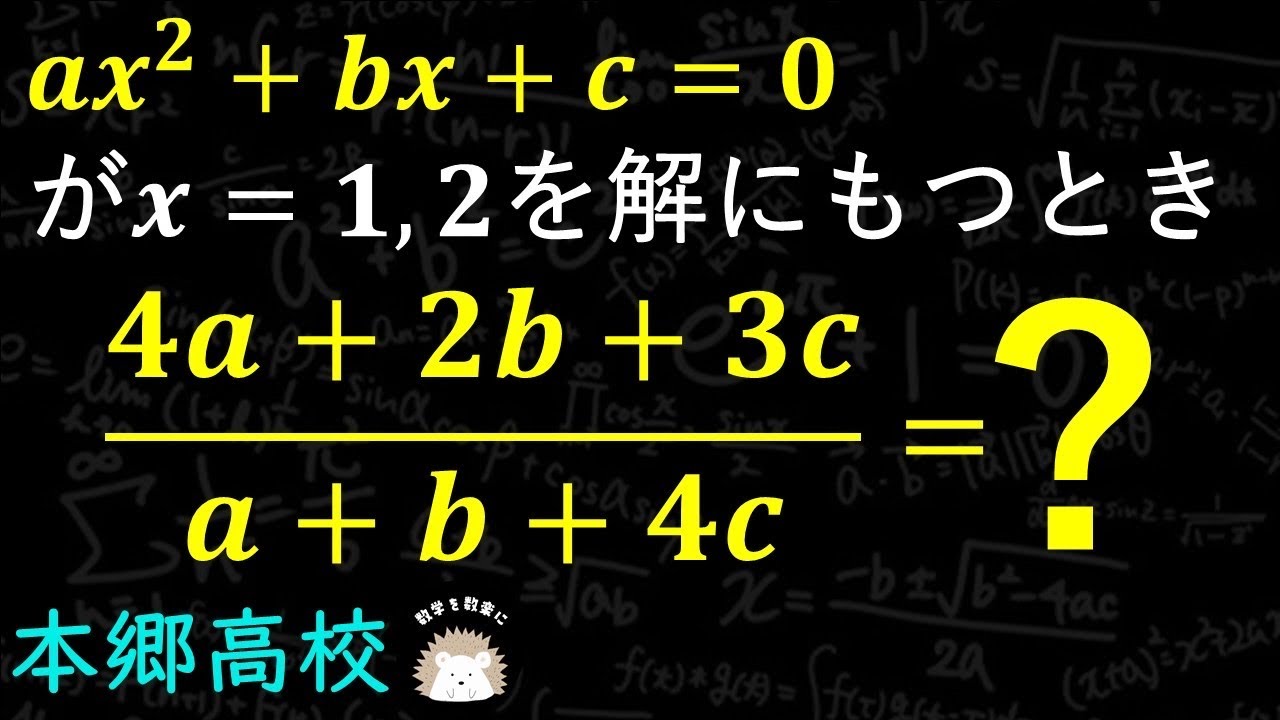
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$ax^2+bx+c=0$がx=1,2を解にもつ
$\frac{4a+2b+3c}{a+b+4c}$
本郷高等学校
この動画を見る
$ax^2+bx+c=0$がx=1,2を解にもつ
$\frac{4a+2b+3c}{a+b+4c}$
本郷高等学校
【高校受験対策/数学】死守81(問題作りました)

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#1次関数#平行と合同#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守81
①$81÷(-3)-(-11)$を計算しなさい。
②次の式を因数分解しなさい。
$(x-2)^2-18(x-2)+81$
③次の連立方程式を解きなさい。
$3x+11y=13$
$2x-3y=19$
④$311x-8y=1$を$y$について解きなさい。
⑤絶対値が$81$である数をすべて書きなさい。
⑥右の図において2直線$l,m$は平行である。
このとき、$\angle x$の大きさを求めなさい。
⑦3点$(-3,-11)$、$(2,9)$、$(k,81)$が一直線上にあるとき、 $k$の値を求めなさい。
⑧定価$8100$円のパーカーが$a$割引で売っていた。
それを買おうとレジに持っていくと、キャンペーンだったようで、そこからさらに$500$円引きしてくれた。
このとき、パーカーを買ったときの代金を$a$を使った式で表しなさい。
ただし消費税については考えないものとする。
この動画を見る
高校受験対策・死守81
①$81÷(-3)-(-11)$を計算しなさい。
②次の式を因数分解しなさい。
$(x-2)^2-18(x-2)+81$
③次の連立方程式を解きなさい。
$3x+11y=13$
$2x-3y=19$
④$311x-8y=1$を$y$について解きなさい。
⑤絶対値が$81$である数をすべて書きなさい。
⑥右の図において2直線$l,m$は平行である。
このとき、$\angle x$の大きさを求めなさい。
⑦3点$(-3,-11)$、$(2,9)$、$(k,81)$が一直線上にあるとき、 $k$の値を求めなさい。
⑧定価$8100$円のパーカーが$a$割引で売っていた。
それを買おうとレジに持っていくと、キャンペーンだったようで、そこからさらに$500$円引きしてくれた。
このとき、パーカーを買ったときの代金を$a$を使った式で表しなさい。
ただし消費税については考えないものとする。
かけて315 桜美林高校
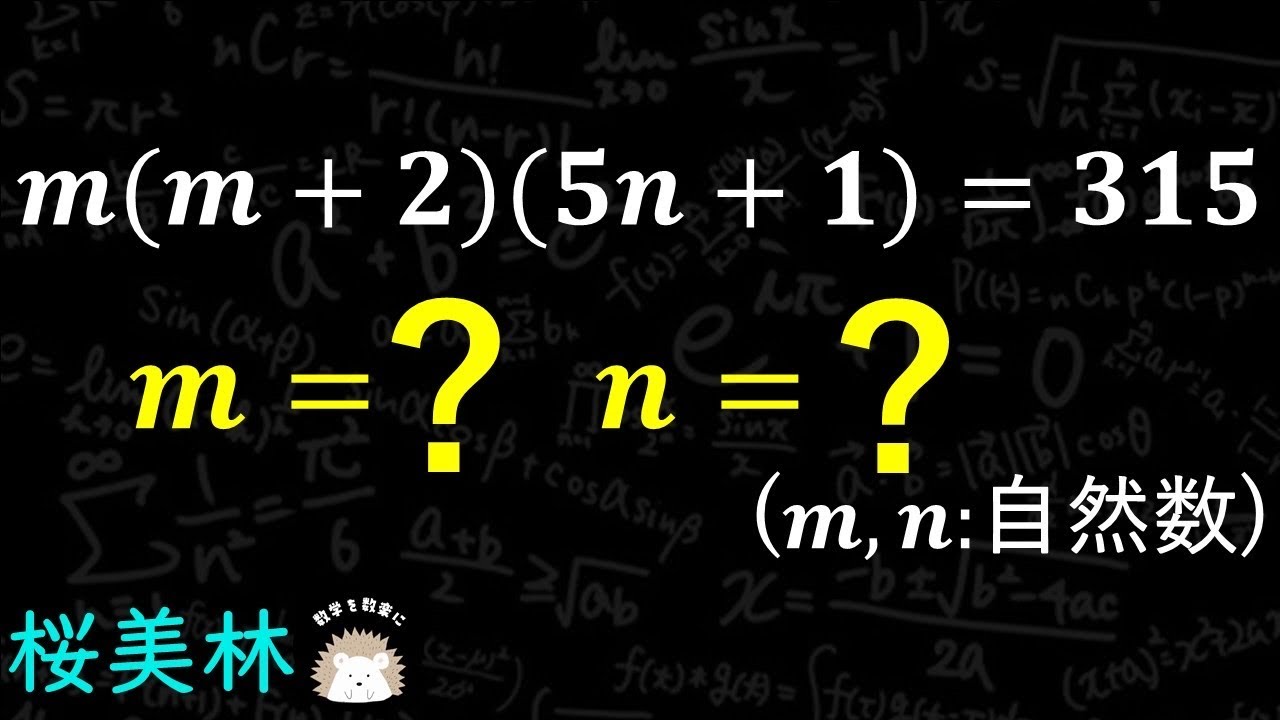
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
m(m+2)(5n+1) =315 (m,nは自然数)
桜美林高等学校
この動画を見る
m(m+2)(5n+1) =315 (m,nは自然数)
桜美林高等学校
【中学数学】2次関数の演習~変化の割合の問題~ 4-3.5【中3数学】

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
関数$y=ax^2$は$x$の値が1から3まで増加するときの変化の割合が6である。
この関数について、$x$の値が3から5まで増加するときの変化の割合を求めよ。
この動画を見る
関数$y=ax^2$は$x$の値が1から3まで増加するときの変化の割合が6である。
この関数について、$x$の値が3から5まで増加するときの変化の割合を求めよ。
【高校受験対策/数学】死守-80

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#2次方程式#空間図形#1次関数#確率#2次関数#文字と式#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守80
①$-3+(-4)×5$を計算しなさい。
②$4xy÷8x×6y$を計算しなさい。
③$\frac{4x-y}{2}-(2x-3y)$を計算しなさい。
④連立方程式を解きなさい。
$5x-4y=9$
$2x-3y=5$
③下の図で、$\angle x$の大きさを求めなさい。
④地球の直径は約$12700km$です。
有効数字が$1,2,7$であるとして、この距離を整数部分が1けたの数と、10の何乗かの積の形で表すと右のようになります。
アとイにあてはまる数を書きなさい。
⑦半径が$2cm$の球の体積と表面積を求めなさい。ただし円周率は$\pi$とする。
⑧赤玉3個と白玉2個が入っている袋があります。
この袋から玉を1個取り出して色を確認して、それを袋に戻してから、もう一度玉を1個取り出して色を確認します。
このとき、2回とも同じ色の玉が出る確率を求めなさい。
ただし、袋の中は見えないものとし、どの玉が出ることも同様に確からしいものとする。
⑨関数$y=ax^2$について、$x$の変域が$-2 \leqq x \leqq 3$のとき、$y$の変域は$-3b \leqq y \leqq 0$となりました。
このとき$a$の値を求めなさい。
この動画を見る
高校受験対策・死守80
①$-3+(-4)×5$を計算しなさい。
②$4xy÷8x×6y$を計算しなさい。
③$\frac{4x-y}{2}-(2x-3y)$を計算しなさい。
④連立方程式を解きなさい。
$5x-4y=9$
$2x-3y=5$
③下の図で、$\angle x$の大きさを求めなさい。
④地球の直径は約$12700km$です。
有効数字が$1,2,7$であるとして、この距離を整数部分が1けたの数と、10の何乗かの積の形で表すと右のようになります。
アとイにあてはまる数を書きなさい。
⑦半径が$2cm$の球の体積と表面積を求めなさい。ただし円周率は$\pi$とする。
⑧赤玉3個と白玉2個が入っている袋があります。
この袋から玉を1個取り出して色を確認して、それを袋に戻してから、もう一度玉を1個取り出して色を確認します。
このとき、2回とも同じ色の玉が出る確率を求めなさい。
ただし、袋の中は見えないものとし、どの玉が出ることも同様に確からしいものとする。
⑨関数$y=ax^2$について、$x$の変域が$-2 \leqq x \leqq 3$のとき、$y$の変域は$-3b \leqq y \leqq 0$となりました。
このとき$a$の値を求めなさい。
素数に関する問題

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$z=x^2-6xy-40y^2$ (x,y,zは素数)のときzの最小値=?
市川高等学校
この動画を見る
$z=x^2-6xy-40y^2$ (x,y,zは素数)のときzの最小値=?
市川高等学校
解ける? 明大明治
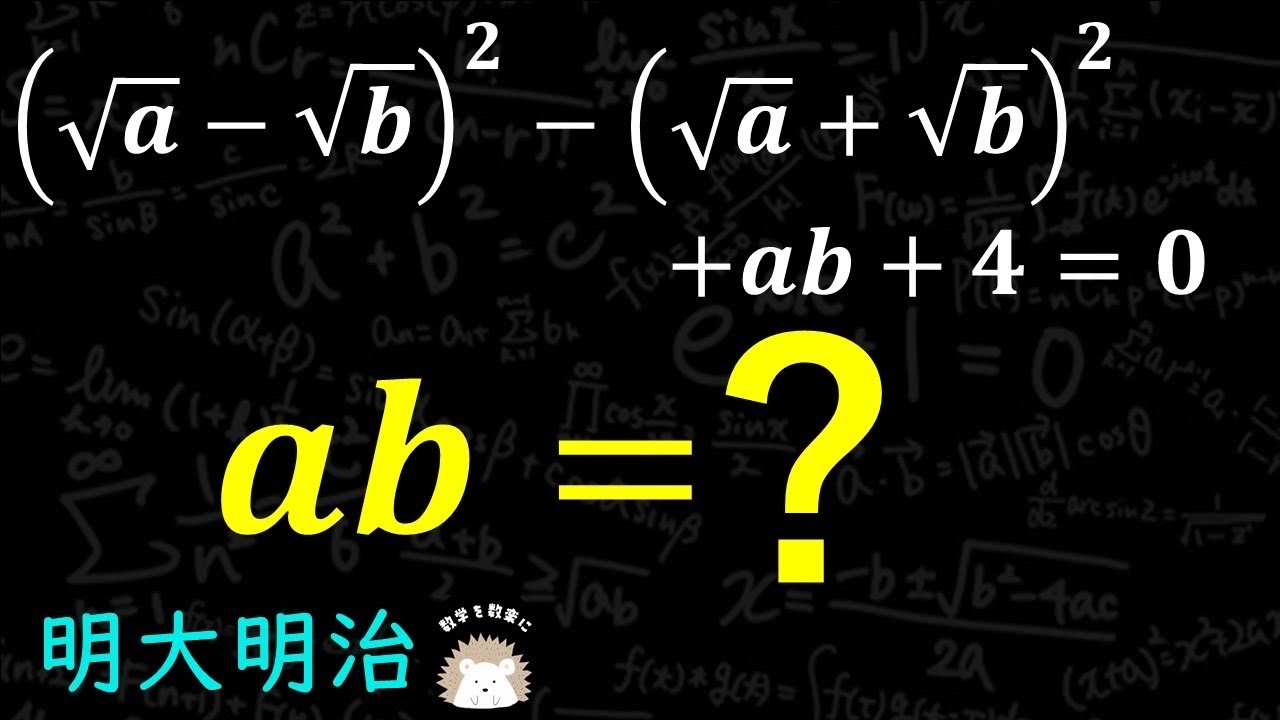
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt a - \sqrt b)^2 - (\sqrt a + \sqrt b)^2 +ab +4 = 0$のとき
ab=?
明治大学付属明治高等学校
この動画を見る
$(\sqrt a - \sqrt b)^2 - (\sqrt a + \sqrt b)^2 +ab +4 = 0$のとき
ab=?
明治大学付属明治高等学校
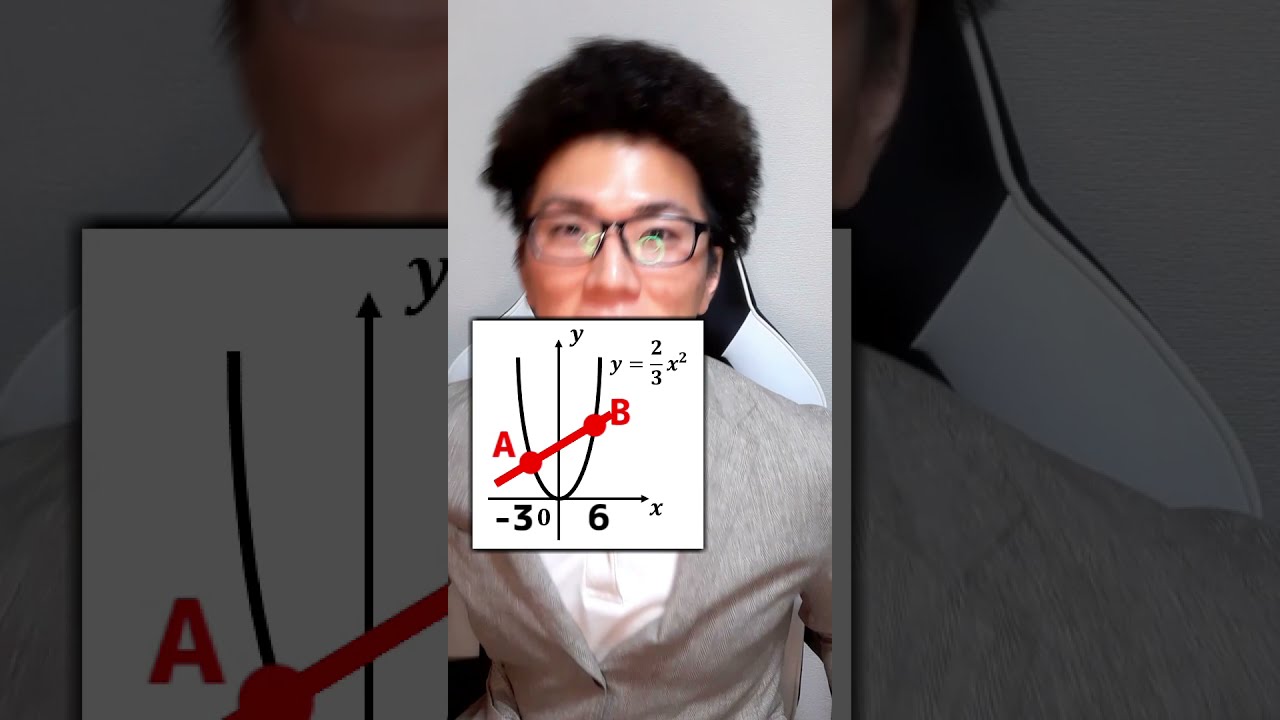
【中学数学】2次関数上の2点を通る直線の裏技の証明【中3数学】

これすごすぎん?
【高校受験対策/数学】死守-79

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#文字と式#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守79
①$-3-(-7)$を計算しなさい。
②$8a^3b^5÷4a^2b^3$を計算しなさい。
③$x^2-8x+16$を因数分解しなさい。
④$a=\frac{2b-c}{5}$を$c$について解きなさい。
⑤二次方程式$x^2+5x+2=0$を解きなさい。
⑥$a=2$、$b=-3$のとき、$a+b^2$の値を求めなさい。
⑦次の文の( )に当てはまる条件として最も適切なものを、ア~エから1つ選んで記号で答えなさい。
平行四辺形$ABCD$に、( )の条件が加わると、平行四辺形$ABCD$は長方形になる。
ア $AB=BC$
イ $AC\perp BD$
ウ $AC=BD$
エ $\angle ABD=\angle CBD$
⑧$A$地点から$B$地点まで、初めは毎分$60m$で$am$歩き、途中から毎分$100m$で$bm$走ったところ、$20$分以内で$B$地点に到着した。この数量の関係を不等式で表しなさい。
⑨次のア~エのうちから、内容が正しいものを1つ選んで記号で答えなさい。
ア $9$の平方根は$3$と$-3$である。
イ $\sqrt{16}$を根号を使わずに表すと$\pm 4$である。
ウ $\sqrt{5}+\sqrt{7}$と$\sqrt{5+7}$は同じ値である。
エ $(\sqrt{2}+\sqrt{6})^2$と$(\sqrt{2})^2+(\sqrt{6})^2$は同じ値である。
この動画を見る
高校受験対策・死守79
①$-3-(-7)$を計算しなさい。
②$8a^3b^5÷4a^2b^3$を計算しなさい。
③$x^2-8x+16$を因数分解しなさい。
④$a=\frac{2b-c}{5}$を$c$について解きなさい。
⑤二次方程式$x^2+5x+2=0$を解きなさい。
⑥$a=2$、$b=-3$のとき、$a+b^2$の値を求めなさい。
⑦次の文の( )に当てはまる条件として最も適切なものを、ア~エから1つ選んで記号で答えなさい。
平行四辺形$ABCD$に、( )の条件が加わると、平行四辺形$ABCD$は長方形になる。
ア $AB=BC$
イ $AC\perp BD$
ウ $AC=BD$
エ $\angle ABD=\angle CBD$
⑧$A$地点から$B$地点まで、初めは毎分$60m$で$am$歩き、途中から毎分$100m$で$bm$走ったところ、$20$分以内で$B$地点に到着した。この数量の関係を不等式で表しなさい。
⑨次のア~エのうちから、内容が正しいものを1つ選んで記号で答えなさい。
ア $9$の平方根は$3$と$-3$である。
イ $\sqrt{16}$を根号を使わずに表すと$\pm 4$である。
ウ $\sqrt{5}+\sqrt{7}$と$\sqrt{5+7}$は同じ値である。
エ $(\sqrt{2}+\sqrt{6})^2$と$(\sqrt{2})^2+(\sqrt{6})^2$は同じ値である。
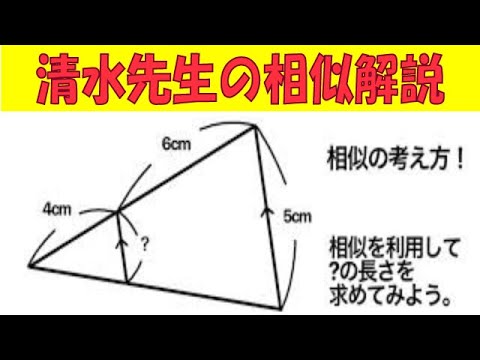
【数学】相似な図形:相似の考え方!
【裏技】これはせこすぎる

【正四面体】正四面体の体積の公式を5分で解説!〔高校数学 数学〕

【中学数学】2次関数上の2点を通る直線の裏技【中3数学】

【高校受験対策/数学】死守-78

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#比例・反比例#1次関数#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守78
①下の図のように、長方形$ABCD$の中に 1辺の長さが$\sqrt{5}cm$と$\sqrt{10}cm$の正方形がある。
このとき、斜線部分の長方形の間の長さを求めなさい。
②葉一くんは、下の図の平行四辺形$ABCD$の面積を求めるために、辺$BC$を底辺とみて、高さを測ろうと考えた。
点を$P$下の図のようにとるとき、線分$PH$が高さとなるような点$H$を作図によって求めなさい。
③1000円で、1個$a$円のクリームパン5個と1個$b$円のジャムパン3個を買うことができる。
ただし消費税は考えないものとする。
この数量の関係を表した不等式としてもっとも適切なものを、次の ア~エの中から一つ選んで、その記号を書きなさい。
ア $1000-(5a+3b) \lt 0$
イ $5a+3b \lt 1000$
ウ $1000-(5a+3b) \geqq 0$
エ $(5a+3b) \geqq 1000$
④ 右の図で、点$A$は関数$y=\frac{2}{x }$と関数$y=ax^2$のグラフの交点である。
点$B$は点$A$を$y$軸を対称の軸として対称移動させたものであり、$x$座標は$-1$である。
このことから、$a$の値はアであり、関数$y=ax^2$について、 $x$の値が1から3まで増加するときの変化の割合はイであることがわ かる。
このとき上のア・イに当てはまる数をそれぞれ書きなさい。
この動画を見る
高校受験対策・死守78
①下の図のように、長方形$ABCD$の中に 1辺の長さが$\sqrt{5}cm$と$\sqrt{10}cm$の正方形がある。
このとき、斜線部分の長方形の間の長さを求めなさい。
②葉一くんは、下の図の平行四辺形$ABCD$の面積を求めるために、辺$BC$を底辺とみて、高さを測ろうと考えた。
点を$P$下の図のようにとるとき、線分$PH$が高さとなるような点$H$を作図によって求めなさい。
③1000円で、1個$a$円のクリームパン5個と1個$b$円のジャムパン3個を買うことができる。
ただし消費税は考えないものとする。
この数量の関係を表した不等式としてもっとも適切なものを、次の ア~エの中から一つ選んで、その記号を書きなさい。
ア $1000-(5a+3b) \lt 0$
イ $5a+3b \lt 1000$
ウ $1000-(5a+3b) \geqq 0$
エ $(5a+3b) \geqq 1000$
④ 右の図で、点$A$は関数$y=\frac{2}{x }$と関数$y=ax^2$のグラフの交点である。
点$B$は点$A$を$y$軸を対称の軸として対称移動させたものであり、$x$座標は$-1$である。
このことから、$a$の値はアであり、関数$y=ax^2$について、 $x$の値が1から3まで増加するときの変化の割合はイであることがわ かる。
このとき上のア・イに当てはまる数をそれぞれ書きなさい。
気持ちがいい式の値 芝浦工大柏
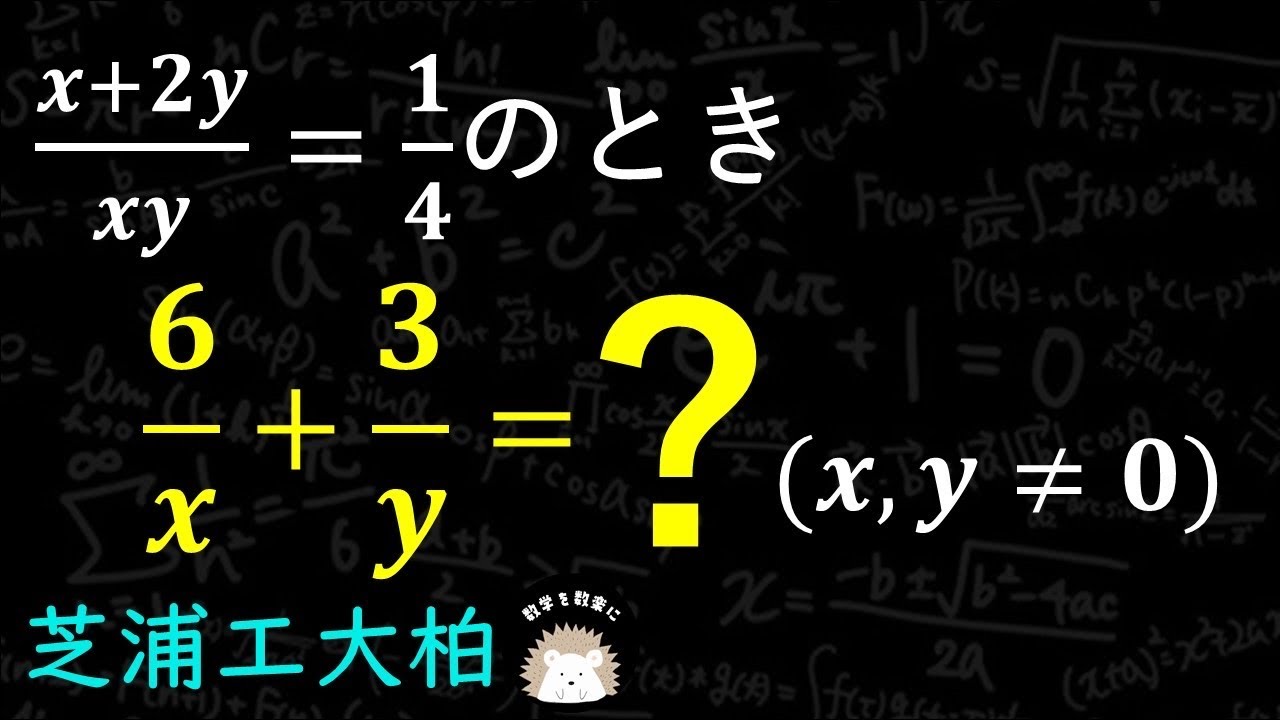
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{x+2y}{xy} = \frac{1}{4}$のとき$\frac{6}{x}+\frac{3}{y} =?$
芝浦工業大学柏高等学校
この動画を見る
$\frac{x+2y}{xy} = \frac{1}{4}$のとき$\frac{6}{x}+\frac{3}{y} =?$
芝浦工業大学柏高等学校
すぐになんの2乗か分かる?

知っていれば一瞬!って訳でもない 日大習志野(改)
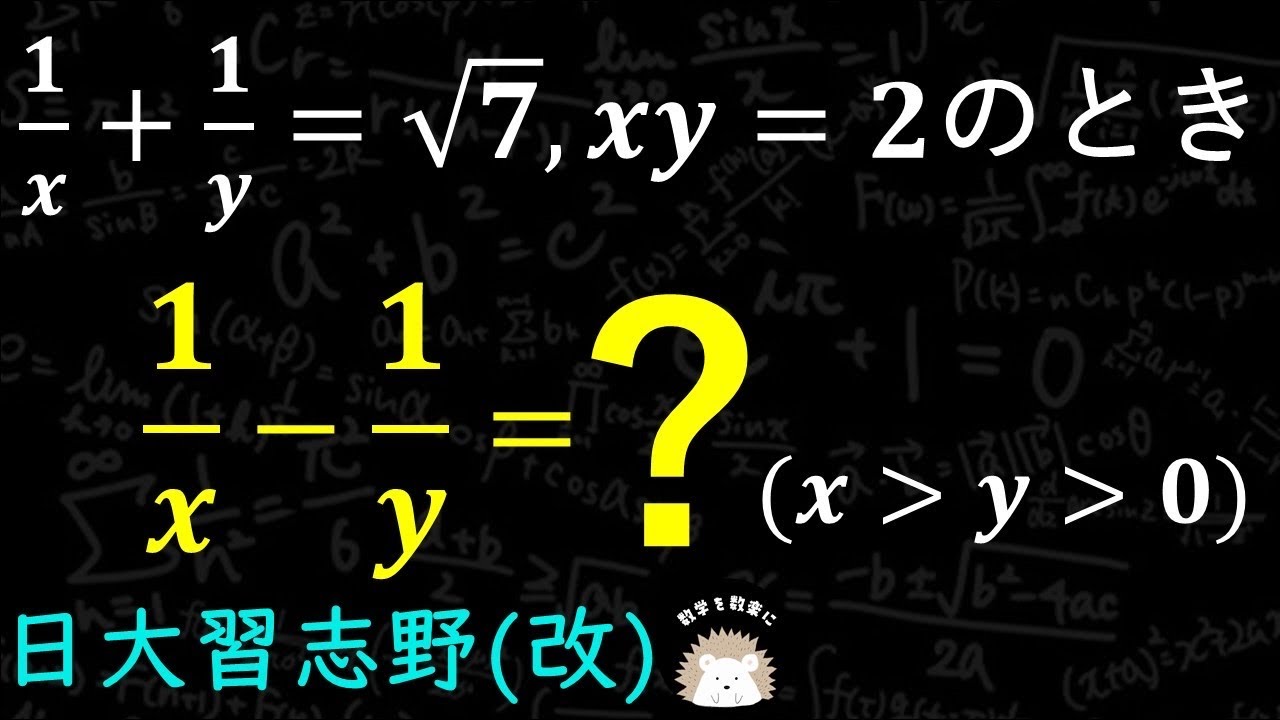
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{x}+\frac{1}{y} = \sqrt 7$ , xy=2のとき
$\frac{1}{x}-\frac{1}{y} = ?$ (x>y>0)
日本大学習志野高等学校
この動画を見る
$\frac{1}{x}+\frac{1}{y} = \sqrt 7$ , xy=2のとき
$\frac{1}{x}-\frac{1}{y} = ?$ (x>y>0)
日本大学習志野高等学校
これ思いつくのすごい

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$x=2-\sqrt{ 3 }$のとき、$x^2-4x-1$の値を求めよ
この動画を見る
$x=2-\sqrt{ 3 }$のとき、$x^2-4x-1$の値を求めよ
