 中3数学
中3数学
 中3数学
中3数学
【5分で内容理解!】二次方程式:大阪教育大学附属高等学校池田校舎~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#大阪教育大学附属高等学校池田校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 大阪教育大学附属高等学校池田校舎
次の式を解きなさい。
$7x^2-42x+58=0$
【解の公式は2種類ある!、公式を忘れても解く!】
この動画を見る
入試問題 大阪教育大学附属高等学校池田校舎
次の式を解きなさい。
$7x^2-42x+58=0$
【解の公式は2種類ある!、公式を忘れても解く!】
【中学数学】因数分解が簡単にできるようになる~数学苦手な人必見~ 1-6【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
超簡単!これを見れば因数分解が簡単にできるようになります!
この動画を見る
超簡単!これを見れば因数分解が簡単にできるようになります!
【実力アップ!】整数:東海高等学校~全国入試問題解法

単元:
#中3数学#高校入試過去問(数学)#東海高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東海高等学校
▭部分を求めよ。
【3桁の正の整数】
各位の数の和が7である。
かつ
百の位の数と一の位の数を入れ替えると、
もとの整数より大きくなる。
このような整数は▭個ある。
この動画を見る
入試問題 東海高等学校
▭部分を求めよ。
【3桁の正の整数】
各位の数の和が7である。
かつ
百の位の数と一の位の数を入れ替えると、
もとの整数より大きくなる。
このような整数は▭個ある。
パックマン

【5分でスッキリ!】文章題:東京工業大学附属科学技術高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#高校入試過去問(数学)#東京工業大学附属科学技術高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
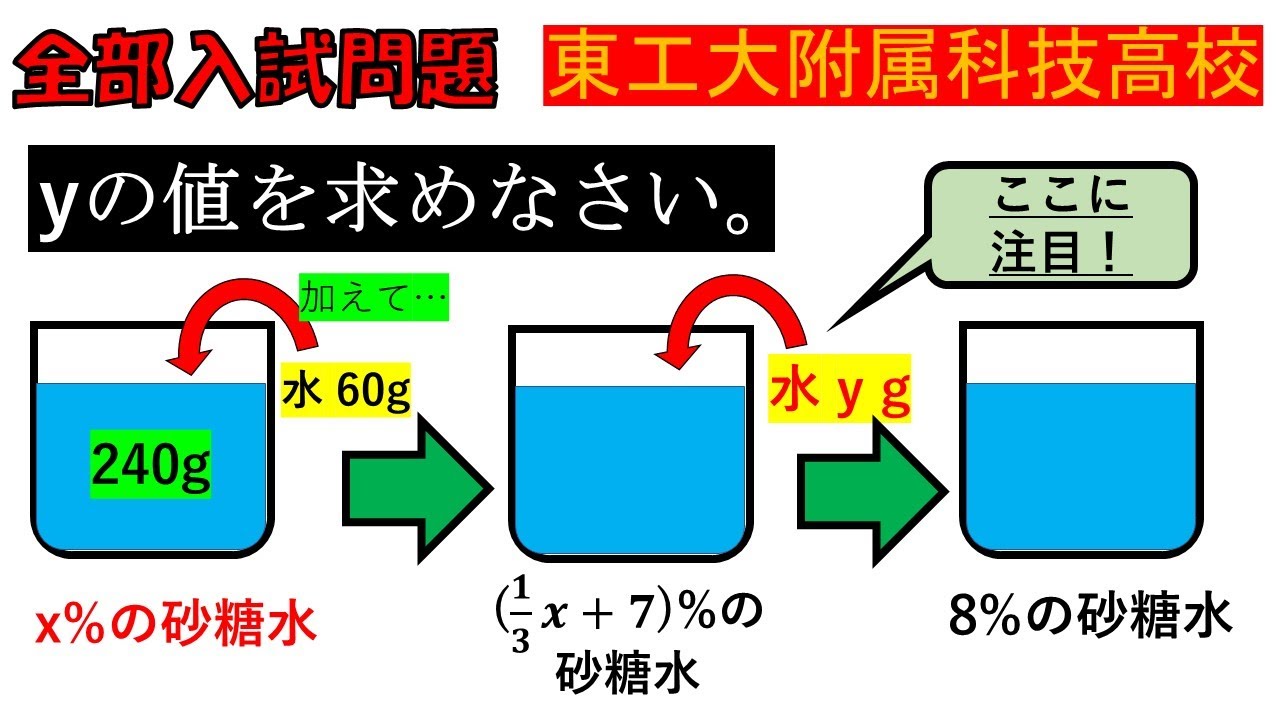
入試問題 東京工業大学附属高等学校
yの値を求めなさい。
※図は動画内参照
この動画を見る
入試問題 東京工業大学附属高等学校
yの値を求めなさい。
※図は動画内参照
【中学数学】数学苦手な人が展開公式を使いこなせるようになる動画 1-5【中3数学】

【雑談】入試問題の作り方《公立編》~全国入試問題解法
単元:
#数学(中学生)#中3数学#その他#高校入試過去問(数学)#その他
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
【雑談】入試問題の作り方《公立編》~全国入試問題解法
受験する高校の過去問は必ず確認しよう!!
この動画を見る
【雑談】入試問題の作り方《公立編》~全国入試問題解法
受験する高校の過去問は必ず確認しよう!!
因数分解 訂正 補足説明あり

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$867ax^5-507axy^2$を因数分解せよ。
白陵高等学校
この動画を見る
$867ax^5-507axy^2$を因数分解せよ。
白陵高等学校
【5分で完全理解!】図形:福岡大学附属大濠高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
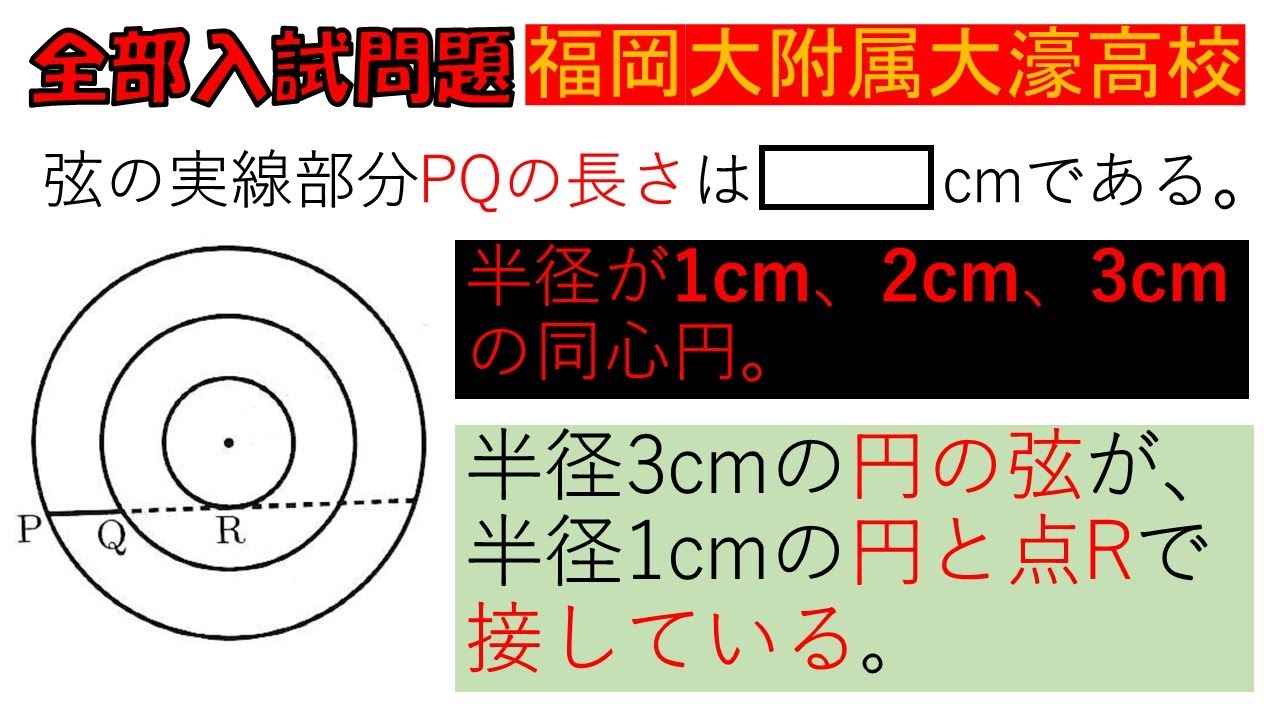
入試問題 福岡大学附属大濠高等学校
▭部分を求めよ。
弦の実線部分$PQ$の長さは▭cmである。
半径が1cm、2cm、3cm の同心円。
半径3cmの円の弦が、 半径1cmの円と点$R$で 接している。
※図は動画内参照
この動画を見る
入試問題 福岡大学附属大濠高等学校
▭部分を求めよ。
弦の実線部分$PQ$の長さは▭cmである。
半径が1cm、2cm、3cm の同心円。
半径3cmの円の弦が、 半径1cmの円と点$R$で 接している。
※図は動画内参照
因数分解 問題がよくできている。。。成城学園

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a{(a+1)(x+1)+3a+3}+(a+1)(x+4)を因数分解
成城学園高等学校
この動画を見る
a{(a+1)(x+1)+3a+3}+(a+1)(x+4)を因数分解
成城学園高等学校
因数分解 白陵高校

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
p(p+1)-q(q+1)を因数分解
白陵高等学校
この動画を見る
p(p+1)-q(q+1)を因数分解
白陵高等学校
因数分解 解き方2通り

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2+(a+1)x+a$を因数分解せよ。
西大和学園高等学校
この動画を見る
$x^2+(a+1)x+a$を因数分解せよ。
西大和学園高等学校
【3分で実力アップ!】二次関数:函館ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 函館ラ・サール高等学校
$a, b$の値を求めなさい。
関数 $y = 2x^2$の
$x$の変域が$-2 \leqq x \leqq a$のとき
$y$の変域が $b \leqq y \leqq 18$である
この動画を見る
入試問題 函館ラ・サール高等学校
$a, b$の値を求めなさい。
関数 $y = 2x^2$の
$x$の変域が$-2 \leqq x \leqq a$のとき
$y$の変域が $b \leqq y \leqq 18$である
大学入試でないよ高校入試だよ

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2-b^2-c^2-2bc$を因数分解せよ。
法政大学高等学校
この動画を見る
$a^2-b^2-c^2-2bc$を因数分解せよ。
法政大学高等学校
【中学数学】三平方の定理:半径3の2つの球AとBが外接している。この2つの球のいずれにも外接するように、半径の等しい6つの球をくっつけたら、6つの球はすべて両隣どうしと外接した。(続きは概要欄で)
単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径3の2つの球AとBが外接している。この2つの球のいずれにも外接するように、半径の等しい6つの球をくっつけたら、6つの球はすべて両隣どうしと外接した。
(1)くっつけた球の半径を求めよう。
(2)6つの球の中心と球Aの中心を結んでできる六角すいの体積を求めよう。
この動画を見る
半径3の2つの球AとBが外接している。この2つの球のいずれにも外接するように、半径の等しい6つの球をくっつけたら、6つの球はすべて両隣どうしと外接した。
(1)くっつけた球の半径を求めよう。
(2)6つの球の中心と球Aの中心を結んでできる六角すいの体積を求めよう。
因数分解 城西大学付属川越

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^4-5x^2+4$を因数分解せよ。
城西大学付属川越高等学校
この動画を見る
$x^4-5x^2+4$を因数分解せよ。
城西大学付属川越高等学校
【連立方程式!?】文字式:東大寺学園高等学校~全国入試問題解法【数楽!?】

単元:
#数学(中学生)#中3数学#高校入試過去問(数学)#東大寺学園高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東大寺学園高等学校
$\sqrt{ 3x }+\sqrt{ 2y }=1$
$\sqrt{ 2x }+\sqrt{ 3y }=\sqrt{ 6 }$
のとき
$x^2-y^2$の値を求めよ。
この動画を見る
入試問題 東大寺学園高等学校
$\sqrt{ 3x }+\sqrt{ 2y }=1$
$\sqrt{ 2x }+\sqrt{ 3y }=\sqrt{ 6 }$
のとき
$x^2-y^2$の値を求めよ。
平方根とは? 三重高校(改)

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
平方根についてのまとめ
・正の数の平方根は$\bbox[red, 5pt, border:]{}$コある。
この$\bbox[red, 5pt, border:]{}$コの数は$\bbox[green, 5pt, border:]{}$が等しく$\bbox[blue, 5pt, border:]{}$が異なる。
・0の平方根は$\bbox[yellow, 5pt, border:]{}$である。
この動画を見る
平方根についてのまとめ
・正の数の平方根は$\bbox[red, 5pt, border:]{}$コある。
この$\bbox[red, 5pt, border:]{}$コの数は$\bbox[green, 5pt, border:]{}$が等しく$\bbox[blue, 5pt, border:]{}$が異なる。
・0の平方根は$\bbox[yellow, 5pt, border:]{}$である。
【悪問!?】文字式:お茶の水女子大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#高校入試過去問(数学)#お茶の水女子大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 お茶の水女子大学附属高等学校
次の式を$c$について解きなさい。
$\displaystyle \frac{a(c-d)}{c+d}+\displaystyle \frac{b(c+d)}{c-d}=a+b$
この動画を見る
入試問題 お茶の水女子大学附属高等学校
次の式を$c$について解きなさい。
$\displaystyle \frac{a(c-d)}{c+d}+\displaystyle \frac{b(c+d)}{c-d}=a+b$
式の値 桐光学園
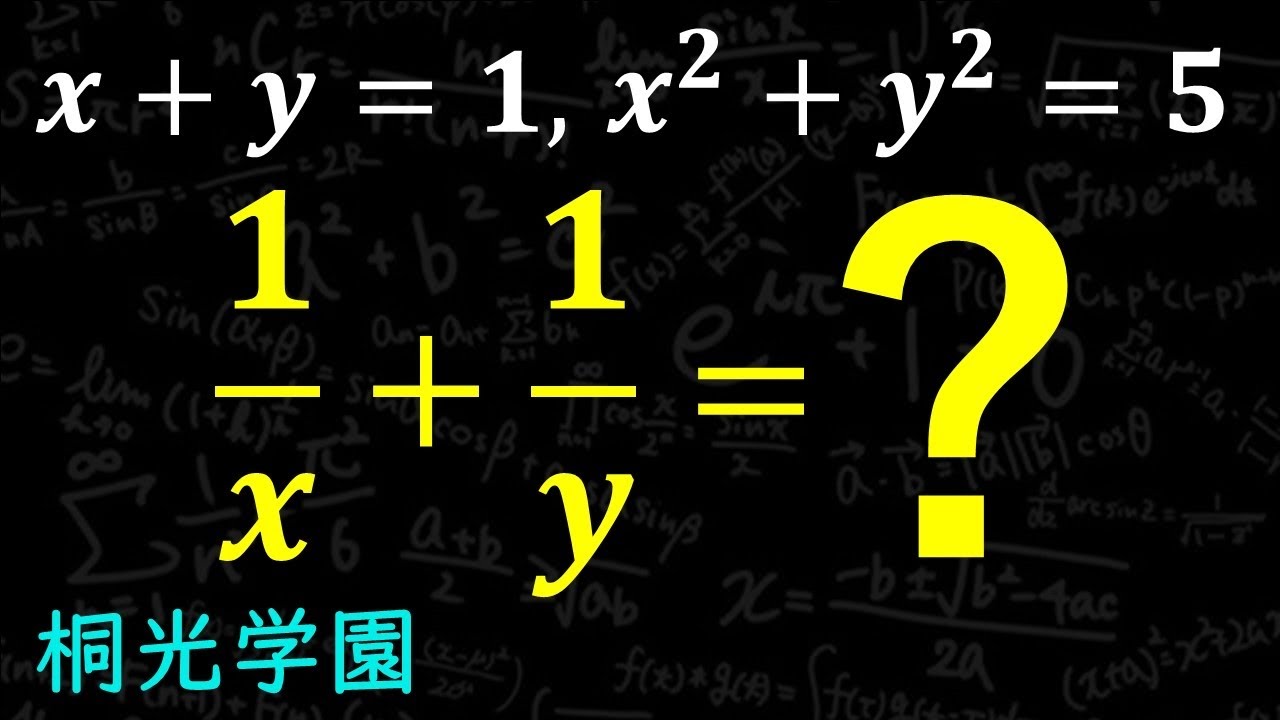
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x+y=1$ , $x^2+y^2=5$
$\frac{1}{x} + \frac{1}{y} = $
この動画を見る
$x+y=1$ , $x^2+y^2=5$
$\frac{1}{x} + \frac{1}{y} = $
式の値 常磐大学高校 A
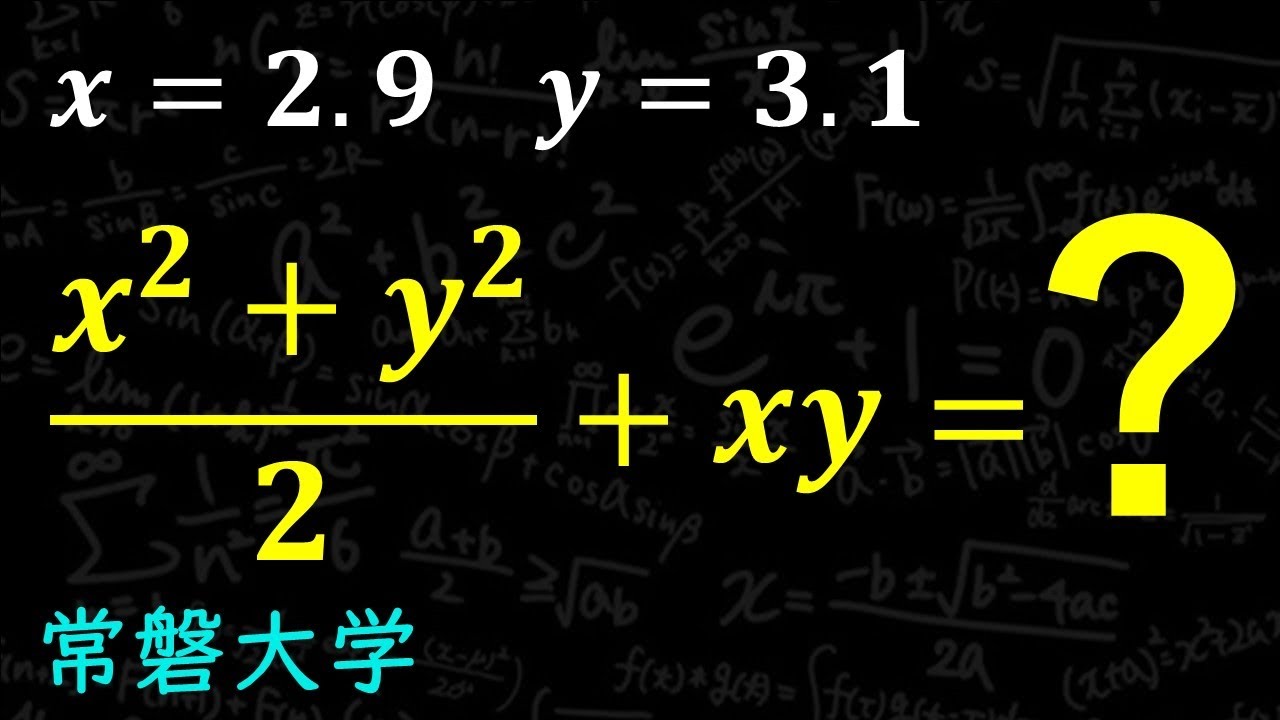
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
x=2.9 , y=3.1のとき
$\frac{x^2+y^2}{2}+xy=$
常磐大学高等学校
この動画を見る
x=2.9 , y=3.1のとき
$\frac{x^2+y^2}{2}+xy=$
常磐大学高等学校
たすきがけの因数分解詳しく解説!!

隣の隣と付き合ってもいい

単元:
#数学(中学生)#中3数学#平方根
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{10} \times \sqrt{22} \times \sqrt{55} =$
この動画を見る
$\sqrt{10} \times \sqrt{22} \times \sqrt{55} =$
【ビリギャル式】因数分解:北海道高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#北海道公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 北海道の高等学校
因数分解せよ。
$2x^2-18$
この動画を見る
入試問題 北海道の高等学校
因数分解せよ。
$2x^2-18$
【5分世界広がる!】連立方程式:渋谷教育学園幕張高等学校~全国入試問題解法【とんとん♪】

単元:
#数学(中学生)#中3数学#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 渋谷教育学園幕張高等学校
連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(3x-2y)^2+8(3x-2y)+16=0 \\
5xy + 15x-2y-6 = 0
\end{array}
\right.
\end{eqnarray}$
この動画を見る
入試問題 渋谷教育学園幕張高等学校
連立方程式を解きなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(3x-2y)^2+8(3x-2y)+16=0 \\
5xy + 15x-2y-6 = 0
\end{array}
\right.
\end{eqnarray}$
頑張って展開!❓😏
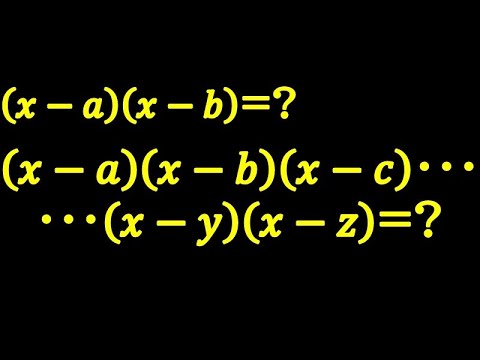
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x-a)(x-b)=?$
$(x-a)(x-b)(x-c) \cdots (x-y)(x-z) $
この動画を見る
$(x-a)(x-b)=?$
$(x-a)(x-b)(x-c) \cdots (x-y)(x-z) $
【朝勉!】朝の因数分解DoJo No.3【因数分解】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
3rd School
問題文全文(内容文):
以下を因数分解してください
$(x^2-3)^2+2(x^2-3)-8$
この動画を見る
以下を因数分解してください
$(x^2-3)^2+2(x^2-3)-8$
【3分間高校入試】平方根:慶応義塾志木高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#慶應義塾志木高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 傾向義塾志木高等学校
$(\sqrt{ 3 }+\sqrt{ 5 })^2$
小数部分を$x$とするとき、
$x^2+14x$の値を求めよ。
この動画を見る
入試問題 傾向義塾志木高等学校
$(\sqrt{ 3 }+\sqrt{ 5 })^2$
小数部分を$x$とするとき、
$x^2+14x$の値を求めよ。
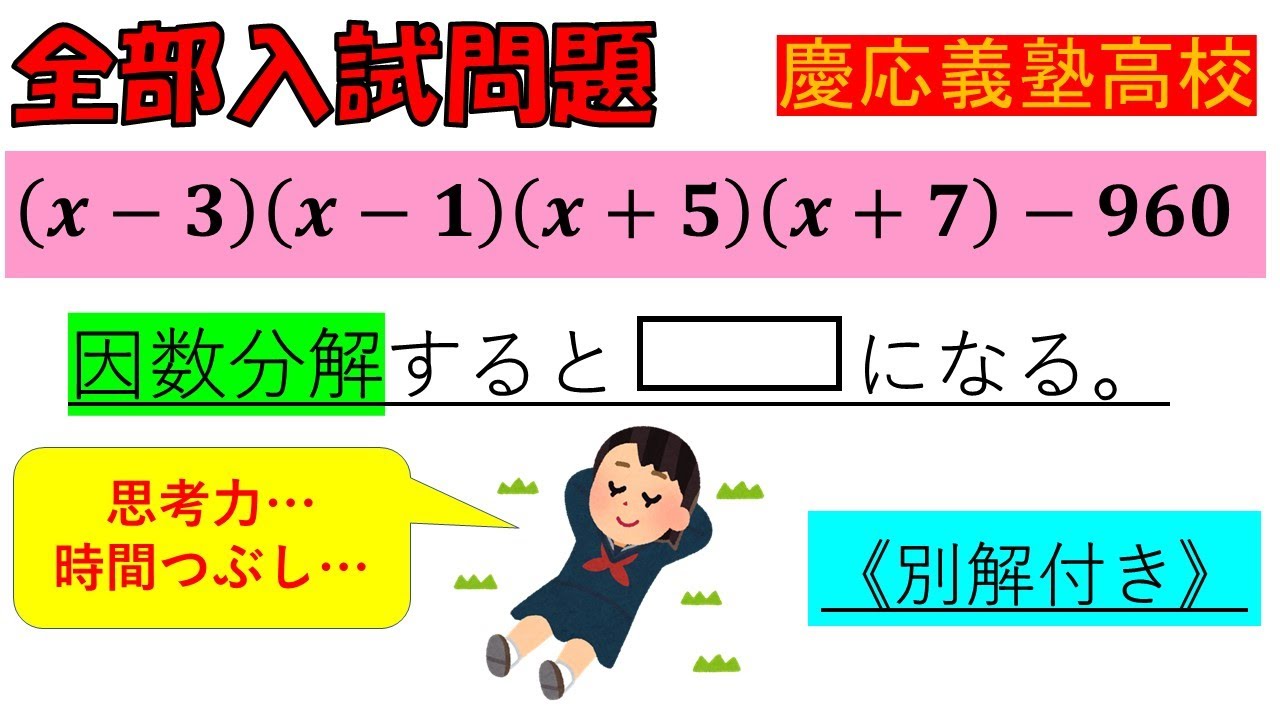
【人生が変わる⁉】因数分解:慶応義塾高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 慶応義塾高等学校
$(x-3)(x-1)(x+5)(x+7)-960$
因数分解すると▭になる。
この動画を見る
入試問題 慶応義塾高等学校
$(x-3)(x-1)(x+5)(x+7)-960$
因数分解すると▭になる。
大学受験の素因数分解

