 中3数学
中3数学
 中3数学
中3数学
円と三平方 中央大附属 C
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
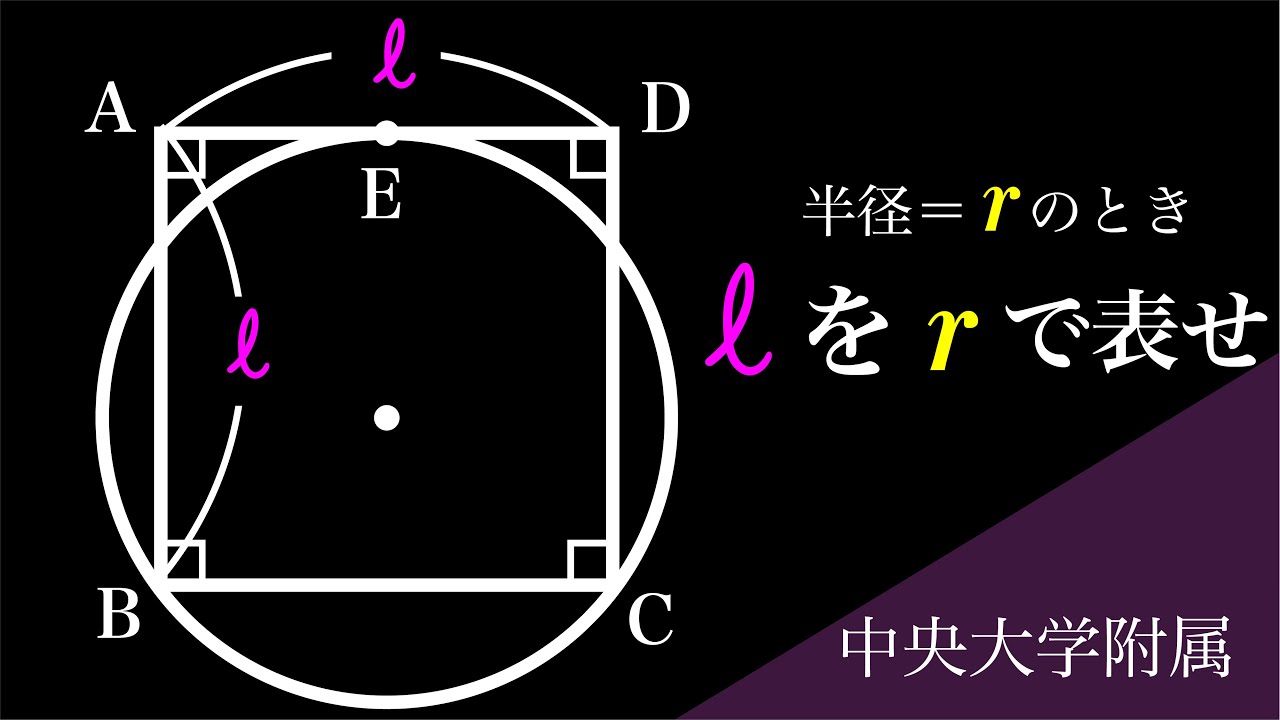
正方形の1辺の長さ=l
半径=r
lをrで表せ
*図は動画内参照
中央大学附属高等学校
この動画を見る
正方形の1辺の長さ=l
半径=r
lをrで表せ
*図は動画内参照
中央大学附属高等学校
因数分解:日本大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#日本大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日本大学第二高等学校
$(x^2+3)^2-16x^2$
を因数分解せよ。
この動画を見る
入試問題 日本大学第二高等学校
$(x^2+3)^2-16x^2$
を因数分解せよ。
【高校受験対策/数学】死守62

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#2次方程式#空間図形#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守62
①$1+(-0.2)\times 2$を計算しなさい。
②方程式$\frac{2x+4}{3}=4$を解きなさい。
③$a=\frac{1}{2},b=3$のとき、 $3(a-2b)-5(3a-b)$の値を 求めなさい。
④$x$についての方程式
$x^2-2ax+3=0$の解の1つが$-1$であるとき、もう1つの解を求めなさい。
⑤1個$a$ kgの品物3個と1個$b$ kgの品物2個の合計の重さは20kg以上である。
この数量の関係を不等式で表しなさい。
⑥右の図のように、側面がすべて長方形の正六角柱がある。
このとき、辺ABとねじれの位置にある辺の数を求めなさい。
⑦家から$a$ m離れた博物館まで、行きは毎分60m、帰りは毎分90mの速さで往復した。
往復の平均の速さは分速( )mである。( )にあてはまる数を求めなさい。
⑧次のア~エのことがらについて、逆が正しいものを1つ選んで記号を書きなさい。
ア 正三角形はすべての内角が等しい三角形である。
イ 長方形は対角線がそれぞれの中点で交わる四角形である。
ウ $x \geqq 5$ならば$x \gt 4$である。
エ $x=1$ならば$x^2=1$である。
⑨右図のように直線$l$上に2点O,Pがある。
点Oを回転の中心として点Pを時計回りに45°回転移動させた点Qを、定規とコンパスを用いて作図しなさい。
ただし作図に用いた線は消さないこと。
この動画を見る
高校受験対策・死守62
①$1+(-0.2)\times 2$を計算しなさい。
②方程式$\frac{2x+4}{3}=4$を解きなさい。
③$a=\frac{1}{2},b=3$のとき、 $3(a-2b)-5(3a-b)$の値を 求めなさい。
④$x$についての方程式
$x^2-2ax+3=0$の解の1つが$-1$であるとき、もう1つの解を求めなさい。
⑤1個$a$ kgの品物3個と1個$b$ kgの品物2個の合計の重さは20kg以上である。
この数量の関係を不等式で表しなさい。
⑥右の図のように、側面がすべて長方形の正六角柱がある。
このとき、辺ABとねじれの位置にある辺の数を求めなさい。
⑦家から$a$ m離れた博物館まで、行きは毎分60m、帰りは毎分90mの速さで往復した。
往復の平均の速さは分速( )mである。( )にあてはまる数を求めなさい。
⑧次のア~エのことがらについて、逆が正しいものを1つ選んで記号を書きなさい。
ア 正三角形はすべての内角が等しい三角形である。
イ 長方形は対角線がそれぞれの中点で交わる四角形である。
ウ $x \geqq 5$ならば$x \gt 4$である。
エ $x=1$ならば$x^2=1$である。
⑨右図のように直線$l$上に2点O,Pがある。
点Oを回転の中心として点Pを時計回りに45°回転移動させた点Qを、定規とコンパスを用いて作図しなさい。
ただし作図に用いた線は消さないこと。
2001を素因数分解せよ 土佐高校

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{676} = ?$
2001を素因数分解せよ。
2011土佐高等学校
この動画を見る
$\sqrt{676} = ?$
2001を素因数分解せよ。
2011土佐高等学校
三平方の定理?いやいや〇〇でしょ A
単元:
#数学(中学生)#中2数学#中3数学#三平方の定理#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
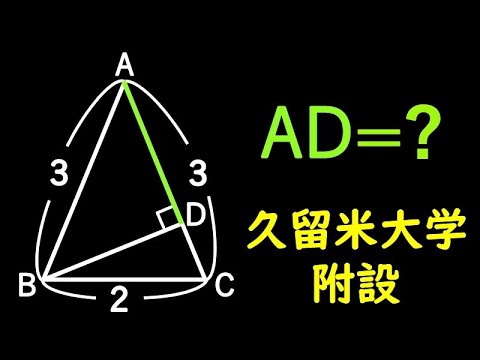
AD=?
*図は動画内参照
久留米大学附設高等学校
この動画を見る
AD=?
*図は動画内参照
久留米大学附設高等学校
因数分解:函館ラ・サール高等学校~全国入試問題解法【メリクリ!】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 函館ラ・サール高等学校
$a^2 – 9b^2 – 4a + 4$
を因数分解しなさい。
この動画を見る
入試問題 函館ラ・サール高等学校
$a^2 – 9b^2 – 4a + 4$
を因数分解しなさい。
整数:函館ラ・サール高等学校~全国入試問題解法【メリクリ!】

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 函館ラ・サール高等学校
$N=2020-\sqrt{ 218x }$
N:整数, x:自然数
Nの絶対値の最小値を求めなさい。
この動画を見る
入試問題 函館ラ・サール高等学校
$N=2020-\sqrt{ 218x }$
N:整数, x:自然数
Nの絶対値の最小値を求めなさい。
【中学数学】関数y=ax²:y=1/2x²とy=ax+bが2点A,Bで交わっている。点A,Bのx座標がそれぞれ-2,3のとき (1)点Aの座標 (2)直線ABの式 (3)△OABの面積 を求めよ。
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
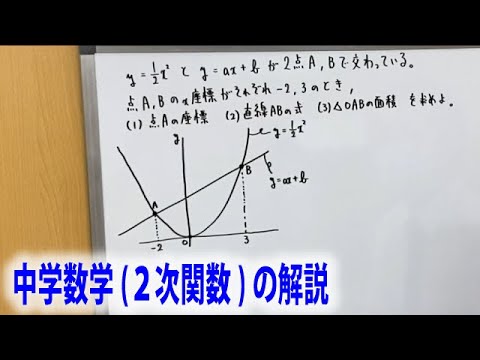
関数$y=ax^2:y=\dfrac{1}{2}x^2$と$y=ax+b$が2点A,Bで交わっている。点A,Bのx座標がそれぞれ-2,3のとき
(1)点Aの座標
(2)直線ABの式
(3)△OABの面積
を求めよ。
この動画を見る
関数$y=ax^2:y=\dfrac{1}{2}x^2$と$y=ax+b$が2点A,Bで交わっている。点A,Bのx座標がそれぞれ-2,3のとき
(1)点Aの座標
(2)直線ABの式
(3)△OABの面積
を求めよ。
反比例と2次方程式 B
単元:
#数学(中学生)#中1数学#中3数学#2次方程式#比例・反比例#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
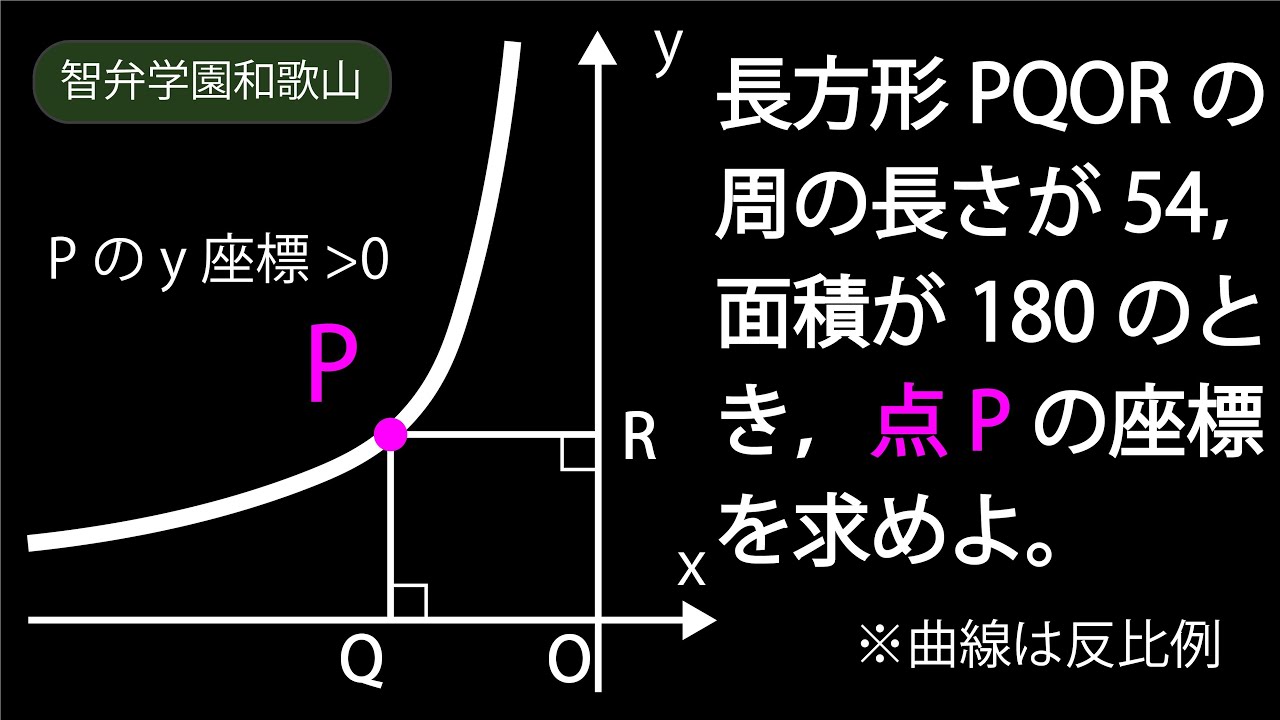
長方形PQORの周の=54、面積=180
点Pの座標は?
(点Pのy座標>0)
*図は動画内参照
智辯学園和歌山高等学校
この動画を見る
長方形PQORの周の=54、面積=180
点Pの座標は?
(点Pのy座標>0)
*図は動画内参照
智辯学園和歌山高等学校
平方根:東京都立新宿高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立新宿高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立新宿高等学校
$x=\displaystyle \frac{5-4\sqrt{ 7 }}{2},y=\displaystyle \frac{5+8\sqrt{ 7 }}{2}$
のとき
→$x^2+2xy+y^2+4x-4y$
の値を求めよ。
この動画を見る
入試問題 東京都立新宿高等学校
$x=\displaystyle \frac{5-4\sqrt{ 7 }}{2},y=\displaystyle \frac{5+8\sqrt{ 7 }}{2}$
のとき
→$x^2+2xy+y^2+4x-4y$
の値を求めよ。
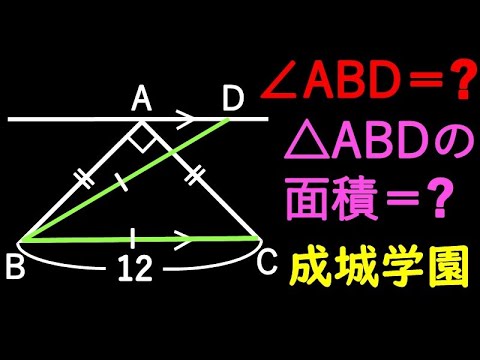
三平方の定理の利用 成城学園
単元:
#数学(中学生)#中3数学#三平方の定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle ABD=?$
$△ABD=?$
*図は動画内参照
成城学園高等学校
この動画を見る
$\angle ABD=?$
$△ABD=?$
*図は動画内参照
成城学園高等学校
二次方程式:東京都立八王子東高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#東京都立八王子東高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立八王子東高等学校
次の問いに答えよ。
2次方程式
$(x + 4)^2−6(x + 4) + 7 = 0 $
を解け。
この動画を見る
入試問題 東京都立八王子東高等学校
次の問いに答えよ。
2次方程式
$(x + 4)^2−6(x + 4) + 7 = 0 $
を解け。
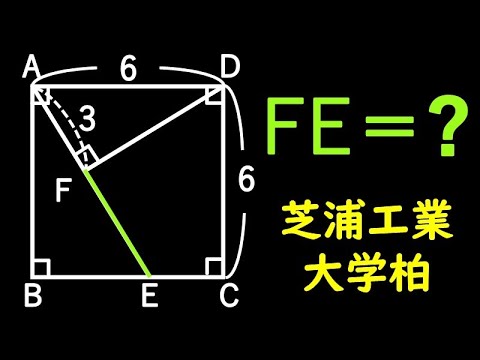
相似 三平方の定理 芝浦工大柏
単元:
#数学(中学生)#中3数学#相似な図形#三平方の定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形ABCDは正方形
EF=?
*図は動画内参照
芝浦工業大学柏高等学校
この動画を見る
四角形ABCDは正方形
EF=?
*図は動画内参照
芝浦工業大学柏高等学校
整数:東京都立立川高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立立川高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立立川高等学校
次の問に答えよ。
$\sqrt{ 2020n }$が整数となるような
$9999$以下の自然数$n$
の個数を求めよ。
この動画を見る
入試問題 東京都立立川高等学校
次の問に答えよ。
$\sqrt{ 2020n }$が整数となるような
$9999$以下の自然数$n$
の個数を求めよ。
【中学数学】2次方程式:図形に関する問題⑪ 右図で、点Pは関数y=1/2x+3上の点で、そのx座標はaである。また、点QはPからx軸に下した垂線とx軸との交点である。a>0のとき、次の問いに答えよ。

単元:
#数学(中学生)#中3数学#2次方程式
教材:
#新中学問題集#新中学問題集(数学)3標準編#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図で、点Pは関数$y=\dfrac{1}{2}x+3$上の点で、そのx座標はaである。また、点QはPからx軸に下した垂線とx軸との交点である。a>0のとき、次の問いに答えよ。
(1)点Pのy座標をaの式で表せ。
(2)△POQの面積が10のとき、点Pの座標を求めよ。
(3)関数$y=\dfrac{1}{2}x+3$とy軸との交点をRとする。△POQの面積が△PORの面積より16大きくなるときの点Pの座標を求めよ。
この動画を見る
右図で、点Pは関数$y=\dfrac{1}{2}x+3$上の点で、そのx座標はaである。また、点QはPからx軸に下した垂線とx軸との交点である。a>0のとき、次の問いに答えよ。
(1)点Pのy座標をaの式で表せ。
(2)△POQの面積が10のとき、点Pの座標を求めよ。
(3)関数$y=\dfrac{1}{2}x+3$とy軸との交点をRとする。△POQの面積が△PORの面積より16大きくなるときの点Pの座標を求めよ。
【中学数学】2次方程式:図形に関する問題⑩ 右図で、点Pはy=-x+2のグラフ上の点で、点AはPO=PAとなるx軸上の点である。点Pのx座標をa(a>0)として、次の問に答えなさい。

単元:
#数学(中学生)#中3数学#2次方程式
教材:
#新中学問題集#新中学問題集(数学)3標準編#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図で、点Pはy=-x+2のグラフ上の点で、点AはPO=PAとなるx軸上の点である。点Pのx座標をa(a>0)として、次の問に答えなさい。
(1)点Pのy座標をaを用いて表そう。
(2)点Aの座標をaを用いて表そう。
(3)△POAの面積が15のとき、点Pの座標を求めよう。
この動画を見る
右図で、点Pはy=-x+2のグラフ上の点で、点AはPO=PAとなるx軸上の点である。点Pのx座標をa(a>0)として、次の問に答えなさい。
(1)点Pのy座標をaを用いて表そう。
(2)点Aの座標をaを用いて表そう。
(3)△POAの面積が15のとき、点Pの座標を求めよう。
図形:東京都立高校入試~全国入試問題解法【とんとん♪】

単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#東京都立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立の高校
図で、
円$O$:線分$AB$が直径
$C, D$は周上の点
$4$点:$A, C, B, D$の順 (一致しない)
$\angle AOC=\angle BDC$
$\angle ABD=34^{ \circ }$
$x$で示した$\angle OCD$の大きさは$口$度である。
$口$部分を求めよ。
※図は動画内参照
この動画を見る
入試問題 東京都立の高校
図で、
円$O$:線分$AB$が直径
$C, D$は周上の点
$4$点:$A, C, B, D$の順 (一致しない)
$\angle AOC=\angle BDC$
$\angle ABD=34^{ \circ }$
$x$で示した$\angle OCD$の大きさは$口$度である。
$口$部分を求めよ。
※図は動画内参照
平方根:日比谷高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日比谷高等学校
次の各問に答えよ。
$(\displaystyle \frac{\sqrt{ 7 }-\sqrt{ 12 }}{2})(\displaystyle \frac{\sqrt{ 7 }}{2}+\sqrt{ 3 })+\sqrt{ 18 }$
を計算せよ。
この動画を見る
入試問題 日比谷高等学校
次の各問に答えよ。
$(\displaystyle \frac{\sqrt{ 7 }-\sqrt{ 12 }}{2})(\displaystyle \frac{\sqrt{ 7 }}{2}+\sqrt{ 3 })+\sqrt{ 18 }$
を計算せよ。
入試に必須!標本調査の利用!意外と難しいので差がつく単元!ぜひマスターしよう!【中3数学】
単元:
#数学(中学生)#中3数学#標本調査
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣Aさんの中学校の生徒数は324人です。Aさんのクラスは36人で、そのうちの10人が昨日の野球中継をテレビで見ていました。
この野球中継は、Aさんの中学校全体では、何人の生徒が見ていたと推測できますか?
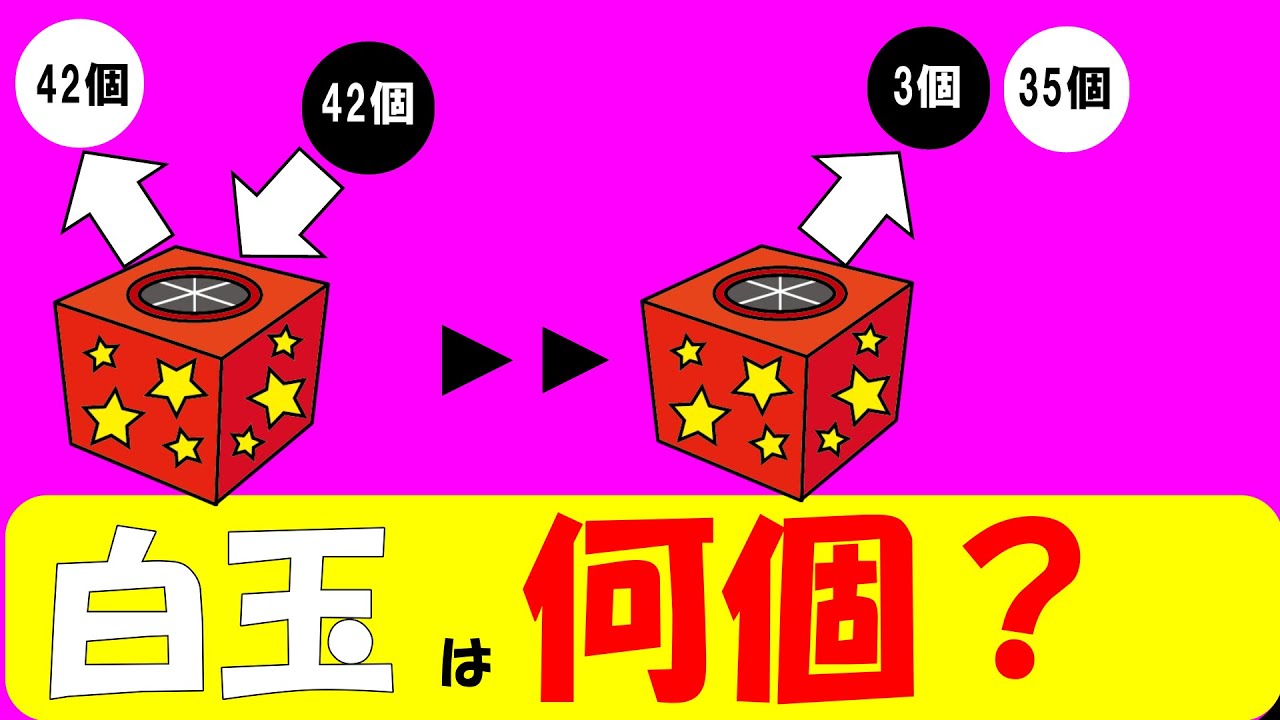
2⃣いくつかの白玉のみが入っている箱があります。その箱から42個の白玉を取り出し、代わりに42個の黒玉を入れてよくかき混ぜました。その後、コップで箱の中の玉をすくうと、黒玉3個と白玉35個が入っていました。はじめに箱の中に入っていた白玉の数は、およそ何個と推測されますか?
この動画を見る
1⃣Aさんの中学校の生徒数は324人です。Aさんのクラスは36人で、そのうちの10人が昨日の野球中継をテレビで見ていました。
この野球中継は、Aさんの中学校全体では、何人の生徒が見ていたと推測できますか?
2⃣いくつかの白玉のみが入っている箱があります。その箱から42個の白玉を取り出し、代わりに42個の黒玉を入れてよくかき混ぜました。その後、コップで箱の中の玉をすくうと、黒玉3個と白玉35個が入っていました。はじめに箱の中に入っていた白玉の数は、およそ何個と推測されますか?
【高校受験対策/数学】死守61

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#平方根#1次関数#2次関数#文字と式#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守6
①$-5+2$を計算しなさい。
➁$6 \times \frac{2a+1}{3}$を計算しなさい。
③$(\sqrt{7}-1)(\sqrt{7}+1)$を計算しなさい。
④連立方程式を解きなさい。
$y=x+6$
$y=-2x+3$
⑤2次方程式$x^2-3x-2=0$を解きなさい。
⑥1辺の長さが$x$ cmの正方形が あります。
この正方形の周の長さを$y$ cmとするとき、$y$を$x$の式で表しなさい。
⑦34人の団体Xと40人の団体Yが博物館に行きます。
この博物館の1人分の入館料は$a$円で、40人以上の団体の入館料は20%引きになります。
このとき、団体Xと団体Yでは入館料の合計はどちらが多くかかりますか。
その理由をことばや式を用いて書きなさい。ただし消費税は考えないものとする。
⑧右の図で、3点、A、B、Cは円$o$の周上にあります。 このとき$\angle x$の大きさを求めなさい。
⑨右下の図のような長方形ABCDの紙を、 頂点Aが頂点Cに重なるように折ったときの折り目の線分を作図によって求めなさい。
ただし、作図には定規とコンパスを用い作図に使った線は消さないでおくこと。
この動画を見る
高校受験対策・死守6
①$-5+2$を計算しなさい。
➁$6 \times \frac{2a+1}{3}$を計算しなさい。
③$(\sqrt{7}-1)(\sqrt{7}+1)$を計算しなさい。
④連立方程式を解きなさい。
$y=x+6$
$y=-2x+3$
⑤2次方程式$x^2-3x-2=0$を解きなさい。
⑥1辺の長さが$x$ cmの正方形が あります。
この正方形の周の長さを$y$ cmとするとき、$y$を$x$の式で表しなさい。
⑦34人の団体Xと40人の団体Yが博物館に行きます。
この博物館の1人分の入館料は$a$円で、40人以上の団体の入館料は20%引きになります。
このとき、団体Xと団体Yでは入館料の合計はどちらが多くかかりますか。
その理由をことばや式を用いて書きなさい。ただし消費税は考えないものとする。
⑧右の図で、3点、A、B、Cは円$o$の周上にあります。 このとき$\angle x$の大きさを求めなさい。
⑨右下の図のような長方形ABCDの紙を、 頂点Aが頂点Cに重なるように折ったときの折り目の線分を作図によって求めなさい。
ただし、作図には定規とコンパスを用い作図に使った線は消さないでおくこと。
入試に必須!標本調査の基礎知識!きちんと対策できていない受験生が多い単元なので、しっかりと身につけよう!【中3数学】

単元:
#数学(中学生)#中3数学#標本調査
指導講師:
こばちゃん塾
問題文全文(内容文):
例1 次の調査は全数調査と標本調査のどちらが適切?
(1)学校の健康診断は__調査
(2)各学校に設置されている火災報知器の定期点検__調査
(3)中学生が1日に視聴しているYouTubeの平均時間は__調査
例2 黒玉と白玉あわせて100個が箱に入っている。この箱から10個の玉を取り出して、黒玉と白玉の数を調査する。この時
・母集団は_____
・標本は_____
・標本の大きさは__である
1⃣次の調査は全数調査と標本調査のどちらが適切でしょう?
(1)5年ごとの国勢調査 (2)暮らしに関する世論調査 (3)テレビ番組の視聴率 (4)高校の入試試験 (5)学校の視力検査 (6)電池の寿命検査
2⃣次の調査の①母集団 ②標本 ③標本の大きさ を答えましょう
A工場で8000個の製品を製造したが、製造過程で500個ごとに製品16個を耐久性テストで検査した。
3⃣学校である標本調査をするため、各クラスから10名を選ぶことになりました。次の問いに答えましょう。
(1)10名の選び方として適切でないものはどれ?
①出席番号から乱数さいで10名を選ぶ ②出席番号から乱数表で10名を選ぶ
③希望者を10名選ぶ ④くじ引きで10名を選ぶ ⑤クラスの専門委員がちょうど10名だったので、その10名を選ぶ
(2)このクラスは乱数表で選ぶことになり、無作為に○をつけた数からはじめ、右へ進めることになりました。下の数は乱数表の一部です。10名を出席番号順に書き出しましょう。ただし、このクラスの生徒数は35名です。
65 95 59 97 84 90 14 79 61 55 56 16 88 87 60 32 15 99 67 43
13 43 00 97 26 16 91 21 32 41 60 22 66 72 17 31 85 33 69 07
この動画を見る
例1 次の調査は全数調査と標本調査のどちらが適切?
(1)学校の健康診断は__調査
(2)各学校に設置されている火災報知器の定期点検__調査
(3)中学生が1日に視聴しているYouTubeの平均時間は__調査
例2 黒玉と白玉あわせて100個が箱に入っている。この箱から10個の玉を取り出して、黒玉と白玉の数を調査する。この時
・母集団は_____
・標本は_____
・標本の大きさは__である
1⃣次の調査は全数調査と標本調査のどちらが適切でしょう?
(1)5年ごとの国勢調査 (2)暮らしに関する世論調査 (3)テレビ番組の視聴率 (4)高校の入試試験 (5)学校の視力検査 (6)電池の寿命検査
2⃣次の調査の①母集団 ②標本 ③標本の大きさ を答えましょう
A工場で8000個の製品を製造したが、製造過程で500個ごとに製品16個を耐久性テストで検査した。
3⃣学校である標本調査をするため、各クラスから10名を選ぶことになりました。次の問いに答えましょう。
(1)10名の選び方として適切でないものはどれ?
①出席番号から乱数さいで10名を選ぶ ②出席番号から乱数表で10名を選ぶ
③希望者を10名選ぶ ④くじ引きで10名を選ぶ ⑤クラスの専門委員がちょうど10名だったので、その10名を選ぶ
(2)このクラスは乱数表で選ぶことになり、無作為に○をつけた数からはじめ、右へ進めることになりました。下の数は乱数表の一部です。10名を出席番号順に書き出しましょう。ただし、このクラスの生徒数は35名です。
65 95 59 97 84 90 14 79 61 55 56 16 88 87 60 32 15 99 67 43
13 43 00 97 26 16 91 21 32 41 60 22 66 72 17 31 85 33 69 07
受験生必見!三平方の定理の定番問題を超分かりやすく解説!!【中3数学】
単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣下の図で、次の長さを求めましょう
(1)BC (2)BD (3)AB (4)AD
2⃣次の図形の面積を求めましょう
(1)
(2)
3⃣3点A(1,3),B(-4,1),C(3,-2)を頂点とする△ABCについて
(1)辺AB,BC,CAの長さは?
(2)△ABCはどんな三角形?
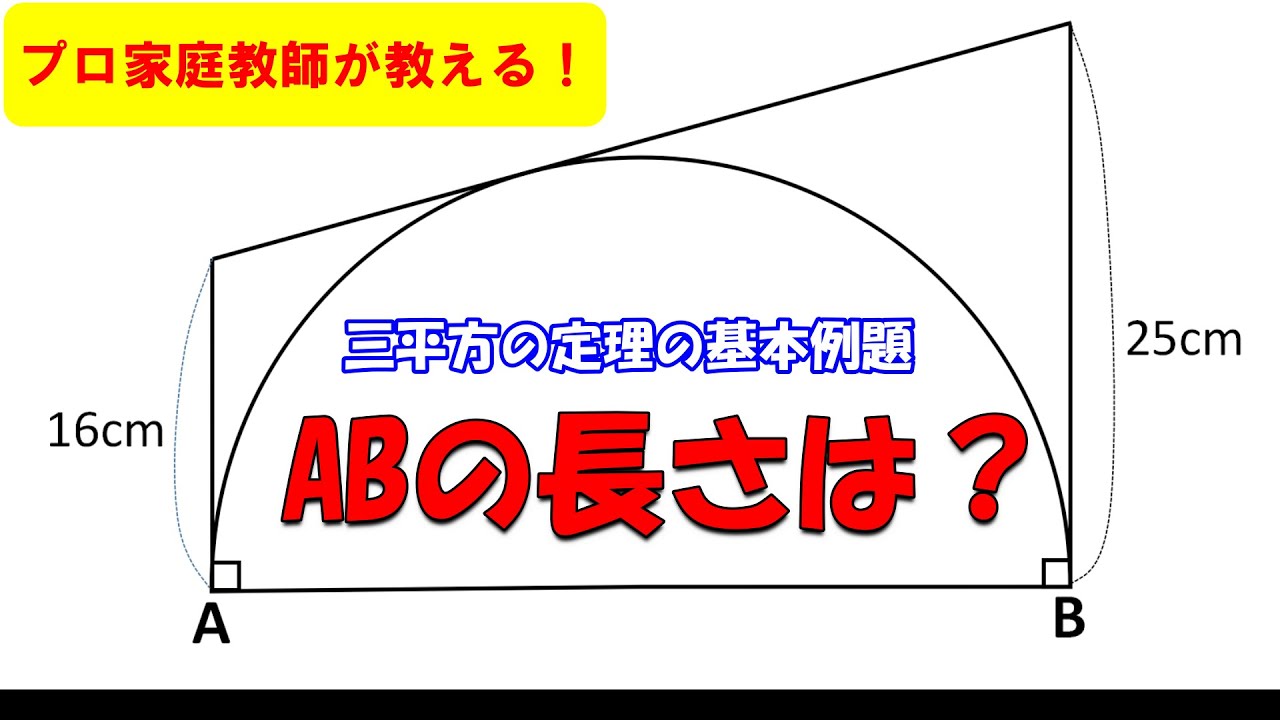
4⃣下の図のABの長さは何㎝?ただし、$\angle PAB = \angle QBA = 90°$
PQは点Cにおける半円Oの接線とする
5⃣右の展開図を組み立ててできる円錐の体積を求めましょう
*図は動画内参照
この動画を見る
1⃣下の図で、次の長さを求めましょう
(1)BC (2)BD (3)AB (4)AD
2⃣次の図形の面積を求めましょう
(1)
(2)
3⃣3点A(1,3),B(-4,1),C(3,-2)を頂点とする△ABCについて
(1)辺AB,BC,CAの長さは?
(2)△ABCはどんな三角形?
4⃣下の図のABの長さは何㎝?ただし、$\angle PAB = \angle QBA = 90°$
PQは点Cにおける半円Oの接線とする
5⃣右の展開図を組み立ててできる円錐の体積を求めましょう
*図は動画内参照
平方根:開成高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#開成高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 開成高等学校
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sqrt{ 3 }x +\sqrt{ 5 } y = \sqrt{ 7 } \\
\displaystyle \frac{ 1 }{\sqrt{ 3 }}+\displaystyle \frac{ 1 }{\sqrt{ 5 }} = \displaystyle \frac{ 1 }{\sqrt{ 7 }}
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
この動画を見る
入試問題 開成高等学校
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sqrt{ 3 }x +\sqrt{ 5 } y = \sqrt{ 7 } \\
\displaystyle \frac{ 1 }{\sqrt{ 3 }}+\displaystyle \frac{ 1 }{\sqrt{ 5 }} = \displaystyle \frac{ 1 }{\sqrt{ 7 }}
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
【エナドリ】平方根:埼玉県高校入試~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#埼玉県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 埼玉県の高校
下の問に答えよ。
$x=2+\sqrt{ 3 }$
$y=2-\sqrt{ 3 }$
のとき
→$(1+\displaystyle \frac{ 1 }{x})(1+\displaystyle \frac{ 1 }{y})$
の値を求めよ。
この動画を見る
入試問題 埼玉県の高校
下の問に答えよ。
$x=2+\sqrt{ 3 }$
$y=2-\sqrt{ 3 }$
のとき
→$(1+\displaystyle \frac{ 1 }{x})(1+\displaystyle \frac{ 1 }{y})$
の値を求めよ。
【チャレンジ】24問耐久計算問題~全国入試問題解法【数楽!】

単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
高校入試の問題から小問集合
(1)$7+(-5)$
(2)$-4 \div \displaystyle \frac{ 1 }{9}+8$
(3)$\sqrt{ 6 } \times \sqrt{ 2 }-\sqrt{ 3 }$
(4)$-8 +6$
(5)$(-0.5) \div \displaystyle \frac{ 2 }{7}$
(6)$ a+3ℓ-2$ ,$- a-ℓ+4 $
(7)$\sqrt{ 3 }-\displaystyle \frac{ 9 }{\sqrt{ 3 }}-\sqrt{ 12 }$
(8)$-2-5$
(9)$8(\displaystyle \frac{ 3 }{4}a+1) $
(10)$( 3-\sqrt{ 2 }^2)$
(11)$-5+14$
(12)$-6 \div 3^2 \times 2 $
(13)$ 4(x+2y)-(-x+y)$
(14)$\displaystyle \frac{ 1 }{\sqrt{ 2 }}(\sqrt{ 6 }+\sqrt{ 24 })$
(15)$\displaystyle \frac{ 5 }{6} \times (-0.4)$
(16)$2(3a-2ℓ)-3(2a-ℓ) $
(17)$ 6:8=x:20$
(18)$\sqrt{ 24 }-\displaystyle \frac{ 18 }{\sqrt{ 6 }}$
(19)$4 \times (-3)$
(20)$\displaystyle \frac{ 4 }{3}-2 $
(21)$ 3.8 \div 4$
(22)$\sqrt{ 2 } \times 2\sqrt{ 6 }$
(23)$(-5a)^2$
(24)$2(x+1)-(1-x)$
この動画を見る
高校入試の問題から小問集合
(1)$7+(-5)$
(2)$-4 \div \displaystyle \frac{ 1 }{9}+8$
(3)$\sqrt{ 6 } \times \sqrt{ 2 }-\sqrt{ 3 }$
(4)$-8 +6$
(5)$(-0.5) \div \displaystyle \frac{ 2 }{7}$
(6)$ a+3ℓ-2$ ,$- a-ℓ+4 $
(7)$\sqrt{ 3 }-\displaystyle \frac{ 9 }{\sqrt{ 3 }}-\sqrt{ 12 }$
(8)$-2-5$
(9)$8(\displaystyle \frac{ 3 }{4}a+1) $
(10)$( 3-\sqrt{ 2 }^2)$
(11)$-5+14$
(12)$-6 \div 3^2 \times 2 $
(13)$ 4(x+2y)-(-x+y)$
(14)$\displaystyle \frac{ 1 }{\sqrt{ 2 }}(\sqrt{ 6 }+\sqrt{ 24 })$
(15)$\displaystyle \frac{ 5 }{6} \times (-0.4)$
(16)$2(3a-2ℓ)-3(2a-ℓ) $
(17)$ 6:8=x:20$
(18)$\sqrt{ 24 }-\displaystyle \frac{ 18 }{\sqrt{ 6 }}$
(19)$4 \times (-3)$
(20)$\displaystyle \frac{ 4 }{3}-2 $
(21)$ 3.8 \div 4$
(22)$\sqrt{ 2 } \times 2\sqrt{ 6 }$
(23)$(-5a)^2$
(24)$2(x+1)-(1-x)$
【中3数学】受験生必見!三平方の空間図形への利用を超分かりやすく解説!!

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣次の立体の対角線の長さを求めましょう
(1)1辺が4㎝の立方体
(2)3辺の長さが3㎝、4㎝、12㎝の直方体
2⃣下の展開図について答えましょう
(1)この円錐の高さは何㎝?
(2)この円錐の体積は何㎠?
3⃣右の正四角錐について答えましょう
(1)ACは何㎝?
(2)高さOHは何㎝?
(3)この立体の体積は何㎤?
(4)この立体の側面積は何㎠?
*図は動画内参照
この動画を見る
1⃣次の立体の対角線の長さを求めましょう
(1)1辺が4㎝の立方体
(2)3辺の長さが3㎝、4㎝、12㎝の直方体
2⃣下の展開図について答えましょう
(1)この円錐の高さは何㎝?
(2)この円錐の体積は何㎠?
3⃣右の正四角錐について答えましょう
(1)ACは何㎝?
(2)高さOHは何㎝?
(3)この立体の体積は何㎤?
(4)この立体の側面積は何㎠?
*図は動画内参照
【中3数学】受験生必見!三平方の平面図形への利用を超分かりやすく解説!!

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣下の図について次の問いに答えましょう
(1)高さAHは何㎝?
(2)△ABCの面積は?
2⃣次の問いに答えましょう
(1)対角線の長さが8㎝の正方形の1辺の長さは何㎝?
(2)1辺の長さが4㎝の正三角形の高さは何㎝?また面積は何㎠?
3⃣xの値を求めましょう
(1)(2)(3)
4⃣次の座標をもつ2点間の距離を求めよう
(1)A(1,2),B(7,10)
(2)A(-3,-5),B(2,3)
(3)A(5,-2),B(-1,4)
(4)A(-3,-6),B(-6,-9)
*図は動画内参照
この動画を見る
1⃣下の図について次の問いに答えましょう
(1)高さAHは何㎝?
(2)△ABCの面積は?
2⃣次の問いに答えましょう
(1)対角線の長さが8㎝の正方形の1辺の長さは何㎝?
(2)1辺の長さが4㎝の正三角形の高さは何㎝?また面積は何㎠?
3⃣xの値を求めましょう
(1)(2)(3)
4⃣次の座標をもつ2点間の距離を求めよう
(1)A(1,2),B(7,10)
(2)A(-3,-5),B(2,3)
(3)A(5,-2),B(-1,4)
(4)A(-3,-6),B(-6,-9)
*図は動画内参照
【中3数学】受験生必見!三平方の定理を超分かりやすく解説!!

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
こばちゃん塾
問題文全文(内容文):
1⃣下の図で、xの値を求めよう。
(1)(2)(3)(4)
2⃣次の長さを3辺とする三角形のうち、直角三角形はどれ?
㋐6㎝、8㎝、10㎝ ㋑7㎝、8㎝、12㎝ ㋒3㎝、4㎝、$\sqrt{7}$㎝
㋓$\sqrt{2}$㎝、$\sqrt{3}$㎝、2㎝
*図は動画内参照
この動画を見る
1⃣下の図で、xの値を求めよう。
(1)(2)(3)(4)
2⃣次の長さを3辺とする三角形のうち、直角三角形はどれ?
㋐6㎝、8㎝、10㎝ ㋑7㎝、8㎝、12㎝ ㋒3㎝、4㎝、$\sqrt{7}$㎝
㋓$\sqrt{2}$㎝、$\sqrt{3}$㎝、2㎝
*図は動画内参照
【大学入試の簡易版!】二次方程式:お茶の水女子大学付属高等学校②~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#お茶の水女子大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 お茶の水女子大学付属高等学校
$x$についての$2$次方程式
$x^2 + (a + 2)x + a^2+2a − 1 = 0$
解の$1$つが$a$である。
$a$の値を求めよ。
(ただし、$a \gt 0$)
この動画を見る
入試問題 お茶の水女子大学付属高等学校
$x$についての$2$次方程式
$x^2 + (a + 2)x + a^2+2a − 1 = 0$
解の$1$つが$a$である。
$a$の値を求めよ。
(ただし、$a \gt 0$)
平方根:代表的な無理数の暗記法~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
平方根:代表的な無理数の暗記法~全国入試問題解法
$\sqrt{ 2 } = 1.41421356$ 一夜一夜に人見ごろ
$\sqrt{ 3 } = 1.7320508$ ...人なみにおごれや
$\sqrt{ 5 } = 2.2360679$ 富士山ろくオウム鳴く
$\sqrt{ 6 } = 2 2.4494897$... 二夜シクシク
$\sqrt{ 7 } = 2 2.6457513$... 変に虫いないさ
$\sqrt{ 8 } = 2 2.828427$… ニヤニヤ呼ぶな
$\sqrt{ 10 } = 3 3,1622776.$……… 人丸は三色に並ぶや
この動画を見る
平方根:代表的な無理数の暗記法~全国入試問題解法
$\sqrt{ 2 } = 1.41421356$ 一夜一夜に人見ごろ
$\sqrt{ 3 } = 1.7320508$ ...人なみにおごれや
$\sqrt{ 5 } = 2.2360679$ 富士山ろくオウム鳴く
$\sqrt{ 6 } = 2 2.4494897$... 二夜シクシク
$\sqrt{ 7 } = 2 2.6457513$... 変に虫いないさ
$\sqrt{ 8 } = 2 2.828427$… ニヤニヤ呼ぶな
$\sqrt{ 10 } = 3 3,1622776.$……… 人丸は三色に並ぶや
