 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
角度を求める A A A (清風)
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
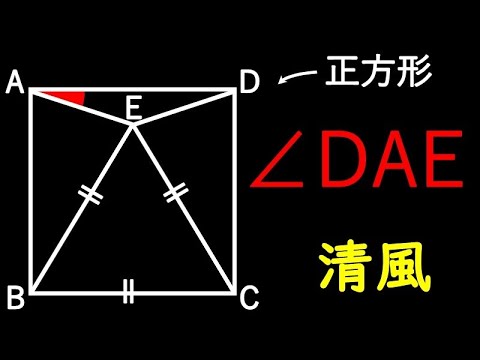
四角形ABCDは正方形
$\angle DAE=?$
*図は動画内参照
横浜清風高等学校
この動画を見る
四角形ABCDは正方形
$\angle DAE=?$
*図は動画内参照
横浜清風高等学校
二次関数:関西学院高等部~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#関西学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 関西学院高等部
放物線$y=x^2$
直線$y = ax + a(a \gt 0)$
$2$点$A$と$B$で交わる。
点$P:y=a$のとき、$x=a$
$\triangle OAB$の面積を求めよ。
※図は動画内参照
この動画を見る
入試問題 関西学院高等部
放物線$y=x^2$
直線$y = ax + a(a \gt 0)$
$2$点$A$と$B$で交わる。
点$P:y=a$のとき、$x=a$
$\triangle OAB$の面積を求めよ。
※図は動画内参照
【高校受験対策/数学】死守68

単元:
#算数(中学受験)#数学(中学生)#中3数学#2次方程式#平面図形#平面図形その他#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$5+(-3)×2$を計算しなさい。
②$3xy^2÷ (-2x^2y)×4y$を計算しなさい。
③$a=\sqrt{6}$のとき$a(a+2)-2(a+2)$の値を求めなさい。
④二次方程式$x^2+6x-16=0$を解きなさい。
⑤$\sqrt{45}+\sqrt{5}-\sqrt{20}$を計算しなさい。
⑥定価1500円のTシャツを$a$割引で買ったときの代金を、$a$を使った式で表しなさい。
ただし消費税は考えないものとする。
⑦右の図は、ある中学校3年生男子50人の50m走の記録をヒストグラムに表したも のである。
図において、例えば6.0から 6.5の区間は、6.0秒以上6.5秒未満の階級を表したものである。
このとき最頻値を求めなさい。
⑧右の図のように、$\angle B=90°$である直角三角形$ABC$がある。
$DA=DB=BC$となるような点$D$が辺$AC$上にあるとき、$\angle x$の大きさを求めなさい。
③右の図のような$\triangle ABC$がある。
線分$AC$上にあり、$\angle PAB=\angle PBA$となる点$P$を作図によって求め、$P$の記号をつけなさい。
ただし作図に用いた線は残しておくこと。
この動画を見る
①$5+(-3)×2$を計算しなさい。
②$3xy^2÷ (-2x^2y)×4y$を計算しなさい。
③$a=\sqrt{6}$のとき$a(a+2)-2(a+2)$の値を求めなさい。
④二次方程式$x^2+6x-16=0$を解きなさい。
⑤$\sqrt{45}+\sqrt{5}-\sqrt{20}$を計算しなさい。
⑥定価1500円のTシャツを$a$割引で買ったときの代金を、$a$を使った式で表しなさい。
ただし消費税は考えないものとする。
⑦右の図は、ある中学校3年生男子50人の50m走の記録をヒストグラムに表したも のである。
図において、例えば6.0から 6.5の区間は、6.0秒以上6.5秒未満の階級を表したものである。
このとき最頻値を求めなさい。
⑧右の図のように、$\angle B=90°$である直角三角形$ABC$がある。
$DA=DB=BC$となるような点$D$が辺$AC$上にあるとき、$\angle x$の大きさを求めなさい。
③右の図のような$\triangle ABC$がある。
線分$AC$上にあり、$\angle PAB=\angle PBA$となる点$P$を作図によって求め、$P$の記号をつけなさい。
ただし作図に用いた線は残しておくこと。
三平方の定理:証明《後編》~全国入試問題解法【とんとん♪】

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
三平方の定理:証明《後編》
$a^2+c^2=c^2$
直角三角形の直角を挟む2辺の長さを$c$とする。
※図は動画内参照
この動画を見る
三平方の定理:証明《後編》
$a^2+c^2=c^2$
直角三角形の直角を挟む2辺の長さを$c$とする。
※図は動画内参照
三平方の定理:証明《前編》~全国入試問題解法【数楽!】

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
三平方の定理:証明《前編》
$a^2+b^2=c^2$
直角△の直角を挟む 2辺の長さをCとする。
※図は動画内参照
この動画を見る
三平方の定理:証明《前編》
$a^2+b^2=c^2$
直角△の直角を挟む 2辺の長さをCとする。
※図は動画内参照
共通テスト2021年詳しい解説〜共通テスト2021年2B第3問〜統計

単元:
#数学(中学生)#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#統計的な推測#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large第3問}$
Q高校の校長先生は、ある日、新聞で高校生の読書に関する記事を読んだ。そこで、
Q高校の生徒全員を対象に、直前の1週間の読書時間に関して、100人の
生徒を無作為に抽出して調査を行った。その結果、100人の生徒のうち、この
1週間に全く読書をしなかった生徒が36人であり、100人の生徒のこの1週間の
読書時間(分)の平均値は204であった。Q高校の生徒全員のこの1週間の読書時間
の母平均を$m$, 母標準偏差を150とする。
(1)全く読書をしなかった生徒の母比率を0.5とする。このとき、100人の無作為標本の
うちで全く読書をしなかった生徒の数を表す確率変数をXとすると、$X$は$\boxed{\boxed{\ \ ア\ \ }}$
に従う。また、Xの平均(期待値)は$\boxed{\ \ イウ\ \ }$、標準偏差は$\boxed{\ \ エ\ \ }$である。
$\boxed{\boxed{\ \ ア\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪正規分布$N(0,1)$
①二項分布$B(0,1)$
②正規分布$N(100,0.5)$
③二項分布$B(100,0.5)$
④正規分布$N(100,36)$
⑤二項分布$B(100,36)$
(2)標本の大きさ100は十分に大きいので、100人のうち全く読書をしなかった生徒
の数は近似的に正規分布に従う。
全く読書をしなかった生徒の母比率を0.5とするとき、全く読書をしなかった生徒
が36人以下となる確率を$p_5$とおく。$p_5$の近似値を求めると、$p_5=\boxed{\boxed{\ \ オ\ \ }}$である。
また、全く読書をしなかった生徒の母比率を0.4とするとき、全く読書をしなかった
生徒が36人以下となる確率を$p_4$とおくと、$\boxed{\boxed{\ \ カ\ \ }}$である。
$\boxed{\boxed{\ \ オ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪$0.001$
①$0.003$
②$0.026$
③$0.050$
④$0.133$
⑤$0.497$
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪$p_4 \lt p_5$
①$p_4 = p_5$
②$p_4 \gt p_5$
(3)1週間の読書時間の母平均$m$に対する信頼度95%の信頼区間を
$C_1 \leqq m \leqq C_2$とする。標本の大きさ100は十分大きいことと、1週間
の読書時間の標本平均が204、母標準偏差が150であることを用いると、
$C_1+C_2=\boxed{\ \ キクケ\ \ }$、$C_2-C_1=\boxed{\ \ コサ\ \ }.\boxed{\ \ シ\ \ }$であることがわかる。
また、母平均$m$と$C_1,C_2$については$\boxed{\boxed{\ \ ス\ \ }}$。
$\boxed{\boxed{\ \ ス\ \ }}$の解答群
⓪$C_1 \leqq m \leqq C_2$が必ず成り立つ
①$m \leqq C_2$は必ず成り立つが、$C_1 \leqq m$が成り立つとは限らない
②$C_1 \leqq m$は必ず成り立つが、$m \leqq C_2$が成り立つとは限らない
③$C_1 \leqq m$も$m \leqq C_2$も成り立つとは限らない
(4)Q高校の図書委員長も、校長先生と同じ新聞記事を読んだため、校長先生が
調査をしていることを知らずに、図書委員会として校長先生と同様の調査を
独自に行った。ただし、調査期間は校長先生による調査と同じ直前の1週間であり、
対象をQ高校の生徒全員として100人の生徒を無作為に抽出した。その調査における
全く読書をしなかった生徒の数を$n$とする。
校長先生の調査結果によると全く読書をしなかった生徒は36人であり、
$\boxed{\boxed{\ \ セ\ \ }}$。
$\boxed{\boxed{\ \ セ\ \ }}$の解答群
⓪$n$は必ず36に等しい
①$n$は必ず36未満である
②$n$は必ず36より大きい
③$n$と36との大小はわからない
(5)(4)の図書委員会が行った調査結果による母平均$m$に対する信頼度95%の
信頼区間を$D_1 \leqq m \leqq D_2$、校長先生が行った調査結果による母平均$m$に対す
る信頼度95%の信頼区間を(3)の$C_1 \leqq m \leqq C_2$とする。ただし、母集団は同一
であり、1週間の読書時間の母標準偏差は150とする。
このとき、次の⓪~⑤のうち、正しいものは$\boxed{\boxed{\ \ ソ\ \ }}と\boxed{\boxed{\ \ タ\ \ }}$である。
$\boxed{\boxed{\ \ ソ\ \ }}$, $\boxed{\boxed{\ \ タ\ \ }}$の解答群(解答の順序は問わない。)
⓪$C_1=D_1とC_2=D_2$が必ず成り立つ。
①$C_1 \lt D_2$または$D_1 \lt C_2$のどちらか一方のみが成り立つ。
②$D_2 \lt C_1$または$C_2 \lt D_1$となる場合もある。
③$C_2-C_1 \gt D_2-D_1$が必ず成り立つ。
④$C_2-C_1 = D_2-D_1$が必ず成り立つ。
⑤$C_2-C_1 \lt D_2-D_1$が必ず成り立つ。
2021共通テスト過去問
この動画を見る
${\large第3問}$
Q高校の校長先生は、ある日、新聞で高校生の読書に関する記事を読んだ。そこで、
Q高校の生徒全員を対象に、直前の1週間の読書時間に関して、100人の
生徒を無作為に抽出して調査を行った。その結果、100人の生徒のうち、この
1週間に全く読書をしなかった生徒が36人であり、100人の生徒のこの1週間の
読書時間(分)の平均値は204であった。Q高校の生徒全員のこの1週間の読書時間
の母平均を$m$, 母標準偏差を150とする。
(1)全く読書をしなかった生徒の母比率を0.5とする。このとき、100人の無作為標本の
うちで全く読書をしなかった生徒の数を表す確率変数をXとすると、$X$は$\boxed{\boxed{\ \ ア\ \ }}$
に従う。また、Xの平均(期待値)は$\boxed{\ \ イウ\ \ }$、標準偏差は$\boxed{\ \ エ\ \ }$である。
$\boxed{\boxed{\ \ ア\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪正規分布$N(0,1)$
①二項分布$B(0,1)$
②正規分布$N(100,0.5)$
③二項分布$B(100,0.5)$
④正規分布$N(100,36)$
⑤二項分布$B(100,36)$
(2)標本の大きさ100は十分に大きいので、100人のうち全く読書をしなかった生徒
の数は近似的に正規分布に従う。
全く読書をしなかった生徒の母比率を0.5とするとき、全く読書をしなかった生徒
が36人以下となる確率を$p_5$とおく。$p_5$の近似値を求めると、$p_5=\boxed{\boxed{\ \ オ\ \ }}$である。
また、全く読書をしなかった生徒の母比率を0.4とするとき、全く読書をしなかった
生徒が36人以下となる確率を$p_4$とおくと、$\boxed{\boxed{\ \ カ\ \ }}$である。
$\boxed{\boxed{\ \ オ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪$0.001$
①$0.003$
②$0.026$
③$0.050$
④$0.133$
⑤$0.497$
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪$p_4 \lt p_5$
①$p_4 = p_5$
②$p_4 \gt p_5$
(3)1週間の読書時間の母平均$m$に対する信頼度95%の信頼区間を
$C_1 \leqq m \leqq C_2$とする。標本の大きさ100は十分大きいことと、1週間
の読書時間の標本平均が204、母標準偏差が150であることを用いると、
$C_1+C_2=\boxed{\ \ キクケ\ \ }$、$C_2-C_1=\boxed{\ \ コサ\ \ }.\boxed{\ \ シ\ \ }$であることがわかる。
また、母平均$m$と$C_1,C_2$については$\boxed{\boxed{\ \ ス\ \ }}$。
$\boxed{\boxed{\ \ ス\ \ }}$の解答群
⓪$C_1 \leqq m \leqq C_2$が必ず成り立つ
①$m \leqq C_2$は必ず成り立つが、$C_1 \leqq m$が成り立つとは限らない
②$C_1 \leqq m$は必ず成り立つが、$m \leqq C_2$が成り立つとは限らない
③$C_1 \leqq m$も$m \leqq C_2$も成り立つとは限らない
(4)Q高校の図書委員長も、校長先生と同じ新聞記事を読んだため、校長先生が
調査をしていることを知らずに、図書委員会として校長先生と同様の調査を
独自に行った。ただし、調査期間は校長先生による調査と同じ直前の1週間であり、
対象をQ高校の生徒全員として100人の生徒を無作為に抽出した。その調査における
全く読書をしなかった生徒の数を$n$とする。
校長先生の調査結果によると全く読書をしなかった生徒は36人であり、
$\boxed{\boxed{\ \ セ\ \ }}$。
$\boxed{\boxed{\ \ セ\ \ }}$の解答群
⓪$n$は必ず36に等しい
①$n$は必ず36未満である
②$n$は必ず36より大きい
③$n$と36との大小はわからない
(5)(4)の図書委員会が行った調査結果による母平均$m$に対する信頼度95%の
信頼区間を$D_1 \leqq m \leqq D_2$、校長先生が行った調査結果による母平均$m$に対す
る信頼度95%の信頼区間を(3)の$C_1 \leqq m \leqq C_2$とする。ただし、母集団は同一
であり、1週間の読書時間の母標準偏差は150とする。
このとき、次の⓪~⑤のうち、正しいものは$\boxed{\boxed{\ \ ソ\ \ }}と\boxed{\boxed{\ \ タ\ \ }}$である。
$\boxed{\boxed{\ \ ソ\ \ }}$, $\boxed{\boxed{\ \ タ\ \ }}$の解答群(解答の順序は問わない。)
⓪$C_1=D_1とC_2=D_2$が必ず成り立つ。
①$C_1 \lt D_2$または$D_1 \lt C_2$のどちらか一方のみが成り立つ。
②$D_2 \lt C_1$または$C_2 \lt D_1$となる場合もある。
③$C_2-C_1 \gt D_2-D_1$が必ず成り立つ。
④$C_2-C_1 = D_2-D_1$が必ず成り立つ。
⑤$C_2-C_1 \lt D_2-D_1$が必ず成り立つ。
2021共通テスト過去問
受験生必見!!円と相似

単元:
#数学(中学生)#中3数学#数A#図形の性質#相似な図形#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円と相似まとめ
*図は動画内参照
この動画を見る
円と相似まとめ
*図は動画内参照
二次関数:東京都立産業技術高等専門学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#東京都立産業技術高等専門学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立産業技術高等専門学校
次の等式が成り立つように
$x^2 - 6x − 7 = (x − \boxed{ ① } )^2 -\boxed{ ② }$
$\boxed{ ① },\boxed{ ② }$
に当てはまる 正の数を求めよ。
この動画を見る
入試問題 東京都立産業技術高等専門学校
次の等式が成り立つように
$x^2 - 6x − 7 = (x − \boxed{ ① } )^2 -\boxed{ ② }$
$\boxed{ ① },\boxed{ ② }$
に当てはまる 正の数を求めよ。
【中学数学】平面図形の演習・証明~岐阜県公立高校入試2018年度~【高校受験】

単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)#受験年度の数字を含む問題
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
動画内図で、$\triangle BDC$と$\triangle ACE$はともに正三角形である。
また、線分ADとBEとの交点をF,ADと辺BCとの交点をGとする。
(1) $\triangle ADC \equiv EBC$であることを証明せよ。
(2) AB=4cm,AC=4cm,BC=6cmのとき、
(ア) DGの長さを求めよ。
(イ) EFの長さを求めよ。
この動画を見る
動画内図で、$\triangle BDC$と$\triangle ACE$はともに正三角形である。
また、線分ADとBEとの交点をF,ADと辺BCとの交点をGとする。
(1) $\triangle ADC \equiv EBC$であることを証明せよ。
(2) AB=4cm,AC=4cm,BC=6cmのとき、
(ア) DGの長さを求めよ。
(イ) EFの長さを求めよ。
#1 数検準1級一次過去問 連立方程式

単元:
#連立方程式#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#ユークリッド互除法と不定方程式・N進法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
3^{x+1}-2・3^y=-9 \\
\log_2 (x+1)-\log_2 (y+2)=-1
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\boxed{1}$これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
3^{x+1}-2・3^y=-9 \\
\log_2 (x+1)-\log_2 (y+2)=-1
\end{array}
\right.
\end{eqnarray}$
入試予想問題:関西学院高等部~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#関西学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試予想問題 関西学院高等部
【難問・奇問は少ない】
次の問題に答えよ。
・$(\sqrt{ 12 }-\sqrt{ 2 })^2+(\sqrt{ 8 }-\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }})(\sqrt{ 48 }+8)$
・$(-\displaystyle \frac{4}{3}x^2y)^3\div(\displaystyle \frac{y}{6x})^2 \times (\displaystyle \frac{y^2}{2x})^3$
次の2つの連立方程式が
同じ解をもつとき、$a、ℓ$私の値を求めなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + 2y = 3 \\
ax +ℓ y = -7
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + 3y = 5 \\
ax +ℓ y = 1
\end{array}
\right.
\end{eqnarray}$
$A,B,C,D,E$の$5$人が図$1$のような
車で出かける計画している。
★$E$は必ず後部座席にすわる。
(1)$5$人の座席配置は全部で何通り?
以下、行きは図2で、帰りは行きと異なる。
(2)$B$が運転席、$A$が助手席に座る。
$5$人の座席配置は全部で向通り?
※図は動画内参照
この動画を見る
入試予想問題 関西学院高等部
【難問・奇問は少ない】
次の問題に答えよ。
・$(\sqrt{ 12 }-\sqrt{ 2 })^2+(\sqrt{ 8 }-\displaystyle \frac{\sqrt{ 3 }}{\sqrt{ 2 }})(\sqrt{ 48 }+8)$
・$(-\displaystyle \frac{4}{3}x^2y)^3\div(\displaystyle \frac{y}{6x})^2 \times (\displaystyle \frac{y^2}{2x})^3$
次の2つの連立方程式が
同じ解をもつとき、$a、ℓ$私の値を求めなさい。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + 2y = 3 \\
ax +ℓ y = -7
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + 3y = 5 \\
ax +ℓ y = 1
\end{array}
\right.
\end{eqnarray}$
$A,B,C,D,E$の$5$人が図$1$のような
車で出かける計画している。
★$E$は必ず後部座席にすわる。
(1)$5$人の座席配置は全部で何通り?
以下、行きは図2で、帰りは行きと異なる。
(2)$B$が運転席、$A$が助手席に座る。
$5$人の座席配置は全部で向通り?
※図は動画内参照
【高校受験対策/数学】死守67

単元:
#数学(中学生)#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#比例・反比例#平行と合同#確率#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守67
① 2次方程式を$x^3+3x-1=0$を解きなさい。
②$\sqrt{24}\div\sqrt{3}-\sqrt{2}$を計算しなさい。
③関数$y=\frac{3}{x}$について、$x$の変域が$1 \leqq x \leqq 6$のとき、$y$の変域を答えなさい。
④
$x$枚の空の封筒と$y$本の鉛筆がある。
封筒の中に鉛筆を4本ずつ入れると8本足りず、3本ずつ入れると12本余る。
このとき$x$と$y$の値を求めなさい。
⑤
右の図のような、$AD=2cm$、$BC=5cm$、$AD/\!/BC$である台形$ABCD$があり、対角線$AC$、$BD$の交点を$E$とする。
点$E$から辺$DC$上に辺$BC$と線分$EF$が平行となる点$F$をとるとき、線分$EF$の長さを答えなさい。
⑥
1から6までの目のついた大、小2つのさいころを同時に投げたとき、大きいさいころの出た目の数を$a$、小さいさいころの出た目の数を$b$とする。
このとき、出た目の数の積$a×b$の値が25以下となる確率を求めなさい。
⑦
右の図のように直線$l$と2つの点$A$、$B$がある。
直線$l$上にあって、2つの点$A$、$B$を通る円の中心$P$を、定規とコンパスを用いて作図しなさい。
ただし作図に使った線は消さずに残しておくこと。
この動画を見る
高校受験対策・死守67
① 2次方程式を$x^3+3x-1=0$を解きなさい。
②$\sqrt{24}\div\sqrt{3}-\sqrt{2}$を計算しなさい。
③関数$y=\frac{3}{x}$について、$x$の変域が$1 \leqq x \leqq 6$のとき、$y$の変域を答えなさい。
④
$x$枚の空の封筒と$y$本の鉛筆がある。
封筒の中に鉛筆を4本ずつ入れると8本足りず、3本ずつ入れると12本余る。
このとき$x$と$y$の値を求めなさい。
⑤
右の図のような、$AD=2cm$、$BC=5cm$、$AD/\!/BC$である台形$ABCD$があり、対角線$AC$、$BD$の交点を$E$とする。
点$E$から辺$DC$上に辺$BC$と線分$EF$が平行となる点$F$をとるとき、線分$EF$の長さを答えなさい。
⑥
1から6までの目のついた大、小2つのさいころを同時に投げたとき、大きいさいころの出た目の数を$a$、小さいさいころの出た目の数を$b$とする。
このとき、出た目の数の積$a×b$の値が25以下となる確率を求めなさい。
⑦
右の図のように直線$l$と2つの点$A$、$B$がある。
直線$l$上にあって、2つの点$A$、$B$を通る円の中心$P$を、定規とコンパスを用いて作図しなさい。
ただし作図に使った線は消さずに残しておくこと。
市川 整数 D

単元:
#計算と数の性質#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)129と282の最小公倍数は?
(2)自然数A,Bの最大公約数をG、最小公倍数をLとする。
A,BをGで割ったときの商をそれぞれa,bとする。
(ⅰ)Lをa,b,Gで表せ
(ⅱ)A-2B-2G+L=2021のとき(A,B)をすべて求めよ。(G≠1)
2021市川高等学校
この動画を見る
(1)129と282の最小公倍数は?
(2)自然数A,Bの最大公約数をG、最小公倍数をLとする。
A,BをGで割ったときの商をそれぞれa,bとする。
(ⅰ)Lをa,b,Gで表せ
(ⅱ)A-2B-2G+L=2021のとき(A,B)をすべて求めよ。(G≠1)
2021市川高等学校
2021 日大習志野 角の和
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
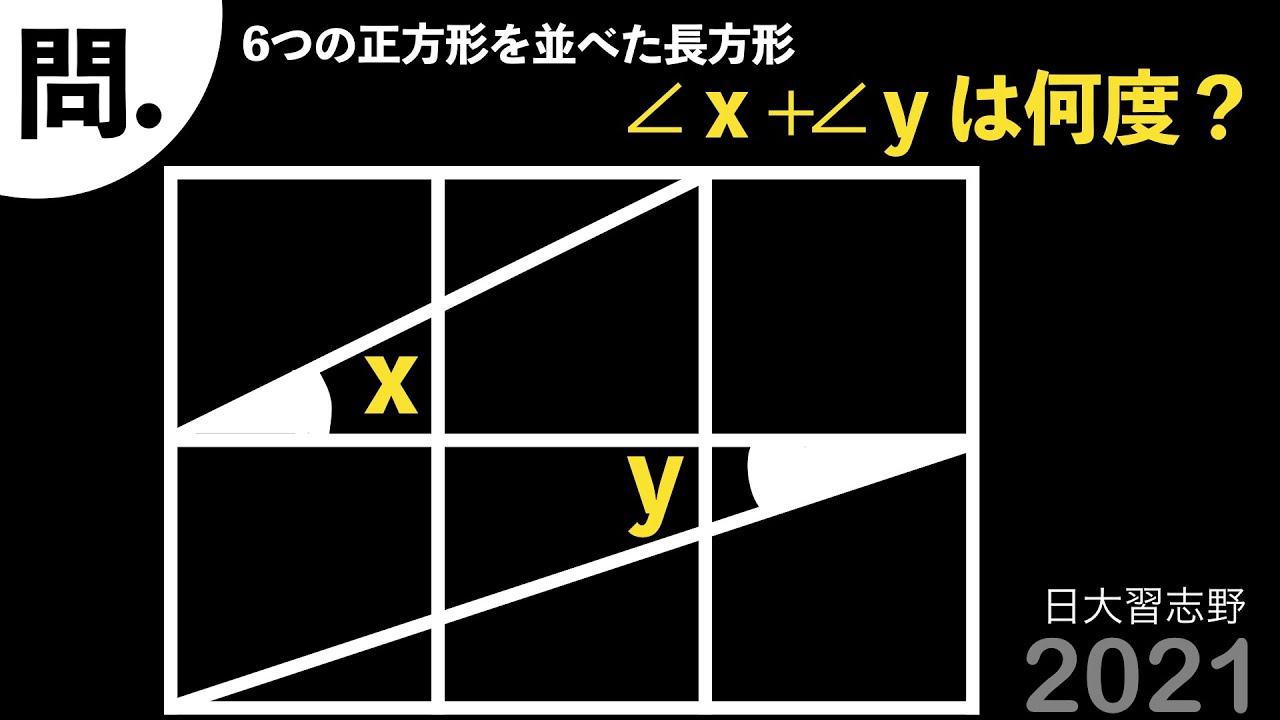
6つの正方形を並べた長方形
$\angle x + \angle y = ?$
2021日本大学習志野高等学校
この動画を見る
6つの正方形を並べた長方形
$\angle x + \angle y = ?$
2021日本大学習志野高等学校
円錐台 内接球 2021 C

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
球を除いた体積=?
*図は動画内参照
2021専修大学松戸高等学校
この動画を見る
球を除いた体積=?
*図は動画内参照
2021専修大学松戸高等学校
2021 平方根と因数分解 A 昭和学院秀英
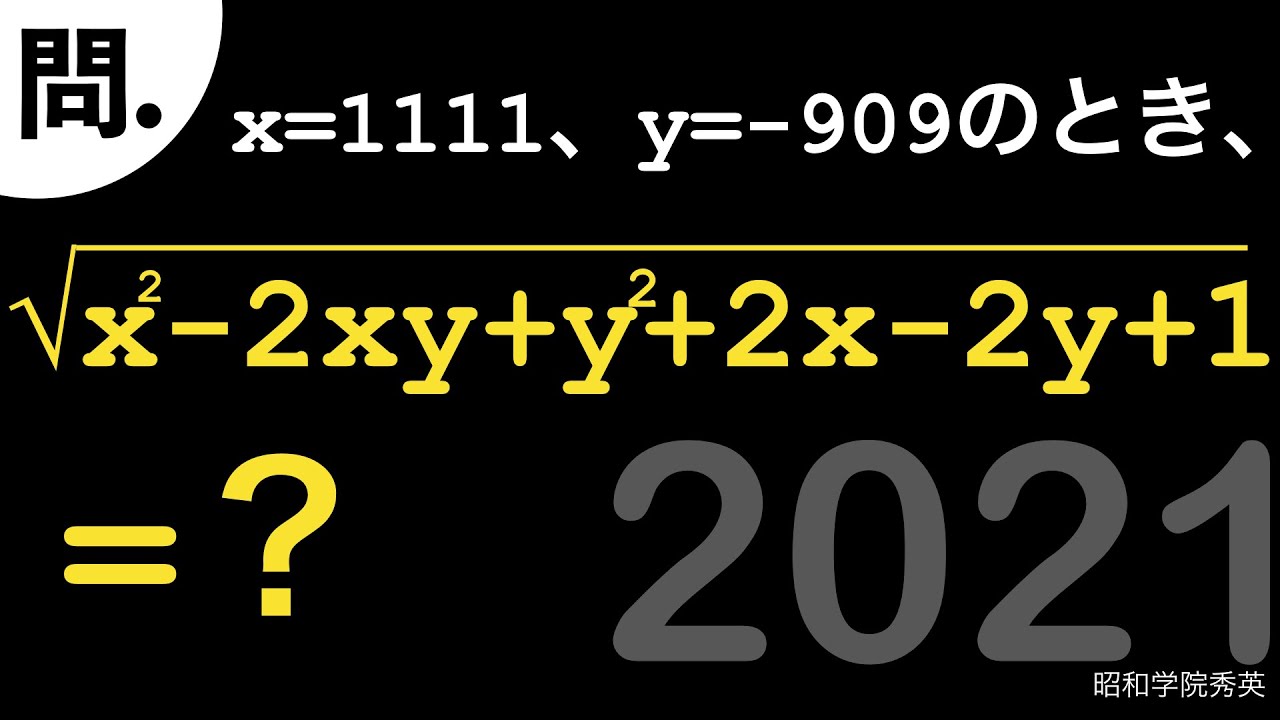
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
x=1111,y=-909のとき
$\sqrt{x^2-2xy+y^2+2x-2y+1} =?$
2021昭和学院秀英高等学校
この動画を見る
x=1111,y=-909のとき
$\sqrt{x^2-2xy+y^2+2x-2y+1} =?$
2021昭和学院秀英高等学校
平方根:洛南高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 洛南高等学校
$(1+\sqrt{ 2 }-\sqrt{ 3 })(\sqrt{ 2 }+\sqrt{ 4 }+\sqrt{ 6 })$
計算をせよ。
この動画を見る
入試問題 洛南高等学校
$(1+\sqrt{ 2 }-\sqrt{ 3 })(\sqrt{ 2 }+\sqrt{ 4 }+\sqrt{ 6 })$
計算をせよ。
2021渋谷幕張 円 D
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
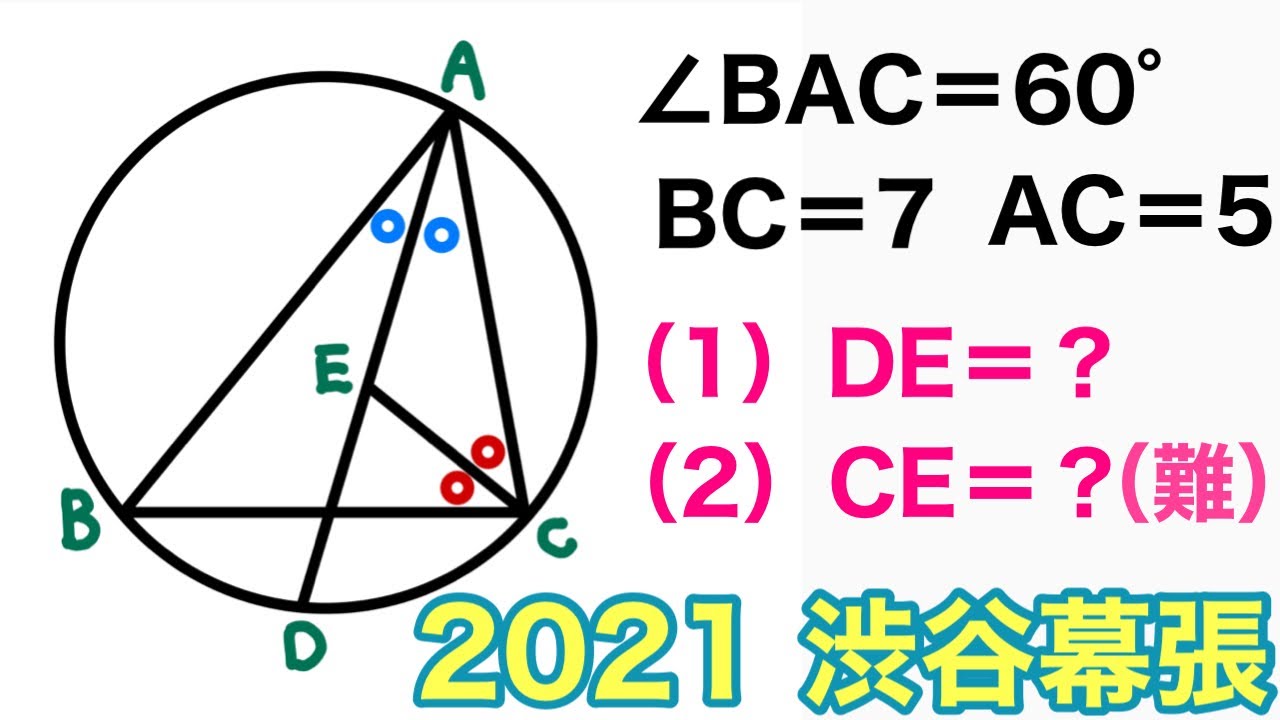
$\angle BAC=60°$
(1)DE=?
(2)CE=?
*図は動画内参照
2021渋谷教育学園幕張高等学校
この動画を見る
$\angle BAC=60°$
(1)DE=?
(2)CE=?
*図は動画内参照
2021渋谷教育学園幕張高等学校
2021昭和学院秀英 確率

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2⃣、3⃣、4⃣、5⃣、6⃣
5枚のカードから無作為に1枚取り出し数字を記録して戻す作業を3回繰り返したとき、記録した数字の積が4の倍数となる確率を求めよ。
2021昭和学院秀英高等学校
この動画を見る
2⃣、3⃣、4⃣、5⃣、6⃣
5枚のカードから無作為に1枚取り出し数字を記録して戻す作業を3回繰り返したとき、記録した数字の積が4の倍数となる確率を求めよ。
2021昭和学院秀英高等学校
2021昭和秀英 正四角錐の外接球
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
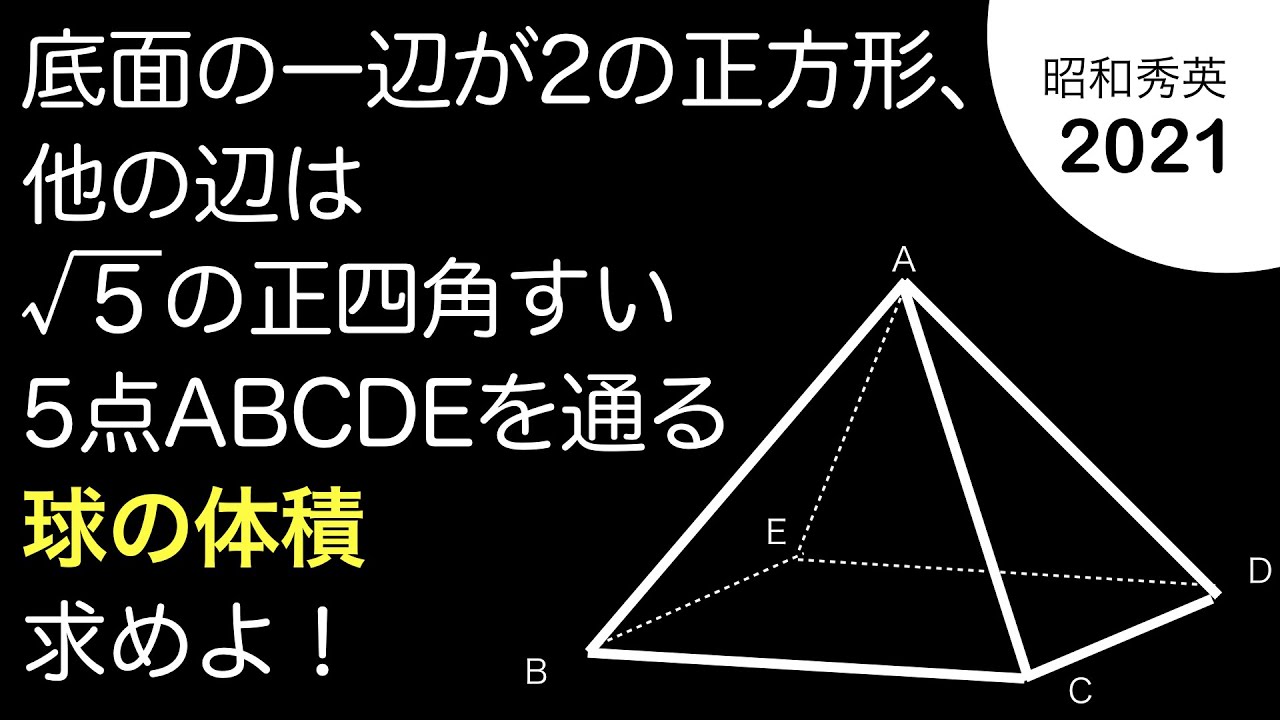
底面の一辺が2の正方形、他の辺は$\sqrt 5$の正四角すい
5点ABCDEを通る球の体積を求めよ。
*図は動画内参照
2021昭和学院秀英高等学校
この動画を見る
底面の一辺が2の正方形、他の辺は$\sqrt 5$の正四角すい
5点ABCDEを通る球の体積を求めよ。
*図は動画内参照
2021昭和学院秀英高等学校
瞬殺!!三角形の面積二等分 慶應義塾
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
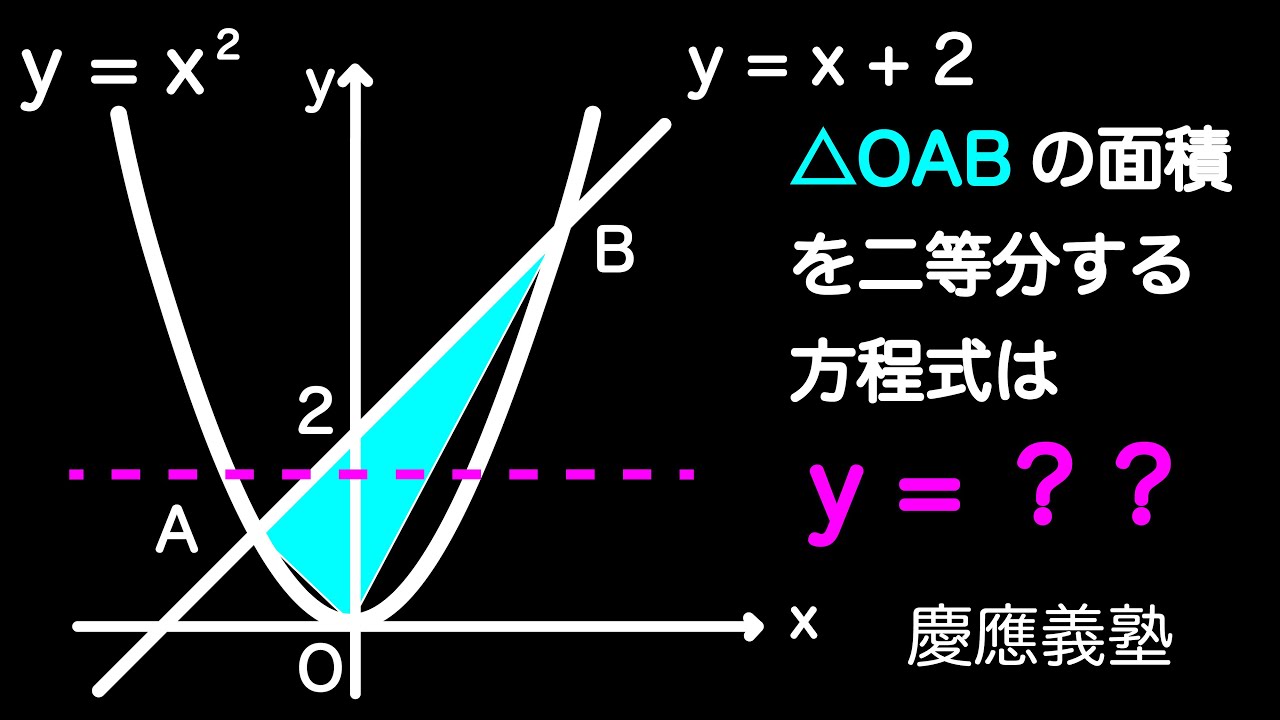
△OABの面積を二等分するx軸に平行な直線の式を求めよ。
*図は動画内参照
慶應義塾高等学校
この動画を見る
△OABの面積を二等分するx軸に平行な直線の式を求めよ。
*図は動画内参照
慶應義塾高等学校
確率:洛南高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#洛南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
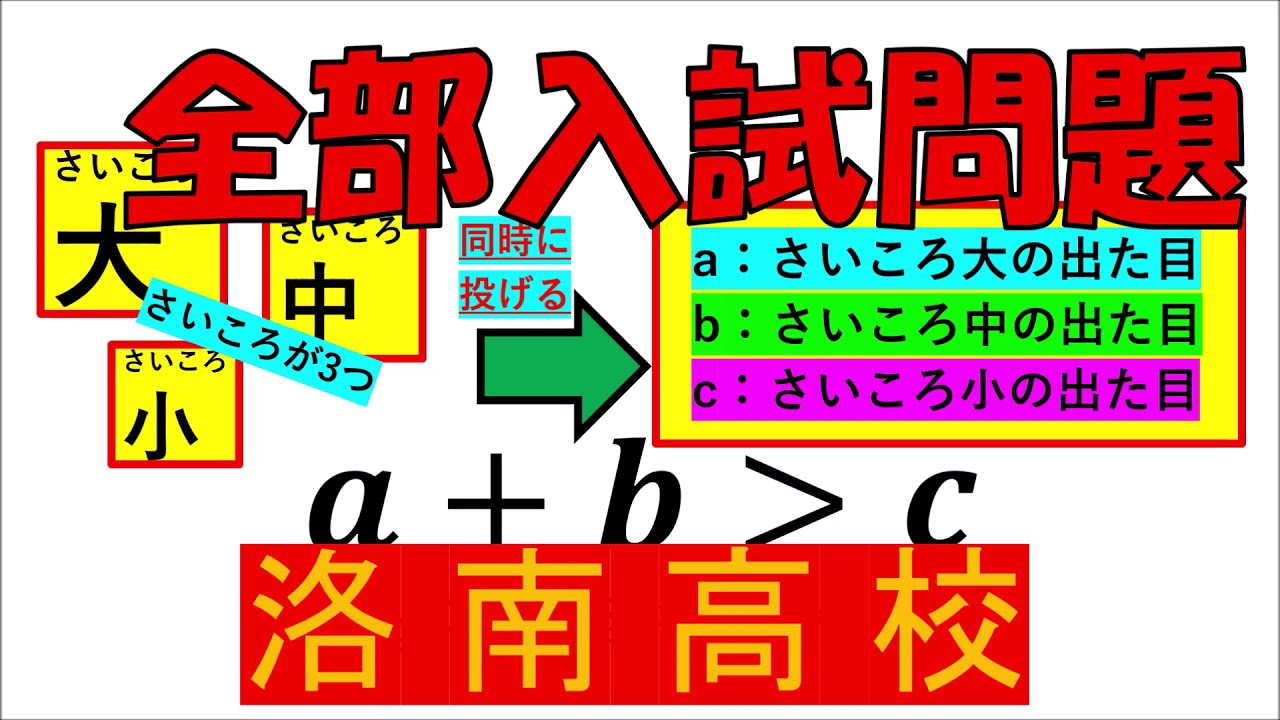
入試問題 洛南高等学校
サイズが異なるさいころを同時に投げ、
a: さいころ大の出た目
b: さいころ中の出た目
c: さいころ小の出た目
$a+b \gt c$
となる確率を求めよ。
この動画を見る
入試問題 洛南高等学校
サイズが異なるさいころを同時に投げ、
a: さいころ大の出た目
b: さいころ中の出た目
c: さいころ小の出た目
$a+b \gt c$
となる確率を求めよ。
中2も解ける平面図形 C
単元:
#数学(中学生)#平面図形#角度と面積#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
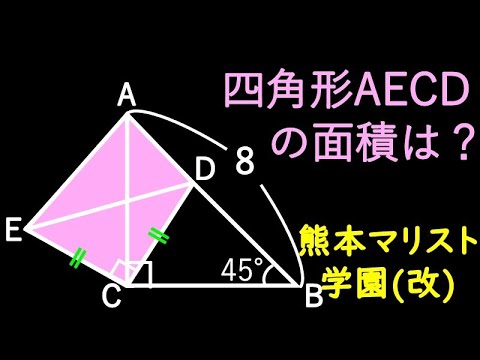
四角形AECDの面積=?
*図は動画内参照
熊本マリスト学園高等学校(改)
この動画を見る
四角形AECDの面積=?
*図は動画内参照
熊本マリスト学園高等学校(改)
整数:西大和学園高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#西大和学園高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 西大和学園高等学校
$x,y$は整数。$x \gt y$を満たす。
$x^2 = 25 + y^2 $ を満たす
整数の組$(x, y)$を全て求めよ。
この動画を見る
入試問題 西大和学園高等学校
$x,y$は整数。$x \gt y$を満たす。
$x^2 = 25 + y^2 $ を満たす
整数の組$(x, y)$を全て求めよ。
一定であることの証明 慶應志木
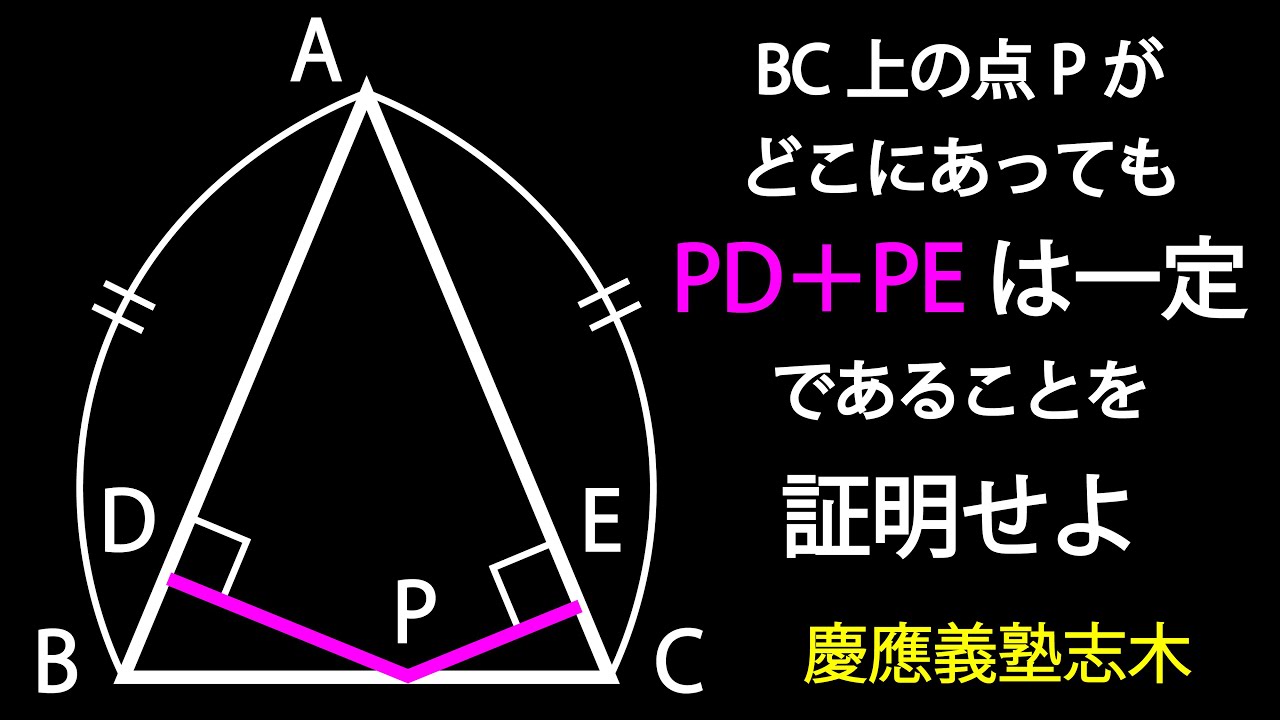
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
PD+PE=一定であることを証明せよ。
*図は動画内参照
慶應義塾志木高等学校
この動画を見る
PD+PE=一定であることを証明せよ。
*図は動画内参照
慶應義塾志木高等学校
【中学数学】式の計算:等式変形マスターへの道 8発目!『最初に全部割れる編』 6x +4=8yをx=の形にしましょう。(すみません!まだあった!)

二次方程式:明治大学付属明治高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 明治大学付属明治高等学校
$x$についての$2$次方程式
$x^2 - (a^2 - 4a + 5) x + 5a(a – 4) = 0$
($a$が正の整数)
解が1つ になる。→ $a$の値を求めよ。
この動画を見る
入試問題 明治大学付属明治高等学校
$x$についての$2$次方程式
$x^2 - (a^2 - 4a + 5) x + 5a(a – 4) = 0$
($a$が正の整数)
解が1つ になる。→ $a$の値を求めよ。
円 三角形の合同の証明 B
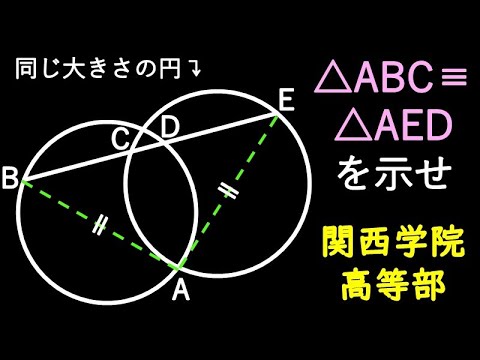
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
同じ大きさの円
△ABC≡△AEDを示せ
*図は動画内参照
関西学院高等部
この動画を見る
同じ大きさの円
△ABC≡△AEDを示せ
*図は動画内参照
関西学院高等部
文章題:西大和学園高等学校全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#西大和学園高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 西大和学園高等学校
ある試験において
合格基準点に対して
合格者の平均点:+4点
不合格者の平均点:-8点
全受験者の 平均点:60点
合格基準点は何点か求めよ。
この動画を見る
入試問題 西大和学園高等学校
ある試験において
合格基準点に対して
合格者の平均点:+4点
不合格者の平均点:-8点
全受験者の 平均点:60点
合格基準点は何点か求めよ。
文字式:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 慶応義塾高等学校
次の空欄をうめよ。
$3x^2 - 15x +7=0$ のとき
→$3x^4 – 15x^3 + 35x – 16 $
の値は▭である。
この動画を見る
入試問題 慶応義塾高等学校
次の空欄をうめよ。
$3x^2 - 15x +7=0$ のとき
→$3x^4 – 15x^3 + 35x – 16 $
の値は▭である。
