 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
【一度解いてみたくなる…!】文字式:函館白百合学園高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#函館白百合学園高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x=\dfrac{3}{4},y=\dfrac{7}{4}$のとき,
$(3x-2y)^2-(3x+2y)^2$の値を求めなさい.
函館白百合学園高等学校過去問
この動画を見る
$ x=\dfrac{3}{4},y=\dfrac{7}{4}$のとき,
$(3x-2y)^2-(3x+2y)^2$の値を求めなさい.
函館白百合学園高等学校過去問
因数分解を解くコツをつかもう!~全国入試問題解法 #shorts, #数学, #高校受験, #頭の体操
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
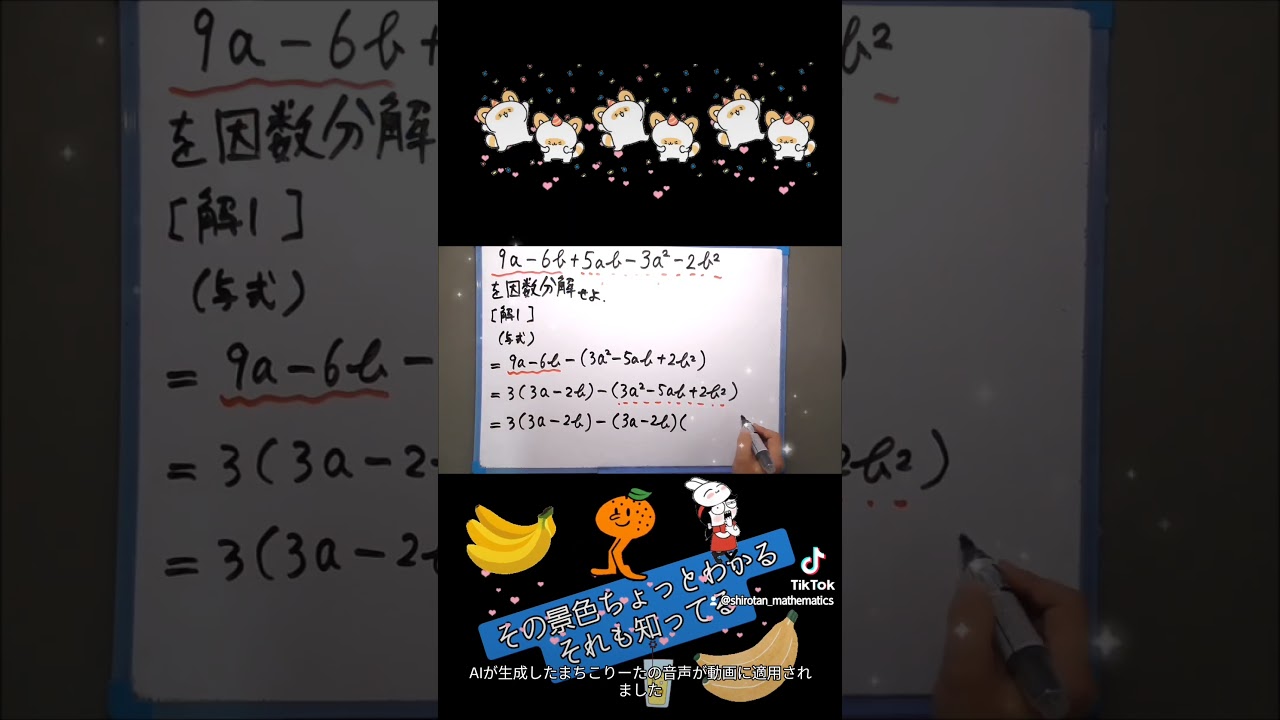
$ 9a-6b+5ab-3a^2-2b^2 $を因数分解せよ.
西大和学園高校過去問
この動画を見る
$ 9a-6b+5ab-3a^2-2b^2 $を因数分解せよ.
西大和学園高校過去問
中1の4月に出来て欲しい計算
単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
①$(+2)+(+5)$
②$(+4)+(-2)$
③$(-7)+(+20)$
④$(+2)-(+1)$
⑤$(+9)-(+10)$
⑥$(-5)-(+5)$
⑦$(+1)-(-3)$
この動画を見る
①$(+2)+(+5)$
②$(+4)+(-2)$
③$(-7)+(+20)$
④$(+2)-(+1)$
⑤$(+9)-(+10)$
⑥$(-5)-(+5)$
⑦$(+1)-(-3)$
【問題のホンシツをつかめ…!】整数:大阪教育大学附属高等学校池田校舎~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#大阪教育大学附属高等学校池田校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt n $を電卓を使って少数で表し,小数第一位で四捨五入すると8になった.
このような自然数nはいくつあるか.
大阪教育大学附属高等学校池田校舎過去問
この動画を見る
$ \sqrt n $を電卓を使って少数で表し,小数第一位で四捨五入すると8になった.
このような自然数nはいくつあるか.
大阪教育大学附属高等学校池田校舎過去問
【サンペンの長さと言えば…!】三平方の定理:興南高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#興南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
3辺の長さがそれぞれ$ x+3,x+2,x-5 $である三角形が直角三角形であるとき・・・
xの値を求めなさい.
興南高等学校過去問
この動画を見る
3辺の長さがそれぞれ$ x+3,x+2,x-5 $である三角形が直角三角形であるとき・・・
xの値を求めなさい.
興南高等学校過去問
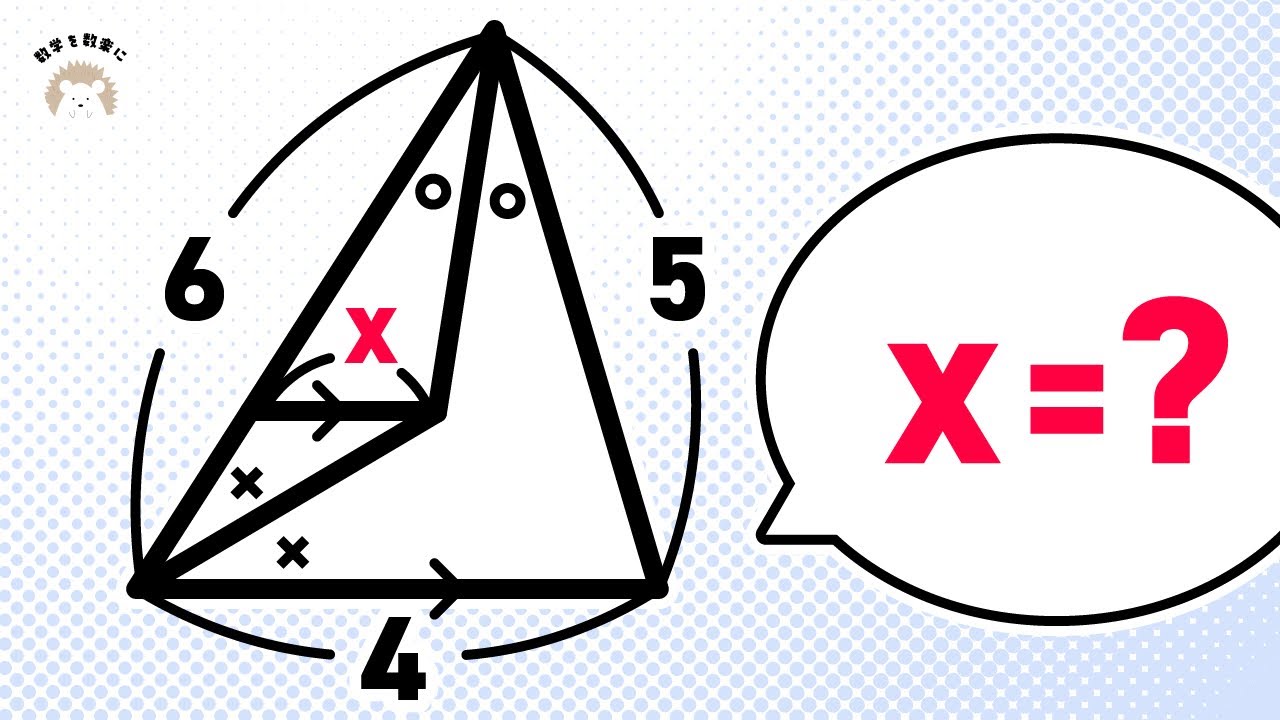
三角形の内角の二等分線と言われたら?
【ポイントは2つ…!】立体図形:精華女子高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#精華女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
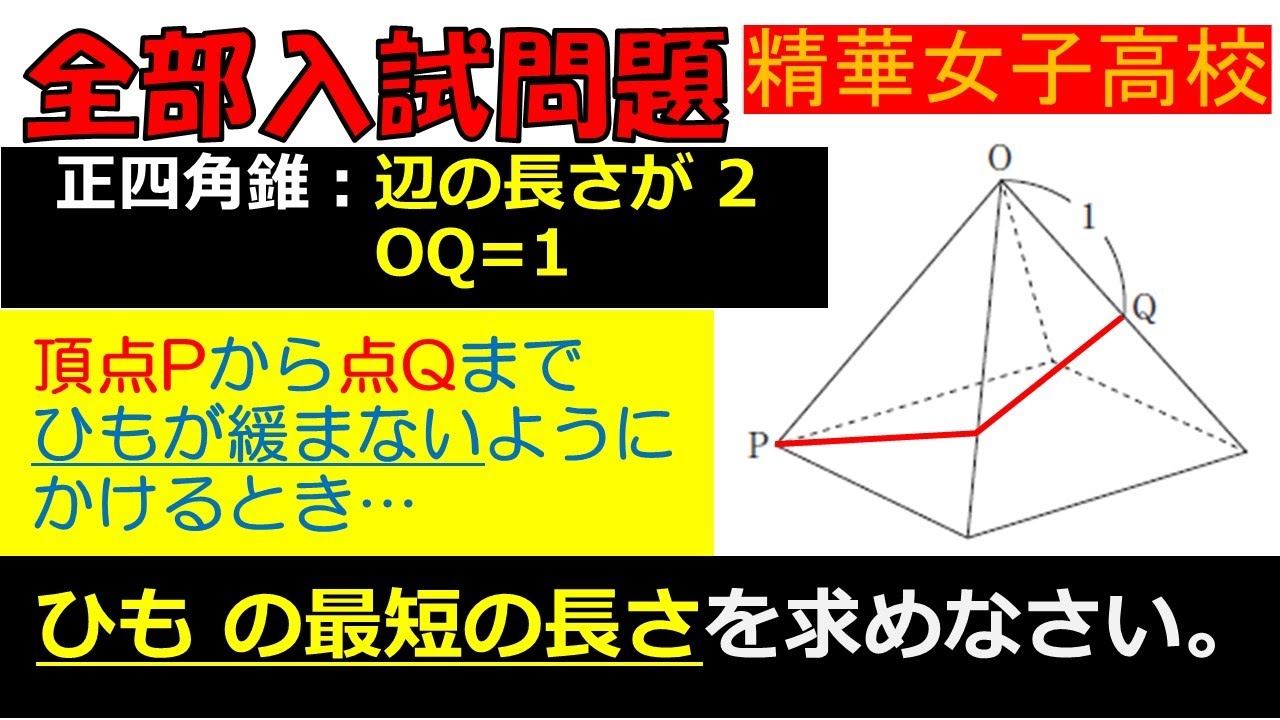
正四角錐のすべての辺の長さが2cmであり,OQ=1cmである.
頂点Pから点Qまでひもが緩まないようにかけるとき・・・
ひもの最短の長さを求めなさい.
精華女子高等学校過去問
この動画を見る
正四角錐のすべての辺の長さが2cmであり,OQ=1cmである.
頂点Pから点Qまでひもが緩まないようにかけるとき・・・
ひもの最短の長さを求めなさい.
精華女子高等学校過去問
【知ってる or 知らない…!】平方根:興南高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#興南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の計算をしなさい.
$ \left(\dfrac{\sqrt{432}}{\sqrt3} \right)^2+\sqrt{121}\div \left(-\dfrac{1}{\sqrt9}\right)$
興南高等学校過去問
この動画を見る
次の計算をしなさい.
$ \left(\dfrac{\sqrt{432}}{\sqrt3} \right)^2+\sqrt{121}\div \left(-\dfrac{1}{\sqrt9}\right)$
興南高等学校過去問
【数学】中高一貫校問題集2幾何158:三平方の定理:線分の長さ

単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
BC=CA=8cm, 面積が4√15cm²の△ABCにおいて、辺BCの中点をMとし、点Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分HMの長さを求めなさい。
(2)線分ABの長さを求めなさい。
この動画を見る
BC=CA=8cm, 面積が4√15cm²の△ABCにおいて、辺BCの中点をMとし、点Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分HMの長さを求めなさい。
(2)線分ABの長さを求めなさい。
文字式:分数に平方根が現れたら…!~全国入試問題解法 #shorts, #数学, #高校入試, #頭の体操, #サウンド

単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x=\sqrt7+\sqrt5$
$ y=\sqrt7-\sqrt5 $ のとき$ \dfrac{(\sqrt x-\sqrt y)}{(\sqrt x+\sqrt y)}$の値を求めなさい.
全国入試過去問
この動画を見る
$ x=\sqrt7+\sqrt5$
$ y=\sqrt7-\sqrt5 $ のとき$ \dfrac{(\sqrt x-\sqrt y)}{(\sqrt x+\sqrt y)}$の値を求めなさい.
全国入試過去問
【数学】中高一貫校問題集2幾何157:三平方の定理:三角形の面積

単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
AB=14cm, BC=15cm, CA=13cmである△ABCにおいて、Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分BHの長さを求めなさい。
(2)△ABCの面積を求めなさい。
この動画を見る
AB=14cm, BC=15cm, CA=13cmである△ABCにおいて、Aから辺BCに引いた垂線と辺BCとの交点をHとする。
(1)線分BHの長さを求めなさい。
(2)△ABCの面積を求めなさい。
【数学】中高一貫校問題集2幾何156:直角三角形の3辺の長さの決定

単元:
#数学(中学生)#中3数学#円
教材:
#TK数学#TK数学問題集2(幾何編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
3辺の長さが(x-5)cm,(x+2)cm,(x+3)cmで表される直角三角形がある。このとき、xの値を求めなさい。
この動画を見る
3辺の長さが(x-5)cm,(x+2)cm,(x+3)cmで表される直角三角形がある。このとき、xの値を求めなさい。
【分かる人が次に進む…!】二次関数:日本大学第三高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#日本大学第三高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
関数$ y=\dfrac{1}{2}x^2 $について
xの変域が$ a-3 \leqq x \leqq a+3$のとき,yの変域は$ b \leqq y \leqq 8$である.
*但し, $ -3 \lt a \lt 0 $
定数$ a,b $の値を求めなさい.
この動画を見る
関数$ y=\dfrac{1}{2}x^2 $について
xの変域が$ a-3 \leqq x \leqq a+3$のとき,yの変域は$ b \leqq y \leqq 8$である.
*但し, $ -3 \lt a \lt 0 $
定数$ a,b $の値を求めなさい.
なんでこんなに速い?

【完答できるか…!?】文章題:興南高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#興南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2つの負の数がある.
この2つの数の差が7で積が144であるとき,小さい方の数を求めなさい.
興南高等学校過去問
この動画を見る
2つの負の数がある.
この2つの数の差が7で積が144であるとき,小さい方の数を求めなさい.
興南高等学校過去問
#63 #数検1級1次過去問 #連立方程式

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
ますただ
問題文全文(内容文):
$xy \neq 0$のとき、次の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)(x^2+y^2)=\displaystyle \frac{40}{3}xy \\
(x^2+y^2)(x^4-y^4)=\displaystyle \frac{800}{9}x^2y^2
\end{array}
\right.
\end{eqnarray}$
出典:数検1級1次
この動画を見る
$xy \neq 0$のとき、次の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)(x^2+y^2)=\displaystyle \frac{40}{3}xy \\
(x^2+y^2)(x^4-y^4)=\displaystyle \frac{800}{9}x^2y^2
\end{array}
\right.
\end{eqnarray}$
出典:数検1級1次
偶数

難関私立高校でよく使う考え方 ルートの計算
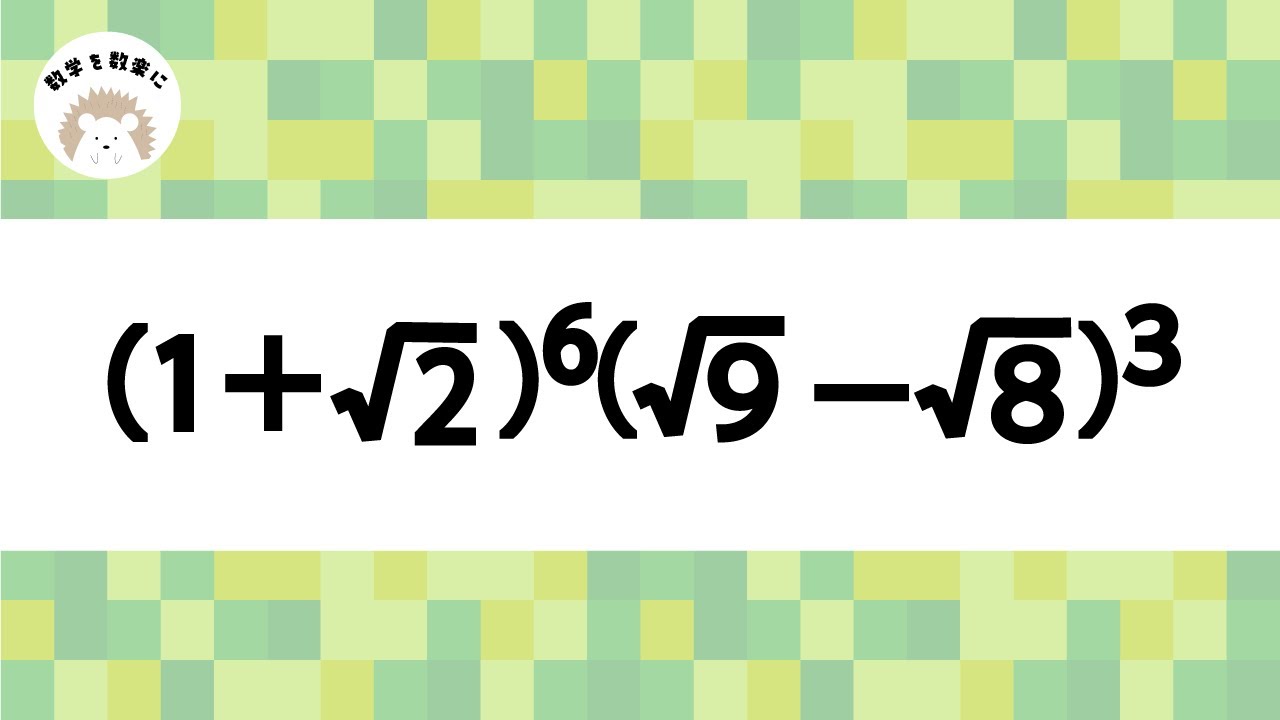
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
$(1+\sqrt 2)^6(\sqrt 9 - \sqrt 8 )^3$
この動画を見る
$(1+\sqrt 2)^6(\sqrt 9 - \sqrt 8 )^3$
【使えるものは使え…!】整数:同志社高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#同志社高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
Nは十の位の数字がa,一の位の数字がbである2桁の自然数である.
MはNの十の位の数字と一の位の数字を入れ替えてできる自然数である.
$ N^2-M^2=693 $であるとき,自然数Nを求めよ.
同志社高等学校過去問
この動画を見る
Nは十の位の数字がa,一の位の数字がbである2桁の自然数である.
MはNの十の位の数字と一の位の数字を入れ替えてできる自然数である.
$ N^2-M^2=693 $であるとき,自然数Nを求めよ.
同志社高等学校過去問
文字式を解くにはパターンがある~全国入試問題解法 #shorts, #数学, #高校入試, #頭の体操
単元:
#数学(中学生)#中1数学#文字と式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
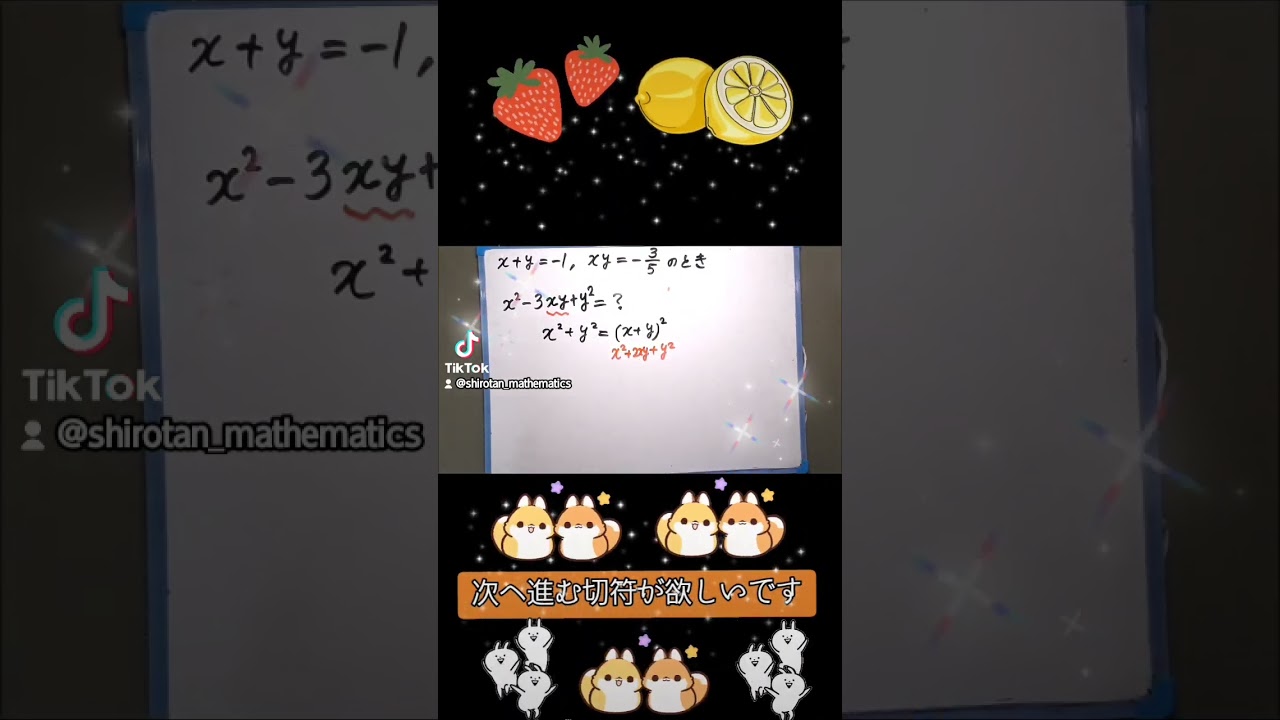
$ x+y=-1,xy=-\dfrac{3}{5}$のとき,
$ x^2-3xy+y^2$の値を求めなさい.
法政大第二高校過去問
この動画を見る
$ x+y=-1,xy=-\dfrac{3}{5}$のとき,
$ x^2-3xy+y^2$の値を求めなさい.
法政大第二高校過去問
数学を数楽に

2通りで解説 円の面積

【ライバルは多い…!】因数分解:中央大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ a^2b^2-2abd-c^2+d^2 $を因数分解しなさい.
中央大附属高校過去問
この動画を見る
$ a^2b^2-2abd-c^2+d^2 $を因数分解しなさい.
中央大附属高校過去問
式の値
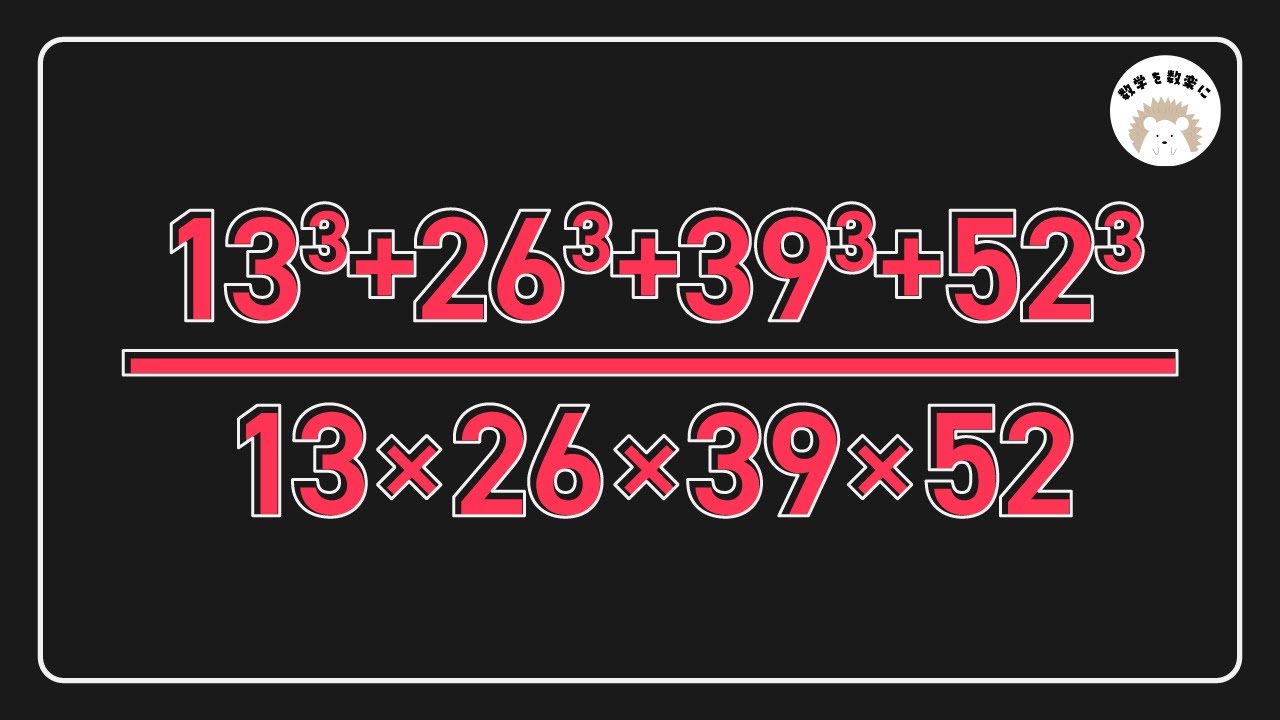
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{13^3+26^3+39^3+52^3}{13×26×39×52}$
この動画を見る
$\frac{13^3+26^3+39^3+52^3}{13×26×39×52}$
#62 #数検1級1次過去問 #因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の式を係数が整数の範囲で因数分解せよ。
$x^6-14x^4+17x^2-4$
出典:数検1級1次
この動画を見る
次の式を係数が整数の範囲で因数分解せよ。
$x^6-14x^4+17x^2-4$
出典:数検1級1次
【初手をどう攻める…!?】整数:大阪教育大学附属高等学校池田校舎~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#大阪教育大学附属高等学校池田校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
1~20までの自然数のうち,
Aは素数であるものの積であり,Bは素数でないものの積である.
AとBの最大公約数を求めなさい.
大教大高校過去問
この動画を見る
1~20までの自然数のうち,
Aは素数であるものの積であり,Bは素数でないものの積である.
AとBの最大公約数を求めなさい.
大教大高校過去問
ルートと二乗
クラス替えで好きな人と同じになる確率

【ロンリ的思考と計算力…!】整数:早稲田大学系属早稲田実業学校高等部~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
a,bは連続しない正の整数とする.
$ (a-b)(a^2+b^2)=2023 $を満たすa,bの値を求めよ.
早稲田大学系属早稲田実業学校高等部過去問
この動画を見る
a,bは連続しない正の整数とする.
$ (a-b)(a^2+b^2)=2023 $を満たすa,bの値を求めよ.
早稲田大学系属早稲田実業学校高等部過去問
高校入試でも何でも計算は工夫をしたい動画~全国入試問題解法 #数学, #高校入試, #偏差値アップ

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の計算をし,$ \Box $に当てはまる数を答えなさい.
$ 340^2-337^2-3^2=\Box $
大教大付属高校過去問
この動画を見る
次の計算をし,$ \Box $に当てはまる数を答えなさい.
$ 340^2-337^2-3^2=\Box $
大教大付属高校過去問
