 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
2023高校入試解説15問目 3種類の4ケタの数 渋谷教育学園幕張 コメントに別解多数あり!!

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
1000~9999の4ケタの整数について2023のようにちょうど3種類の数字が用いられている整数は何個?
2023渋谷教育学園幕張高等学校
この動画を見る
1000~9999の4ケタの整数について2023のようにちょうど3種類の数字が用いられている整数は何個?
2023渋谷教育学園幕張高等学校
2023高校入試解説16問目 3つの内接円 渋谷教育学園幕張

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle QPR=?$
*図は動画内参照
2023渋谷教育学園幕張高等学校
この動画を見る
$\angle QPR=?$
*図は動画内参照
2023渋谷教育学園幕張高等学校
2023高校入試解説14問目 2次方程式 渋谷教育学園幕張

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
方程式を解け
$(x+\sqrt 3 +\sqrt 5)^2 - 3 \sqrt 5(x-2 \sqrt 5 + \sqrt 3 ) -35 = 0$
2023渋谷教育学園幕張高等学校
この動画を見る
方程式を解け
$(x+\sqrt 3 +\sqrt 5)^2 - 3 \sqrt 5(x-2 \sqrt 5 + \sqrt 3 ) -35 = 0$
2023渋谷教育学園幕張高等学校
【中学数学】99%が間違えた円と接線の問題~2022年埼玉県公立高校入試~【高校受験】
単元:
#数学(中学生)#中1数学#平面図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
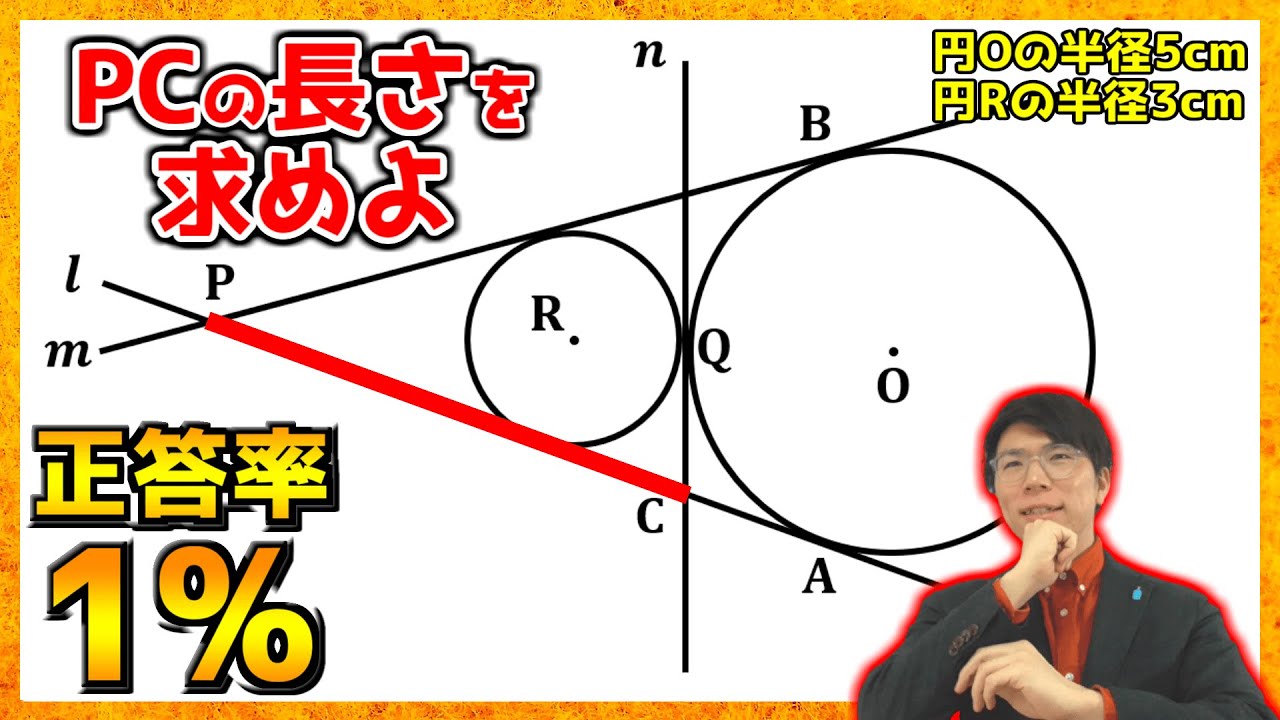
図のように、点Oを中心とする円周上に2点A,Bをとり、A,Bを通る円Oの接線をそれぞれl,mとします。直線lとmとが点Pで交わる。
直線l,mに接し、円Oに点Qで接する円の中心をRとします。また、点Qを通る円Oと円Rの共通の接線をnとし、lとnとの交点をCとします。
円Oの半径が5cm、円Rの半径が3cmであるとき、線分PCの長さを求めよ。
※図は動画内参照
この動画を見る
図のように、点Oを中心とする円周上に2点A,Bをとり、A,Bを通る円Oの接線をそれぞれl,mとします。直線lとmとが点Pで交わる。
直線l,mに接し、円Oに点Qで接する円の中心をRとします。また、点Qを通る円Oと円Rの共通の接線をnとし、lとnとの交点をCとします。
円Oの半径が5cm、円Rの半径が3cmであるとき、線分PCの長さを求めよ。
※図は動画内参照
2023高校入試解説13問目 因数分解昭和学院秀英

単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$a^2 - 4b^2 +3ab -2bc +2ca$
2023昭和学院秀英高等学校
この動画を見る
因数分解せよ
$a^2 - 4b^2 +3ab -2bc +2ca$
2023昭和学院秀英高等学校
2023高校入試解説12問目 台形と半円 解き方2通り 日大習志野(改)

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$AD=\frac{9}{4}$
半円Oの面積=?
*図は動画内参照
2023日本大学習志野高等学校
この動画を見る
$AD=\frac{9}{4}$
半円Oの面積=?
*図は動画内参照
2023日本大学習志野高等学校
【「分かった」ことを「説明」するには…!】図形:富山県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#空間図形#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
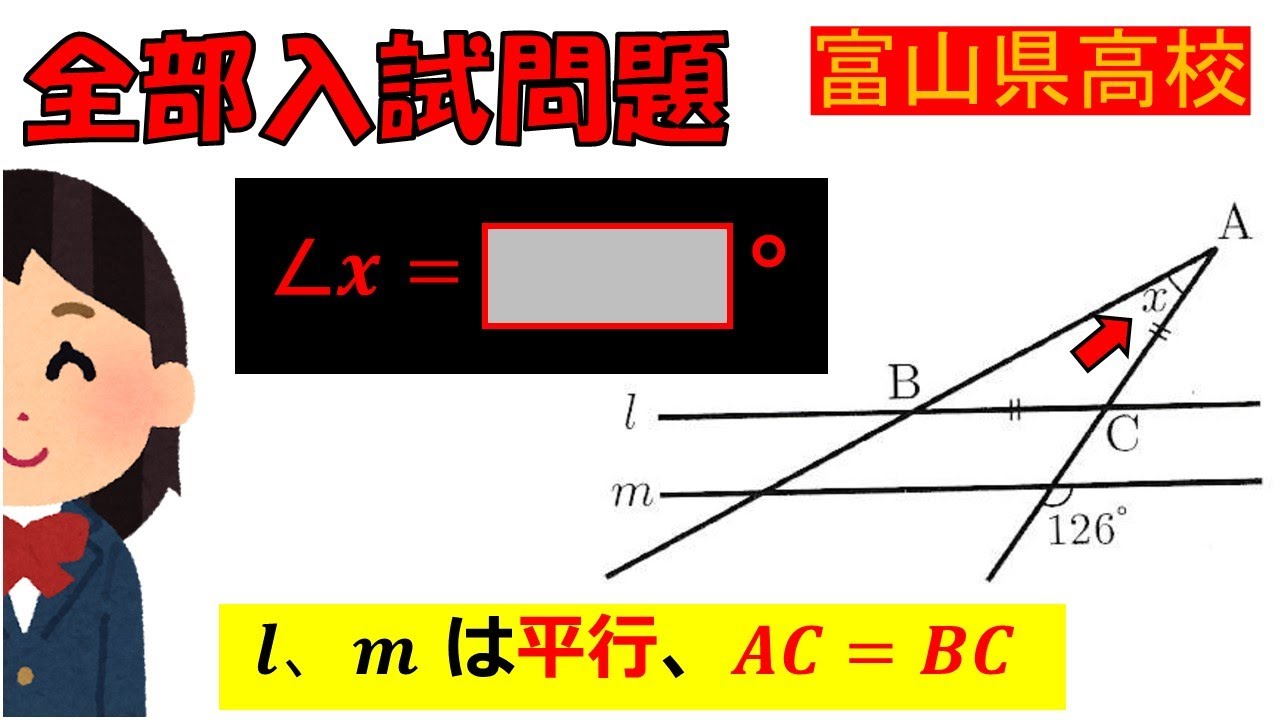
$ l,m$は平行であり,$AC=BC$である.
$ \angle x$は何度であるか.
富山県公立高等学校過去問
この動画を見る
$ l,m$は平行であり,$AC=BC$である.
$ \angle x$は何度であるか.
富山県公立高等学校過去問
2023高校入試解説11問目 円の方程式??2日大習志野(改)
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
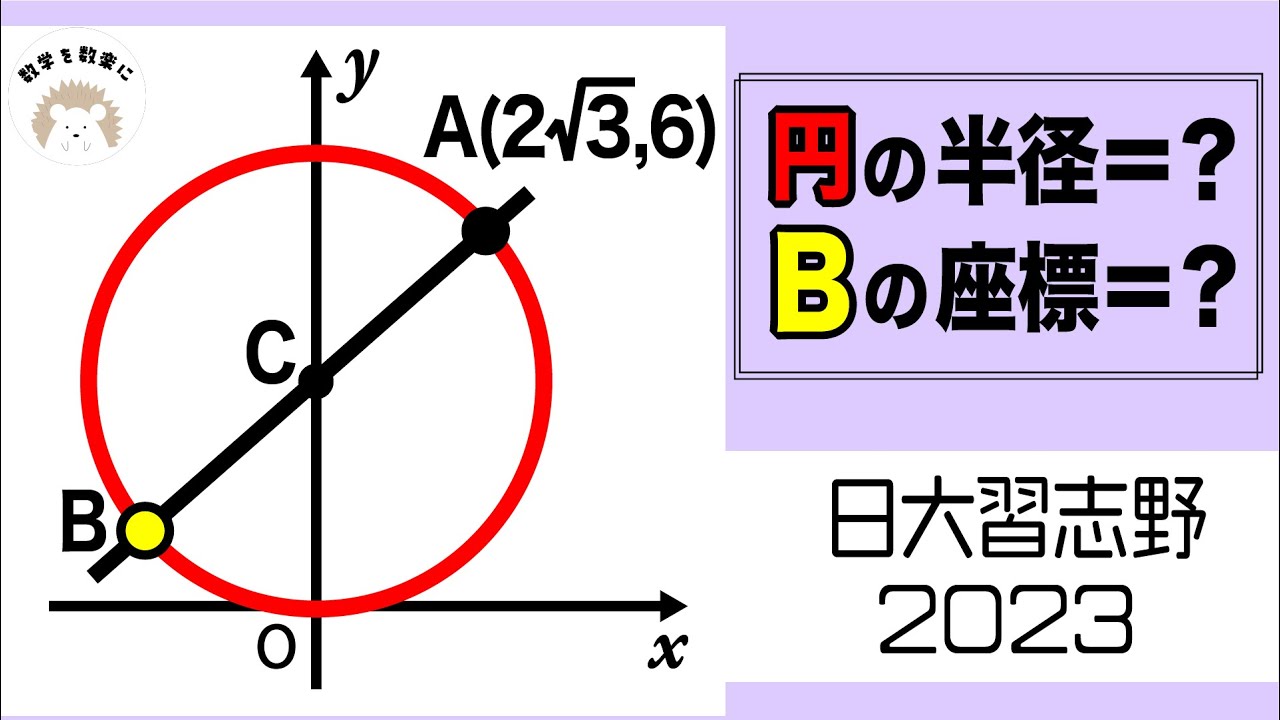
円の半径=?
Bの座標=?
*図は動画内参照
2023日本大学習志野高等学校(改)
この動画を見る
円の半径=?
Bの座標=?
*図は動画内参照
2023日本大学習志野高等学校(改)
これ何してる?

2023灘中最初の一問 計算

単元:
#算数(中学受験)#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#過去問解説(学校別)
指導講師:
数学を数楽に
問題文全文(内容文):
$2023 \times (\frac{1}{14} - \frac{1}{15}) \times \frac{1}{17} \times \frac{1}{17}$
= $1 \div (81-?)$
2023灘中学校
この動画を見る
$2023 \times (\frac{1}{14} - \frac{1}{15}) \times \frac{1}{17} \times \frac{1}{17}$
= $1 \div (81-?)$
2023灘中学校
2023高校入試解説10問目 二次方程式2023 日大習志野

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$x^2 - 6 \times 17x - 2023 = 0$
2023日本大学習志野高等学校
この動画を見る
2次方程式を解け
$x^2 - 6 \times 17x - 2023 = 0$
2023日本大学習志野高等学校
図で理解する2次方程式の解の公式~ほーみんに数学教えてみた~

単元:
#数学(中学生)#中3数学#2次方程式#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
図で理解する2次方程式の解の公式~ほーみんに数学教えてみた~
この動画を見る
図で理解する2次方程式の解の公式~ほーみんに数学教えてみた~
2023高校入試解説9問目 和と差の積は二乗の差 日大習志野

単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(1+\sqrt 2)(1+\sqrt 8)(1-\frac{1}{\sqrt 2})(1-\frac{1}{\sqrt 8})$
2023日本大学習志野高等学校
この動画を見る
$(1+\sqrt 2)(1+\sqrt 8)(1-\frac{1}{\sqrt 2})(1-\frac{1}{\sqrt 8})$
2023日本大学習志野高等学校
【中学数学】高校入試:2022年度神奈川県立高校入試数学大問5アイ
単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
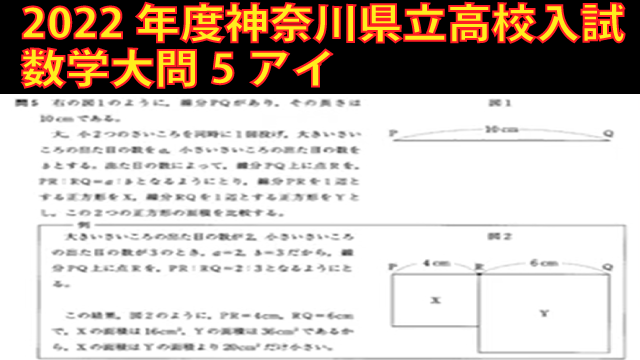
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(ア) Xの面積とYの面積が等しくなる確率は□である。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
この動画を見る
大,小2つのさいころを同時に1回投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとする。出た目の数によって,線分PQ上に点Rを,PR:RQ=a:bとなるようにとり,線分PRを1辺とする正方形をX,線分RQを1辺とする正方形をYとし,この2つの正方形の面積を比較する。
(ア) Xの面積とYの面積が等しくなる確率は□である。
(イ) Xの面積がYの面積より25cm²以上大きくなる確率は□である。
【スバラ式 解法!】因数分解:青雲高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ (2x+1)^2-3(x-1)(x+2)-27$を因数分解せよ.
青雲高校過去問
この動画を見る
$ (2x+1)^2-3(x-1)(x+2)-27$を因数分解せよ.
青雲高校過去問
【中学数学】円の中にある角度を求めよ~2022年神奈川公立高校入試~【高校受験】

単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
動画内の図において、5点$A,B,C,D,E$は円0の周上の点で、$BE//CD$であり、線分$AD$は$\angle BDE$の二等分線である。
また、点$F$は線分$AD$と線分$CE$との交点である。
このとき、$\angle AFE$を求めよ。
この動画を見る
動画内の図において、5点$A,B,C,D,E$は円0の周上の点で、$BE//CD$であり、線分$AD$は$\angle BDE$の二等分線である。
また、点$F$は線分$AD$と線分$CE$との交点である。
このとき、$\angle AFE$を求めよ。
【中学数学】二等辺三角形の性質の証明~定理を導く~【中2数学】

気分を高めて数学の入試問題を解答するキラキラ~全国入試問題解法 #Shorts #Sound #数学 #高校入試

単元:
#数学(中学生)#中1数学#正の数・負の数#方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2つの自然数$m,n$は
$ 2^m-1=(2n+1)(2n+3)$を満たす.
$ m=6$のとき,$n$の値を求めよ.
慶應義塾高校過去問
この動画を見る
2つの自然数$m,n$は
$ 2^m-1=(2n+1)(2n+3)$を満たす.
$ m=6$のとき,$n$の値を求めよ.
慶應義塾高校過去問
【方針が決まれば進むだけ!】整数:愛光高等学校~全国入試問題解法

単元:
#計算と数の性質#数学(中学生)#中1数学#正の数・負の数#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$168$と$1260$の最大公約数を$x$とする.
$ x$の正の約数をすべてかけ合わせると,$x^y$と表せる.
$x,y$をそれぞれ求めよ.
愛光高校過去問
この動画を見る
$168$と$1260$の最大公約数を$x$とする.
$ x$の正の約数をすべてかけ合わせると,$x^y$と表せる.
$x,y$をそれぞれ求めよ.
愛光高校過去問
三角形の辺と式の値の正負を調べる 大阪教育大附属平野

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,cが三角形の3辺の長さを表すとき$a^2-b^2-c^2+2bc$の正負を調べよ
大阪教育大学附属高等学校平野校舎(改)
この動画を見る
a,b,cが三角形の3辺の長さを表すとき$a^2-b^2-c^2+2bc$の正負を調べよ
大阪教育大学附属高等学校平野校舎(改)
【中学数学】円と接線の問題~2022年埼玉県公立高校入試~【高校受験】
単元:
#数学(中学生)#中1数学#平面図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
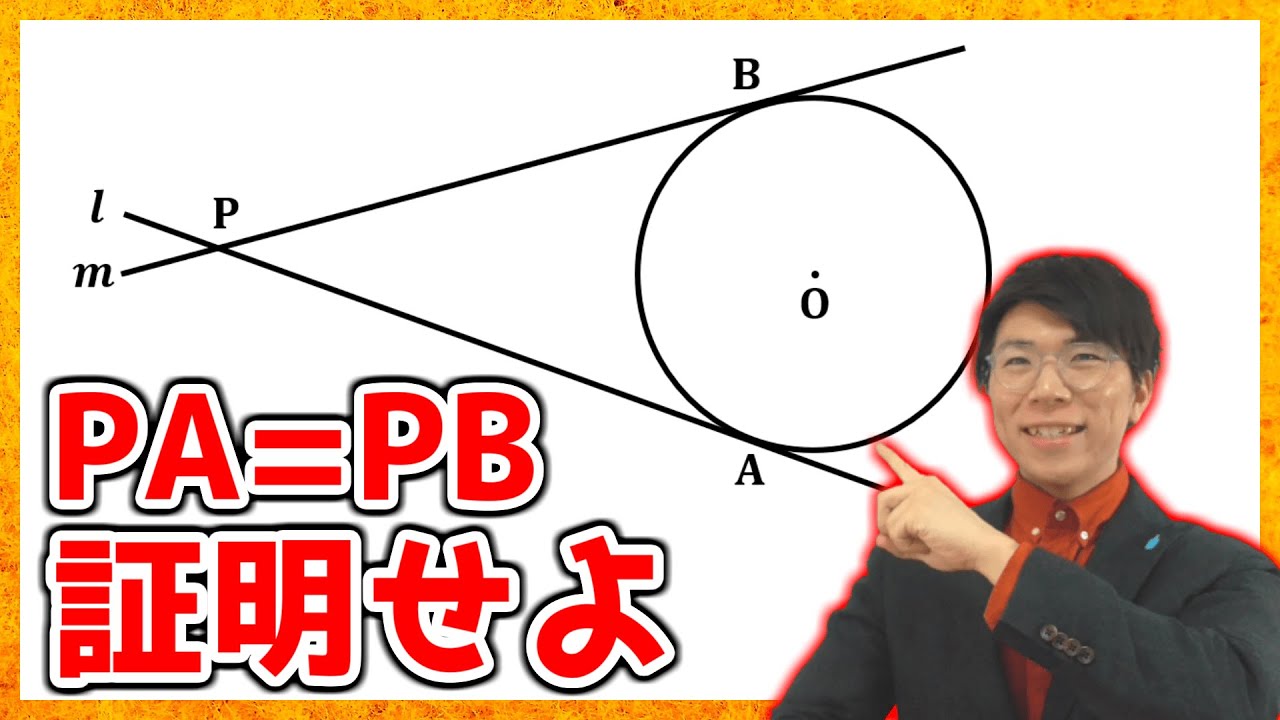
図のように点Oを中心とする円周上に2点A,Bをとり、A,Bを通る円Oの接線をそれぞれl,mとする。
直線lとmが点Pで交わるとき、PA = PBであることを証明せよ。
※図は動画内参照
この動画を見る
図のように点Oを中心とする円周上に2点A,Bをとり、A,Bを通る円Oの接線をそれぞれl,mとする。
直線lとmが点Pで交わるとき、PA = PBであることを証明せよ。
※図は動画内参照
正答率1%の問題

【中学数学】高校入試:2022年度神奈川県立高校入試数学大問4(ウ)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
2022年度神奈川県立高校入試数学大問4(ウ)解説していきます.
この動画を見る
2022年度神奈川県立高校入試数学大問4(ウ)解説していきます.
【中学数学】二等辺三角形になることの証明~問題演習~【中2数学】

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
三角形ABCは AB = AC の二等辺三角形である。
BD = CE なら三角形ADEが二等辺三角形になることを証明せよ。
※図は動画内参照
この動画を見る
三角形ABCは AB = AC の二等辺三角形である。
BD = CE なら三角形ADEが二等辺三角形になることを証明せよ。
※図は動画内参照
高校入試じゃないよ 中学入試だよ 2023西大和学園中
単元:
#算数(中学受験)#数学(中学生)#中2数学#過去問解説(学校別)#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
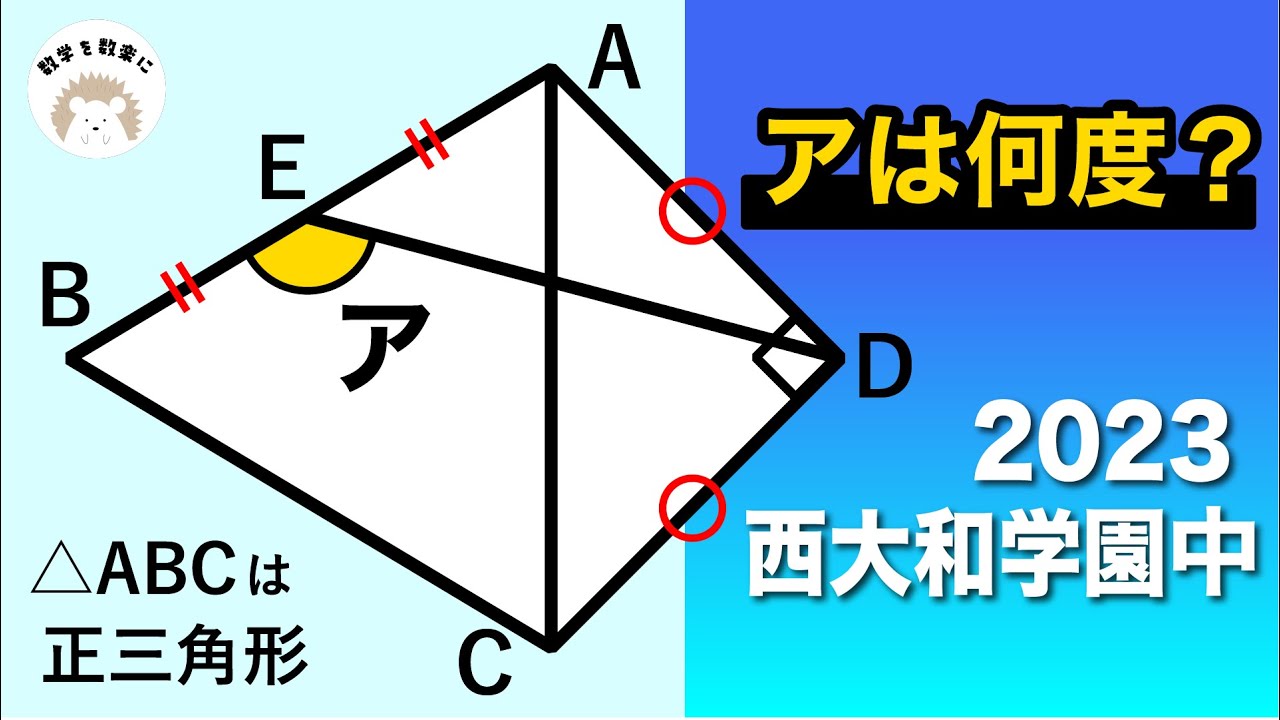
△ABCは正三角形
$\angle$アは何度?
*図は動画内参照
2023西大和学園中学校
この動画を見る
△ABCは正三角形
$\angle$アは何度?
*図は動画内参照
2023西大和学園中学校
2023高校入試解説8問目 内接円 西大和学園 内接円

単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC∽△PRQ
△PRQ=?
*図は動画内参照
2023西大和学園高等学校
この動画を見る
△ABC∽△PRQ
△PRQ=?
*図は動画内参照
2023西大和学園高等学校
2023高校入試解説7問目 工夫して解け2次方程式 早稲田佐賀

単元:
#数学(中学生)#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$(2x -1)^2 + 2x -57 = 0$
2023早稲田佐賀高等学校
この動画を見る
2次方程式を解け
$(2x -1)^2 + 2x -57 = 0$
2023早稲田佐賀高等学校
【ここは無理せず安全に!】因数分解:江戸川学園取手高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ a^2-4b^2+12bc-9c^2$を因数分解しなさい.
江戸川取手高校過去問
この動画を見る
$ a^2-4b^2+12bc-9c^2$を因数分解しなさい.
江戸川取手高校過去問
【中学数学】三角形の面積求めよ~2022年神奈川公立高校入試~【高校受験】

単元:
#数学(中学生)#中1数学#平面図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
図において、線分$AB$は円$O$の直径であり、2点$C,D$は円$O$の周上の点である。
また、点Eは線分$AC$上の点で、$BC//DE$であり、点$F$は線分$AB$と線分$DE$との交点である。
$AE=2cm,CE=1cm,DE=3cm$のとき、三角形$BDF$の面積を求めよ。
この動画を見る
図において、線分$AB$は円$O$の直径であり、2点$C,D$は円$O$の周上の点である。
また、点Eは線分$AC$上の点で、$BC//DE$であり、点$F$は線分$AB$と線分$DE$との交点である。
$AE=2cm,CE=1cm,DE=3cm$のとき、三角形$BDF$の面積を求めよ。
2023高校入試解説6問目 座標平面上の正三角形 西大和学園
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
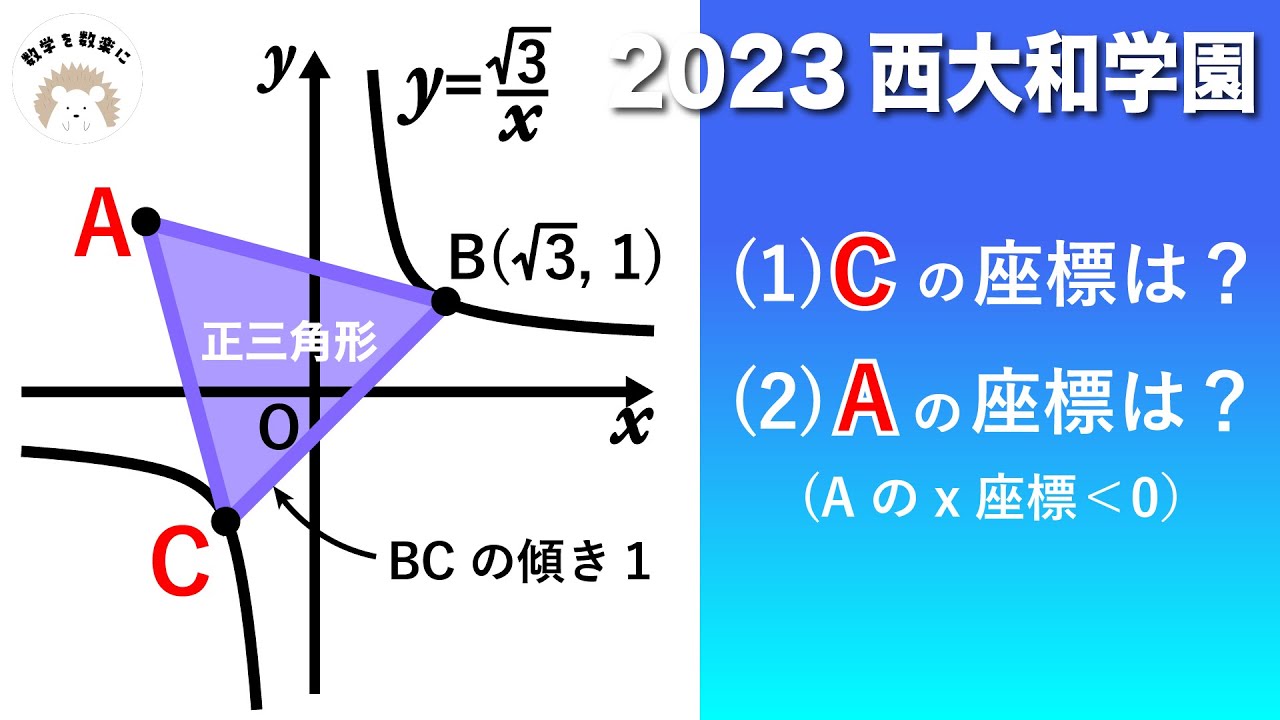
(1)Cの座標は?
(2)Aの座標は?
(Aのx座標<0)
*図は動画内参照
2023西大和学園高等学校
この動画を見る
(1)Cの座標は?
(2)Aの座標は?
(Aのx座標<0)
*図は動画内参照
2023西大和学園高等学校
