 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
【数学3分間!】関数:青雲高等学校~全国入試問題解法【とんとん♪】

単元:
#数学(中学生)#中3数学#高校入試過去問(数学)#青雲高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 青雲高等学校
【$x,y$:整数】
$[x,y]=\displaystyle \frac{3x+2y}{2x+3y}$
と定めるとき、
$\displaystyle \frac{[-2,2]+[10,-1]}{[4,3]-[20,-2]}$
の値を求めよ。
この動画を見る
入試問題 青雲高等学校
【$x,y$:整数】
$[x,y]=\displaystyle \frac{3x+2y}{2x+3y}$
と定めるとき、
$\displaystyle \frac{[-2,2]+[10,-1]}{[4,3]-[20,-2]}$
の値を求めよ。
【TikTok】扇形の面積を一瞬で求める

【中学数学】分数の割り算・多項式の計算~計算ミスをなくす方法~ 1-2【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$(12a^2-6a)\div \displaystyle \frac{2}{3}$
2⃣
$(\displaystyle \frac{2}{3}x^2y^2-\displaystyle \frac{4}{9}xy^2+2xy)\div(-\displaystyle \frac{2}{9}xy)$
3⃣
$(4x^3-6x^2+\displaystyle \frac{8}{5}x)\div(-\displaystyle \frac{4}{5}x)$
4⃣
$(-8a^2b+16ab)\div \displaystyle \frac{4}{5}a$
5⃣
$(4ab^2+5abc+\displaystyle \frac{1}{2})\div(\displaystyle \frac{7b}{5a})$
この動画を見る
1⃣
$(12a^2-6a)\div \displaystyle \frac{2}{3}$
2⃣
$(\displaystyle \frac{2}{3}x^2y^2-\displaystyle \frac{4}{9}xy^2+2xy)\div(-\displaystyle \frac{2}{9}xy)$
3⃣
$(4x^3-6x^2+\displaystyle \frac{8}{5}x)\div(-\displaystyle \frac{4}{5}x)$
4⃣
$(-8a^2b+16ab)\div \displaystyle \frac{4}{5}a$
5⃣
$(4ab^2+5abc+\displaystyle \frac{1}{2})\div(\displaystyle \frac{7b}{5a})$
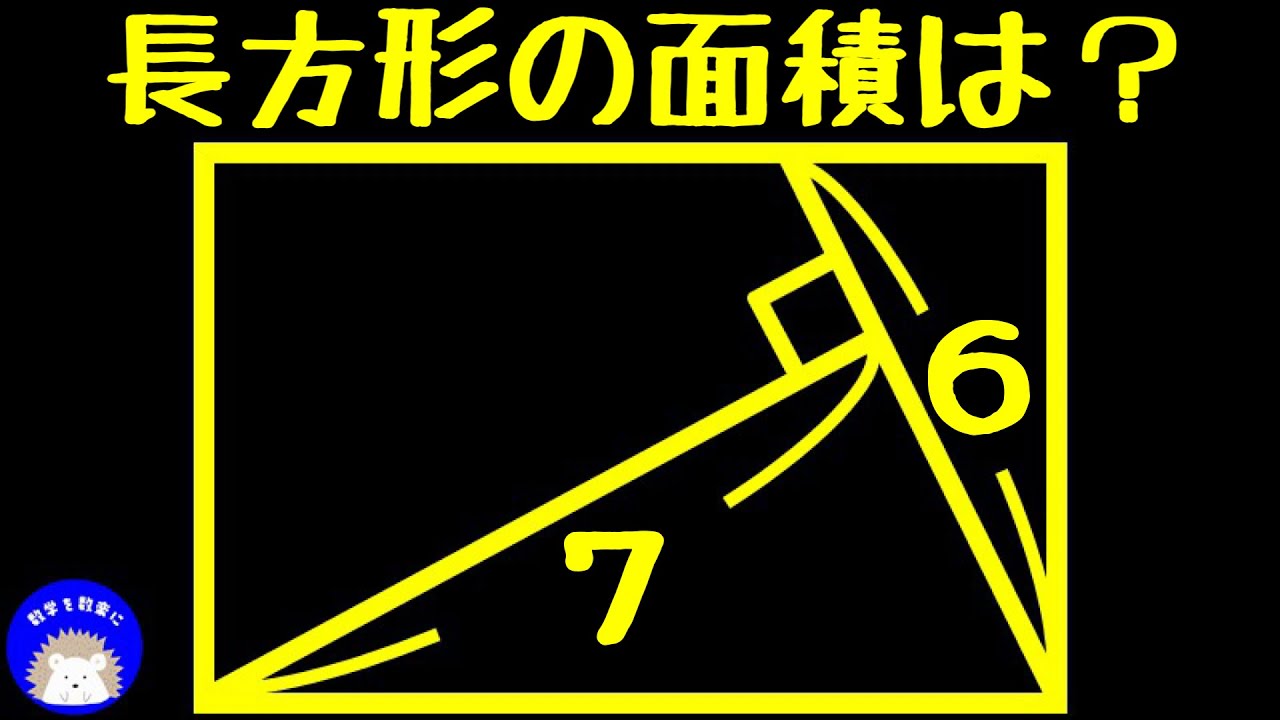
気付けば一瞬!!算数 長方形の面積=❓
【中学数学】因数分解の演習~一緒に解こう~ 1-6.5【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
$(x+3)-2(x+3)^2$
2⃣
$(x+y)^2-(x+y)-12$
3⃣
$x^2(a+b)-4x(a+b)+4(a+b)$
この動画を見る
1⃣
$(x+3)-2(x+3)^2$
2⃣
$(x+y)^2-(x+y)-12$
3⃣
$x^2(a+b)-4x(a+b)+4(a+b)$
中学受験算数 図形

因数分解 2通りの解説

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(x^2-15x)+(x^2-225)+(x^2+2x-255)$を因数分解せよ。
函館ラ・サール
この動画を見る
$(x^2-15x)+(x^2-225)+(x^2+2x-255)$を因数分解せよ。
函館ラ・サール
高校入試だけど3次方程式 動画内に誘導あり! 徳島文理(改)

単元:
#数学(中学生)#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^3+a^2-a-1$を因数分解
$(x+1)^3+(x+1)^2-x-2=0$を解け
徳島文理高等学校
この動画を見る
$a^3+a^2-a-1$を因数分解
$(x+1)^3+(x+1)^2-x-2=0$を解け
徳島文理高等学校
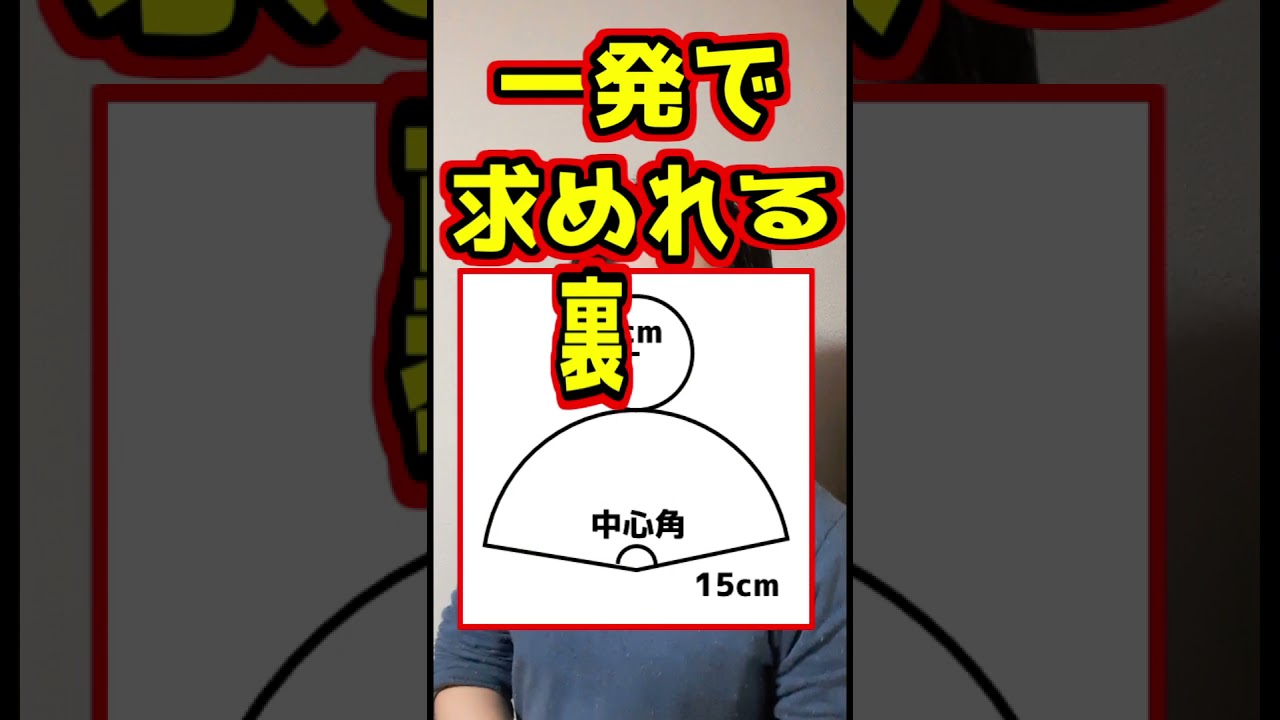
【TikTok】円錐の中心角の裏技
【3分で解ける!考える力倍増⁉】連立方程式:城北高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#城北高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 城北高等学校
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - y = \sqrt{ 5 } \\
x^2 - y^2 = 15
\end{array}
\right.
\end{eqnarray}$
この動画を見る
入試問題 城北高等学校
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - y = \sqrt{ 5 } \\
x^2 - y^2 = 15
\end{array}
\right.
\end{eqnarray}$
【中学数学】連立方程式割合の問題演習~2種類の解き方を教えます~ 2-3.5【中2数学】

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ある中学校の昨年の全校生徒数は男女合わせて220人でした。
今年は昨年と比べ、男子が5%増え、女子が2%減ったため、全体では4人増えました。
今年の男子と女子の人数をそれぞれ求めよ。
この動画を見る
ある中学校の昨年の全校生徒数は男女合わせて220人でした。
今年は昨年と比べ、男子が5%増え、女子が2%減ったため、全体では4人増えました。
今年の男子と女子の人数をそれぞれ求めよ。
中2数学「単項式の乗法と除法」【毎日配信】

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
例題
次の計算をしなさい.
(1)$2x\times 5y$
(2)$6a\times \left(-\dfrac{2}{3}b\right)$
(3)$(-3x^2)\times 4xy$
(4)$(-3ab)^2$
(5)$5x^2y\times (-2xy)^3$
(6)$15ab\div (-5ab)$
(7)$12m^2\div \dfrac{3}{4}m$
(8)$\left(-\dfrac{9}{8}a^2b\right)\div \dfrac{3}{4}ab$
(9)$\left(-\dfrac{9}{16}m^2n\right)\div \dfrac{3}{8}mn^2$
この動画を見る
例題
次の計算をしなさい.
(1)$2x\times 5y$
(2)$6a\times \left(-\dfrac{2}{3}b\right)$
(3)$(-3x^2)\times 4xy$
(4)$(-3ab)^2$
(5)$5x^2y\times (-2xy)^3$
(6)$15ab\div (-5ab)$
(7)$12m^2\div \dfrac{3}{4}m$
(8)$\left(-\dfrac{9}{8}a^2b\right)\div \dfrac{3}{4}ab$
(9)$\left(-\dfrac{9}{16}m^2n\right)\div \dfrac{3}{8}mn^2$
【TikTok】池の周りを回る問題の裏技

指数の計算 函館ラ・サール B
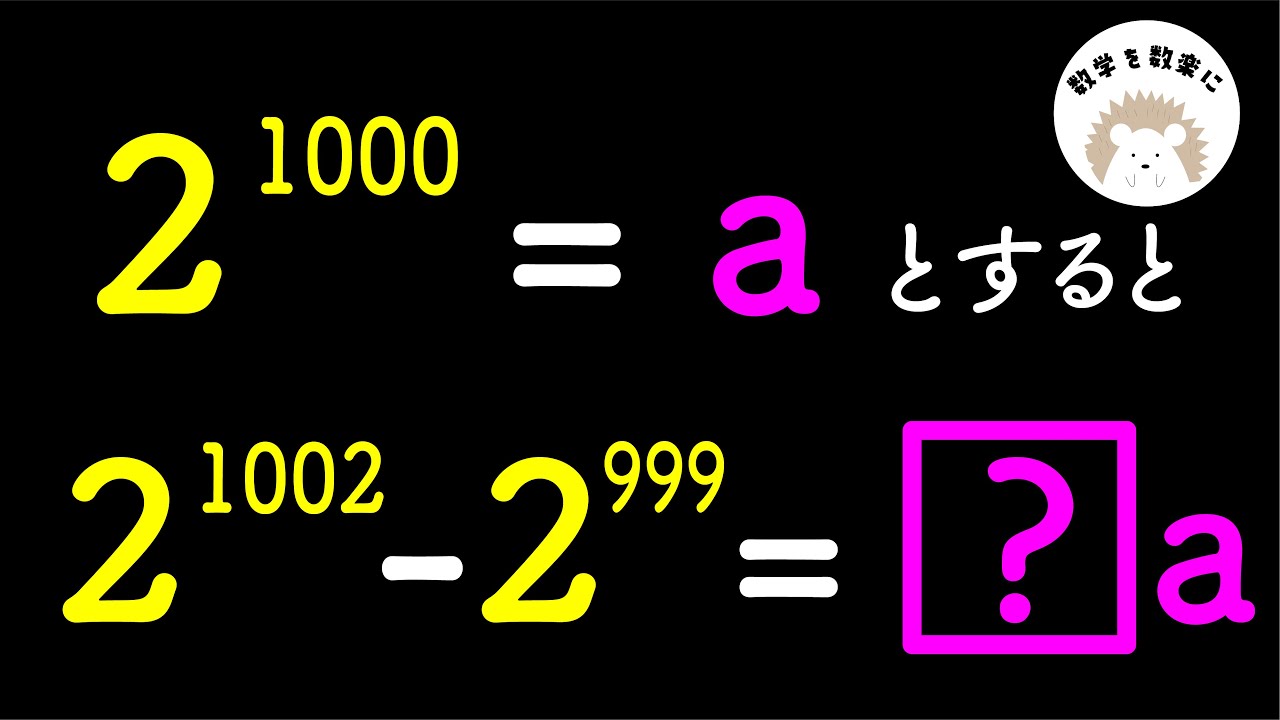
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{1000}=a$とすると
$2^{1002} - 2^{999}=\boxed{?}a$
函館ラ・サール
この動画を見る
$2^{1000}=a$とすると
$2^{1002} - 2^{999}=\boxed{?}a$
函館ラ・サール
【5分で3つの解法付き!】平方根:慶応義塾女子高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#慶應義塾女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 慶応義塾女子高等学校
次の式を計算しなさい。
$(\sqrt{ 5 }-\sqrt{ 2 }+1)(\sqrt{ 5 }+\sqrt{ 2 }+1)(\sqrt{ 5 }-2)$
この動画を見る
入試問題 慶応義塾女子高等学校
次の式を計算しなさい。
$(\sqrt{ 5 }-\sqrt{ 2 }+1)(\sqrt{ 5 }+\sqrt{ 2 }+1)(\sqrt{ 5 }-2)$
【中学数学】連立方程式の裏技の証明~式変形不要な解き方~ 2-4.5【中2数学】

整数問題 早稲田実業

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$c^2+4a^2+b^2 =65$を満たす正の整数a,b,cの組を求めよ。
早稲田実業学校
この動画を見る
$c^2+4a^2+b^2 =65$を満たす正の整数a,b,cの組を求めよ。
早稲田実業学校
中2数学「分数のいろいろな計算」【毎日配信】
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
例題
次の計算をしなさい.
(1)$\dfrac{1}{5}(2a-b)+\dfrac{1}{2}(-a+3b)$
(2)$\dfrac{1}{4}(3x-y)-\dfrac{1}{3}(x-5y)$
(3)$\dfrac{2a-b}{3}+\dfrac{a+4b}{2}$
(4)$\dfrac{x-3y}{4}-\dfrac{2x-y}{3}$
この動画を見る
例題
次の計算をしなさい.
(1)$\dfrac{1}{5}(2a-b)+\dfrac{1}{2}(-a+3b)$
(2)$\dfrac{1}{4}(3x-y)-\dfrac{1}{3}(x-5y)$
(3)$\dfrac{2a-b}{3}+\dfrac{a+4b}{2}$
(4)$\dfrac{x-3y}{4}-\dfrac{2x-y}{3}$
【ひるむな!5分で計算力up!】文字式:関西学院高等部~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#関西学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 関西学院高等部
次の式を計算せよ。
$(\displaystyle \frac{c}{3a^2})^3 \div (-\displaystyle \frac{b^2c^3}{1.5a})^3 \times (-4ab^3c^5)^2$
この動画を見る
入試問題 関西学院高等部
次の式を計算せよ。
$(\displaystyle \frac{c}{3a^2})^3 \div (-\displaystyle \frac{b^2c^3}{1.5a})^3 \times (-4ab^3c^5)^2$
素因数分解 教えて下さい たくさんのコメントありがとうございます。

中2数学「多項式の分配法則」【毎日配信】

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
例題
次の計算をしなさい.
(1)$3(x+5y)$
(2)$\left(\dfrac{x}{4}-\dfrac{y}{3}\right)\times 12$
(3)$(10a-15b)\div 5$
(4)$(4x+20y-12)\div \left(-\dfrac{4}{5}\right)$
(5)$3(x+2y)+2(2x-5y)$
(6)$6(2a-3b)-5(3a-2b)$
この動画を見る
例題
次の計算をしなさい.
(1)$3(x+5y)$
(2)$\left(\dfrac{x}{4}-\dfrac{y}{3}\right)\times 12$
(3)$(10a-15b)\div 5$
(4)$(4x+20y-12)\div \left(-\dfrac{4}{5}\right)$
(5)$3(x+2y)+2(2x-5y)$
(6)$6(2a-3b)-5(3a-2b)$
因数分解 伝えたいことはただ一つ

【裏技】二等分線の〇●の角度の裏技です

【3分でスッキリ!一度は解きたい!】平方根:秋田県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#秋田県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 秋田県の公立高等学校
$N \leqq \sqrt{ n } \lt N + 1$
上式を満たす $n$が31個あるとき、 $N$の値を求めなさい
【$n$、$N$:自然数】
この動画を見る
入試問題 秋田県の公立高等学校
$N \leqq \sqrt{ n } \lt N + 1$
上式を満たす $n$が31個あるとき、 $N$の値を求めなさい
【$n$、$N$:自然数】
3択問題 理由も考えよう 帝塚山泉ヶ丘
単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
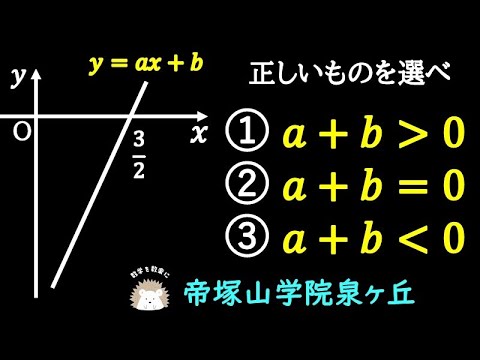
正しいものを選べ
① a+b>0
② a+b=0
③ a+B<0
*図は動画内参照
帝塚山泉ヶ丘高等学校
この動画を見る
正しいものを選べ
① a+b>0
② a+b=0
③ a+B<0
*図は動画内参照
帝塚山泉ヶ丘高等学校
【裏ワザ?5分間!】二次関数:鹿児島県公立高等学校~全国入試問題解法【神授業】
単元:
#数学(中学生)#2次関数#高校入試過去問(数学)#鹿児島県公立高校入試#鹿児島県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
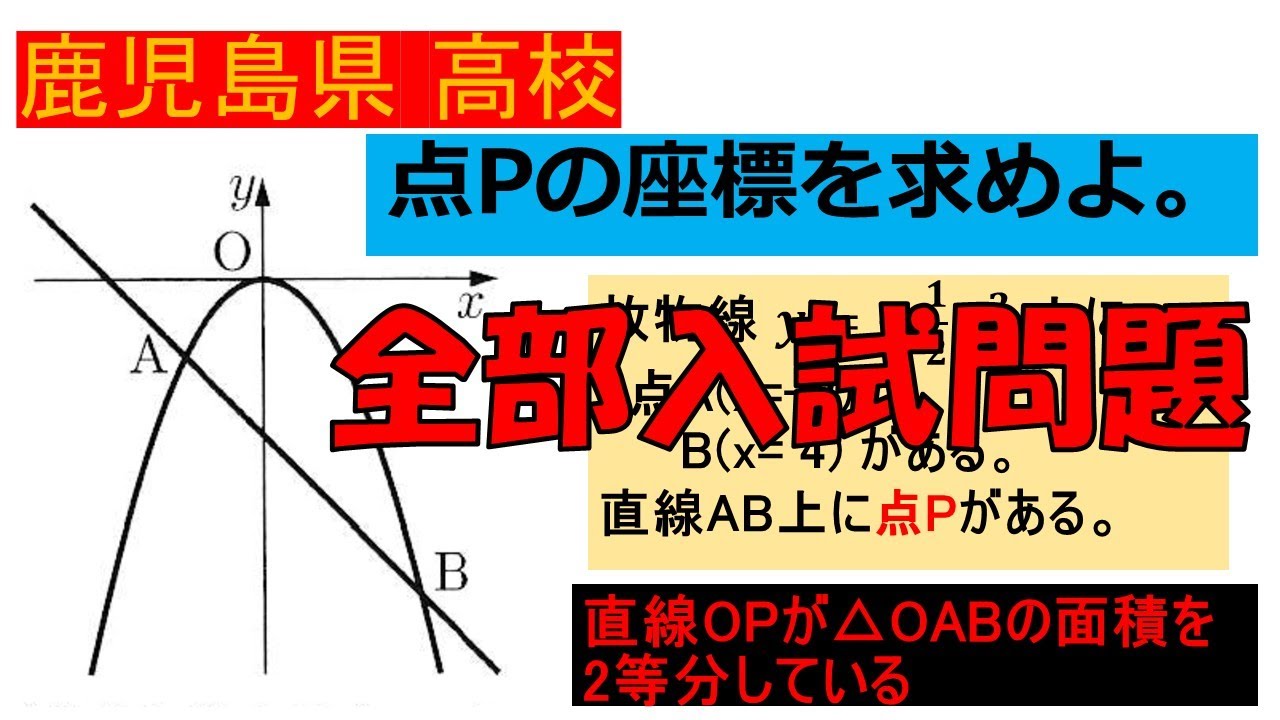
入試問題 鹿児島県の公立高等学校
点Pの座標を求めよ。
放物線 $y=\displaystyle \frac{1}{2}x^2$上に
2点$A(x=-2) B(x= 4)$がある。
直線$AB$上に点$P$がある。
直線$OP$が$\triangle OAB$の面積を 2等分している。
※図は動画内参照
この動画を見る
入試問題 鹿児島県の公立高等学校
点Pの座標を求めよ。
放物線 $y=\displaystyle \frac{1}{2}x^2$上に
2点$A(x=-2) B(x= 4)$がある。
直線$AB$上に点$P$がある。
直線$OP$が$\triangle OAB$の面積を 2等分している。
※図は動画内参照
言いたいことはただ一つ

中2数学「同類項・式の加法と減法」【毎日配信】

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
中学受験算数・高校受験数学けいたくチャンネル
問題文全文(内容文):
例1
次の計算をしなさい.
(1)$4a-3b-a+5b$
(2)$x^2-3x+2x^2+5x$
(3)$3ab-2a-ab+a$
(4)$\dfrac{x}{6}+\dfrac{y}{3}+\dfrac{y}{4}-\dfrac{x}{9}$
例2
(1)$(4x-y)+(x+5y)$
(2)$(3x+7y)-(2x-5y)$
(3)$(2x^2+5x-1)-(3-4x^2+x)$
(4)
$\begin{array}{r}
3x-2y \\[0.5pt]
\underline{+\phantom{0}2x+5y}\\[-3pt]
\\[-3pt]
\end{array}$
(5)
$\begin{array}{r}
-2x+5y-4 \\[0.5pt]
\underline{-\phantom{0}-5x-3y+6}\\[-3pt]
\\[-3pt]
\end{array}$
この動画を見る
例1
次の計算をしなさい.
(1)$4a-3b-a+5b$
(2)$x^2-3x+2x^2+5x$
(3)$3ab-2a-ab+a$
(4)$\dfrac{x}{6}+\dfrac{y}{3}+\dfrac{y}{4}-\dfrac{x}{9}$
例2
(1)$(4x-y)+(x+5y)$
(2)$(3x+7y)-(2x-5y)$
(3)$(2x^2+5x-1)-(3-4x^2+x)$
(4)
$\begin{array}{r}
3x-2y \\[0.5pt]
\underline{+\phantom{0}2x+5y}\\[-3pt]
\\[-3pt]
\end{array}$
(5)
$\begin{array}{r}
-2x+5y-4 \\[0.5pt]
\underline{-\phantom{0}-5x-3y+6}\\[-3pt]
\\[-3pt]
\end{array}$
楽々解こう!
式の値 慶應女子 B
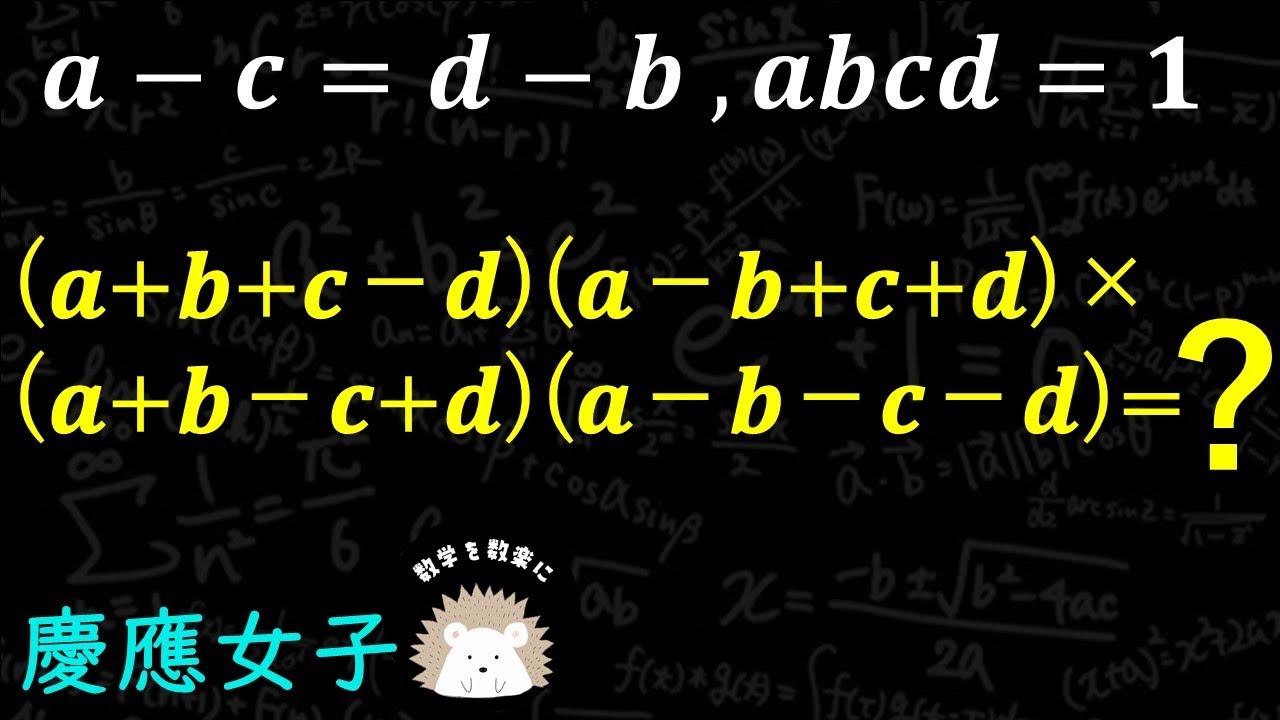
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a-c=d-b,abcd=1のとき
(a+b+c-d)(a-b+c+d)(a+b-c+d)(a-b-c-d)
慶應義塾女子高等学校
この動画を見る
a-c=d-b,abcd=1のとき
(a+b+c-d)(a-b+c+d)(a+b-c+d)(a-b-c-d)
慶應義塾女子高等学校
