数学検定準1級
数学検定準1級
#6数検準1級2次過去問 x軸回転体
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#接線と増減表・最大値・最小値#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{7}$
$0\leqq x\leqq 2\pi$
$f(x)=\sin x+\sqrt3\cos x+x$
(1)$f(x)$の最大値,最小値を求めよ.
(2)$y=f(x),x$軸,$y$軸$x=2\pi$で囲まれた図形を
$x$軸中心に回転した体積$V$を求めよ.
この動画を見る
$\boxed{7}$
$0\leqq x\leqq 2\pi$
$f(x)=\sin x+\sqrt3\cos x+x$
(1)$f(x)$の最大値,最小値を求めよ.
(2)$y=f(x),x$軸,$y$軸$x=2\pi$で囲まれた図形を
$x$軸中心に回転した体積$V$を求めよ.
#5数検準1級1次過去問 指数
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
3^{x+1}-2･3^y=-9 \\
\log_2 (x+1)-\log_2 (y+2)=-1
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
3^{x+1}-2･3^y=-9 \\
\log_2 (x+1)-\log_2 (y+2)=-1
\end{array}
\right.
\end{eqnarray}$
#4数検準1級1次（過去問）
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#式と証明#整式の除法・分数式・二項定理#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$2a_n-S_n=2^n$
一般項$a_n$を求めよ.
この動画を見る
$2a_n-S_n=2^n$
一般項$a_n$を求めよ.
練習問題17 教採用数検準1級2次の練習問題（関数列の極限）
単元：
#数学検定・数学甲子園・数学オリンピック等#数列#数列とその和（等差・等比・階差・Σ）#関数と極限#数列の極限#その他#数学検定#数学検定準1級#数学(高校生)#数B#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$x\neq 1\ f_1(x)=\dfrac{1}{(x-1)^2}$
$f_1(x)=x \ f_{n-1} \ (x)+n$と定めるとき,
$\displaystyle \lim_{n\to\infty} \dfrac{f_n (e^{\frac{1}{n}})}{n^2}$これを解け.
この動画を見る
$x\neq 1\ f_1(x)=\dfrac{1}{(x-1)^2}$
$f_1(x)=x \ f_{n-1} \ (x)+n$と定めるとき,
$\displaystyle \lim_{n\to\infty} \dfrac{f_n (e^{\frac{1}{n}})}{n^2}$これを解け.
#3 数検準1級2次過去問 三角関数
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}$
$\tan \alpha=k,-\dfrac{\pi}{2}\lt \alpha \lt \dfrac{\pi}{2}$をみたす
$\alpha$を$T(k)$で表す
(1)$xy\neq 1$のとき,
$ \\\ \tan (T(x)+T(y))$
(2)$4T\left(\dfrac{1}{5}\right)-T\left(\dfrac{1}{239}\right)=\dfrac{\pi}{4}$を示せ.
＊$-\dfrac{\pi}{2} \lt \beta\lt \dfrac{\pi}{2}$は利用してよい.
この動画を見る
$\boxed{1}$
$\tan \alpha=k,-\dfrac{\pi}{2}\lt \alpha \lt \dfrac{\pi}{2}$をみたす
$\alpha$を$T(k)$で表す
(1)$xy\neq 1$のとき,
$ \\\ \tan (T(x)+T(y))$
(2)$4T\left(\dfrac{1}{5}\right)-T\left(\dfrac{1}{239}\right)=\dfrac{\pi}{4}$を示せ.
＊$-\dfrac{\pi}{2} \lt \beta\lt \dfrac{\pi}{2}$は利用してよい.
重積分⑥-3【曲面・平面で囲まれた体積】（高専数学 微積II，数検1級1次解析対応）
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a\gt 0$とする.
曲面$Z=4a^2-x^2-y^2$と
$xy$平面で囲まれた体積$V$を求めよ.
この動画を見る
$a\gt 0$とする.
曲面$Z=4a^2-x^2-y^2$と
$xy$平面で囲まれた体積$V$を求めよ.
#2 数検準1級1次過去問 数列
単元：
#数学検定・数学甲子園・数学オリンピック等#数列#数列とその和（等差・等比・階差・Σ）#数学検定#数学検定準1級#数学(高校生)#数B
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}$
$2a_n-S_n=2^n$
一般鋼$a_n$を求めよ.
この動画を見る
$\boxed{3}$
$2a_n-S_n=2^n$
一般鋼$a_n$を求めよ.
練習問題9（数検準1級 教員採用試験 極限値からの区分求積法）【難】
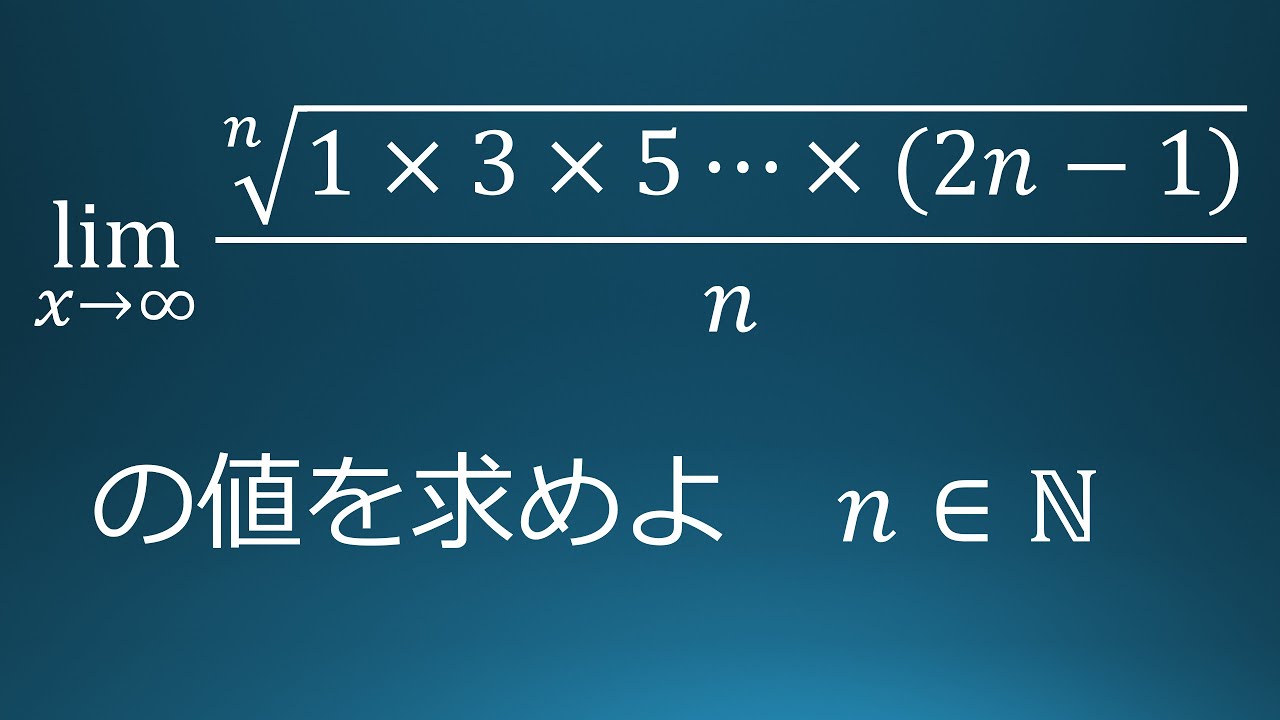
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
限値からの区分求積法を解説していきます.
この動画を見る
限値からの区分求積法を解説していきます.
練習問題8（数検準1級 教員採用試験 極限値からの区分求積法）
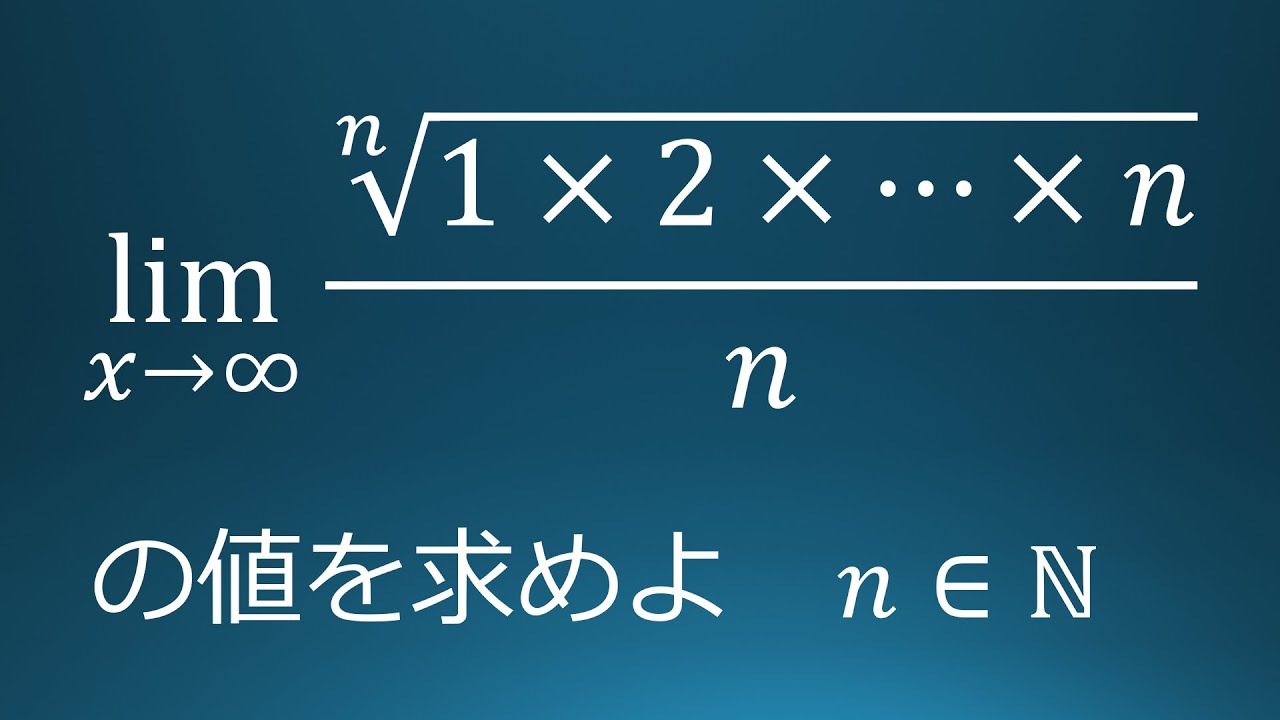
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty} \dfrac{\sqrt[n]{1\times 3\times 5\times ･･･ \times(2n-1)}}{n}$
これを解け.
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{\sqrt[n]{1\times 3\times 5\times ･･･ \times(2n-1)}}{n}$
これを解け.
練習問題7（数検準1級 教員採用試験 極限値）
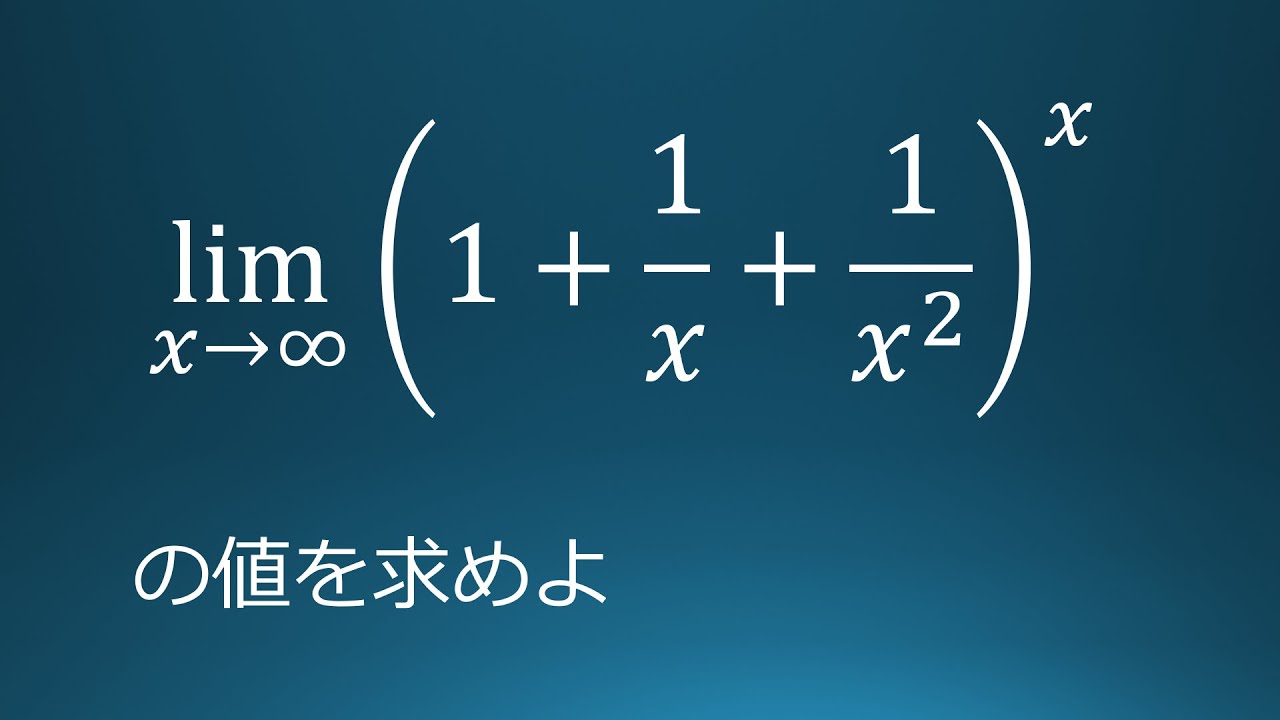
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to\infty} \left(1+\dfrac{1}{x}+\dfrac{1}{x^2}\right)^x$
これを解け.
この動画を見る
$\displaystyle \lim_{x\to\infty} \left(1+\dfrac{1}{x}+\dfrac{1}{x^2}\right)^x$
これを解け.
練習問題6（数検準1級 教員採用試験 極限値【やや難】）
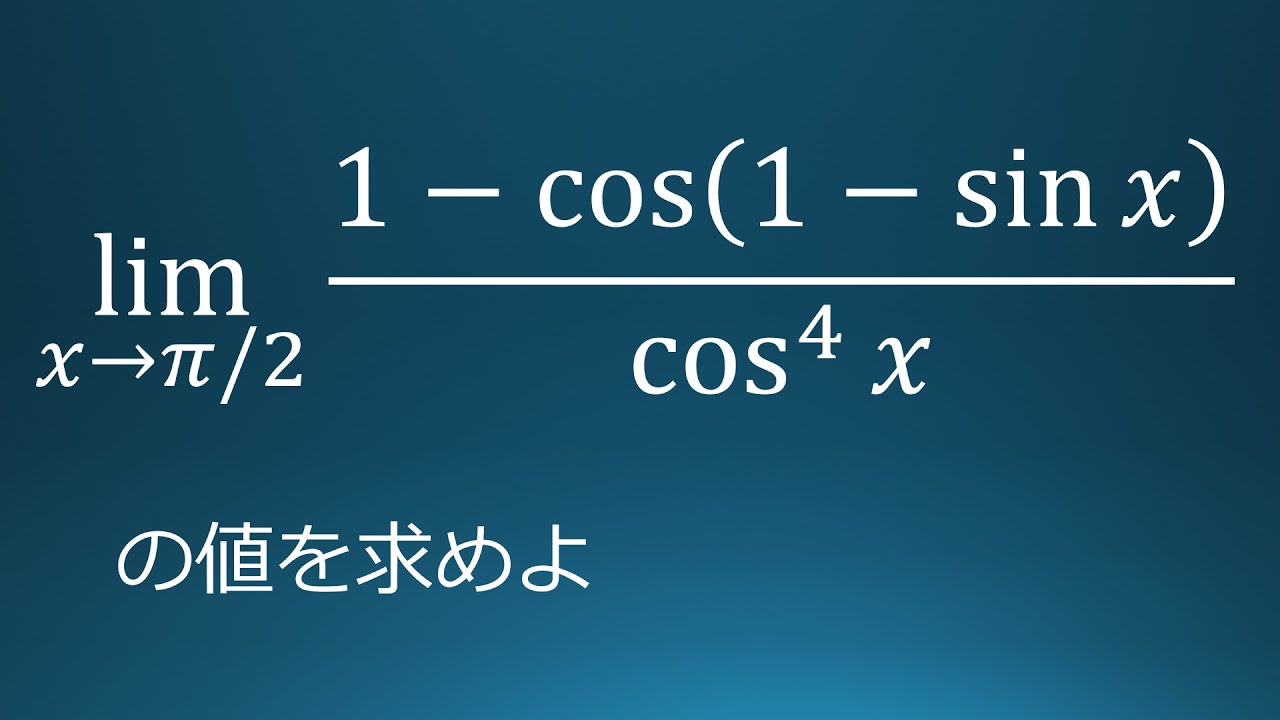
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to\frac{\pi}{2}} \dfrac{1-\cos(1-\sin x)}{\cos^4x}$
これを解け.
この動画を見る
$\displaystyle \lim_{x\to\frac{\pi}{2}} \dfrac{1-\cos(1-\sin x)}{\cos^4x}$
これを解け.
練習問題5（数検準1級 教員採用試験 極限値）
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#その他#数学検定#数学検定準1級#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to\infty} \dfrac{\tan^3x-\sin^3x}{x^5}$
これを解け.
この動画を見る
$\displaystyle \lim_{x\to\infty} \dfrac{\tan^3x-\sin^3x}{x^5}$
これを解け.
数検準1級2次（5番 整数問題）
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}$ 5以上の任意の素数$p$に対して,$p^2$を$n$で割ると1余る.
最大の自然数$n$を求めよ.
①$n\leftarrow IN$
$n^2=3k$ or $3k+1 (^3k\Leftarrow IN)$
②$5\leqq p:係数$
$p=6k\pm 1 (^3k\Leftarrow IN)$
この動画を見る
$\boxed{5}$ 5以上の任意の素数$p$に対して,$p^2$を$n$で割ると1余る.
最大の自然数$n$を求めよ.
①$n\leftarrow IN$
$n^2=3k$ or $3k+1 (^3k\Leftarrow IN)$
②$5\leqq p:係数$
$p=6k\pm 1 (^3k\Leftarrow IN)$
数検準1級2次（7番 回転体の体積）
単元：
#数学検定・数学甲子園・数学オリンピック等#立体図形#体積・表面積・回転体・水量・変化のグラフ#数学検定#数学検定準1級
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{7}$ $c:y=\dfrac{x}{\sqrt{1+x^2}} \quad (0\leqq x\leqq 1)$
(1)$c,x=1$,$x$軸で囲まれた図形を$x$軸中心に回転させた体積$V$を求めよ.
(2)$c,y=\dfrac{1}{\sqrt2},y$軸で囲まれた図形を$y$軸中心に回転させた体積$V_2$を求めよ.
この動画を見る
$\boxed{7}$ $c:y=\dfrac{x}{\sqrt{1+x^2}} \quad (0\leqq x\leqq 1)$
(1)$c,x=1$,$x$軸で囲まれた図形を$x$軸中心に回転させた体積$V$を求めよ.
(2)$c,y=\dfrac{1}{\sqrt2},y$軸で囲まれた図形を$y$軸中心に回転させた体積$V_2$を求めよ.
数検準1級2次（4番 行列）
単元：
#数学検定・数学甲子園・数学オリンピック等#数列#数列とその和（等差・等比・階差・Σ）#数学検定#数学検定準1級#数学(高校生)#数B
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{4}$ $A=\dbinom{a \quad b}{ c\quad d },A^2=\theta $
$kE-A$が逆行列をもつための必要十分条件を求めよ.
この動画を見る
$\boxed{4}$ $A=\dbinom{a \quad b}{ c\quad d },A^2=\theta $
$kE-A$が逆行列をもつための必要十分条件を求めよ.
数検準1級2次（3番 極限値）
単元：
#数学検定・数学甲子園・数学オリンピック等#関数と極限#関数の極限#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}$
曲線$y=2\sqrt x$上の点$P(t,2\sqrt t)$に対して,
$y$軸上に$OP=OQ$をみたす点$Q$をとる.
直線$PQ$と$x$軸との支点を$R$とする.
$\displaystyle \lim_{t\to 0} \ OR$を求めよ.
図は動画内参照
この動画を見る
$\boxed{3}$
曲線$y=2\sqrt x$上の点$P(t,2\sqrt t)$に対して,
$y$軸上に$OP=OQ$をみたす点$Q$をとる.
直線$PQ$と$x$軸との支点を$R$とする.
$\displaystyle \lim_{t\to 0} \ OR$を求めよ.
図は動画内参照
数検準1級2次（2番 数列、Σの公式）
単元：
#数学検定・数学甲子園・数学オリンピック等#数列#数列とその和（等差・等比・階差・Σ）#数学検定#数学検定準1級#数学(高校生)#数B
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{2}$ $S_n=\left(\dfrac{n}{6}(n+1)(2n+1)\right)^2$
(1)一般項$a_n$を求めよ.
(2)$\displaystyle \sum_{k=1}^n k^5$を求めよ.
この動画を見る
$\boxed{2}$ $S_n=\left(\dfrac{n}{6}(n+1)(2n+1)\right)^2$
(1)一般項$a_n$を求めよ.
(2)$\displaystyle \sum_{k=1}^n k^5$を求めよ.
数検準1級2次（1番 三角関数）
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}$ $0\lt \alpha,\beta,\varUpsilon \lt \dfrac{\pi}{2}$
$\tan \alpha=\dfrac{1}{2},\tan\beta=\dfrac{1}{5},\tan\varUpsilon=\dfrac{1}{8}$のとき,
$\sin(\alpha+\beta+\varUpsilon)$と,$\cos(\alpha+\beta+\varUpsilon)$
の大小を比較せよ.
この動画を見る
$\boxed{1}$ $0\lt \alpha,\beta,\varUpsilon \lt \dfrac{\pi}{2}$
$\tan \alpha=\dfrac{1}{2},\tan\beta=\dfrac{1}{5},\tan\varUpsilon=\dfrac{1}{8}$のとき,
$\sin(\alpha+\beta+\varUpsilon)$と,$\cos(\alpha+\beta+\varUpsilon)$
の大小を比較せよ.
数検準1級1次（6番 双曲線）
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定準1級
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{6}$双曲線$x^2-y^2=2$の焦点の座標を求めよ.
この動画を見る
$\boxed{6}$双曲線$x^2-y^2=2$の焦点の座標を求めよ.
数検準1級1次（5番 積分）
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#不定積分・定積分#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}$これを解け.
(1)$\displaystyle \int_{}^{} \dfrac{1}{x^2\ e^{\frac{1}{x}}}$
(2)$\displaystyle \int_{\frac{1}{2}}^{1}\dfrac{1}{x^2\ e^{\frac{1}{2}}}$
この動画を見る
$\boxed{5}$これを解け.
(1)$\displaystyle \int_{}^{} \dfrac{1}{x^2\ e^{\frac{1}{x}}}$
(2)$\displaystyle \int_{\frac{1}{2}}^{1}\dfrac{1}{x^2\ e^{\frac{1}{2}}}$
数検準1級1次（7番 極限値）
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{7}$ $\displaystyle \lim_{x\to 0}\ \dfrac{1}{x}\left(\frac{1}{\sin x}-\dfrac{1}{\tan x}\right)$
これを解け.
この動画を見る
$\boxed{7}$ $\displaystyle \lim_{x\to 0}\ \dfrac{1}{x}\left(\frac{1}{\sin x}-\dfrac{1}{\tan x}\right)$
これを解け.
数検準1級1次（4番 複素数）
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{4}$複素数$Z=\dfrac{\sqrt3}{2}-\dfrac{1}{2}i$である.
(1)$Z$の偏角$\theta$を求めよ.
(2)$Z^5+\dfrac{1}{Z^5}$の値を求めよ.
この動画を見る
$\boxed{4}$複素数$Z=\dfrac{\sqrt3}{2}-\dfrac{1}{2}i$である.
(1)$Z$の偏角$\theta$を求めよ.
(2)$Z^5+\dfrac{1}{Z^5}$の値を求めよ.
数検準1級1次（3番 ベクトル）
単元：
#数学検定・数学甲子園・数学オリンピック等#平面上のベクトル#数学検定#数学検定準1級#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}$ $\vert \overrightarrow{ a }\vert=\vert \overrightarrow{ b }\vert,\vert \overrightarrow{ c }\vert=1$
$\vert \overrightarrow{ a }\vert \perp \vert \overrightarrow{ b }\vert,\vert \overrightarrow{ b }\vert \perp \vert \overrightarrow{ c }\vert,\vert \overrightarrow{ c }\vert \perp \vert \overrightarrow{ a}\vert$のとき,
$\vert \overrightarrow{ x }\vert=\vert \overrightarrow{ a }\vert+2\vert \overrightarrow{ b }\vert+3\vert \overrightarrow{ c }\vert$
$\vert \overrightarrow{ y }\vert=3\vert \overrightarrow{ a }\vert+\vert \overrightarrow{ b }\vert-2\vert \overrightarrow{ c }\vert$
のなす角$\theta$に対して$\cos\theta$の値を求めよ.
この動画を見る
$\boxed{3}$ $\vert \overrightarrow{ a }\vert=\vert \overrightarrow{ b }\vert,\vert \overrightarrow{ c }\vert=1$
$\vert \overrightarrow{ a }\vert \perp \vert \overrightarrow{ b }\vert,\vert \overrightarrow{ b }\vert \perp \vert \overrightarrow{ c }\vert,\vert \overrightarrow{ c }\vert \perp \vert \overrightarrow{ a}\vert$のとき,
$\vert \overrightarrow{ x }\vert=\vert \overrightarrow{ a }\vert+2\vert \overrightarrow{ b }\vert+3\vert \overrightarrow{ c }\vert$
$\vert \overrightarrow{ y }\vert=3\vert \overrightarrow{ a }\vert+\vert \overrightarrow{ b }\vert-2\vert \overrightarrow{ c }\vert$
のなす角$\theta$に対して$\cos\theta$の値を求めよ.
数検準1級1次（2番 等比数列）
単元：
#数学検定・数学甲子園・数学オリンピック等#数列#数列とその和（等差・等比・階差・Σ）#数学検定#数学検定準1級#数学(高校生)#数B
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{2}$実数の列$1,a,b,c,9$が,
この順で等比数列のとき,$a$の値を求めよ.
この動画を見る
$\boxed{2}$実数の列$1,a,b,c,9$が,
この順で等比数列のとき,$a$の値を求めよ.
数検準1級1次（1番 整式の計算）
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#式の計算（整式・展開・因数分解）#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}$ $x^8+x^4+1$を$x^2+x+1$で割ったときの商を求めよ.
この動画を見る
$\boxed{1}$ $x^8+x^4+1$を$x^2+x+1$で割ったときの商を求めよ.
数検準1級2次過去問【2020年12月】5番：整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$boxed{5}$ $m,n\in IN$とする.
(1)$100!=2^m \times (奇数)$と表したときの$m$の値を求めよ.
(2)$50!=n^2\times (互いに異なる素数の積)$と表したときの
素因数分解した形で表せ.
この動画を見る
$boxed{5}$ $m,n\in IN$とする.
(1)$100!=2^m \times (奇数)$と表したときの$m$の値を求めよ.
(2)$50!=n^2\times (互いに異なる素数の積)$と表したときの
素因数分解した形で表せ.
数検準1級2次過去問【2020年12月】4番：軌跡と焦点
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#図形と方程式#軌跡と領域#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{4}$点$(1,0)$からの距離と
直線$y=2$からの距離の比が$1:2$である点$P$の軌跡の焦点をすべて求めよ.
図は動画内参照
この動画を見る
$\boxed{4}$点$(1,0)$からの距離と
直線$y=2$からの距離の比が$1:2$である点$P$の軌跡の焦点をすべて求めよ.
図は動画内参照
数検準1級1次過去問【2020年12月】2番：三角関数
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{2}$ $\sin\theta+\cos\theta=\dfrac{1}{3}$のとき,
$\sin^3\theta+\cos^3\theta$の値を求めよ.
この動画を見る
$\boxed{2}$ $\sin\theta+\cos\theta=\dfrac{1}{3}$のとき,
$\sin^3\theta+\cos^3\theta$の値を求めよ.
数検準1級1次過去問【2020年12月】4番：複素数
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{4} \alpha=-2+i$で,$\beta=-3-i$である.これを解け.
(1)$\left| \dfrac{\alpha}{\beta} \right|$を求めよ.
(2)$\left( -\frac{\alpha}{\beta} \right)^{45}$の偏角$\theta$を求めよ.
$(0\leqq \theta \lt 2\pi)$
この動画を見る
$\boxed{4} \alpha=-2+i$で,$\beta=-3-i$である.これを解け.
(1)$\left| \dfrac{\alpha}{\beta} \right|$を求めよ.
(2)$\left( -\frac{\alpha}{\beta} \right)^{45}$の偏角$\theta$を求めよ.
$(0\leqq \theta \lt 2\pi)$
数検準1級1次過去問【2020年12月】3番：三角形の面積（ベクトル）
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#図形と計量#三角比への応用（正弦・余弦・面積）#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}$ $0(0,0,0),A(-2,1,1)B(-1,2,0)$を頂点に持つ
$\triangle{OAB}$の面積$S$を求めよ.
この動画を見る
$\boxed{3}$ $0(0,0,0),A(-2,1,1)B(-1,2,0)$を頂点に持つ
$\triangle{OAB}$の面積$S$を求めよ.