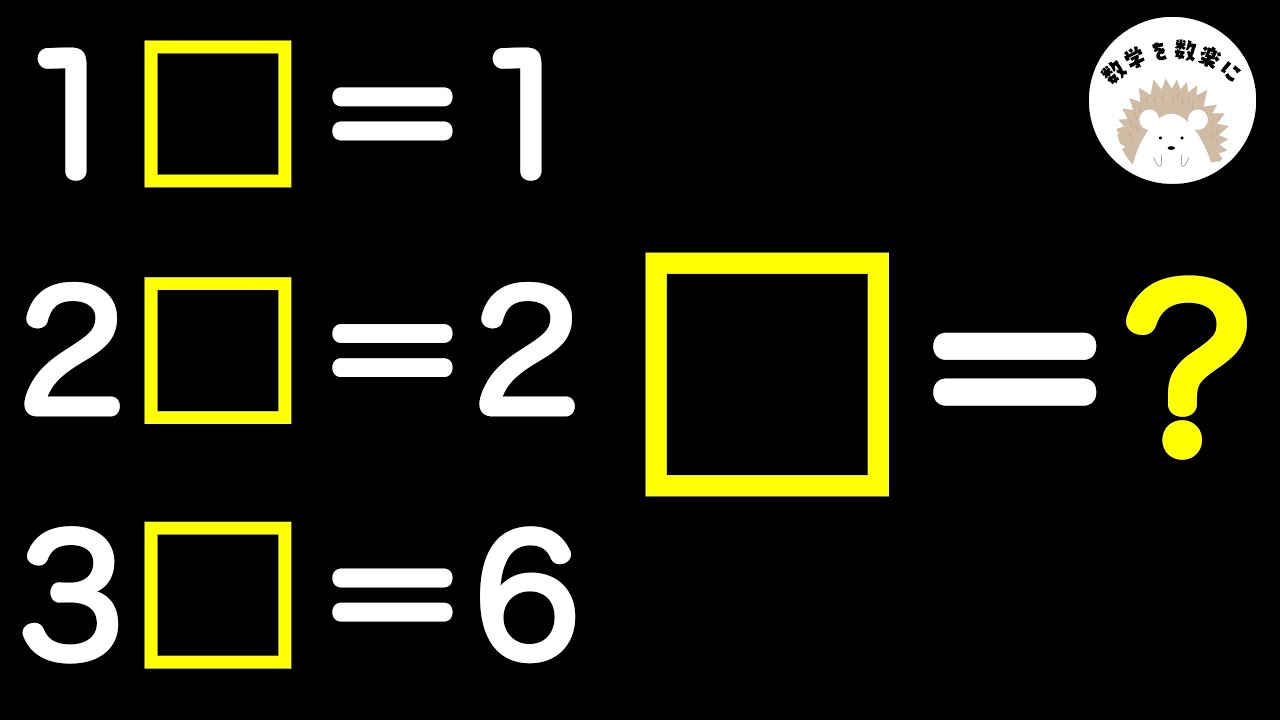問題文全文(内容文):
$\boxed{2}$ $a_1=10,a_{n+1}=\sqrt[5]{a_n}$である.
(1)一般項$a_n$を求めよ.
(2)$P_n=a_1 \times \cdots \times a_n$を求めよ.
$\boxed{2}$ $a_1=10,a_{n+1}=\sqrt[5]{a_n}$である.
(1)一般項$a_n$を求めよ.
(2)$P_n=a_1 \times \cdots \times a_n$を求めよ.
単元:
#数学検定・数学甲子園・数学オリンピック等#数列#数列とその和(等差・等比・階差・Σ)#数学検定#数学検定準1級#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$ $a_1=10,a_{n+1}=\sqrt[5]{a_n}$である.
(1)一般項$a_n$を求めよ.
(2)$P_n=a_1 \times \cdots \times a_n$を求めよ.
$\boxed{2}$ $a_1=10,a_{n+1}=\sqrt[5]{a_n}$である.
(1)一般項$a_n$を求めよ.
(2)$P_n=a_1 \times \cdots \times a_n$を求めよ.
投稿日:2020.12.15