問題文全文(内容文):
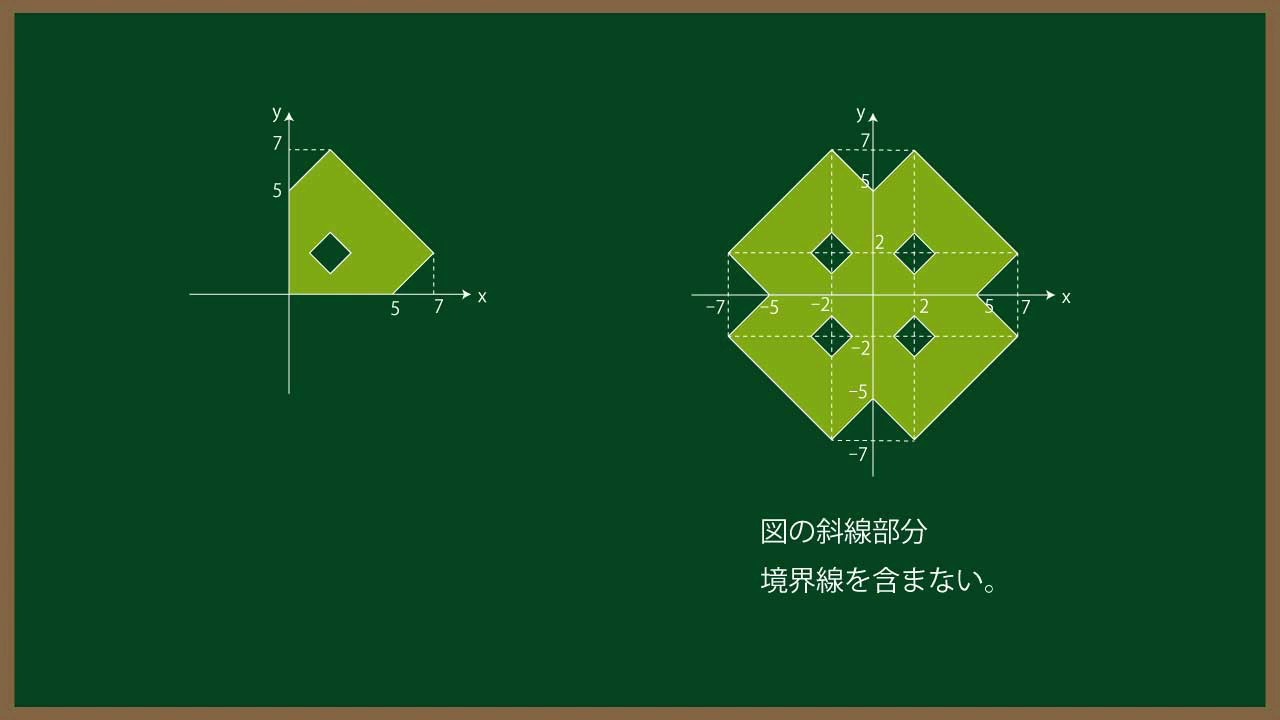
$\Large\boxed{4}$ 座標平面上の点(0,1)を中心として半径1の円を$C$とする。点P($x$,$y$)が$y$≧0の範囲にあり、PからCまでの最短距離は$ay$であるとする。ただし$a$は0<$a$<1を満たす定数である。このとき、次の問いに答えよ。
(1)点Pが円$C$の円周上または外部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(2)点Pが円$C$の円周上または内部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(3)$x$=$\displaystyle\frac{1}{2}$かつ0≦$y$≦2を満たす点P($x$,$y$)がちょうど3個存在するような定数$a$の範囲を求めよ。
$\Large\boxed{4}$ 座標平面上の点(0,1)を中心として半径1の円を$C$とする。点P($x$,$y$)が$y$≧0の範囲にあり、PからCまでの最短距離は$ay$であるとする。ただし$a$は0<$a$<1を満たす定数である。このとき、次の問いに答えよ。
(1)点Pが円$C$の円周上または外部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(2)点Pが円$C$の円周上または内部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(3)$x$=$\displaystyle\frac{1}{2}$かつ0≦$y$≦2を満たす点P($x$,$y$)がちょうど3個存在するような定数$a$の範囲を求めよ。
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面上の点(0,1)を中心として半径1の円を$C$とする。点P($x$,$y$)が$y$≧0の範囲にあり、PからCまでの最短距離は$ay$であるとする。ただし$a$は0<$a$<1を満たす定数である。このとき、次の問いに答えよ。
(1)点Pが円$C$の円周上または外部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(2)点Pが円$C$の円周上または内部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(3)$x$=$\displaystyle\frac{1}{2}$かつ0≦$y$≦2を満たす点P($x$,$y$)がちょうど3個存在するような定数$a$の範囲を求めよ。
$\Large\boxed{4}$ 座標平面上の点(0,1)を中心として半径1の円を$C$とする。点P($x$,$y$)が$y$≧0の範囲にあり、PからCまでの最短距離は$ay$であるとする。ただし$a$は0<$a$<1を満たす定数である。このとき、次の問いに答えよ。
(1)点Pが円$C$の円周上または外部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(2)点Pが円$C$の円周上または内部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(3)$x$=$\displaystyle\frac{1}{2}$かつ0≦$y$≦2を満たす点P($x$,$y$)がちょうど3個存在するような定数$a$の範囲を求めよ。
投稿日:2023.10.20