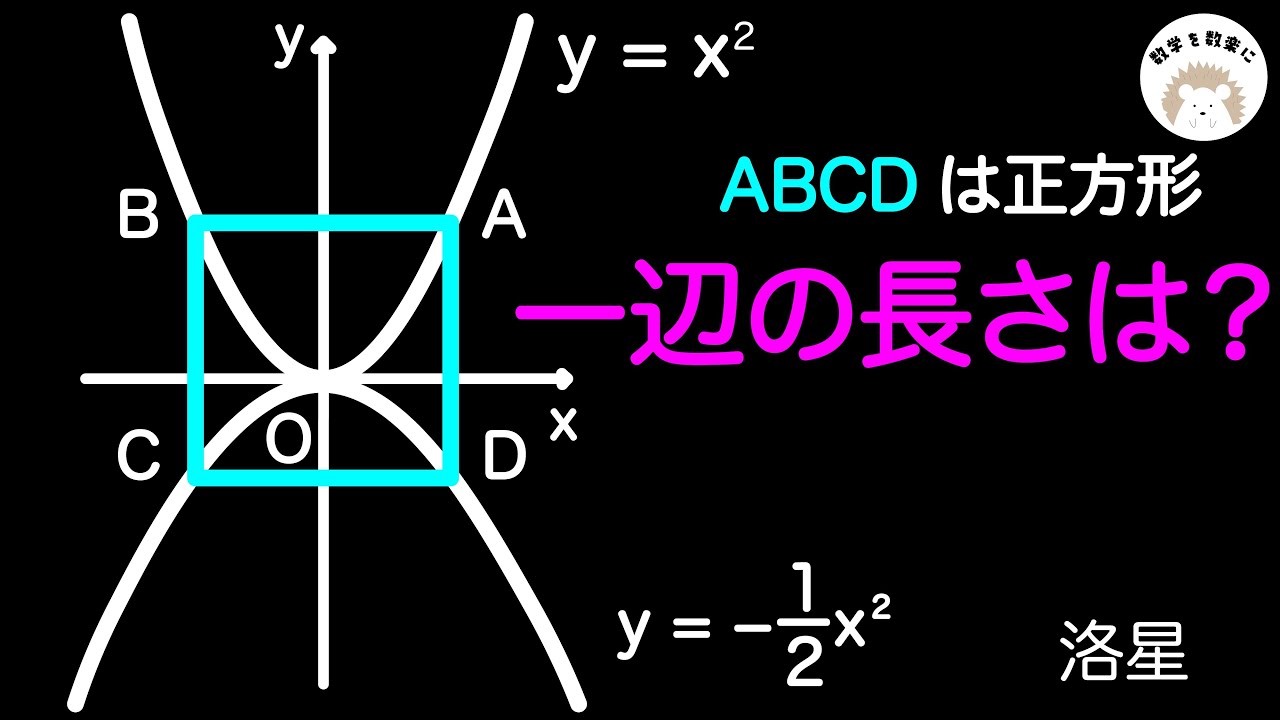
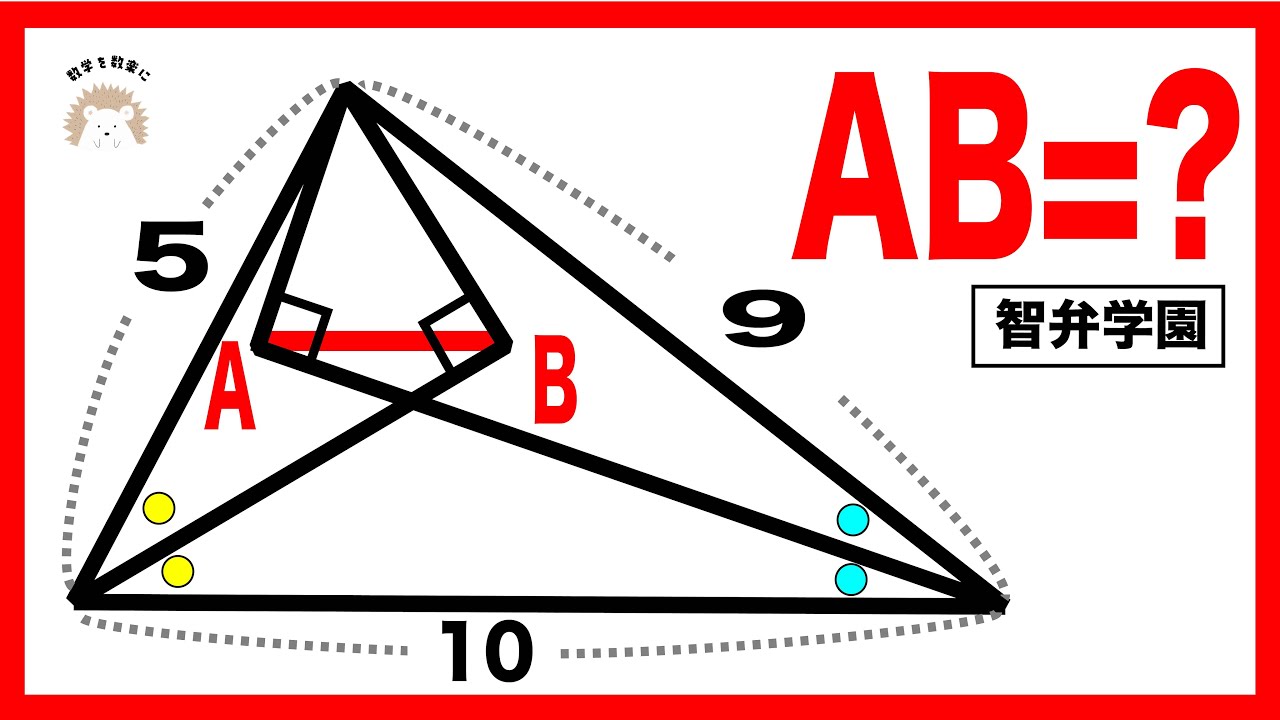
問題文全文(内容文):
$\angle A=90°,\angle B=60°$である直角三角形ABCにおいて、
その内接円の中心をO、半径をrとおく。また$a=BC$とする。
(1)rをaで表せ。
(2)次の条件を満たす負でない整数k,l,m,nの組を一つ求めよ。
$OA:OB=1:k+\sqrt{l}, OA:OC=1:m+\sqrt{n}$
2022北海道大学文系過去問
$\angle A=90°,\angle B=60°$である直角三角形ABCにおいて、
その内接円の中心をO、半径をrとおく。また$a=BC$とする。
(1)rをaで表せ。
(2)次の条件を満たす負でない整数k,l,m,nの組を一つ求めよ。
$OA:OB=1:k+\sqrt{l}, OA:OC=1:m+\sqrt{n}$
2022北海道大学文系過去問
単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
$\angle A=90°,\angle B=60°$である直角三角形ABCにおいて、
その内接円の中心をO、半径をrとおく。また$a=BC$とする。
(1)rをaで表せ。
(2)次の条件を満たす負でない整数k,l,m,nの組を一つ求めよ。
$OA:OB=1:k+\sqrt{l}, OA:OC=1:m+\sqrt{n}$
2022北海道大学文系過去問
$\angle A=90°,\angle B=60°$である直角三角形ABCにおいて、
その内接円の中心をO、半径をrとおく。また$a=BC$とする。
(1)rをaで表せ。
(2)次の条件を満たす負でない整数k,l,m,nの組を一つ求めよ。
$OA:OB=1:k+\sqrt{l}, OA:OC=1:m+\sqrt{n}$
2022北海道大学文系過去問
投稿日:2022.04.01