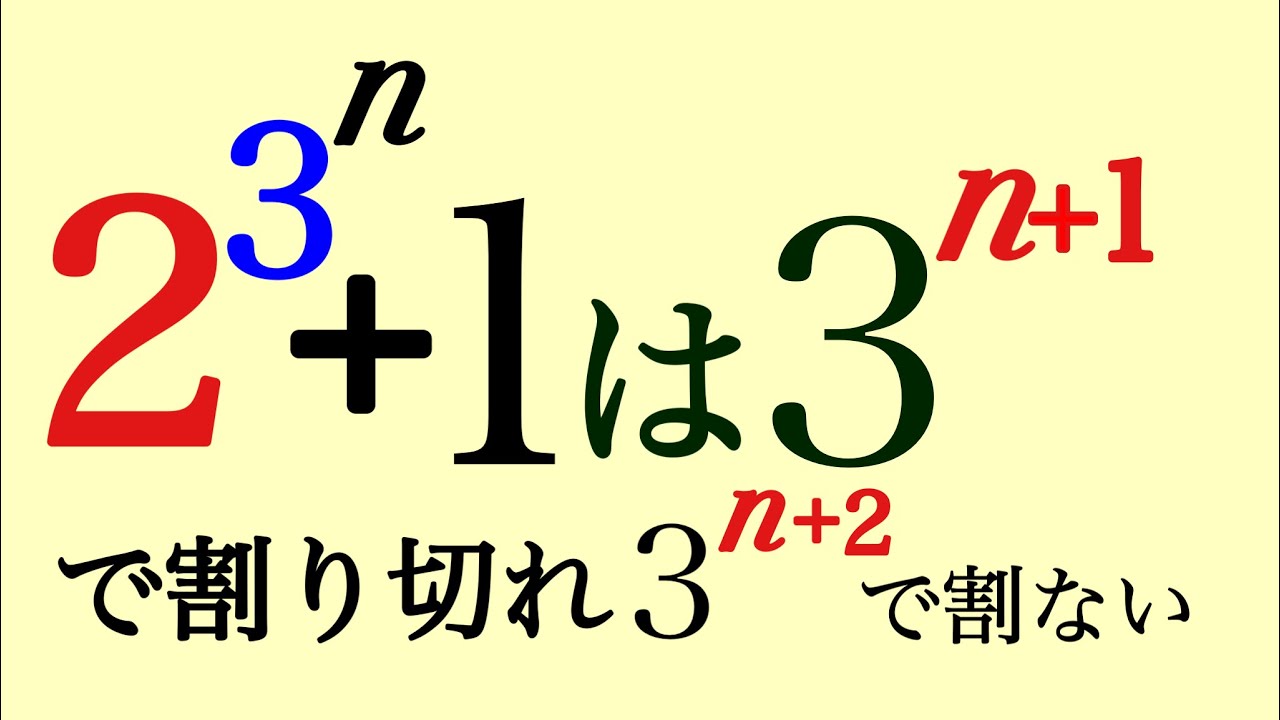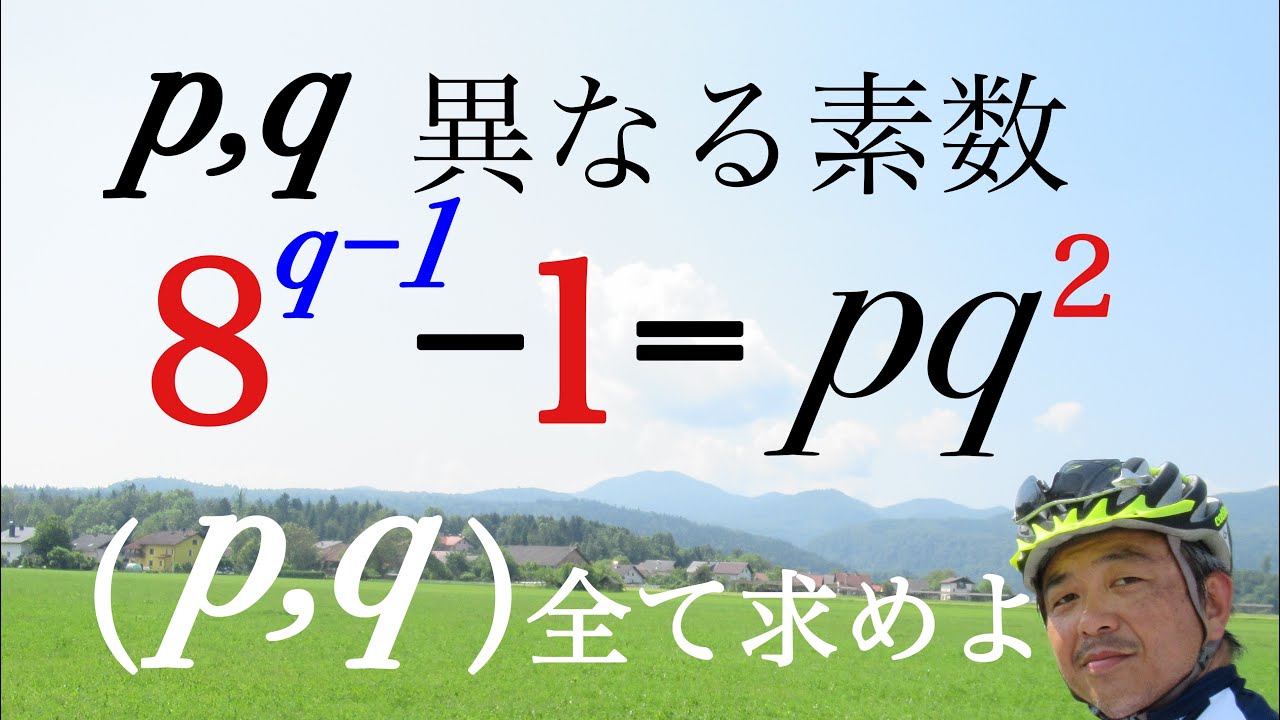【整数問題】素数を扱う難問！２通りで解説！【奈良県立医科大学】 - 質問解決D.B.（データベース）
Generic selectors
完全一致検索
タイトルから検索
記事本文から検索
Post Type Selectors
all_unit_post
質問解決D.B.（データベース） > 動画投稿 > 数学(高校生) > 数A > 整数の性質 > 約数・倍数・整数の割り算と余り・合同式 > 【整数問題】素数を扱う難問！２通りで解説！【奈良県立医科大学】

【整数問題】素数を扱う難問！２通りで解説！【奈良県立医科大学】

問題文全文(内容文)：
aを2以上の整数、pを2より大きい素数とする。ある正の整数kに対して等式a^p-1 -1=p^kが成り立つのは、a=2,p=3のみであることを示せ。
チャプター：

00:00 導入部分
00:45 【解法１】n乗-n乗で因数分解
07:52 【解法２】〇〇に着目してから因数分解

単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師： 数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
aを2以上の整数、pを2より大きい素数とする。ある正の整数kに対して等式a^p-1 -1=p^kが成り立つのは、a=2,p=3のみであることを示せ。
投稿日：2024.12.23

＜関連動画＞

福田の数学〜慶應義塾大学2024年薬学部第1問(5)〜整数解と素数の性質

アイキャッチ画像
単元： #数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師： 福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (5)自然数$a$,$b$と素数$p$は等式
$a^4$－$4a^2b$+$4b^3$－$b^4$=$p^2$
を満たす。このとき、数の組($a$,$b$,$p$)を全て求めると($a$,$b$,$p$)$\boxed{\ \ シ\ \ }$である。
この動画を見る　

【数A】整数の性質：φ関数（φ210とφ1050））

アイキャッチ画像
単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師： 理数個別チャンネル
問題文全文(内容文)：
φ(210)とφ(1050）を求めよ
この動画を見る　

【数A】整数の性質：合同式②　a,bは3で割り切れない整数とする。このとき、a⁴+a²b²+b⁴は3で割り切れることを証明せよ。

アイキャッチ画像
単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師： 理数個別チャンネル
問題文全文(内容文)：
a,bは3で割り切れない整数とする。このとき、$a^4+a^2b^2+b^4$は3で割り切れることを証明せよ。
この動画を見る　

福田のおもしろ数学310〜累乗で表された数の大小比較

アイキャッチ画像
単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師： 福田次郎
問題文全文(内容文)：
$$\left( \left( 3 \right)^3 \right)^4,\left( \left( 3 \right)^4 \right)^3,\left( \left( 3 \right)^4\right)^4,\left( \left( 4\right)^3 \right)^3,\left( \left( 4 \right)^3 \right)^4を昇順に直してください。ただし、a^{ b^c}=a^{ (b^c)}とする。$$
この動画を見る　

整数問題　昭和学院秀英

アイキャッチ画像
単元： #数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師： 数学を数楽に
問題文全文(内容文)：
n+7が11の倍数でn+11が7の倍数となる正の整数nの中で最小となるnの値を求めよ。
2024昭和学院秀英高等学校
この動画を見る　
Back to top