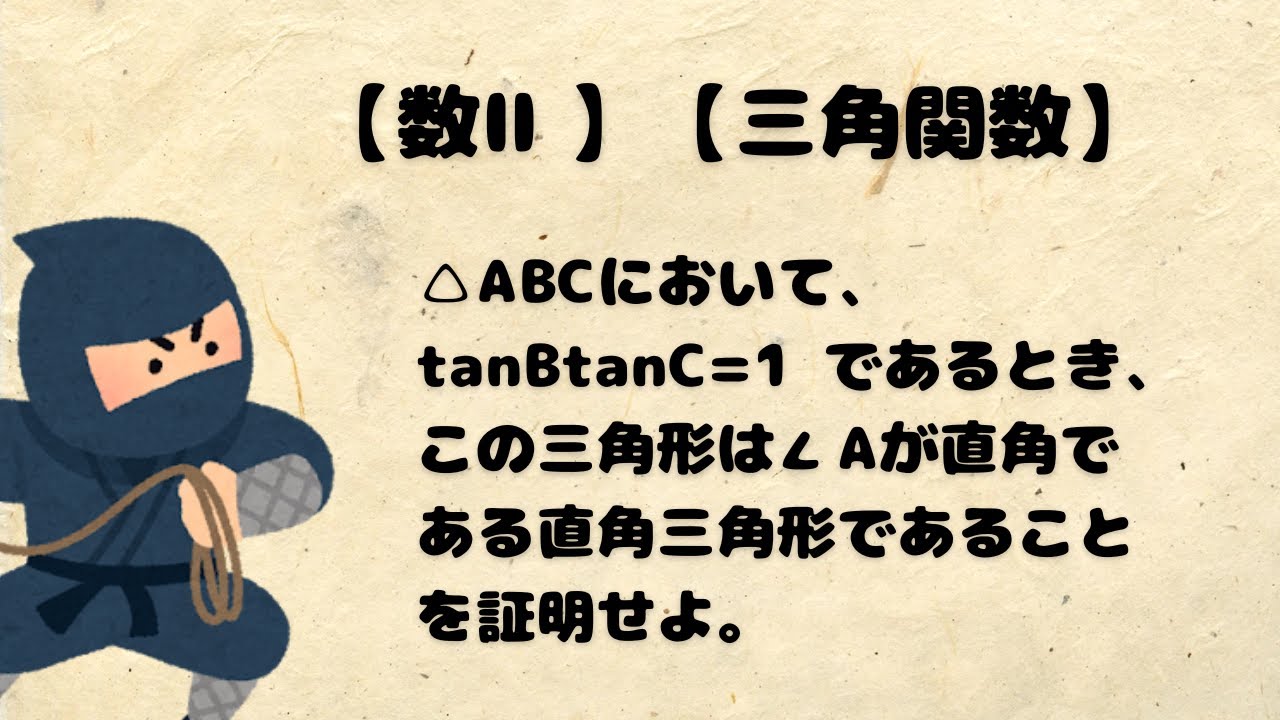
問題文全文(内容文):
$AB = 1, \angle ABC = 90°,\angle BCA = 7.5°$である$△ABC$ の辺BC 上に $AD = CD$ と
なるように点Dをとる。このとき、$BD = \boxed{コ}, CD=\boxed{サ}$である。したがって、
$\tan 7.5° =\frac{1}{\boxed{コ}+\boxed{サ}}$
次に、正の実数kに対して、2直線$y=3kx, y = 4kx$のなす角度を$θ$とする。
だし、$0° \lt θ \lt 90°$である。このとき、$\tanθ = \boxed{シ}$である。したがって、$\tanθ$ は
$k =\frac{1}{\boxed{ス}}$ のとき最大値$\frac{1}{\boxed{セ}}$ をとる。また、$k=\frac{1}{\boxed{ス}}$ のとき$\boxed{ソ}$を満たす。
なお、必要ならば
$\sqrt2 = 1.4, \sqrt3=1.7..., \sqrt5=2.2, \sqrt6=2.4...$
を用いてよい。
$\boxed{コ},\boxed{サ}$の解答群
$ⓐ\sqrt2+\sqrt3\ \ \ ⓑ\sqrt2+\sqrt5\ \ \ ⓒ\sqrt2+\sqrt6\ \ \ ⓓ2+\sqrt3$
$ⓔ2+\sqrt5\ \ \ ⓕ2+\sqrt6\ \ \ ⓖ\sqrt3+\sqrt5\ \ \ ⓗ\sqrt5+\sqrt6$
$\boxed{シ}$の解答群
$ⓐ\frac{k}{1-12k^2}\ \ \ ⓑ\frac{k}{1+12k^2}\ \ \ ⓒ\frac{7k}{1-12k^2}\ \ \ ⓓ\frac{7k}{1+12k^2}$
$ⓔ\frac{12k^2}{1-12k^2}\ \ \ ⓕ\frac{12k^2}{1+12k^2}$
$ⓖ\frac{12k^2}{1-7k^2}\ \ \ ⓗ\frac{12k^2}{1+7k^2}$
$\boxed{ス},\boxed{セ}$の解答群
$ⓐ2\ \ \ ⓑ2\sqrt2\ \ \ ⓒ3\ \ \ ⓓ2\sqrt3\ \ \ ⓔ4\ \ \ ⓕ3\sqrt2$
$ⓖ3\sqrt3 \ \ \ ⓗ4\sqrt2 \ \ \ ⓘ6\ \ \ ⓙ4\sqrt3 \ \ \ ⓚ7\ \ \ ⓛ7\sqrt2$
$\boxed{ソ}$の解答群
$ⓐθ \gt 7.5°\ \ \ ⓑθ = 7.5°\ \ \ ⓒθ \lt 7.5°$
2022中央大学理工学部過去問
$AB = 1, \angle ABC = 90°,\angle BCA = 7.5°$である$△ABC$ の辺BC 上に $AD = CD$ と
なるように点Dをとる。このとき、$BD = \boxed{コ}, CD=\boxed{サ}$である。したがって、
$\tan 7.5° =\frac{1}{\boxed{コ}+\boxed{サ}}$
次に、正の実数kに対して、2直線$y=3kx, y = 4kx$のなす角度を$θ$とする。
だし、$0° \lt θ \lt 90°$である。このとき、$\tanθ = \boxed{シ}$である。したがって、$\tanθ$ は
$k =\frac{1}{\boxed{ス}}$ のとき最大値$\frac{1}{\boxed{セ}}$ をとる。また、$k=\frac{1}{\boxed{ス}}$ のとき$\boxed{ソ}$を満たす。
なお、必要ならば
$\sqrt2 = 1.4, \sqrt3=1.7..., \sqrt5=2.2, \sqrt6=2.4...$
を用いてよい。
$\boxed{コ},\boxed{サ}$の解答群
$ⓐ\sqrt2+\sqrt3\ \ \ ⓑ\sqrt2+\sqrt5\ \ \ ⓒ\sqrt2+\sqrt6\ \ \ ⓓ2+\sqrt3$
$ⓔ2+\sqrt5\ \ \ ⓕ2+\sqrt6\ \ \ ⓖ\sqrt3+\sqrt5\ \ \ ⓗ\sqrt5+\sqrt6$
$\boxed{シ}$の解答群
$ⓐ\frac{k}{1-12k^2}\ \ \ ⓑ\frac{k}{1+12k^2}\ \ \ ⓒ\frac{7k}{1-12k^2}\ \ \ ⓓ\frac{7k}{1+12k^2}$
$ⓔ\frac{12k^2}{1-12k^2}\ \ \ ⓕ\frac{12k^2}{1+12k^2}$
$ⓖ\frac{12k^2}{1-7k^2}\ \ \ ⓗ\frac{12k^2}{1+7k^2}$
$\boxed{ス},\boxed{セ}$の解答群
$ⓐ2\ \ \ ⓑ2\sqrt2\ \ \ ⓒ3\ \ \ ⓓ2\sqrt3\ \ \ ⓔ4\ \ \ ⓕ3\sqrt2$
$ⓖ3\sqrt3 \ \ \ ⓗ4\sqrt2 \ \ \ ⓘ6\ \ \ ⓙ4\sqrt3 \ \ \ ⓚ7\ \ \ ⓛ7\sqrt2$
$\boxed{ソ}$の解答群
$ⓐθ \gt 7.5°\ \ \ ⓑθ = 7.5°\ \ \ ⓒθ \lt 7.5°$
2022中央大学理工学部過去問
単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$AB = 1, \angle ABC = 90°,\angle BCA = 7.5°$である$△ABC$ の辺BC 上に $AD = CD$ と
なるように点Dをとる。このとき、$BD = \boxed{コ}, CD=\boxed{サ}$である。したがって、
$\tan 7.5° =\frac{1}{\boxed{コ}+\boxed{サ}}$
次に、正の実数kに対して、2直線$y=3kx, y = 4kx$のなす角度を$θ$とする。
だし、$0° \lt θ \lt 90°$である。このとき、$\tanθ = \boxed{シ}$である。したがって、$\tanθ$ は
$k =\frac{1}{\boxed{ス}}$ のとき最大値$\frac{1}{\boxed{セ}}$ をとる。また、$k=\frac{1}{\boxed{ス}}$ のとき$\boxed{ソ}$を満たす。
なお、必要ならば
$\sqrt2 = 1.4, \sqrt3=1.7..., \sqrt5=2.2, \sqrt6=2.4...$
を用いてよい。
$\boxed{コ},\boxed{サ}$の解答群
$ⓐ\sqrt2+\sqrt3\ \ \ ⓑ\sqrt2+\sqrt5\ \ \ ⓒ\sqrt2+\sqrt6\ \ \ ⓓ2+\sqrt3$
$ⓔ2+\sqrt5\ \ \ ⓕ2+\sqrt6\ \ \ ⓖ\sqrt3+\sqrt5\ \ \ ⓗ\sqrt5+\sqrt6$
$\boxed{シ}$の解答群
$ⓐ\frac{k}{1-12k^2}\ \ \ ⓑ\frac{k}{1+12k^2}\ \ \ ⓒ\frac{7k}{1-12k^2}\ \ \ ⓓ\frac{7k}{1+12k^2}$
$ⓔ\frac{12k^2}{1-12k^2}\ \ \ ⓕ\frac{12k^2}{1+12k^2}$
$ⓖ\frac{12k^2}{1-7k^2}\ \ \ ⓗ\frac{12k^2}{1+7k^2}$
$\boxed{ス},\boxed{セ}$の解答群
$ⓐ2\ \ \ ⓑ2\sqrt2\ \ \ ⓒ3\ \ \ ⓓ2\sqrt3\ \ \ ⓔ4\ \ \ ⓕ3\sqrt2$
$ⓖ3\sqrt3 \ \ \ ⓗ4\sqrt2 \ \ \ ⓘ6\ \ \ ⓙ4\sqrt3 \ \ \ ⓚ7\ \ \ ⓛ7\sqrt2$
$\boxed{ソ}$の解答群
$ⓐθ \gt 7.5°\ \ \ ⓑθ = 7.5°\ \ \ ⓒθ \lt 7.5°$
2022中央大学理工学部過去問
$AB = 1, \angle ABC = 90°,\angle BCA = 7.5°$である$△ABC$ の辺BC 上に $AD = CD$ と
なるように点Dをとる。このとき、$BD = \boxed{コ}, CD=\boxed{サ}$である。したがって、
$\tan 7.5° =\frac{1}{\boxed{コ}+\boxed{サ}}$
次に、正の実数kに対して、2直線$y=3kx, y = 4kx$のなす角度を$θ$とする。
だし、$0° \lt θ \lt 90°$である。このとき、$\tanθ = \boxed{シ}$である。したがって、$\tanθ$ は
$k =\frac{1}{\boxed{ス}}$ のとき最大値$\frac{1}{\boxed{セ}}$ をとる。また、$k=\frac{1}{\boxed{ス}}$ のとき$\boxed{ソ}$を満たす。
なお、必要ならば
$\sqrt2 = 1.4, \sqrt3=1.7..., \sqrt5=2.2, \sqrt6=2.4...$
を用いてよい。
$\boxed{コ},\boxed{サ}$の解答群
$ⓐ\sqrt2+\sqrt3\ \ \ ⓑ\sqrt2+\sqrt5\ \ \ ⓒ\sqrt2+\sqrt6\ \ \ ⓓ2+\sqrt3$
$ⓔ2+\sqrt5\ \ \ ⓕ2+\sqrt6\ \ \ ⓖ\sqrt3+\sqrt5\ \ \ ⓗ\sqrt5+\sqrt6$
$\boxed{シ}$の解答群
$ⓐ\frac{k}{1-12k^2}\ \ \ ⓑ\frac{k}{1+12k^2}\ \ \ ⓒ\frac{7k}{1-12k^2}\ \ \ ⓓ\frac{7k}{1+12k^2}$
$ⓔ\frac{12k^2}{1-12k^2}\ \ \ ⓕ\frac{12k^2}{1+12k^2}$
$ⓖ\frac{12k^2}{1-7k^2}\ \ \ ⓗ\frac{12k^2}{1+7k^2}$
$\boxed{ス},\boxed{セ}$の解答群
$ⓐ2\ \ \ ⓑ2\sqrt2\ \ \ ⓒ3\ \ \ ⓓ2\sqrt3\ \ \ ⓔ4\ \ \ ⓕ3\sqrt2$
$ⓖ3\sqrt3 \ \ \ ⓗ4\sqrt2 \ \ \ ⓘ6\ \ \ ⓙ4\sqrt3 \ \ \ ⓚ7\ \ \ ⓛ7\sqrt2$
$\boxed{ソ}$の解答群
$ⓐθ \gt 7.5°\ \ \ ⓑθ = 7.5°\ \ \ ⓒθ \lt 7.5°$
2022中央大学理工学部過去問
投稿日:2022.10.16