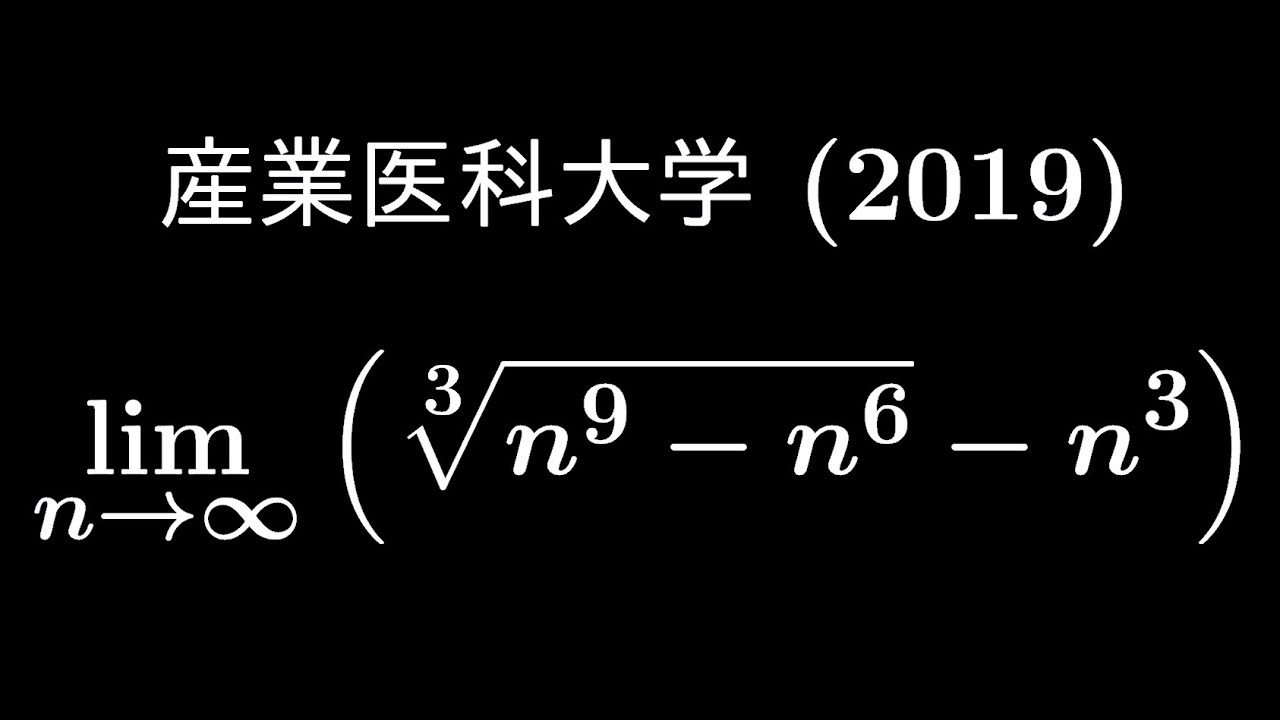問題文全文(内容文):
$\displaystyle \sum_{n=1}^{\infty} \frac{1}{n} $は正の無限大に発散することを用いて、
$\displaystyle \sum_{n=1}^{\infty} \frac{1}{\sqrt n}$が発散することを示せ。
$\displaystyle \sum_{n=1}^{\infty} \frac{1}{n} $は正の無限大に発散することを用いて、
$\displaystyle \sum_{n=1}^{\infty} \frac{1}{\sqrt n}$が発散することを示せ。
チャプター:
00:00 スタート(1)解説
02:11 (2)解説
03:54 エンディング
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#極限
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\displaystyle \sum_{n=1}^{\infty} \frac{1}{n} $は正の無限大に発散することを用いて、
$\displaystyle \sum_{n=1}^{\infty} \frac{1}{\sqrt n}$が発散することを示せ。
$\displaystyle \sum_{n=1}^{\infty} \frac{1}{n} $は正の無限大に発散することを用いて、
$\displaystyle \sum_{n=1}^{\infty} \frac{1}{\sqrt n}$が発散することを示せ。
投稿日:2026.01.24