 中高教材
中高教材
 中高教材
中高教材
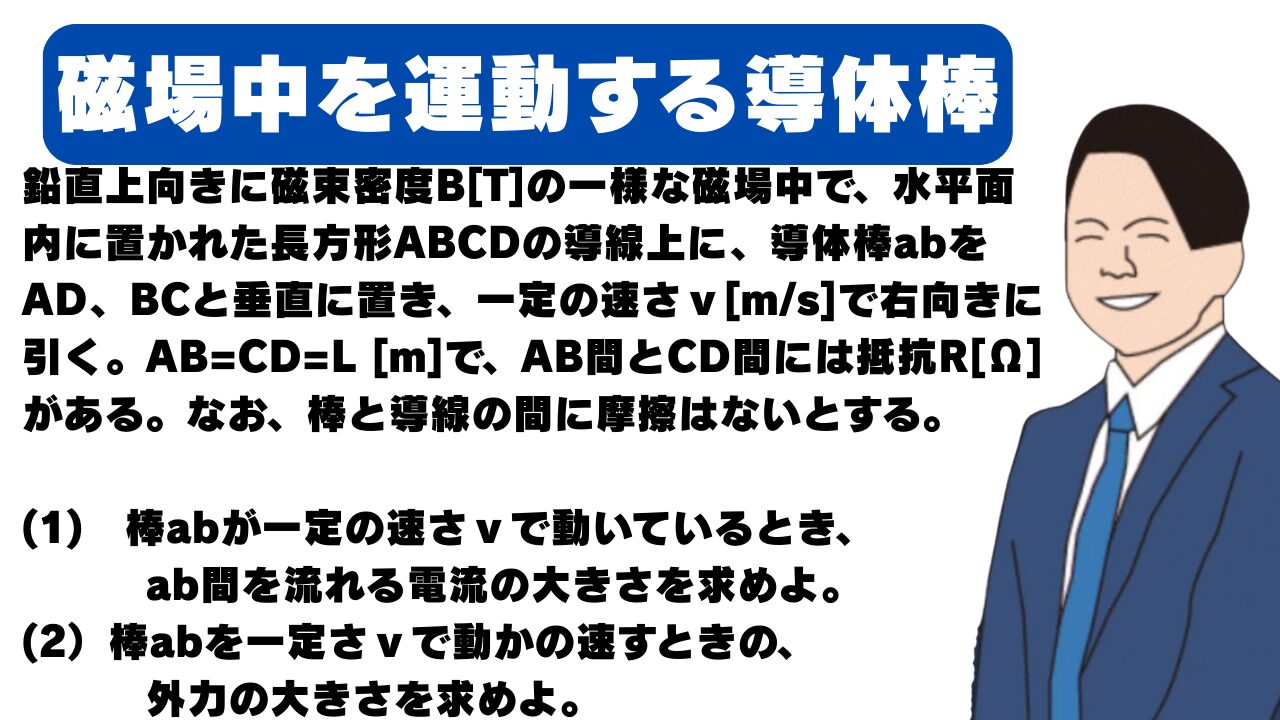
【高校物理】磁場中を運動する導体棒:鉛直上向きに磁束密度B[T]の一様な磁場中で、水平面内に置かれた長方形ABCDの導線上に、導体棒abをAD、BCと垂直に置き、一定の速さv[m/s]で右向きに引く…
単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
鉛直上向きに磁束密度B[T]の一様な磁場中で、水平面内に置かれた長方形ABCDの導線上に、導体棒abをAD、BCと垂直に置き、一定の速さv[m/s]で右向きに引く。AB=CD=L [m]で、AB間とCD間には抵抗R[Ω]がある。なお、棒と導線の間に摩擦はないとする。
(1) 棒abが一定の速さvで動いているとき、ab間を流れる電流の大きさを求めよ。
(2)棒abを一定さvで動かの速すときの、外力の大きさを求めよ。
この動画を見る
鉛直上向きに磁束密度B[T]の一様な磁場中で、水平面内に置かれた長方形ABCDの導線上に、導体棒abをAD、BCと垂直に置き、一定の速さv[m/s]で右向きに引く。AB=CD=L [m]で、AB間とCD間には抵抗R[Ω]がある。なお、棒と導線の間に摩擦はないとする。
(1) 棒abが一定の速さvで動いているとき、ab間を流れる電流の大きさを求めよ。
(2)棒abを一定さvで動かの速すときの、外力の大きさを求めよ。
【高校化学】(1)(ア)~(オ)の各原子の名称を記せ。(2)(ウ)の原子の最外殻には、あと最大何個の電子を収容することができるか。(3)₈Oおよび₁₇Cl原子について、その電子配置を図にならって示せ。

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の電子配置をもつ原子について、下の各問いに答えよ。
(1)(ア)~(オ)の各原子の名称を記せ。また、各原子の価電子の数はいくらか。
(2)(ウ)の原子の最外殻には、あと最大何個の電子を収容することができるか。
(3)₈Oおよび₁₇Cl原子について、その電子配置を図にならって示せ。
この動画を見る
次の電子配置をもつ原子について、下の各問いに答えよ。
(1)(ア)~(オ)の各原子の名称を記せ。また、各原子の価電子の数はいくらか。
(2)(ウ)の原子の最外殻には、あと最大何個の電子を収容することができるか。
(3)₈Oおよび₁₇Cl原子について、その電子配置を図にならって示せ。
【高校物理】平行電流間の力:真空中の同一鉛直面内に、3本の十分に長い導線A、B、Cを平行に張り、図の向きに、I₁=I₂=5.0A、I₃=3.0Aの電流を流す。AC間の距離を2.0m、BC間の距離…

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
真空中の同一鉛直面内に、3本の十分に長い導線A、B、Cを平行に張り、図の向きに、I₁=I₂=5.0A、I₃=3.0Aの電流を流す。AC間の距離を2.0m、BC間の距離を1.0m、真空の透磁率を4π×10⁻⁷N/A²とする。
(1) A、Bの電流が、Cの位置につくる合成磁場の向きと強さを求めよ。
(2) Cの長さ1.0mあたりが、A、Bから受ける力の向きと大きさを求めよ。
この動画を見る
真空中の同一鉛直面内に、3本の十分に長い導線A、B、Cを平行に張り、図の向きに、I₁=I₂=5.0A、I₃=3.0Aの電流を流す。AC間の距離を2.0m、BC間の距離を1.0m、真空の透磁率を4π×10⁻⁷N/A²とする。
(1) A、Bの電流が、Cの位置につくる合成磁場の向きと強さを求めよ。
(2) Cの長さ1.0mあたりが、A、Bから受ける力の向きと大きさを求めよ。
【数Ⅲ】【微分】f'(x)+f(x)=4xe^{-x}sin2x, f(0)=0を満たすとする(1) g(x)=e^xf(x)とおくとg'(x)=4xsin2xとなることを示せ(2) f(x)を求めよ

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
f(x) は微分可能な関数で $f'(x) + f(x) = 4xe^{-x} \sin 2x$,$f(0) = 0$ を満たすとする。
(1)$g(x) = e^x f(x)$とおくと、$g'(x) = 4x \sin 2x$ となることを示せ。
(2) f(x)を求めよ。
この動画を見る
f(x) は微分可能な関数で $f'(x) + f(x) = 4xe^{-x} \sin 2x$,$f(0) = 0$ を満たすとする。
(1)$g(x) = e^x f(x)$とおくと、$g'(x) = 4x \sin 2x$ となることを示せ。
(2) f(x)を求めよ。
【高校物理】ダイオードの特性:図のような特性をもつダイオードを、(1)、(2)のように、電池、抵抗と接続する。各回路の電池に流れる電流は何mAか。ただし、電池の内部抵抗を無視する。

単元:
#物理#電気#理科(高校生)
教材:
#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のような特性をもつダイオードを、(1)、(2)のように、電池、抵抗と接続する。各回路の電池に流れる電流は何mAか。ただし、電池の内部抵抗を無視する。
この動画を見る
図のような特性をもつダイオードを、(1)、(2)のように、電池、抵抗と接続する。各回路の電池に流れる電流は何mAか。ただし、電池の内部抵抗を無視する。
【高校化学】原子:原子に関する記述のうち、正しいものを選べ①原子の半径は原子様の半径のおよそ100~1000倍である。②原子内の陽子の数と電子の数の和を質量数という。③中性子はすべての原子核に含まれる

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
原子:原子に関する記述のうち、正しいもの2つ選び、番号を記せ。
①原子の半径は原子様の半径のおよそ100~1000倍である。
②原子内の陽子の数と電子の数の和を質量数という。
③中性子はすべての原子核に含まれる。
④原子核中の陽子の数が等しい原子とつしは、同じ元素の原子である。
⑤ 陽子、中性子、電子の質量は、ほぼ等しい。
⑥原子には、天然に同位体が存在しないものもある。
この動画を見る
原子:原子に関する記述のうち、正しいもの2つ選び、番号を記せ。
①原子の半径は原子様の半径のおよそ100~1000倍である。
②原子内の陽子の数と電子の数の和を質量数という。
③中性子はすべての原子核に含まれる。
④原子核中の陽子の数が等しい原子とつしは、同じ元素の原子である。
⑤ 陽子、中性子、電子の質量は、ほぼ等しい。
⑥原子には、天然に同位体が存在しないものもある。
【数Ⅲ】【微分】(1) y'=(2x-1)³ [x=0のときy=1](2) (2-x)y'=1 [x=1のときy=0](3) y'=y²cosx/(sinx+1)² [x=0のときy=1]

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
yはxの関数とする。
次の微分方程式を、[ ]内の初期条件のもとで解け。
(1) $\quad y' = (2x - 1)^3$ [x = 0 のとき y = 1]
(2) $\quad (2 - x)y' = 1$ [x = 1 のとき y = 0]
(3) $\quad y' = \displaystyle \frac{y^2 \cos x}{(\sin x + 1)^2}$ [x = 0 のとき y = 1]
この動画を見る
yはxの関数とする。
次の微分方程式を、[ ]内の初期条件のもとで解け。
(1) $\quad y' = (2x - 1)^3$ [x = 0 のとき y = 1]
(2) $\quad (2 - x)y' = 1$ [x = 1 のとき y = 0]
(3) $\quad y' = \displaystyle \frac{y^2 \cos x}{(\sin x + 1)^2}$ [x = 0 のとき y = 1]
【高校化学】同位体には、原子核が不安定なものがあり、( ア )線を放出して、他の元素の原子に変わる。このような同位体を( イ )という。

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の文を読み、下の各問いに答えよ。
同位体には、原子核が不安定なものがあり、( ア )線を放出して、他の元素の原子に変わる。このような同位体を( イ )という。(ア)線には、( ウ )の原子核の流れであるα線や( エ )の流れであるβ線、高エネルギーの電磁波であるγ線などがある。
(1)文中の( )に適当な語句を入れよ。
(2)原子が(ア)線を放出して他の元素の原子に変わることを何というか。
(3)炭素の同位体¹⁴₆C(質量数14陽子数6)は、β線を放出して他の元素の原子に変化する。このとき生じる他の原子は何か。¹⁴₆C(質量数14陽子数6)と同様に示せ。
(4)ある遺跡から発掘された木片を調べると、¹⁴₆C(質量数14陽子数6)の量がもとの1/8であった。¹⁴₆C(質量数14陽子数6)の半減期を5730年とすると、この木片は何年前まで生存していたと考えられるか。整数値で答えよ。
この動画を見る
次の文を読み、下の各問いに答えよ。
同位体には、原子核が不安定なものがあり、( ア )線を放出して、他の元素の原子に変わる。このような同位体を( イ )という。(ア)線には、( ウ )の原子核の流れであるα線や( エ )の流れであるβ線、高エネルギーの電磁波であるγ線などがある。
(1)文中の( )に適当な語句を入れよ。
(2)原子が(ア)線を放出して他の元素の原子に変わることを何というか。
(3)炭素の同位体¹⁴₆C(質量数14陽子数6)は、β線を放出して他の元素の原子に変化する。このとき生じる他の原子は何か。¹⁴₆C(質量数14陽子数6)と同様に示せ。
(4)ある遺跡から発掘された木片を調べると、¹⁴₆C(質量数14陽子数6)の量がもとの1/8であった。¹⁴₆C(質量数14陽子数6)の半減期を5730年とすると、この木片は何年前まで生存していたと考えられるか。整数値で答えよ。
【高校物理】コイルに流れる誘導電流:図のように、一辺の長さL[m]の正方形コイルabcd(抵抗はR[Ω],辺bcはx軸に平行)を、速さL[m/s]でx軸の正の向きに移動させる。x=2L[m]には、

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、一辺の長さL[m]の正方形コイルabcd(抵抗はR[Ω],辺bcはx軸に平行)を、速さL[m/s]でx軸の正の向きに移動させる。x=2L[m]には、紙面に垂直に表から裏の向きに、磁束密度B「T]の一様な磁場が存在する。コイルの辺abがx=0に達する時刻をt=0とし、コイルの自己誘導は無視できるものとする。
(1)コイルを貫く磁束のΦ[Wb]と時刻t[s]との関係を示すグラフを描け。ただし、紙面を表から裏に向かって貫く磁束を正とする。
(2) コイルに流れる誘導電流I[A]と時刻t[s]との関係を示すグラフを描け。ただし、a→b→c→d→の向きに流れる電流を正とする。
この動画を見る
図のように、一辺の長さL[m]の正方形コイルabcd(抵抗はR[Ω],辺bcはx軸に平行)を、速さL[m/s]でx軸の正の向きに移動させる。x=2L[m]には、紙面に垂直に表から裏の向きに、磁束密度B「T]の一様な磁場が存在する。コイルの辺abがx=0に達する時刻をt=0とし、コイルの自己誘導は無視できるものとする。
(1)コイルを貫く磁束のΦ[Wb]と時刻t[s]との関係を示すグラフを描け。ただし、紙面を表から裏に向かって貫く磁束を正とする。
(2) コイルに流れる誘導電流I[A]と時刻t[s]との関係を示すグラフを描け。ただし、a→b→c→d→の向きに流れる電流を正とする。
【数Ⅲ】【微分】yはxの関数とする。次の微分方程式を解け。(1) dy/dx=y/x(2) xy'+1=y(3) (x-1)dy/dx+(y-1)=0(4) (1-x²)y'+xy=0

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#積分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
yはxの関数とする。次の微分方程式を解け。
$\frac{dy}{dx} = \frac{y}{x}$
$xy'+ 1 = y$
$(x - 1)\frac{dy}{dx} + (y - 1) = 0$
$(1 - x^2)y' + xy = 0$
この動画を見る
yはxの関数とする。次の微分方程式を解け。
$\frac{dy}{dx} = \frac{y}{x}$
$xy'+ 1 = y$
$(x - 1)\frac{dy}{dx} + (y - 1) = 0$
$(1 - x^2)y' + xy = 0$
【高校物理】磁場中の荷電粒子の運動:紙面に垂直な磁束密度B[T]の一様な磁場中に、q[C]の正電荷をもつ質量m[kg]の荷電粒子を、磁場と垂直に速さ [m/s] で点Pから入射させた。図のように、粒…

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
紙面に垂直な磁束密度B[T]の一様な磁場中に、q[C]の正電荷をもつ質量m[kg]の荷電粒子を、磁場と垂直に速さ [m/s] で点Pから入射させた。図のように、粒子は、時計まわりに半円の軌道を描いた。
(1)磁場の向きは、図のア、イのどちらか。
(2)荷電粒子が磁場から受ける力の大きさはいくらか。
(3)PQ間の距離はいくらか。
(4)PからQに達するまでの時間はいくらか。
(5)荷電粒子を入射させる速さを2倍にすると、PQ間の距離、PからQに達するまでの時間は、それぞれ(3)、(4)の何倍となるか。
この動画を見る
紙面に垂直な磁束密度B[T]の一様な磁場中に、q[C]の正電荷をもつ質量m[kg]の荷電粒子を、磁場と垂直に速さ [m/s] で点Pから入射させた。図のように、粒子は、時計まわりに半円の軌道を描いた。
(1)磁場の向きは、図のア、イのどちらか。
(2)荷電粒子が磁場から受ける力の大きさはいくらか。
(3)PQ間の距離はいくらか。
(4)PからQに達するまでの時間はいくらか。
(5)荷電粒子を入射させる速さを2倍にすると、PQ間の距離、PからQに達するまでの時間は、それぞれ(3)、(4)の何倍となるか。
【数Ⅲ】【微分】yはxの関数とする。次の微分方程式を解け。kは0でない定数とする。(1) dy/dx=2x+1(2) dy/dx=coskx(3) dy/dx=2/x(4) dy/dx=e^{kx}

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
$y$は$x$の関数とする。次の微分方程式を解け。
ただし$k$は$0$でない定数とする。
(1) $\dfrac{dy}{dx}=2x+1$ (2) $\dfrac{dy}{dx}=\cos kx$
(3) $\dfrac{dy}{dx}=\dfrac2x$ (4) $\dfrac{dy}{dx}=e^{kx}$
この動画を見る
$y$は$x$の関数とする。次の微分方程式を解け。
ただし$k$は$0$でない定数とする。
(1) $\dfrac{dy}{dx}=2x+1$ (2) $\dfrac{dy}{dx}=\cos kx$
(3) $\dfrac{dy}{dx}=\dfrac2x$ (4) $\dfrac{dy}{dx}=e^{kx}$
【高校物理】ソレノイドを流れる電流がつくる磁場:長さ0.20mの中空の円筒に、一様に1.0×10回巻いたソレノイドがある。このソレノイドに0.40Aの電流を流したとき、ソレノイド内部の磁場の強さと、…

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
長さ0.20mの中空の円筒に、一様に1.0×10回巻いたソレノイドがある。このソレノイドに0.40Aの電流を流したとき、ソレノイド内部の磁場の強さと、磁束密度の大きさをそれぞれ求めよ。ただし、空気の透磁率を1.3×10⁻⁶N/A² とする。
この動画を見る
長さ0.20mの中空の円筒に、一様に1.0×10回巻いたソレノイドがある。このソレノイドに0.40Aの電流を流したとき、ソレノイド内部の磁場の強さと、磁束密度の大きさをそれぞれ求めよ。ただし、空気の透磁率を1.3×10⁻⁶N/A² とする。
【数Ⅲ】【微分】f(b)-f(a)/b-a=f'(c),a<c<bにおいてb-a=h,c-a/b-a=θとおくと f(a+h)=f(a)+hf'(a+θh),0<θ<1 と表されることを示せ

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$f(x)$は閉区間$[a,b]$で連続で、開区間$(a,b)$で微分可能であるとする。
平均値の定理の式
$\dfrac{f(b)-f(a)}{b-a}=f'(c),a< c< b$
において
$b-a=h, \dfrac{c-a}{b-a}=\theta$とおくと
$f(a+h)=f(a)+hf'(a+\theta h),0 < \theta < 1$
と表されることを示せ。
この動画を見る
関数$f(x)$は閉区間$[a,b]$で連続で、開区間$(a,b)$で微分可能であるとする。
平均値の定理の式
$\dfrac{f(b)-f(a)}{b-a}=f'(c),a< c< b$
において
$b-a=h, \dfrac{c-a}{b-a}=\theta$とおくと
$f(a+h)=f(a)+hf'(a+\theta h),0 < \theta < 1$
と表されることを示せ。
【高校化学】¹⁶₈O(質量数16陽子数8)、¹⁷₈O(質量数17陽子数8)、¹⁸₈O(質量数18陽子数8)について、陽子の数、中性子の数、電子の数をそれぞれ求めよ。

単元:
#化学#化学基礎1ー物質の構成#原子の構成と元素の周期表#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
天然の酸素原子には¹⁶₈O(質量数16陽子数8)、¹⁷₈O(質量数17陽子数8)、¹⁸₈O(質量数18陽子数8)がある。次の各問いに答えよ。
(1)これらの原子の関係を何というか。
(2)¹⁶₈O(質量数16陽子数8)、¹⁷₈O(質量数17陽子数8)、¹⁸₈O(質量数18陽子数8)について、陽子の数、中性子の数、電子の数をそれぞれ求めよ。
(3)これらの3種類の酸素原子を組み合わせると、何種類の酸素分子O₂ができるか。
この動画を見る
天然の酸素原子には¹⁶₈O(質量数16陽子数8)、¹⁷₈O(質量数17陽子数8)、¹⁸₈O(質量数18陽子数8)がある。次の各問いに答えよ。
(1)これらの原子の関係を何というか。
(2)¹⁶₈O(質量数16陽子数8)、¹⁷₈O(質量数17陽子数8)、¹⁸₈O(質量数18陽子数8)について、陽子の数、中性子の数、電子の数をそれぞれ求めよ。
(3)これらの3種類の酸素原子を組み合わせると、何種類の酸素分子O₂ができるか。
【高校物理】キルヒホッフの法則:図のように、内部抵抗の無視できる起電力がそれぞれ6.4V、 2.0Vの電池E₁、E₂、および抵抗値がそれぞれ5.0Ω、2.0Ω、4.0Ωの抵 抗 R₁、R₂、R₃を…

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、内部抵抗の無視できる起電力がそれぞれ6.4V、 2.0Vの電池E₁、E₂、および抵抗値がそれぞれ5.0Ω、2.0Ω、4.0Ωの抵 抗 R₁、R₂、R₃を接続した。このとき、各抵抗を流れる電流の向きと大きさはいくらか。
この動画を見る
図のように、内部抵抗の無視できる起電力がそれぞれ6.4V、 2.0Vの電池E₁、E₂、および抵抗値がそれぞれ5.0Ω、2.0Ω、4.0Ωの抵 抗 R₁、R₂、R₃を接続した。このとき、各抵抗を流れる電流の向きと大きさはいくらか。
【高校化学】粒子の振動や直進などの運動を(ア)という。固体、液体、気体のいずれの状態でも構成粒子は(ア)をしており、(ア)の激しさは(イ)の状態が最も激しい(ア)によって空間に拡がっていく現象を(ウ)

単元:
#化学#化学基礎1ー物質の構成#物質の成分と構成元素#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の文中の( )に適当な語句、記号を入れよ。
粒子の振動や直進などの運動を( ア )という。固体、液体、気体のいずれの状態でも構成粒子は(ア)をしており、(ア)の激しさは( イ )の状態が最も激しい。構成粒子が、(ア)によって空間に拡がっていく現象を( ウ )という。
この動画を見る
次の文中の( )に適当な語句、記号を入れよ。
粒子の振動や直進などの運動を( ア )という。固体、液体、気体のいずれの状態でも構成粒子は(ア)をしており、(ア)の激しさは( イ )の状態が最も激しい。構成粒子が、(ア)によって空間に拡がっていく現象を( ウ )という。
【高校物理】電流と電子の速さ:断面積2.0×10-⁶m²のアルミニウムの導線に、4.8Aの電流が流れている。アルミニウム1m³ あたりの自由電子の数を6.0×10²³個、電子の電荷を…

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
断面積2.0×10-⁶m²のアルミニウムの導線に、4.8Aの電流が流れている。
アルミニウム1m³ あたりの自由電子の数を6.0×10²³個、電子の電荷を -1.6×10⁻¹⁹Cとして、次の各問に答えよ。
(1) 導線の断面を1s間に通過する電子の数はいくらか。
(2) 電子が移動する平均の速さはいくらか。
この動画を見る
断面積2.0×10-⁶m²のアルミニウムの導線に、4.8Aの電流が流れている。
アルミニウム1m³ あたりの自由電子の数を6.0×10²³個、電子の電荷を -1.6×10⁻¹⁹Cとして、次の各問に答えよ。
(1) 導線の断面を1s間に通過する電子の数はいくらか。
(2) 電子が移動する平均の速さはいくらか。
【高校化学】次の各記述の下線部と状態変化の名称の組み合わせで、正しいものをすべて選べ。(ア)池にはった氷が、昼にはなくなっていた。 昇華(イ)戸外に干しておいた洗濯物が乾いた。 蒸発 (他)

単元:
#化学#化学基礎1ー物質の構成#物質の成分と構成元素#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の各記述の下線部と状態変化の名称の組み合わせで、正しいものをすべて選べ。
(ア)池にはった氷が、昼にはなくなっていた。 昇華
(イ)戸外に干しておいた洗濯物が乾いた。 蒸発
(ウ)アイスクリームの箱の中に入れておいたドライアイスがなくなった。 融解
(エ)熱いお茶を飲もうとしたら、眼鏡が曇った。 凝縮
(オ)冷凍庫の製氷皿に水でぬれた指で触れると、指がくっついた。 凝固
この動画を見る
次の各記述の下線部と状態変化の名称の組み合わせで、正しいものをすべて選べ。
(ア)池にはった氷が、昼にはなくなっていた。 昇華
(イ)戸外に干しておいた洗濯物が乾いた。 蒸発
(ウ)アイスクリームの箱の中に入れておいたドライアイスがなくなった。 融解
(エ)熱いお茶を飲もうとしたら、眼鏡が曇った。 凝縮
(オ)冷凍庫の製氷皿に水でぬれた指で触れると、指がくっついた。 凝固
【数Ⅲ】【微分】 f(x+y)=f(x)f(y)-sinxsiny,f'(0)=0 のとき次を示せ。 (1)f(0)=1 (2)f'(x)=-sinx (3)-1≦f(x+1)-f(x)≦1

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
微分可能な関数f(x)とすべての実数x,yについて次の等式が成り立っている。
f(x+y)=f(x)f(y)-sinxsiny,f'(0)=0
このとき、次のことが成り立つことを示せ。
(1)f(0)=1 (2)f'(x)=-sinx (3)-1≦f(x+1)-f(x)≦1
この動画を見る
微分可能な関数f(x)とすべての実数x,yについて次の等式が成り立っている。
f(x+y)=f(x)f(y)-sinxsiny,f'(0)=0
このとき、次のことが成り立つことを示せ。
(1)f(0)=1 (2)f'(x)=-sinx (3)-1≦f(x+1)-f(x)≦1
【高校物理】電気量の変化:図のように、極板の間隔がdで、電気 容量が3×10⁻⁸Fの平行板コンデンサーに、10Vの電池を接続する。次の各問に答えよ。(1) コンデンサーにたくわえられる電荷はいくらか…

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように、極板の間隔がdで、電気 容量が3×10⁻⁸Fの平行板コンデンサーに、10Vの電池を接続する。次の各問に答えよ。
(1) コンデンサーにたくわえられる電荷はいくらか。
(2) 電池を接続したまま極板の間隔を3dに広げた。このとき、検流計を何Cの正電荷がどちら向きに移動するか。
向きは図のa、bの記号を用いて答えよ。
この動画を見る
図のように、極板の間隔がdで、電気 容量が3×10⁻⁸Fの平行板コンデンサーに、10Vの電池を接続する。次の各問に答えよ。
(1) コンデンサーにたくわえられる電荷はいくらか。
(2) 電池を接続したまま極板の間隔を3dに広げた。このとき、検流計を何Cの正電荷がどちら向きに移動するか。
向きは図のa、bの記号を用いて答えよ。
【数Ⅲ】【関数】f(x)={0 (-1≦x≦1),|x|-1(x<-1,1<x), g(x)={x²-1(x<0), x-1(0≦x)で(gof)(x),(fog)(x)を求めよ。

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\begin{eqnarray}
f(x)
=
\begin{cases}
0 & ( -1 \leqq x \leqq 1 ) \\
|x|-1 & ( x < -1, 1 < x )
\end{cases}
\end{eqnarray}$
$\begin{eqnarray} g(x)
=
\begin{cases}
x^2-1 & ( x < 0 ) \\
x-1 & ( 0\leqq x )
\end{cases}
\end{eqnarray}$
であるとき、
$(g\circ f)(-3),(f\circ g)(-3),(g\circ f)(x),(f\circ g)(x)$
を求めよ。
この動画を見る
$\begin{eqnarray}
f(x)
=
\begin{cases}
0 & ( -1 \leqq x \leqq 1 ) \\
|x|-1 & ( x < -1, 1 < x )
\end{cases}
\end{eqnarray}$
$\begin{eqnarray} g(x)
=
\begin{cases}
x^2-1 & ( x < 0 ) \\
x-1 & ( 0\leqq x )
\end{cases}
\end{eqnarray}$
であるとき、
$(g\circ f)(-3),(f\circ g)(-3),(g\circ f)(x),(f\circ g)(x)$
を求めよ。
【高校物理】電場と仕事:図は、正負等量の2つの点電荷がつくる電場の様子を、10V間隔の等電位線で表したものである。点Dの電位を0Vとし、電荷qを2.0Cの正の電気量をもつ点電荷とする。次の各問に答え…

単元:
#物理#電気#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
図は、正負等量の2つの点電荷がつくる電場の様子を、10V間隔の等電位線で表したものである。
点Dの電位を0Vとし、電荷qを2.0Cの正の電気量をもつ点電荷とする。次の各問に答えよ。
(1)点Bにおける電荷qの静電気力による位置エネルギーはいくらか。
(2)電荷qをA→B→C→Dの順にゆっくりと運ぶとき、外力が正の仕事をする区間はどれか。また、その仕事は何Jか。
(3)電場が電荷qに正の仕事をする区間はどれか。また、その仕事は何Jか。
(4)点D付近は、一様な電場とみなせる。電荷qを点Dに置いたとき、電荷qにはたらく静電気力の大きさと向きを求めよ。
この動画を見る
図は、正負等量の2つの点電荷がつくる電場の様子を、10V間隔の等電位線で表したものである。
点Dの電位を0Vとし、電荷qを2.0Cの正の電気量をもつ点電荷とする。次の各問に答えよ。
(1)点Bにおける電荷qの静電気力による位置エネルギーはいくらか。
(2)電荷qをA→B→C→Dの順にゆっくりと運ぶとき、外力が正の仕事をする区間はどれか。また、その仕事は何Jか。
(3)電場が電荷qに正の仕事をする区間はどれか。また、その仕事は何Jか。
(4)点D付近は、一様な電場とみなせる。電荷qを点Dに置いたとき、電荷qにはたらく静電気力の大きさと向きを求めよ。
【英語】私立一貫校向け英語教材Lesson8--1 Stage3の英文解説

単元:
#英語(高校生)#英文法#否定表現・特別な表現
教材:
#NT ENGLISH SERIES#中高教材#Third Edition Stage3#Lesson8
指導講師:
理数個別チャンネル
問題文全文(内容文):
Tell me what you learned from this book.
I have no idea (as to) why the ancient city disappeared completely.
Why the city disappeared is a mystery, so experts are continuing their research.
The question is who ruled this city two thousand years ago.
What do you think the experts will do with the dinosaur fossils?
I think they will preserve them in a museum.
Who do you suppose is appropriate for the leader of our project?
I suppose Michael is.
この動画を見る
Tell me what you learned from this book.
I have no idea (as to) why the ancient city disappeared completely.
Why the city disappeared is a mystery, so experts are continuing their research.
The question is who ruled this city two thousand years ago.
What do you think the experts will do with the dinosaur fossils?
I think they will preserve them in a museum.
Who do you suppose is appropriate for the leader of our project?
I suppose Michael is.
【高校化学】(1)①~⑥の状態変化の名称をそれぞれ記せ。(2)⑤、⑥の状態変化をしやすい物質の物質名を1つ記せ。(3)同じ質量、同じ圧力下にある固体・液体・気体のうち、密度が最も小さい状態はどれか。

単元:
#化学#化学基礎1ー物質の構成#物質の成分と構成元素#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
図は、物質の三態と三態間の変化を示したものである。次の各問いに答えよ。
(1)①~⑥の状態変化の名称をそれぞれ記せ。
(2)⑤、⑥の状態変化をしやすい物質の物質名を1つ記せ。
(3)同じ質量、同じ圧力下にある固体・液体・気体のうち、密度が最も小さい状態はどれか。
この動画を見る
図は、物質の三態と三態間の変化を示したものである。次の各問いに答えよ。
(1)①~⑥の状態変化の名称をそれぞれ記せ。
(2)⑤、⑥の状態変化をしやすい物質の物質名を1つ記せ。
(3)同じ質量、同じ圧力下にある固体・液体・気体のうち、密度が最も小さい状態はどれか。
【高校化学】化合物Xに含まれる元素をそれぞれ下から選べ(a)ある化合物Xの水溶液の炎色反応を調べると、黄緑色を呈した。次に、この水溶液に硝酸銀水溶液を加えると、白色沈殿を生じた。

単元:
#化学#化学基礎1ー物質の構成#物質の成分と構成元素#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の(a)、(b)の文を読み、化合物X及びYに含まれる元素をそれぞれ下から選べ。
(a)ある化合物Xの水溶液の炎色反応を調べると、黄緑色を呈した。次に、この水溶液に硝酸銀水溶液を加えると、白色沈殿を生じた。
(b)ある化合物Yを加熱すると、無色の気体と無色の液体を生じ、白色の固体が残った。気体は石灰水を白濁し、液体は青色の塩化コバルト紙を赤変させた。また、白色の固体を水に溶かし、炎色反応を調べると、黄色を呈した。
(元素)H C Na S Cl K Ca Ba
この動画を見る
次の(a)、(b)の文を読み、化合物X及びYに含まれる元素をそれぞれ下から選べ。
(a)ある化合物Xの水溶液の炎色反応を調べると、黄緑色を呈した。次に、この水溶液に硝酸銀水溶液を加えると、白色沈殿を生じた。
(b)ある化合物Yを加熱すると、無色の気体と無色の液体を生じ、白色の固体が残った。気体は石灰水を白濁し、液体は青色の塩化コバルト紙を赤変させた。また、白色の固体を水に溶かし、炎色反応を調べると、黄色を呈した。
(元素)H C Na S Cl K Ca Ba
【高校化学】次の(ア)~(エ)の各元素の炎色反応の色を下から選び、番号で答えよ。(ア)リチウムLi (イ)カルシウムCa (ウ)カリウムK (エ)銅Cu①黄色 ②青緑色 ③橙赤色 ④赤紫色 ⑤赤色

単元:
#化学#化学基礎1ー物質の構成#物質の成分と構成元素#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の(ア)~(エ)の各元素の炎色反応の色を下から選び、番号で答えよ。
(ア)リチウムLi (イ)カルシウムCa (ウ)カリウムK (エ)銅Cu
①黄色 ②青緑色 ③橙赤色 ④赤紫色 ⑤赤色
この動画を見る
次の(ア)~(エ)の各元素の炎色反応の色を下から選び、番号で答えよ。
(ア)リチウムLi (イ)カルシウムCa (ウ)カリウムK (エ)銅Cu
①黄色 ②青緑色 ③橙赤色 ④赤紫色 ⑤赤色
【数C】【空間ベクトル】次の方程式で表される球面の中心の座標と半径を求めよ。(1)x²+y²+z²+6x-4y-12z+48=0(2)x²+y²+z²-x+y-7=0
単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の方程式で表される球面の中心の座標と半径を求めよ。
(1)x²+y²+z²+6x-4y-12z+48=0
(2)x²+y²+z²-x+y-7=0
この動画を見る
次の方程式で表される球面の中心の座標と半径を求めよ。
(1)x²+y²+z²+6x-4y-12z+48=0
(2)x²+y²+z²-x+y-7=0
【高校物理】気体の状態変化とエネルギー:理想気体をピストンのついたシリンダーに入れ、その圧力pと体積Vを、図のA→B→C→Aの経路に沿って変化させた。A→B、B→C(pVー定)、C→Aの各過程におい…

単元:
#物理#熱・波・音#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
理想気体をピストンのついたシリンダーに入れ、その圧力pと体積Vを、図のA→B→C→Aの経路に沿って変化させた。A→B、B→C(pVー定)、C→Aの各過程において、気体の温度変化ΔT、内部エネルギーの変化ΔU、気体がされる仕事W、気体に入る熱量Qについて、+、-、および0を表に記入せよ。
この動画を見る
理想気体をピストンのついたシリンダーに入れ、その圧力pと体積Vを、図のA→B→C→Aの経路に沿って変化させた。A→B、B→C(pVー定)、C→Aの各過程において、気体の温度変化ΔT、内部エネルギーの変化ΔU、気体がされる仕事W、気体に入る熱量Qについて、+、-、および0を表に記入せよ。
【数C】【空間ベクトル】定点A(0,0,2),B(1,2,1)とxy平面に同点Pがある。このとき、AP+BPの最小値を求めよ。

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#空間ベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
定点A(0,0,2),B(1,2,1)とxy平面に同点Pがある。このとき、AP+BPの最小値を求めよ。
この動画を見る
定点A(0,0,2),B(1,2,1)とxy平面に同点Pがある。このとき、AP+BPの最小値を求めよ。
