 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田のおもしろ数学219〜複雑な指数方程式

単元:
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{27^x+343^x}{63^x+147^x}=\dfrac{37}{21}$を満たす$x$をすべて求めよ。
この動画を見る
$\dfrac{27^x+343^x}{63^x+147^x}=\dfrac{37}{21}$を満たす$x$をすべて求めよ。
福田の数学〜中央大学2024経済学部第1問(3)〜パスワードで無事にログインできる確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
あるWebサイトにログインするには4桁の暗証番号を入力しなければならないが、それを忘れてしまった。覚えているのは、各桁の数は5以上ですべて異なる数であり、末尾の2桁は$78$か$87$のどちらかということだけである。このWebサイトでは暗証番号は3回まで入力することができるが、記憶に当てはまる班員台で手当たり次第に入力して無事にログインできる確率を求めよ。
この動画を見る
あるWebサイトにログインするには4桁の暗証番号を入力しなければならないが、それを忘れてしまった。覚えているのは、各桁の数は5以上ですべて異なる数であり、末尾の2桁は$78$か$87$のどちらかということだけである。このWebサイトでは暗証番号は3回まで入力することができるが、記憶に当てはまる班員台で手当たり次第に入力して無事にログインできる確率を求めよ。
福田のおもしろ数学218〜不動点と合成関数の作る方程式の解

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=x^2+1$のとき、方程式$f(f(x))=x$を満たす$x$をすべて求めよ。
この動画を見る
$f(x)=x^2+1$のとき、方程式$f(f(x))=x$を満たす$x$をすべて求めよ。
福田の数学〜中央大学2024経済学部第1問(2)〜集合の要素の個数

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$1$から$1000$までの整数全体の集合を$U$とする。$U$の部分集合$A,B$をそれぞれ$A=\{x|xは5の倍数\},B=\{x|xは7の倍数\}$とするとき、$\overline A \cap \overline B$の要素の個数$n(\overline A \cap \overline B)$を求めよ。
この動画を見る
$1$から$1000$までの整数全体の集合を$U$とする。$U$の部分集合$A,B$をそれぞれ$A=\{x|xは5の倍数\},B=\{x|xは7の倍数\}$とするとき、$\overline A \cap \overline B$の要素の個数$n(\overline A \cap \overline B)$を求めよ。
福田のおもしろ数学217〜ルートの中の巨大な数の分数を計算しよう

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{\dfrac{1111111088888889}{123456787654321}}$を計算して下さい
この動画を見る
$\sqrt{\dfrac{1111111088888889}{123456787654321}}$を計算して下さい
福田の数学〜中央大学2024経済学部第1問(1)〜絶対値の付いた2次不等式の解

福田のおもしろ数学216〜三角形の中のある角を求める幾何
福田の数学〜筑波大学2024理系第6問〜純虚数となる条件と複素数平面上の点

単元:
#数Ⅱ#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
定数$\alpha$は実数でない複素数とする。以下の問いに答えよ。
(1) $\dfrac{\alpha - | \alpha|}{\alpha + | \alpha|} $は純虚数であることを示せ。
(2) 純虚数$\beta$で$\dfrac{\beta - | \alpha|}{\alpha + | \alpha|}$が純虚数となるものがただ1つ存在することを示せ。
(3) 複素数$z$を$\dfrac{z - | \alpha|}{\alpha + | \alpha|}$が純虚数となるように動かすとき、$|z|$が最小となる$z$を$\alpha$を用いて示せ。
この動画を見る
定数$\alpha$は実数でない複素数とする。以下の問いに答えよ。
(1) $\dfrac{\alpha - | \alpha|}{\alpha + | \alpha|} $は純虚数であることを示せ。
(2) 純虚数$\beta$で$\dfrac{\beta - | \alpha|}{\alpha + | \alpha|}$が純虚数となるものがただ1つ存在することを示せ。
(3) 複素数$z$を$\dfrac{z - | \alpha|}{\alpha + | \alpha|}$が純虚数となるように動かすとき、$|z|$が最小となる$z$を$\alpha$を用いて示せ。
福田のおもしろ数学215〜三平方の定理が成り立つ左辺の二項のどちらか一方は4の倍数である証明

単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の数$x,y$が$x^2+y^2=z^2$を満たすとき、$x$または$y$は$4$の倍数となることを証明してください。
この動画を見る
正の数$x,y$が$x^2+y^2=z^2$を満たすとき、$x$または$y$は$4$の倍数となることを証明してください。
福田の数学〜筑波大学2024理系第5問〜極値をもつかもたないかを考える

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$a$と$b$は実数の定数とする。関数
$f(x)=(1-2x^2)cos2x+2xsin2x+acos^2x+b\displaystyle \int_{0}^{x } tsin2t dt$
について、以下の問いに答えよ。
(1) $a=8 \pi ^2, \ b=-4 \pi$のとき、$0
(2) 次の条件(B)を満たす$a,b$を求めよ。
(B) $0
この動画を見る
$a$と$b$は実数の定数とする。関数
$f(x)=(1-2x^2)cos2x+2xsin2x+acos^2x+b\displaystyle \int_{0}^{x } tsin2t dt$
について、以下の問いに答えよ。
(1) $a=8 \pi ^2, \ b=-4 \pi$のとき、$0
(2) 次の条件(B)を満たす$a,b$を求めよ。
(B) $0
福田のおもしろ数学214〜与えられた方程式の表すグラフが放物線であることの証明

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{x}+\sqrt{y}=1$のグラフは放物線の一部であることを示してください。
この動画を見る
$\sqrt{x}+\sqrt{y}=1$のグラフは放物線の一部であることを示してください。
福田の数学〜筑波大学2024理系第4問〜媒介変数表示で表された曲線のグラフと面積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標平面において、媒介変数表示$x=-t(t-\dfrac32), y=\sin\pi t ~~ (0\leqq t \leqq 1)$で表される曲線を$C$とする。以下の問いに答えよ
(1) 定積分$\displaystyle \int_0^1 t\sin\pi t dt$を求めよ。
(2) 実数$a$に対し、曲線$C$と直線$x=a$の共有点の個数を求めよ。
(3) 曲線$C$と$x$軸で囲まれた図形の面積を求めよ。
この動画を見る
座標平面において、媒介変数表示$x=-t(t-\dfrac32), y=\sin\pi t ~~ (0\leqq t \leqq 1)$で表される曲線を$C$とする。以下の問いに答えよ
(1) 定積分$\displaystyle \int_0^1 t\sin\pi t dt$を求めよ。
(2) 実数$a$に対し、曲線$C$と直線$x=a$の共有点の個数を求めよ。
(3) 曲線$C$と$x$軸で囲まれた図形の面積を求めよ。
福田のおもしろ数学213〜コンビネーション200から100までを割り切る2桁の最大の素数

単元:
#数A#場合の数と確率#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$_{200} \textrm{C}_{100}$を割り切る2桁の最大の素数は?
この動画を見る
$_{200} \textrm{C}_{100}$を割り切る2桁の最大の素数は?
福田の数学〜筑波大学2024理系第3問〜3次関数のグラフと接線

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=x(x+1)(x-1)$とする。座標平面において、曲線$y=f(x)$を$C$とし、曲線$C$上の点$(t,f(t))$における接線を$L$とする。以下の問いに答えよ。
(1) 直線$L$の方程式を$t$を用いて表せ。
(2) $t \neq 0$のとき、直線$L$と曲線$C$の共有点で、点$(t,f(t))$とは異なるものを$(a,f(a))$とする。$a$を$t$を用いて表せ。また$t$が$0$を除いた実数を動くとき、$f'(t)f'(a)$の最小値を求めよ。
(3) 次の条件Aを満たすような実数$t$の範囲を求めよ。
(A) 曲線$C$上の点$(t,f(t))$における接線が直線$L$と直交するような実数$s$が存在する。
この動画を見る
$f(x)=x(x+1)(x-1)$とする。座標平面において、曲線$y=f(x)$を$C$とし、曲線$C$上の点$(t,f(t))$における接線を$L$とする。以下の問いに答えよ。
(1) 直線$L$の方程式を$t$を用いて表せ。
(2) $t \neq 0$のとき、直線$L$と曲線$C$の共有点で、点$(t,f(t))$とは異なるものを$(a,f(a))$とする。$a$を$t$を用いて表せ。また$t$が$0$を除いた実数を動くとき、$f'(t)f'(a)$の最小値を求めよ。
(3) 次の条件Aを満たすような実数$t$の範囲を求めよ。
(A) 曲線$C$上の点$(t,f(t))$における接線が直線$L$と直交するような実数$s$が存在する。
福田のおもしろ数学212〜三角形の内角に関する不等式の証明

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\triangle \mathrm{ABC}$において、$\frac{\sin A+\sin B}{2}\leqq \sin \frac{A+B}{2} \cdots (*)$を証明してください。
この動画を見る
$\triangle \mathrm{ABC}$において、$\frac{\sin A+\sin B}{2}\leqq \sin \frac{A+B}{2} \cdots (*)$を証明してください。
福田の数学〜筑波大学2024理系第2問〜対数不等式が表す領域と面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#微分法と積分法#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学
指導講師:
福田次郎
問題文全文(内容文):
(1)$x\gt 1, y\gt 1$のとき、$\log_{ x } y+\log_{ y } x\geqq 2$を示せ。
(2)座標平面において、連立不等式$x\gt 1, y\gt 1, \log_{ x } y+\log_{ y } x\lt \frac{5}{2}$の表す領域を図示せよ。
(3)(2)の領域の中で$x^2+y^2\lt 12$を満たす部分に境界線を含めた図形を$\mathit{D}$とする。$\mathit{D}$の面積を求めよ。
この動画を見る
(1)$x\gt 1, y\gt 1$のとき、$\log_{ x } y+\log_{ y } x\geqq 2$を示せ。
(2)座標平面において、連立不等式$x\gt 1, y\gt 1, \log_{ x } y+\log_{ y } x\lt \frac{5}{2}$の表す領域を図示せよ。
(3)(2)の領域の中で$x^2+y^2\lt 12$を満たす部分に境界線を含めた図形を$\mathit{D}$とする。$\mathit{D}$の面積を求めよ。
福田のおもしろ数学211〜証明しやすく変形するコツ〜不等式の証明

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$x>0, \, y>0, \, 0 < p < 1$ のとき、$(x+y)^p < x^p+y^p$ が成り立つことを示せ。
この動画を見る
$x>0, \, y>0, \, 0 < p < 1$ のとき、$(x+y)^p < x^p+y^p$ が成り立つことを示せ。
福田の数学〜筑波大学2024理系第1問〜交点の位置ベクトルと面積面積
単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
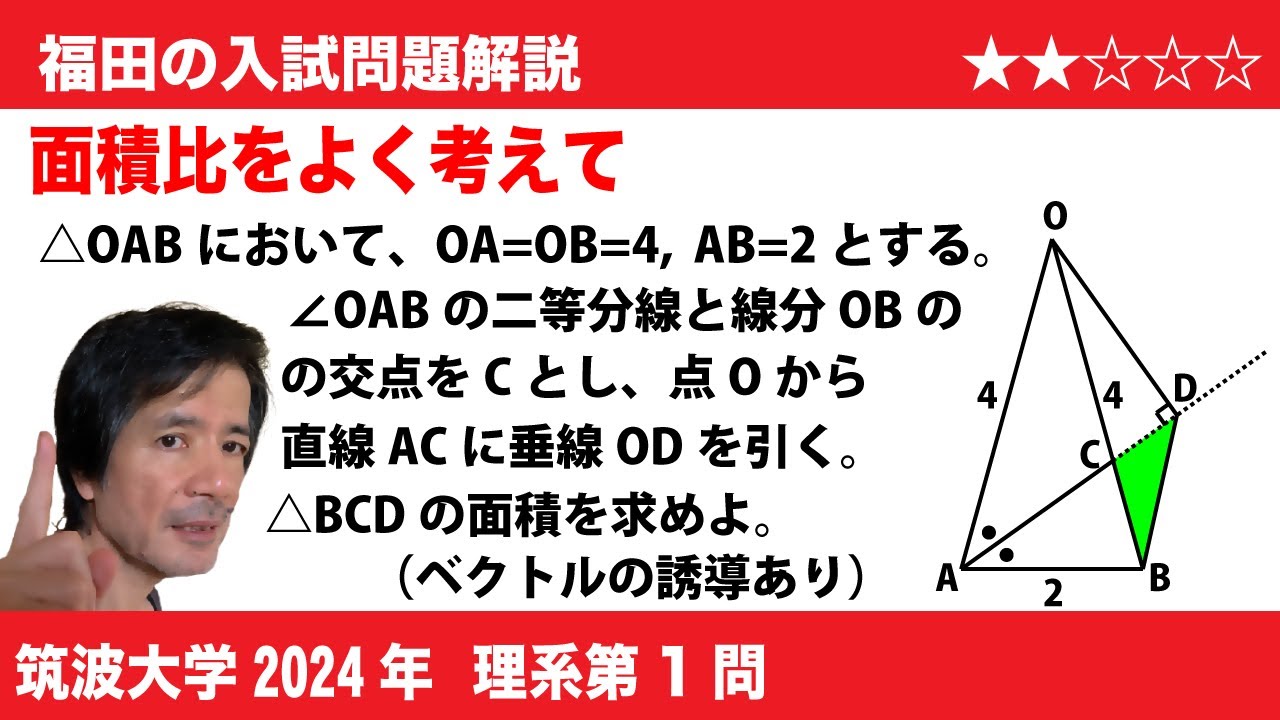
$\triangle \mathrm{OAB}$ において、$\mathrm{OA}=\mathrm{OB}=2$ とする。$\angle \mathrm{OAB}$ の二等分線と線分 $\mathrm{OB}$ の交点を $\mathrm{C}$ とし、点 $\mathrm{O}$ から直線 $\mathrm{AC}$ に垂線 $\mathrm{OD}$ を引く。$\vec{\mathrm{OA}}=\vec{a}, \, \vec{\mathrm{OB}}=\vec{b}$ とおく。以下の問いに答えよ。
$(1)$ $\vec{\mathrm{AC}}$ を $\vec{a}$ と $\vec{b}$ を用いて表せ。
$(2)$ $\vec{\mathrm{OD}}$ を $\vec{a}$ と $\vec{b}$ を用いて表せ。
この動画を見る
$\triangle \mathrm{OAB}$ において、$\mathrm{OA}=\mathrm{OB}=2$ とする。$\angle \mathrm{OAB}$ の二等分線と線分 $\mathrm{OB}$ の交点を $\mathrm{C}$ とし、点 $\mathrm{O}$ から直線 $\mathrm{AC}$ に垂線 $\mathrm{OD}$ を引く。$\vec{\mathrm{OA}}=\vec{a}, \, \vec{\mathrm{OB}}=\vec{b}$ とおく。以下の問いに答えよ。
$(1)$ $\vec{\mathrm{AC}}$ を $\vec{a}$ と $\vec{b}$ を用いて表せ。
$(2)$ $\vec{\mathrm{OD}}$ を $\vec{a}$ と $\vec{b}$ を用いて表せ。
福田のおもしろ数学210〜2つ対称式の条件から和を求める

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#式の計算(整式・展開・因数分解)#数学オリンピック#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
実数 $x, \, y$ が $(1+x)(1+y)(x+y)=2022, \, x^3+y^3=1933$ を満たすとき、$x+y=?$
この動画を見る
実数 $x, \, y$ が $(1+x)(1+y)(x+y)=2022, \, x^3+y^3=1933$ を満たすとき、$x+y=?$
福田の数学〜千葉大学2024年理系第9問〜漸化式と極限

単元:
#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$m$を$0$以上の整数、$n$を$1$以上の整数、$t$を $0 < t < 1$ を満たす実数とし、$F(m, n)$を
$F(m, n)= \displaystyle \sum_{k=m}^{m+n-1} {{}_k \mathrm{ C }_m t^k}$
で定める。
(1) $p$を整数とする。
$
A = \dfrac{(t - 1) F(m + 1, n) + tF(m, n)}{t ^ p}
$
が$t$によらない値となる$p$と、そのときの$A$を求めよ。
(2)極限 $\displaystyle \lim_{ n \to \infty } F(m, n)$ が収束することを示し、その極限値を求めよ。ただし、$0 < s < 1$のとき
$ \displaystyle \lim_{ k \to \infty }k ^ m s ^ k$
であることは用いてよい。
この動画を見る
$m$を$0$以上の整数、$n$を$1$以上の整数、$t$を $0 < t < 1$ を満たす実数とし、$F(m, n)$を
$F(m, n)= \displaystyle \sum_{k=m}^{m+n-1} {{}_k \mathrm{ C }_m t^k}$
で定める。
(1) $p$を整数とする。
$
A = \dfrac{(t - 1) F(m + 1, n) + tF(m, n)}{t ^ p}
$
が$t$によらない値となる$p$と、そのときの$A$を求めよ。
(2)極限 $\displaystyle \lim_{ n \to \infty } F(m, n)$ が収束することを示し、その極限値を求めよ。ただし、$0 < s < 1$のとき
$ \displaystyle \lim_{ k \to \infty }k ^ m s ^ k$
であることは用いてよい。
福田のおもしろ数学209〜無理不等式の解き方

単元:
#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の変化(グラフ・最大最小・方程式・不等式)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt{x}+sqrt{x-2} < 3$を解いて下さい。
この動画を見る
$\sqrt{x}+sqrt{x-2} < 3$を解いて下さい。
福田のおもしろ数学208〜必要条件で絞って十分で切り返す

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=ax^3+bx^2+c$ がある。
すべての整数 $n$ に対して $f(n)$ が整数となるための $a,b,c$ の必要十分条件を求めよ。
この動画を見る
$f(x)=ax^3+bx^2+c$ がある。
すべての整数 $n$ に対して $f(n)$ が整数となるための $a,b,c$ の必要十分条件を求めよ。
福田の数学〜千葉大学2024年理系第7問〜3次方程式の解の極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$n$ を正の整数とする。 $x$ の関数 $f(x) $$= x^3$$-2nx^2$$+(2n-3)x$$+1$ について、以下の問いに答えよ。
$(1)$ $\alpha$ を $f(x)=0$ の$1$ つの解とする。 $\displaystyle f(\frac{1}{1-\alpha})$ の値を求めよ。
$(2)$ 方程式 $f(x) = 0$ は異なる $3$ つの実数解をもつことを示せ。
$(3)$ 方程式 $f(x) = 0$ の解で $2$ 番目に大きいものを $\beta_n$ とする。極限 $\displaystyle \lim_{ n \to \infty } \beta_n$ を求めよ。
この動画を見る
$n$ を正の整数とする。 $x$ の関数 $f(x) $$= x^3$$-2nx^2$$+(2n-3)x$$+1$ について、以下の問いに答えよ。
$(1)$ $\alpha$ を $f(x)=0$ の$1$ つの解とする。 $\displaystyle f(\frac{1}{1-\alpha})$ の値を求めよ。
$(2)$ 方程式 $f(x) = 0$ は異なる $3$ つの実数解をもつことを示せ。
$(3)$ 方程式 $f(x) = 0$ の解で $2$ 番目に大きいものを $\beta_n$ とする。極限 $\displaystyle \lim_{ n \to \infty } \beta_n$ を求めよ。
福田のおもしろ数学207〜不等式の証明と図形的な意味

単元:
#数Ⅱ#微分法と積分法#面積・体積・長さ・速度#面積、体積#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a \geqq b \gt 0,n$ は正の整数とする。
$a^n-b^n \leqq \frac{n}{2}(a-b)(a^{n-1}+b^{n-1})$ であることを証明せよ。
この動画を見る
$a \geqq b \gt 0,n$ は正の整数とする。
$a^n-b^n \leqq \frac{n}{2}(a-b)(a^{n-1}+b^{n-1})$ であることを証明せよ。
福田の数学〜千葉大学2024年理系第6問〜最小値と方程式の解と回転体の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数 $f(x)=e^x+e^{-2x}$ について、次の問いに答えよ。
$(1)$ 関数 $f(x)$ の最小値を求めよ。
$(2)$ $f(x)=2$ となる $x$ の値をすべて求めよ。
$(3)$ $(2)$ で求めた $x$ の値のうち最小のものを $a_1$ 、最大のものを $a_2$ とする。 $y=f(x)$ のグラフ、 $x$ 軸、直線 $x=a_1$、直線 $x=a_2$ で囲まれる図形を $x$ 軸の周りに $1$ 回転してできる立体の体積を求めよ。
この動画を見る
関数 $f(x)=e^x+e^{-2x}$ について、次の問いに答えよ。
$(1)$ 関数 $f(x)$ の最小値を求めよ。
$(2)$ $f(x)=2$ となる $x$ の値をすべて求めよ。
$(3)$ $(2)$ で求めた $x$ の値のうち最小のものを $a_1$ 、最大のものを $a_2$ とする。 $y=f(x)$ のグラフ、 $x$ 軸、直線 $x=a_1$、直線 $x=a_2$ で囲まれる図形を $x$ 軸の周りに $1$ 回転してできる立体の体積を求めよ。
福田の数学〜立教大学2024年経済学部第1問(4)〜三角関数の計算

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \theta = \frac{\pi}{12}$ のとき、$\displaystyle \frac{1}{\tan \theta} - \tan \theta$ の値は $\fbox{キ}$ である。
この動画を見る
$\displaystyle \theta = \frac{\pi}{12}$ のとき、$\displaystyle \frac{1}{\tan \theta} - \tan \theta$ の値は $\fbox{キ}$ である。
福田のおもしろ数学206〜x乗根の方程式の解

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\sqrt[ x ]{ 36 } + \sqrt[ x ]{ 24 } = \sqrt[ x ]{ 16 }$ を満たす $x$ を求めよ。
この動画を見る
$\sqrt[ x ]{ 36 } + \sqrt[ x ]{ 24 } = \sqrt[ x ]{ 16 }$ を満たす $x$ を求めよ。
福田の数学〜千葉大学2024年理系第5問〜確率と極限

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$n$ を $3$ 以上の整数とする。座標平面上の $2n$ 個の点からなる集合
$\{ (x,y) | x=1,2,3, \cdots , n , y=1,2 \}$
を考える。この集合から異なる $3$ 点を無作為に選び、その $3$ 点を線分で結んで得られる図形の面積を $X$ とする。ただし、 $3$ 点が同一直線上にあるときは $X=0$ とする。
$(1)$ $k$ が $0$ 以上の整数のとき、 $X$ が $\displaystyle \frac{k}{2}$ となる確率 $p_k$ を $n$ と $k$ の式で表せ。
$(2)$ $X$ が $\displaystyle \frac{n}{4}$ 以下となる確率を $q_n$ とおく。 $\displaystyle \lim_{n \to \infty} q_n$ を求めよ。
この動画を見る
$n$ を $3$ 以上の整数とする。座標平面上の $2n$ 個の点からなる集合
$\{ (x,y) | x=1,2,3, \cdots , n , y=1,2 \}$
を考える。この集合から異なる $3$ 点を無作為に選び、その $3$ 点を線分で結んで得られる図形の面積を $X$ とする。ただし、 $3$ 点が同一直線上にあるときは $X=0$ とする。
$(1)$ $k$ が $0$ 以上の整数のとき、 $X$ が $\displaystyle \frac{k}{2}$ となる確率 $p_k$ を $n$ と $k$ の式で表せ。
$(2)$ $X$ が $\displaystyle \frac{n}{4}$ 以下となる確率を $q_n$ とおく。 $\displaystyle \lim_{n \to \infty} q_n$ を求めよ。
福田のおもしろ数学205〜不定積分の計算

単元:
#積分とその応用#不定積分#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \int \dfrac{1}{1+\sin x + \cos x}dx$を求めよ。
この動画を見る
$\displaystyle \int \dfrac{1}{1+\sin x + \cos x}dx$を求めよ。
福田の数学〜千葉大学2024年理系第4問(3)〜コンビネーションに関する不等式の評価

単元:
#数A#大学入試過去問(数学)#場合の数#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の整数$n,p,q$が$p > q$かつ$_p\mathrm{C}_2+_q\mathrm{C}_2=n$を満たすとする。$_m\mathrm{C}_2 \leqq n$となる最大の整数$m$を求めよ。
この動画を見る
正の整数$n,p,q$が$p > q$かつ$_p\mathrm{C}_2+_q\mathrm{C}_2=n$を満たすとする。$_m\mathrm{C}_2 \leqq n$となる最大の整数$m$を求めよ。



