 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田の数学〜多変数の方程式はこう扱え〜早稲田大学2023年社会科学部第2問〜3変数の不定方程式の整数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 定数$m$に対して$x$,$y$,$z$の方程式
$xyz$+$x$+$y$+$z$=$xy$+$yz$+$zx$+$m$ ...①
を考える。次の問いに答えよ。
(1)$m$=1のとき①式を満たす実数$x$,$y$,$z$の組を全て求めよ。
(2)$m$=5のとき①式を満たす整数$x$,$y$,$z$の組を全て求めよ。ただし、
$x$≦$y$≦$z$ とする。
(3)$xyz$=$x$+$y$+$z$ を満たす整数$x$,$y$,$z$の組を全て求めよ。ただし、
0<$x$≦$y$≦$z$ とする。
この動画を見る
$\Large{\boxed{2}}$ 定数$m$に対して$x$,$y$,$z$の方程式
$xyz$+$x$+$y$+$z$=$xy$+$yz$+$zx$+$m$ ...①
を考える。次の問いに答えよ。
(1)$m$=1のとき①式を満たす実数$x$,$y$,$z$の組を全て求めよ。
(2)$m$=5のとき①式を満たす整数$x$,$y$,$z$の組を全て求めよ。ただし、
$x$≦$y$≦$z$ とする。
(3)$xyz$=$x$+$y$+$z$ を満たす整数$x$,$y$,$z$の組を全て求めよ。ただし、
0<$x$≦$y$≦$z$ とする。
福田の数学〜接線と放物線で囲まれた面積3連発だ〜早稲田大学2023年社会科学部第1問〜接線と放物線で囲まれた面積

単元:
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ 曲線$y$=$ax^2$+$b$上に$x$座標が$p$である点Pをとり、点Pにおける接線を$l$とする。ただし、定数$a$,$b$は$a$>0, $b$>0とする。次の問いに答えよ。
(1)接線$l$の方程式を$a$,$b$,$p$を用いて表せ。
(2)接線$l$と曲線$y$=$ax^2$で囲まれた図形の面積Sを$a$,$b$を用いて表せ。
(3)接線$l$と曲線$y$=$ax^2$+$\frac{b}{2}$で囲まれた図形の面積をS'としたとき、S'をSを用いて表せ。
(4)接線$l$と曲線$y$=$ax^2$+$c$で囲まれた図形の面積をS''とする。S"=$\frac{S}{2}$のとき、$c$を$a$,$b$を用いて表せ。ただし、$b$>$c$とする。
この動画を見る
$\Large{\boxed{1}}$ 曲線$y$=$ax^2$+$b$上に$x$座標が$p$である点Pをとり、点Pにおける接線を$l$とする。ただし、定数$a$,$b$は$a$>0, $b$>0とする。次の問いに答えよ。
(1)接線$l$の方程式を$a$,$b$,$p$を用いて表せ。
(2)接線$l$と曲線$y$=$ax^2$で囲まれた図形の面積Sを$a$,$b$を用いて表せ。
(3)接線$l$と曲線$y$=$ax^2$+$\frac{b}{2}$で囲まれた図形の面積をS'としたとき、S'をSを用いて表せ。
(4)接線$l$と曲線$y$=$ax^2$+$c$で囲まれた図形の面積をS''とする。S"=$\frac{S}{2}$のとき、$c$を$a$,$b$を用いて表せ。ただし、$b$>$c$とする。
福田の数学〜剰余類と合同式を練習だ〜早稲田大学2023年商学部第3問〜7で割り切れる条件と91で割り切れる条件

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ $n$を正の整数とする。次の設問に答えよ。
(1)$n^2$+$n$+1が7で割り切れるような$n$を小さい順に並べるとき、100番目の整数$n$を求めよ。
(2)$n^2$+$n$+1が91で割り切れるような$n$を小さい順に並べるとき、100番目の整数$n$を求めよ。
この動画を見る
$\Large{\boxed{3}}$ $n$を正の整数とする。次の設問に答えよ。
(1)$n^2$+$n$+1が7で割り切れるような$n$を小さい順に並べるとき、100番目の整数$n$を求めよ。
(2)$n^2$+$n$+1が91で割り切れるような$n$を小さい順に並べるとき、100番目の整数$n$を求めよ。
福田の数学〜どれだけの情報を引き出せるかが勝負〜早稲田大学2023年商学部第2問〜球に内接する四面体の体積の最大

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 中心O、半径1の球に内接する四面体で、その4頂点$T_1$, $T_2$, $T_3$, $T_4$が次の条件(i), (ii)を満たすものを考える。
(i)|$\overrightarrow{T_1T_2}$|=$\sqrt 3$
(ii)$k$($\overrightarrow{OT_1}$+$\overrightarrow{OT_2}$)+$\overrightarrow{OT_3}$+$\overrightarrow{OT_4}$=$\overrightarrow{0}$
ここで、$k$は2未満の正の実数とする。次の設問に答えよ。
(1)線分$T_3T_4$の中点をMとしたとき、$\triangleT_1T_2M$の面積を$k$を用いて表せ。
(2)各$k$に対し、上の条件を満たす四面体の体積の最大値を$V(k)$とする。$V(k)$が最大になるときの$k$の値を求めよ。
この動画を見る
$\Large{\boxed{2}}$ 中心O、半径1の球に内接する四面体で、その4頂点$T_1$, $T_2$, $T_3$, $T_4$が次の条件(i), (ii)を満たすものを考える。
(i)|$\overrightarrow{T_1T_2}$|=$\sqrt 3$
(ii)$k$($\overrightarrow{OT_1}$+$\overrightarrow{OT_2}$)+$\overrightarrow{OT_3}$+$\overrightarrow{OT_4}$=$\overrightarrow{0}$
ここで、$k$は2未満の正の実数とする。次の設問に答えよ。
(1)線分$T_3T_4$の中点をMとしたとき、$\triangleT_1T_2M$の面積を$k$を用いて表せ。
(2)各$k$に対し、上の条件を満たす四面体の体積の最大値を$V(k)$とする。$V(k)$が最大になるときの$k$の値を求めよ。
福田の数学〜早稲田大学2023年商学部第1問(4)〜空間内の格子点から正三角形ができる確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$
(4)次の操作(*)を考える。
(*)1個のさいころを3回続けて投げ、出た目を順に$a_1$, $a_2$, $a_3$とする。
$a_1$, $a_2$, $a_3$を3で割った余りをそれぞれ$r_1$, $r_2$, $r_3$とするとき、座標空間の点($r_1$, $r_2$, $r_3$)を定める。
この操作(*)を3回続けて行い、定まる点を順に$A_1$, $A_2$, $A_3$とする。このとき、$A_1$, $A_2$, $A_3$が正三角形の異なる3頂点となる確率は$\boxed{\ \ エ\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$
(4)次の操作(*)を考える。
(*)1個のさいころを3回続けて投げ、出た目を順に$a_1$, $a_2$, $a_3$とする。
$a_1$, $a_2$, $a_3$を3で割った余りをそれぞれ$r_1$, $r_2$, $r_3$とするとき、座標空間の点($r_1$, $r_2$, $r_3$)を定める。
この操作(*)を3回続けて行い、定まる点を順に$A_1$, $A_2$, $A_3$とする。このとき、$A_1$, $A_2$, $A_3$が正三角形の異なる3頂点となる確率は$\boxed{\ \ エ\ \ }$である。
福田の数学〜早稲田大学2023年商学部第1問(3)〜条件を満たす最小次数の関数を求める

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$
(3)$n$を正の整数とする。次の条件(i),(ii),(iii)を満たす$n$次関数$f(x)$のうち$n$が最小のものは、$f(x)$=$\boxed{\ \ ウ\ \ }$である。
(i) $f(1)$=2
(ii) $\displaystyle\int_{-1}^1(x+1)f(x)dx$=0
(iii) すべての正の整数$m$に対して、$\displaystyle\int_{-1}^1|x|^mf(x)dx$=0
この動画を見る
$\Large{\boxed{1}}$
(3)$n$を正の整数とする。次の条件(i),(ii),(iii)を満たす$n$次関数$f(x)$のうち$n$が最小のものは、$f(x)$=$\boxed{\ \ ウ\ \ }$である。
(i) $f(1)$=2
(ii) $\displaystyle\int_{-1}^1(x+1)f(x)dx$=0
(iii) すべての正の整数$m$に対して、$\displaystyle\int_{-1}^1|x|^mf(x)dx$=0
福田の数学〜早稲田大学2023年商学部第1問(2)〜三角形の内接円の半径と不定方程式

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$m,n$は自然数。半径1の円に内接する$\triangle {ABC}$が
$\sin {\angle A}=\require{physics}\flatfrac{m}{17}$、$\sin {\angle B}=\require{physics}\flatfrac{n}{17}$、
$\sin^2\angle C=\sin^2\angle A+\sin^2\angle B$
を満たすとき、$\triangle {ABC}$の内接円の半径は?
2023早稲田大学商学部過去問
この動画を見る
$m,n$は自然数。半径1の円に内接する$\triangle {ABC}$が
$\sin {\angle A}=\require{physics}\flatfrac{m}{17}$、$\sin {\angle B}=\require{physics}\flatfrac{n}{17}$、
$\sin^2\angle C=\sin^2\angle A+\sin^2\angle B$
を満たすとき、$\triangle {ABC}$の内接円の半径は?
2023早稲田大学商学部過去問
福田の数学〜早稲田大学2023年商学部第1問(1)〜面積計算と不等式の評価

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$
(1)$n$を2以上の整数とする。整数$k$$\in$$\left\{1,2,...,n\right\}$に対し、$y$軸に平行な直線$x$=$2^{k-1}$と曲線$y$=$\log_2 x$の交点を$P_k$とする。このとき、線分$P_1P_2$, $P_2P_3$, ..., $P_{n-1}P_n$と直線$x$=$2^{n-1}$および$x$軸で囲まれる図形の面積を$S(n)$とする。不等式
$\displaystyle\frac{S(n)}{2^n}$≧2023
を満たす最小の$n$は$\boxed{\ \ ア\ \ }$である。
この動画を見る
$\Large{\boxed{1}}$
(1)$n$を2以上の整数とする。整数$k$$\in$$\left\{1,2,...,n\right\}$に対し、$y$軸に平行な直線$x$=$2^{k-1}$と曲線$y$=$\log_2 x$の交点を$P_k$とする。このとき、線分$P_1P_2$, $P_2P_3$, ..., $P_{n-1}P_n$と直線$x$=$2^{n-1}$および$x$軸で囲まれる図形の面積を$S(n)$とする。不等式
$\displaystyle\frac{S(n)}{2^n}$≧2023
を満たす最小の$n$は$\boxed{\ \ ア\ \ }$である。
福田のおもしろ数学~第1回〜どっちがお得〜1年ごとに10万円昇給と半年ごとに3万円昇給
単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
ある社員に2つの昇給プランが提示された。
プランA:年俸は1年に1回支払われ、毎回10万円昇給する。
プランB:年棒は半年に1回支払われ、毎回3万円昇給する。
どちらのプランを選ぶべきか?
この動画を見る
ある社員に2つの昇給プランが提示された。
プランA:年俸は1年に1回支払われ、毎回10万円昇給する。
プランB:年棒は半年に1回支払われ、毎回3万円昇給する。
どちらのプランを選ぶべきか?
福田の数学〜早稲田大学2023年教育学部第4問〜円との最短距離が一定である点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面上の点(0,1)を中心として半径1の円を$C$とする。点P($x$,$y$)が$y$≧0の範囲にあり、PからCまでの最短距離は$ay$であるとする。ただし$a$は0<$a$<1を満たす定数である。このとき、次の問いに答えよ。
(1)点Pが円$C$の円周上または外部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(2)点Pが円$C$の円周上または内部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(3)$x$=$\displaystyle\frac{1}{2}$かつ0≦$y$≦2を満たす点P($x$,$y$)がちょうど3個存在するような定数$a$の範囲を求めよ。
この動画を見る
$\Large\boxed{4}$ 座標平面上の点(0,1)を中心として半径1の円を$C$とする。点P($x$,$y$)が$y$≧0の範囲にあり、PからCまでの最短距離は$ay$であるとする。ただし$a$は0<$a$<1を満たす定数である。このとき、次の問いに答えよ。
(1)点Pが円$C$の円周上または外部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(2)点Pが円$C$の円周上または内部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(3)$x$=$\displaystyle\frac{1}{2}$かつ0≦$y$≦2を満たす点P($x$,$y$)がちょうど3個存在するような定数$a$の範囲を求めよ。
福田の数学〜早稲田大学2023年教育学部第3問〜関数の増減と回転体の体積

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#立体図形#体積・表面積・回転体・水量・変化のグラフ#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 実数$a$,$b$>0に対し、$a$≦$b$の場合は$a$≦$x$≦$b$の範囲、$a$>$b$の場合は$b$≦$x$≦$a$の範囲における$y$=$\log x$のグラフを$C_{a,b}$とする。このとき、次の問いに答えよ。
(1)点(2,-1)と$C_{2,b}$上の点との距離の最小値を$b$を用いて表せ。
(2)直線$x$=$a$と直線$x$=$b$の間で、$C_{a,b}$と$x$軸によって囲まれる部分を$x$軸の周りに1回転して得られる立体の体積を$S_{a,b}$とする。$S_{1,b}$を$b$を用いて表せ。
(3)$S_{a,b}$を(2)で定義したものとする。$S_{a,a+1}$が最小値をとる$a$の値を求めよ。
この動画を見る
$\Large\boxed{3}$ 実数$a$,$b$>0に対し、$a$≦$b$の場合は$a$≦$x$≦$b$の範囲、$a$>$b$の場合は$b$≦$x$≦$a$の範囲における$y$=$\log x$のグラフを$C_{a,b}$とする。このとき、次の問いに答えよ。
(1)点(2,-1)と$C_{2,b}$上の点との距離の最小値を$b$を用いて表せ。
(2)直線$x$=$a$と直線$x$=$b$の間で、$C_{a,b}$と$x$軸によって囲まれる部分を$x$軸の周りに1回転して得られる立体の体積を$S_{a,b}$とする。$S_{1,b}$を$b$を用いて表せ。
(3)$S_{a,b}$を(2)で定義したものとする。$S_{a,a+1}$が最小値をとる$a$の値を求めよ。
福田の数学〜早稲田大学2023年教育学部第2問〜三角形と線分の長さの比
単元:
#数A#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
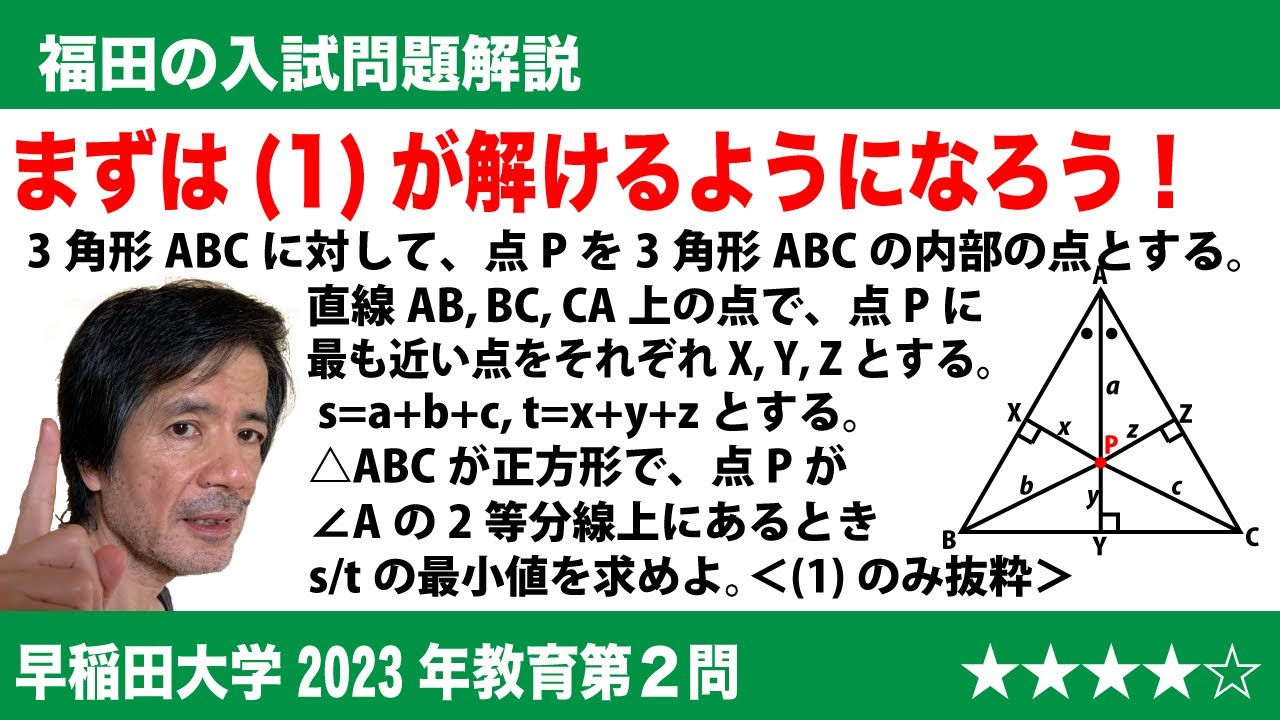
$\Large\boxed{2}$ 3角形ABCに対して、点Pを3角形ABCの内部の点とする。また、直線AB,BC,CA上の点で、点Pに最も近い点をそれぞれX,Y,Zとする。線分PA,PB,PCの長さをそれぞれ$a$,$b$,$c$とし、その和を$s$とする。線分PX,PY,PZの長さをそれぞれ$x$,$y$,$z$とし、その和を$t$とする。$\angle$APB=2$\gamma$とし、その2等分線と直線ABの交点をX'とする。このとき、次の問いに答えよ。
(1)3角形ABCは正3角形であり、点Pは$\angle$Aの2等分線にあるときの$\frac{s}{t}$の最小値を求めよ。
(2)線分PX'の長さを$a$,$b$,$\cos\gamma$を用いて表せ。
(3)3角形ABCと点P(ただし、点Pは3角形ABCの内部の点)を任意に動かすときの$\frac{s}{t}$の最小値を求めよ。$\angle$BPC=2$\alpha$, $\angle$CPA=2$\beta$としたとき、以下の不等式が成立することを利用してもよい。
$(a+b+c)-2(\sqrt{ab}\cos\gamma+\sqrt{bc}\cos\alpha\sqrt{ca}\cos\beta)$≧0
この動画を見る
$\Large\boxed{2}$ 3角形ABCに対して、点Pを3角形ABCの内部の点とする。また、直線AB,BC,CA上の点で、点Pに最も近い点をそれぞれX,Y,Zとする。線分PA,PB,PCの長さをそれぞれ$a$,$b$,$c$とし、その和を$s$とする。線分PX,PY,PZの長さをそれぞれ$x$,$y$,$z$とし、その和を$t$とする。$\angle$APB=2$\gamma$とし、その2等分線と直線ABの交点をX'とする。このとき、次の問いに答えよ。
(1)3角形ABCは正3角形であり、点Pは$\angle$Aの2等分線にあるときの$\frac{s}{t}$の最小値を求めよ。
(2)線分PX'の長さを$a$,$b$,$\cos\gamma$を用いて表せ。
(3)3角形ABCと点P(ただし、点Pは3角形ABCの内部の点)を任意に動かすときの$\frac{s}{t}$の最小値を求めよ。$\angle$BPC=2$\alpha$, $\angle$CPA=2$\beta$としたとき、以下の不等式が成立することを利用してもよい。
$(a+b+c)-2(\sqrt{ab}\cos\gamma+\sqrt{bc}\cos\alpha\sqrt{ca}\cos\beta)$≧0
福田の数学〜早稲田大学2023年教育学部第1問(4)〜三角形の面積の最大Part2

単元:
#数A#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)辺の長さが3,4,5の3角形がある。それぞれの辺の中点上に3つの点A,B,Cがあり、ある時刻から同時に動き出し、3点とも反時計回りに速さ1で3角形の周上を回る(ある辺から頂点に到達したらその頂点を含む別の辺へと進む)とする。3角形ABCの面積が最大になるときの面積を求めよ。
この動画を見る
$\Large\boxed{1}$ (4)辺の長さが3,4,5の3角形がある。それぞれの辺の中点上に3つの点A,B,Cがあり、ある時刻から同時に動き出し、3点とも反時計回りに速さ1で3角形の周上を回る(ある辺から頂点に到達したらその頂点を含む別の辺へと進む)とする。3角形ABCの面積が最大になるときの面積を求めよ。
福田の数学〜早稲田大学2023年教育学部第1問(4)〜三角形の面積の最大Part1

単元:
#数A#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)辺の長さが3,4,5の3角形がある。それぞれの辺の中点上に3つの点A,B,Cがあり、ある時刻から同時に動き出し、3点とも反時計回りに速さ1で3角形の周上を回る(ある辺から頂点に到達したらその頂点を含む別の辺へと進む)とする。3角形ABCの面積が最大になるときの面積を求めよ。
この動画を見る
$\Large\boxed{1}$ (4)辺の長さが3,4,5の3角形がある。それぞれの辺の中点上に3つの点A,B,Cがあり、ある時刻から同時に動き出し、3点とも反時計回りに速さ1で3角形の周上を回る(ある辺から頂点に到達したらその頂点を含む別の辺へと進む)とする。3角形ABCの面積が最大になるときの面積を求めよ。
福田の数学〜早稲田大学2023年教育学部第1問(3)〜連立漸化式と複素数平面

単元:
#大学入試過去問(数学)#複素数平面#数列#漸化式#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
$x_0=0,y_0=-1$のとき、非負整数$n\geqq 0$に対して、
$x_{n+1}=(\cos \frac{3\pi}{11})x_n-(\sin \frac{3\pi}{11)}y_n$
$y_{n+1}=(\cos \frac{3\pi}{11})x_n+(\sin \frac{3\pi}{11)}y_n$
のとき、$x_n$が最小となる最初のnを求めよ。
2023早稲田大学教育学部過去問
この動画を見る
$x_0=0,y_0=-1$のとき、非負整数$n\geqq 0$に対して、
$x_{n+1}=(\cos \frac{3\pi}{11})x_n-(\sin \frac{3\pi}{11)}y_n$
$y_{n+1}=(\cos \frac{3\pi}{11})x_n+(\sin \frac{3\pi}{11)}y_n$
のとき、$x_n$が最小となる最初のnを求めよ。
2023早稲田大学教育学部過去問
福田の数学〜早稲田大学2023年教育学部第1問(2)〜袋から球を取り出す確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)袋の中に赤玉5個と白玉5個が入っている。次の規則に従って袋から玉を無作為に取り出す。
ステップ1. 袋から玉を3個取り出す。
ステップ2. ステップ1で取り出した玉の中に含まれている赤玉の数と同じ数の玉を袋から取り出す。
このとき、2回取り出した玉の中で赤玉が合計3個となる事象の確率を求めよ。
ただし、ステップ1の後、取り出された玉を袋に戻さない。
この動画を見る
$\Large\boxed{1}$ (2)袋の中に赤玉5個と白玉5個が入っている。次の規則に従って袋から玉を無作為に取り出す。
ステップ1. 袋から玉を3個取り出す。
ステップ2. ステップ1で取り出した玉の中に含まれている赤玉の数と同じ数の玉を袋から取り出す。
このとき、2回取り出した玉の中で赤玉が合計3個となる事象の確率を求めよ。
ただし、ステップ1の後、取り出された玉を袋に戻さない。
福田の数学〜早稲田大学2023年教育学部第1問(1)〜外から引いた接線と三角形の面積の最大

単元:
#数A#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)0<$b$<100 を満たす実数$b$に対し、点(10,$b$)から放物線$C$:$y$=$x^2$に相異なる2本の接線を引き、この2本の接線の$C$における接点をそれぞれ$P_1$, $P_2$とする。実数$b$が0<$b$<100の範囲で動くとき、3角形$OP_1P_2$の面積の最大値を求めよ。ただし、Oは原点を表す。
この動画を見る
$\Large\boxed{1}$ (1)0<$b$<100 を満たす実数$b$に対し、点(10,$b$)から放物線$C$:$y$=$x^2$に相異なる2本の接線を引き、この2本の接線の$C$における接点をそれぞれ$P_1$, $P_2$とする。実数$b$が0<$b$<100の範囲で動くとき、3角形$OP_1P_2$の面積の最大値を求めよ。ただし、Oは原点を表す。
福田の数学〜東京理科大学2023年創域理工学部第3問〜対数関数と直線で囲まれた図形の面積

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 座標平面上で、曲線$y$=$\sqrt 5\log x$ ($x$>0)を$C$とし、$C$上の点A($a$, $\sqrt 5\log a$) ($a$>0)をとる。ただし、$\log$は自然対数とする。点Aにおける$C$の接線を$l$とし、$l$と$y$軸の交点をQ(0,$q$)とする。また、点Aにおける$C$の法線を$m$とし、$m$と$y$軸の交点をR(0,$r$)とする。
(1)$q$を、$a$を用いて表せ。
(2)$r$を、$a$を用いて表せ。
(3)線分QRの長さが$3\sqrt 5$となるような$a$の値を求めよ。
(4)$\angle$ARQ=$\frac{\pi}{6}$となるような$a$の値を求めよ。
(5)$a$=$e^2$とする。このとき、$x$軸、曲線$C$および直線$l$で囲まれた部分の面積を求めよ。ただし、$e$は自然対数の底である。
この動画を見る
$\Large\boxed{3}$ 座標平面上で、曲線$y$=$\sqrt 5\log x$ ($x$>0)を$C$とし、$C$上の点A($a$, $\sqrt 5\log a$) ($a$>0)をとる。ただし、$\log$は自然対数とする。点Aにおける$C$の接線を$l$とし、$l$と$y$軸の交点をQ(0,$q$)とする。また、点Aにおける$C$の法線を$m$とし、$m$と$y$軸の交点をR(0,$r$)とする。
(1)$q$を、$a$を用いて表せ。
(2)$r$を、$a$を用いて表せ。
(3)線分QRの長さが$3\sqrt 5$となるような$a$の値を求めよ。
(4)$\angle$ARQ=$\frac{\pi}{6}$となるような$a$の値を求めよ。
(5)$a$=$e^2$とする。このとき、$x$軸、曲線$C$および直線$l$で囲まれた部分の面積を求めよ。ただし、$e$は自然対数の底である。
福田の数学〜東京理科大学2023年創域理工学部第2問〜直線の交点と関数の最大

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 座標平面上に点A(2,0)と点B(0,1)がある。正の実数$t$に対して、$x$軸上の点P(2+$t$, 0)と$y$軸上の点Q(0, 1+$\displaystyle\frac{1}{t}$)を考える。
(1)直線AQの方程式を、$t$を用いて表せ。
(2)直線BPの方程式を、$t$を用いて表せ。
直線AQと直線BPの交点をR($u$,$v$)とする。
(3)$u$と$v$を、$t$を用いて表せ。
(4)$t$>0の範囲で、$u$+$v$の値を最大にする$t$の値を求めよ。
この動画を見る
$\Large\boxed{2}$ 座標平面上に点A(2,0)と点B(0,1)がある。正の実数$t$に対して、$x$軸上の点P(2+$t$, 0)と$y$軸上の点Q(0, 1+$\displaystyle\frac{1}{t}$)を考える。
(1)直線AQの方程式を、$t$を用いて表せ。
(2)直線BPの方程式を、$t$を用いて表せ。
直線AQと直線BPの交点をR($u$,$v$)とする。
(3)$u$と$v$を、$t$を用いて表せ。
(4)$t$>0の範囲で、$u$+$v$の値を最大にする$t$の値を求めよ。
福田の数学〜東京理科大学2023年創域理工学部第1問(3)〜偶奇で定義の異なる漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)数列$\left\{a_n\right\}$は、$a_1$=$\displaystyle\frac{7}{5}$, $n$が偶数の時は$a_{n+1}$=$\displaystyle\frac{1+a_n}{2}$, $n$が奇数の時は$a_{n+1}$=$\displaystyle\frac{2+a_n}{2}$を満たすとする。このとき、$a_2$=$\frac{\boxed{\ \ ヘホ\ \ }}{\boxed{\ \ マミ\ \ }}$, $a_3$=$\frac{\boxed{\ \ ムメ\ \ }}{\boxed{\ \ モヤ\ \ }}$である。
さらに、自然数$k$に対して$a_{2k+1}$=$\boxed{\ \ ユ\ \ }$+$\frac{\boxed{\ \ ヨ\ \ }}{\boxed{\ \ ラ\ \ }}a_{2k-1}$となる。これを
$a_{2k+1}$-$\frac{\boxed{\ \ リ\ \ }}{\boxed{\ \ ル\ \ }}$=$\frac{\boxed{\ \ レ\ \ }}{\boxed{\ \ ロ\ \ }}\left( a_{2k-1}-\frac{\boxed{\ \ リ\ \ }}{\boxed{\ \ ル\ \ }} \right)$
と変形することにより、
$a_{2k-1}$=$\frac{1}{\boxed{\ \ ワヲ\ \ }}\left( \frac{\boxed{\ \ レ\ \ }}{\boxed{\ \ ロ\ \ }} \right)^{k-1}$+$\frac{\boxed{\ \ リ\ \ }}{\boxed{\ \ ル\ \ }}$
が得られる。また、
$a_{2k}$=$\frac{1}{\boxed{\ \ ンあ\ \ }}\left( \frac{\boxed{\ \ い\ \ }}{\boxed{\ \ う\ \ }} \right)^{k-1}$+$\frac{\boxed{\ \ え\ \ }}{\boxed{\ \ お\ \ }}$
も得られる。
この動画を見る
$\Large\boxed{1}$ (3)数列$\left\{a_n\right\}$は、$a_1$=$\displaystyle\frac{7}{5}$, $n$が偶数の時は$a_{n+1}$=$\displaystyle\frac{1+a_n}{2}$, $n$が奇数の時は$a_{n+1}$=$\displaystyle\frac{2+a_n}{2}$を満たすとする。このとき、$a_2$=$\frac{\boxed{\ \ ヘホ\ \ }}{\boxed{\ \ マミ\ \ }}$, $a_3$=$\frac{\boxed{\ \ ムメ\ \ }}{\boxed{\ \ モヤ\ \ }}$である。
さらに、自然数$k$に対して$a_{2k+1}$=$\boxed{\ \ ユ\ \ }$+$\frac{\boxed{\ \ ヨ\ \ }}{\boxed{\ \ ラ\ \ }}a_{2k-1}$となる。これを
$a_{2k+1}$-$\frac{\boxed{\ \ リ\ \ }}{\boxed{\ \ ル\ \ }}$=$\frac{\boxed{\ \ レ\ \ }}{\boxed{\ \ ロ\ \ }}\left( a_{2k-1}-\frac{\boxed{\ \ リ\ \ }}{\boxed{\ \ ル\ \ }} \right)$
と変形することにより、
$a_{2k-1}$=$\frac{1}{\boxed{\ \ ワヲ\ \ }}\left( \frac{\boxed{\ \ レ\ \ }}{\boxed{\ \ ロ\ \ }} \right)^{k-1}$+$\frac{\boxed{\ \ リ\ \ }}{\boxed{\ \ ル\ \ }}$
が得られる。また、
$a_{2k}$=$\frac{1}{\boxed{\ \ ンあ\ \ }}\left( \frac{\boxed{\ \ い\ \ }}{\boxed{\ \ う\ \ }} \right)^{k-1}$+$\frac{\boxed{\ \ え\ \ }}{\boxed{\ \ お\ \ }}$
も得られる。
福田の数学〜東京理科大学2023年創域理工学部第1問(2)〜高次方程式と解と係数の関係

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)A, B, C, Dを定数とする。$f(x)$=$2x^3$-$9x^2$+$Ax$+$B$, $g(x)$=$x^2$-$Cx$-$D$
とおく。以下の問いに答えよ。
(a)$g(1-\sqrt 2)$=0 かつ $g(1+\sqrt 2)$=0のとき、$C$=$\boxed{\ \ セ\ \ }$, $D$=$\boxed{\ \ ソ\ \ }$である。また、$f(1-\sqrt 2)$=0 かつ $f(1+\sqrt 2)$=0のとき、$A$=$\boxed{\ \ タ\ \ }$, $B$=$\boxed{\ \ チ\ \ }$であり、方程式$f(x)$=0を満たす有理数$x$は
$x$=$\frac{\boxed{\ \ ツ\ \ }}{\boxed{\ \ テ\ \ }}$
である。
この動画を見る
$\Large\boxed{1}$ (2)A, B, C, Dを定数とする。$f(x)$=$2x^3$-$9x^2$+$Ax$+$B$, $g(x)$=$x^2$-$Cx$-$D$
とおく。以下の問いに答えよ。
(a)$g(1-\sqrt 2)$=0 かつ $g(1+\sqrt 2)$=0のとき、$C$=$\boxed{\ \ セ\ \ }$, $D$=$\boxed{\ \ ソ\ \ }$である。また、$f(1-\sqrt 2)$=0 かつ $f(1+\sqrt 2)$=0のとき、$A$=$\boxed{\ \ タ\ \ }$, $B$=$\boxed{\ \ チ\ \ }$であり、方程式$f(x)$=0を満たす有理数$x$は
$x$=$\frac{\boxed{\ \ ツ\ \ }}{\boxed{\ \ テ\ \ }}$
である。
福田の数学〜東京理科大学2023年創域理工学部第1問(1)〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)(a)1個のさいころを4回続けて投げるとき、4回とも同じ目が出る確率は
$\displaystyle\frac{1}{\boxed{\ \ アイウ\ \ }}$であり、3, 4, 5, 6の目がそれぞれ1回ずつ出る確率は$\displaystyle\frac{1}{\boxed{\ \ エオ\ \ }}$である。
(b)1個のさいころを4回続けて投げて、出た目を順に左から並べて4桁の整数Nを作る。例えば、1回目に2、2回目に6、3回目に1、4回目に2の目がでた場合はN=2612である。Nが偶数となる確率は$\displaystyle\frac{1}{\boxed{\ \ カ\ \ }}$であり、N≧2023 となる確率は$\displaystyle\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$であり、N≧5555 となる確率は$\displaystyle\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシス\ \ }}$である。
この動画を見る
$\Large\boxed{1}$ (1)(a)1個のさいころを4回続けて投げるとき、4回とも同じ目が出る確率は
$\displaystyle\frac{1}{\boxed{\ \ アイウ\ \ }}$であり、3, 4, 5, 6の目がそれぞれ1回ずつ出る確率は$\displaystyle\frac{1}{\boxed{\ \ エオ\ \ }}$である。
(b)1個のさいころを4回続けて投げて、出た目を順に左から並べて4桁の整数Nを作る。例えば、1回目に2、2回目に6、3回目に1、4回目に2の目がでた場合はN=2612である。Nが偶数となる確率は$\displaystyle\frac{1}{\boxed{\ \ カ\ \ }}$であり、N≧2023 となる確率は$\displaystyle\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$であり、N≧5555 となる確率は$\displaystyle\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシス\ \ }}$である。
福田の数学〜中央大学2023年理工学部第4問〜関数方程式

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 以下の問いに答えよ。
(1)整式$f(x)$=$a_nx^n$+$a_{n-1}x^{n-1}$+...+$a_1x$+$a_0$ ($a_0$≠0)に対し、
$f(x+1)$-$f(x)$=$b_nx^n$+$b_{n-1}x^{n-1}$+...+$b_1x$+$b_0$ ($a_0$≠0)
と表すとき、$b_n$と$b_{n-1}$を求めよ。
(2)整式$g(x)$が恒等式$g(x+1)$-$g(x)$=$(x-1)x(x+1)$および$g(0)$=0を満たすとき、$g(x)$を求めよ。
(3)整式$h(x)$が恒等式$h(2x+1)$-$h(2x)$=$h(x)$-$x^2$を満たすとき、$h(x)$を求めよ。
この動画を見る
$\Large\boxed{4}$ 以下の問いに答えよ。
(1)整式$f(x)$=$a_nx^n$+$a_{n-1}x^{n-1}$+...+$a_1x$+$a_0$ ($a_0$≠0)に対し、
$f(x+1)$-$f(x)$=$b_nx^n$+$b_{n-1}x^{n-1}$+...+$b_1x$+$b_0$ ($a_0$≠0)
と表すとき、$b_n$と$b_{n-1}$を求めよ。
(2)整式$g(x)$が恒等式$g(x+1)$-$g(x)$=$(x-1)x(x+1)$および$g(0)$=0を満たすとき、$g(x)$を求めよ。
(3)整式$h(x)$が恒等式$h(2x+1)$-$h(2x)$=$h(x)$-$x^2$を満たすとき、$h(x)$を求めよ。
福田の数学〜中央大学2023年理工学部第3問〜関数の変曲点と面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $f(x)=\displaystyle\frac{1}{1+e^{-x}}$とし、曲線$y$=$f(x)$をCとする。以下の問いに答えよ。
(1)曲線Cの変曲点Pの座標を求めよ。
(2)曲線Cの点Pにおける接線$l$の方程式を求めよ。また、直線$l$と直線$y$=1の交点の$x$座標$a$を求めよ。
(3)$b$を(2)で求めた$a$より大きい実数とする。曲線Cと直線$y$=1, $x$=$a$, $x$=$b$で囲まれた部分の面積$S(b)$を求めよ。
(4)$\displaystyle\lim_{b \to \infty}S(b)$を求めよ。
この動画を見る
$\Large\boxed{3}$ $f(x)=\displaystyle\frac{1}{1+e^{-x}}$とし、曲線$y$=$f(x)$をCとする。以下の問いに答えよ。
(1)曲線Cの変曲点Pの座標を求めよ。
(2)曲線Cの点Pにおける接線$l$の方程式を求めよ。また、直線$l$と直線$y$=1の交点の$x$座標$a$を求めよ。
(3)$b$を(2)で求めた$a$より大きい実数とする。曲線Cと直線$y$=1, $x$=$a$, $x$=$b$で囲まれた部分の面積$S(b)$を求めよ。
(4)$\displaystyle\lim_{b \to \infty}S(b)$を求めよ。
福田の数学〜中央大学2023年理工学部第2問〜三角関数の近似値

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ (1)$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{6}$のとき、関数$\displaystyle\frac{\sin x}{x}$は$\boxed{\ \ サ\ \ }$する。このことより、
$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{6}$では$\boxed{\ \ シ\ \ }$≦$\displaystyle\frac{\sin x}{x}$≦$\boxed{\ \ シ\ \ }$+0.05 が成り立つ。
$\boxed{\ \ サ\ \ }$の解答群
ⓐ 区間$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{6}$で増加 ⓑ区間$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{6}$で減少
ⓒ区間$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{8}$で増加し、区間$\displaystyle\frac{\pi}{8}$≦$x$≦$\displaystyle\frac{\pi}{6}$で減少
ⓓ区間$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{8}$で減少し、区間$\displaystyle\frac{\pi}{8}$≦$x$≦$\displaystyle\frac{\pi}{6}$で増加
ⓔ区間$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{2}$で増加し、区間$\displaystyle\frac{\pi}{2}$≦$x$≦$\displaystyle\frac{\pi}{6}$で減少
ⓕ区間$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{2}$で減少し、区間$\displaystyle\frac{\pi}{2}$≦$x$≦$\displaystyle\frac{\pi}{6}$で増加
$\boxed{\ \ シ\ \ }$の解答群
ⓐ0.8 ⓑ0.85 ⓒ0.9 ⓓ0.95 ⓔ1 ⓕ1.05 ⓖ1.1 ⓗ1.15
(2)底面が正五角形PQRSTで、側面が正三角形である正五角錐をKとする。ただし、Kの各辺の長さを1とする。底面にはないKの頂点をAとし、線分PQの中点をMとする。また線分PSの長さは$\boxed{\ \ ス\ \ }$である。これより、$\cos\angle SAM$の値は
$\boxed{\ \ セ\ \ }$-0.025≦$\cos\angle SAM$<$\boxed{\ \ セ\ \ }$+0.025
を満たす。さらに、(1)の$\displaystyle\frac{\sin x}{x}$についての結果より、$\angle SAM$の大きさは
$\boxed{\ \ ソ\ \ }$-1.5°≦$\cos\angle SAM$<$\boxed{\ \ ソ\ \ }$+1.5°
を満たす。
なお、必要ならば$\sqrt 2$=1.41..., $\sqrt 3$=1.73..., $\sqrt 5$=2.23... を用いてよい。
$\boxed{\ \ ス\ \ }$の解答群
ⓐ$\sqrt 2$ ⓑ$\sqrt 3$ ⓒ$\sqrt 5$ ⓓ$\displaystyle\frac{1+\sqrt 2}{2}$
ⓔ$\displaystyle\frac{1+\sqrt 3}{2}$ ⓕ$\displaystyle\frac{1+\sqrt 5}{2}$ ⓖ$\displaystyle\frac{\sqrt 2+\sqrt 3}{2}$ ⓗ$\displaystyle\frac{\sqrt 2+\sqrt 5}{2}$
ⓘ$\displaystyle\frac{\sqrt 3+\sqrt 5}{2}$ ⓙ$\displaystyle\frac{\sqrt 2+\sqrt 3}{3}$ ⓚ$\displaystyle\frac{\sqrt 2+\sqrt 5}{3}$ ⓛ$\displaystyle\frac{\sqrt 3+\sqrt 5}{3}$
$\boxed{\ \ セ\ \ }$の解答群
ⓐ-0.4 ⓑ-0.35 ⓒ-0.3 ⓓ-0.25 ⓔ-0.2 ⓕ-0.15 ⓖ-0.1
$\boxed{\ \ ソ\ \ }$の解答群
ⓐ105° ⓑ108° ⓒ111° ⓓ114° ⓔ117° ⓕ120°
この動画を見る
$\Large\boxed{2}$ (1)$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{6}$のとき、関数$\displaystyle\frac{\sin x}{x}$は$\boxed{\ \ サ\ \ }$する。このことより、
$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{6}$では$\boxed{\ \ シ\ \ }$≦$\displaystyle\frac{\sin x}{x}$≦$\boxed{\ \ シ\ \ }$+0.05 が成り立つ。
$\boxed{\ \ サ\ \ }$の解答群
ⓐ 区間$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{6}$で増加 ⓑ区間$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{6}$で減少
ⓒ区間$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{8}$で増加し、区間$\displaystyle\frac{\pi}{8}$≦$x$≦$\displaystyle\frac{\pi}{6}$で減少
ⓓ区間$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{8}$で減少し、区間$\displaystyle\frac{\pi}{8}$≦$x$≦$\displaystyle\frac{\pi}{6}$で増加
ⓔ区間$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{2}$で増加し、区間$\displaystyle\frac{\pi}{2}$≦$x$≦$\displaystyle\frac{\pi}{6}$で減少
ⓕ区間$\displaystyle\frac{\pi}{12}$≦$x$≦$\displaystyle\frac{\pi}{2}$で減少し、区間$\displaystyle\frac{\pi}{2}$≦$x$≦$\displaystyle\frac{\pi}{6}$で増加
$\boxed{\ \ シ\ \ }$の解答群
ⓐ0.8 ⓑ0.85 ⓒ0.9 ⓓ0.95 ⓔ1 ⓕ1.05 ⓖ1.1 ⓗ1.15
(2)底面が正五角形PQRSTで、側面が正三角形である正五角錐をKとする。ただし、Kの各辺の長さを1とする。底面にはないKの頂点をAとし、線分PQの中点をMとする。また線分PSの長さは$\boxed{\ \ ス\ \ }$である。これより、$\cos\angle SAM$の値は
$\boxed{\ \ セ\ \ }$-0.025≦$\cos\angle SAM$<$\boxed{\ \ セ\ \ }$+0.025
を満たす。さらに、(1)の$\displaystyle\frac{\sin x}{x}$についての結果より、$\angle SAM$の大きさは
$\boxed{\ \ ソ\ \ }$-1.5°≦$\cos\angle SAM$<$\boxed{\ \ ソ\ \ }$+1.5°
を満たす。
なお、必要ならば$\sqrt 2$=1.41..., $\sqrt 3$=1.73..., $\sqrt 5$=2.23... を用いてよい。
$\boxed{\ \ ス\ \ }$の解答群
ⓐ$\sqrt 2$ ⓑ$\sqrt 3$ ⓒ$\sqrt 5$ ⓓ$\displaystyle\frac{1+\sqrt 2}{2}$
ⓔ$\displaystyle\frac{1+\sqrt 3}{2}$ ⓕ$\displaystyle\frac{1+\sqrt 5}{2}$ ⓖ$\displaystyle\frac{\sqrt 2+\sqrt 3}{2}$ ⓗ$\displaystyle\frac{\sqrt 2+\sqrt 5}{2}$
ⓘ$\displaystyle\frac{\sqrt 3+\sqrt 5}{2}$ ⓙ$\displaystyle\frac{\sqrt 2+\sqrt 3}{3}$ ⓚ$\displaystyle\frac{\sqrt 2+\sqrt 5}{3}$ ⓛ$\displaystyle\frac{\sqrt 3+\sqrt 5}{3}$
$\boxed{\ \ セ\ \ }$の解答群
ⓐ-0.4 ⓑ-0.35 ⓒ-0.3 ⓓ-0.25 ⓔ-0.2 ⓕ-0.15 ⓖ-0.1
$\boxed{\ \ ソ\ \ }$の解答群
ⓐ105° ⓑ108° ⓒ111° ⓓ114° ⓔ117° ⓕ120°
福田の数学〜中央大学2023年理工学部第1問〜複素数平面と確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#複素数平面#確率#複素数平面#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ さいころを2回ふって出た目の数を順に$a$, $b$とし、複素数$\alpha$, $\beta$を
$\alpha$=$\displaystyle\cos\frac{a\pi}{3}$+$\displaystyle i\sin\frac{a\pi}{3}$, $\beta$=$\displaystyle\cos\frac{b\pi}{3}$+$\displaystyle i\sin\frac{b\pi}{3}$
と定める($i$は虚数単位)。また、$\alpha$-$\beta$の絶対値を$d$=|$\alpha$-$\beta$|とおく。
(1)$d$のとりうる値は、小さいものから順に0, $\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$, $\boxed{\ \ ウ\ \ }$である。
$d$=0, $\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$, $\boxed{\ \ ウ\ \ }$が成り立つ確率はそれぞれ$\boxed{\ \ エ\ \ }$, $\boxed{\ \ オ\ \ }$, $\boxed{\ \ カ\ \ }$, $\boxed{\ \ キ\ \ }$である。
(2)$\alpha$-$\beta$が実数となる確率は$\boxed{\ \ ク\ \ }$であり、$\alpha$-$\beta$が実数という条件の下で$d$<$\boxed{\ \ ウ\ \ }$が成り立つ条件付き確率は$\boxed{\ \ ケ\ \ }$である。
(3)$\alpha^2$=$\beta^3$という条件の下で$\alpha+\beta$の虚部が正となる条件付き確率は$\boxed{\ \ コ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ さいころを2回ふって出た目の数を順に$a$, $b$とし、複素数$\alpha$, $\beta$を
$\alpha$=$\displaystyle\cos\frac{a\pi}{3}$+$\displaystyle i\sin\frac{a\pi}{3}$, $\beta$=$\displaystyle\cos\frac{b\pi}{3}$+$\displaystyle i\sin\frac{b\pi}{3}$
と定める($i$は虚数単位)。また、$\alpha$-$\beta$の絶対値を$d$=|$\alpha$-$\beta$|とおく。
(1)$d$のとりうる値は、小さいものから順に0, $\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$, $\boxed{\ \ ウ\ \ }$である。
$d$=0, $\boxed{\ \ ア\ \ }$, $\boxed{\ \ イ\ \ }$, $\boxed{\ \ ウ\ \ }$が成り立つ確率はそれぞれ$\boxed{\ \ エ\ \ }$, $\boxed{\ \ オ\ \ }$, $\boxed{\ \ カ\ \ }$, $\boxed{\ \ キ\ \ }$である。
(2)$\alpha$-$\beta$が実数となる確率は$\boxed{\ \ ク\ \ }$であり、$\alpha$-$\beta$が実数という条件の下で$d$<$\boxed{\ \ ウ\ \ }$が成り立つ条件付き確率は$\boxed{\ \ ケ\ \ }$である。
(3)$\alpha^2$=$\beta^3$という条件の下で$\alpha+\beta$の虚部が正となる条件付き確率は$\boxed{\ \ コ\ \ }$である。
福田の数学〜中央大学2023年経済学部第3問〜直方体の体積の最大

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ Oを原点とする座標空間内に点A($a$, 0, 0), B(0, $b$, 0)と線分AB上を動く点Pがある。ただし、$a$, $b$は正の定数とする。Pを通り$x$軸に垂直な直線と$x$軸との交点をQ、Pを通り$y$軸に垂直な直線と$y$軸との交点をRとする。長方形OQPRを底面とし、高さがOQの長さに等しい直方体の体積をVとおく。Pの座標をP($x$, $y$, 0)とするとき、以下の問いに答えよ。
(1)$y$を$x$を用いて表せ。
(2)Vを$x$を用いて表せ。
(3)Pが線分AB上を動くとき、Vの最大値を求めよ。また、そのときのPの座標を求めよ。
この動画を見る
$\Large\boxed{3}$ Oを原点とする座標空間内に点A($a$, 0, 0), B(0, $b$, 0)と線分AB上を動く点Pがある。ただし、$a$, $b$は正の定数とする。Pを通り$x$軸に垂直な直線と$x$軸との交点をQ、Pを通り$y$軸に垂直な直線と$y$軸との交点をRとする。長方形OQPRを底面とし、高さがOQの長さに等しい直方体の体積をVとおく。Pの座標をP($x$, $y$, 0)とするとき、以下の問いに答えよ。
(1)$y$を$x$を用いて表せ。
(2)Vを$x$を用いて表せ。
(3)Pが線分AB上を動くとき、Vの最大値を求めよ。また、そのときのPの座標を求めよ。
福田の数学〜中央大学2023年経済学部第2問〜確率漸化式

単元:
#数A#場合の数と確率#確率#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 正の整数$a$を入力すると0以上$a$以下の整数のどれか1つを等しい確率で出力する装置がある。この装置に$a$=10を入力する操作を$n$回繰り返す。出力された$n$個の整数の和が偶数となる確率を$p_n$、奇数となる確率を$q_n$とするとき、以下の問いに答えよ。
(1)$p_1$, $q_1$を求めよ。
(2)$p_{n+1}$を$p_n$, $q_n$を用いて表せ。
(3)$p_n$を$n$の式で表せ。
この動画を見る
$\Large\boxed{2}$ 正の整数$a$を入力すると0以上$a$以下の整数のどれか1つを等しい確率で出力する装置がある。この装置に$a$=10を入力する操作を$n$回繰り返す。出力された$n$個の整数の和が偶数となる確率を$p_n$、奇数となる確率を$q_n$とするとき、以下の問いに答えよ。
(1)$p_1$, $q_1$を求めよ。
(2)$p_{n+1}$を$p_n$, $q_n$を用いて表せ。
(3)$p_n$を$n$の式で表せ。
福田の数学〜中央大学2023年経済学部第1問(6)〜絶対値の付いた定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の定積分の値を求めよ。
$\displaystyle \int_{0}^{4} |x^2-2x-3| dx$
2023中央大学経済学部過去問
この動画を見る
次の定積分の値を求めよ。
$\displaystyle \int_{0}^{4} |x^2-2x-3| dx$
2023中央大学経済学部過去問
福田の数学〜中央大学2023年経済学部第1問(5)〜平面ベクトルの成分と絶対値

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#平面上のベクトル#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\vec{a}+\vec{b}=(3,4),\vec{a}-\vec{b}=(1,2)$
のとき
$|2\vec{a}-3\vec{b}|$
の値を求めよ。
2023中央大学経済学部過去問
この動画を見る
$\vec{a}+\vec{b}=(3,4),\vec{a}-\vec{b}=(1,2)$
のとき
$|2\vec{a}-3\vec{b}|$
の値を求めよ。
2023中央大学経済学部過去問



