 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田のわかった数学〜高校3年生理系062〜微分(7)多重因子(1)

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(7) 多重因子(1)
整式$f(x)$が$(x-\alpha)^3$で割り切れる$\iff f(a)=f'(a)=f''(a)=0$
であることを示せ。
この動画を見る
数学$\textrm{III}$ 微分(7) 多重因子(1)
整式$f(x)$が$(x-\alpha)^3$で割り切れる$\iff f(a)=f'(a)=f''(a)=0$
であることを示せ。
福田の数学〜慶應義塾大学2021年看護医療学部第4問〜空間ベクトルと三角形の面積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$ $P(0,0,-1),\ Q(0,1,-2),\ R(1,0,-2)$を頂点とする三角形の面積は$\boxed{\ \ ヘ\ \ }$である。
aを実数とし、$\overrightarrow{ v }=(a,a,3)$とする。点P',Q',R'を
$\overrightarrow{ OP' }=\overrightarrow{ OP }+\overrightarrow{ v },\ \overrightarrow{ OQ' }=\overrightarrow{ OQ }+\overrightarrow{ v },\ \overrightarrow{ OR' }=$
$\overrightarrow{ OR }+\overrightarrow{ v }$
によって定め、さらに線分$PP',QQ',RR'$が$xy$平面と交わる点を$P'',Q'',R''$とする。
このとき、$P''$の座標は$\boxed{\ \ ホ\ \ }$、$Q''$の座標は$\boxed{\ \ マ\ \ }$、$R''$の座標は$\boxed{\ \ ミ\ \ }$である。
$\triangle P''Q''R''$が正三角形になるのは$a=\boxed{\ \ ム\ \ }$のときである。
3点$P'',Q'',R''$が同一直線上にあるのは$a=\boxed{\ \ メ\ \ }$のときである。$a \gt \boxed{\ \ メ\ \ }$のとき、
$\triangle P''Q''R''$の面積を$a$で表すと$\boxed{\ \ モ\ \ }$となる。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{4}}$ $P(0,0,-1),\ Q(0,1,-2),\ R(1,0,-2)$を頂点とする三角形の面積は$\boxed{\ \ ヘ\ \ }$である。
aを実数とし、$\overrightarrow{ v }=(a,a,3)$とする。点P',Q',R'を
$\overrightarrow{ OP' }=\overrightarrow{ OP }+\overrightarrow{ v },\ \overrightarrow{ OQ' }=\overrightarrow{ OQ }+\overrightarrow{ v },\ \overrightarrow{ OR' }=$
$\overrightarrow{ OR }+\overrightarrow{ v }$
によって定め、さらに線分$PP',QQ',RR'$が$xy$平面と交わる点を$P'',Q'',R''$とする。
このとき、$P''$の座標は$\boxed{\ \ ホ\ \ }$、$Q''$の座標は$\boxed{\ \ マ\ \ }$、$R''$の座標は$\boxed{\ \ ミ\ \ }$である。
$\triangle P''Q''R''$が正三角形になるのは$a=\boxed{\ \ ム\ \ }$のときである。
3点$P'',Q'',R''$が同一直線上にあるのは$a=\boxed{\ \ メ\ \ }$のときである。$a \gt \boxed{\ \ メ\ \ }$のとき、
$\triangle P''Q''R''$の面積を$a$で表すと$\boxed{\ \ モ\ \ }$となる。
2021慶應義塾大学看護医療学部過去問
福田のわかった数学〜高校2年生045〜軌跡(12)2本の直交する接線が引ける点の軌跡

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 軌跡(12) 接線直交
点Pは放物線$C:y=x^2$へ2本の接線が引け、その2本の
接線は直交するという。そのような点Pの軌跡を求めよ。
この動画を見る
数学$\textrm{II}$ 軌跡(12) 接線直交
点Pは放物線$C:y=x^2$へ2本の接線が引け、その2本の
接線は直交するという。そのような点Pの軌跡を求めよ。
福田の数学〜慶應義塾大学2021年看護医療学部第3問〜散布図と箱ひげ図

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$ある高校の生徒30人に対し、50m走のタイムを2回計測した。
左図(※動画参照)は1回目の計測結果を横軸に2回目の計測結果
を縦軸に取った散布図である。
(1)次の$(\textrm{A})$から$(\textrm{F})$のうち、1回目の計測結果の箱ひげ図
として適当なものは$\boxed{\ \ ネ\ \ }$であり、2回目の計測結果の箱ひげ図として
適当なものは$\boxed{\ \ ノ\ \ }$である。
(2)次の$(\textrm{G})$から$(\textrm{L})$のうち、1回目と2回目の計測結果の合計の
箱ひげ図として適切なものは$\boxed{\ \ ハ\ \ }$である。
(3)遅れてやってきた31人目の生徒の50m走のタイムを2回計測した
結果、1回目は20.0(秒)、2回目は10.0(秒)であった。各生徒の2回の\\
計測結果の合計を考え、最初の30人の生徒の平均値を$\bar{ x_{31} }$,中央値を
$m_{31}$とする。$\bar{ x_{30} }=17.0$であることに注意すると、
$\bar{ x_{31} }-\bar{ x_{30} }=\boxed{\ \ ヒ\ \ }$である。一方、
$m_{31}-m_{30}=\boxed{\ \ フ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{3}}$ある高校の生徒30人に対し、50m走のタイムを2回計測した。
左図(※動画参照)は1回目の計測結果を横軸に2回目の計測結果
を縦軸に取った散布図である。
(1)次の$(\textrm{A})$から$(\textrm{F})$のうち、1回目の計測結果の箱ひげ図
として適当なものは$\boxed{\ \ ネ\ \ }$であり、2回目の計測結果の箱ひげ図として
適当なものは$\boxed{\ \ ノ\ \ }$である。
(2)次の$(\textrm{G})$から$(\textrm{L})$のうち、1回目と2回目の計測結果の合計の
箱ひげ図として適切なものは$\boxed{\ \ ハ\ \ }$である。
(3)遅れてやってきた31人目の生徒の50m走のタイムを2回計測した
結果、1回目は20.0(秒)、2回目は10.0(秒)であった。各生徒の2回の\\
計測結果の合計を考え、最初の30人の生徒の平均値を$\bar{ x_{31} }$,中央値を
$m_{31}$とする。$\bar{ x_{30} }=17.0$であることに注意すると、
$\bar{ x_{31} }-\bar{ x_{30} }=\boxed{\ \ ヒ\ \ }$である。一方、
$m_{31}-m_{30}=\boxed{\ \ フ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
福田のわかった数学〜高校3年生理系061〜微分(6)高次導関数

単元:
#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(6) 高次導関数
$f(x)=\sin x$の第$n$次導関数は
$f^{(n)}(x)=\sin(x+\frac{n\pi}{2})$であることを示せ。
この動画を見る
数学$\textrm{III}$ 微分(6) 高次導関数
$f(x)=\sin x$の第$n$次導関数は
$f^{(n)}(x)=\sin(x+\frac{n\pi}{2})$であることを示せ。
福田の数学〜慶應義塾大学2021年看護医療学部第2問(3)〜絶対値の付いた2次不等式の解

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(3)aを正の定数とし、不等式
$|x^2-ax+3| \leqq 1$
の解を実数の範囲で考える。
0 $\lt a \lt \boxed{\ \ ナ\ \ }$のとき、この不等式の解は存在しない。
$\boxed{\ \ ナ\ \ } \leqq a \leqq \boxed{\ \ ニ\ \ }$のとき、この不等式の解は
ある実数$p,q$によって$p \leqq x \leqq q$と表される。
$a \gt \boxed{\ \ ニ\ \ }$のときこの不等式の解は$\boxed{\ \ ヌ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{2}}$(3)aを正の定数とし、不等式
$|x^2-ax+3| \leqq 1$
の解を実数の範囲で考える。
0 $\lt a \lt \boxed{\ \ ナ\ \ }$のとき、この不等式の解は存在しない。
$\boxed{\ \ ナ\ \ } \leqq a \leqq \boxed{\ \ ニ\ \ }$のとき、この不等式の解は
ある実数$p,q$によって$p \leqq x \leqq q$と表される。
$a \gt \boxed{\ \ ニ\ \ }$のときこの不等式の解は$\boxed{\ \ ヌ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
福田のわかった数学〜高校1年生045〜三角形への応用(2)
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
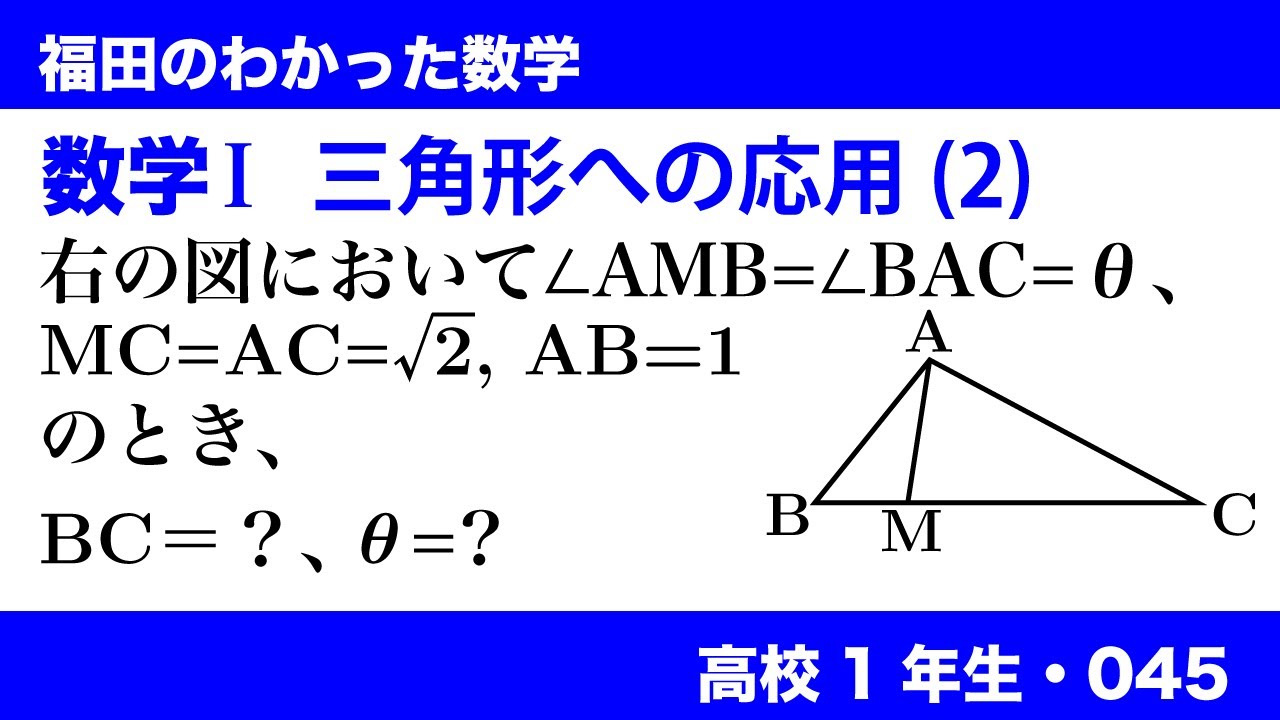
数学$\textrm{I}$ 三角形への応用(2)
右の図(※動画参照)において$\angle AMB=\angle BAC=\theta$、
$MC=AC=\sqrt2, AB=1$のとき
$BC$を求め、$\theta$の値を求めよ。
この動画を見る
数学$\textrm{I}$ 三角形への応用(2)
右の図(※動画参照)において$\angle AMB=\angle BAC=\theta$、
$MC=AC=\sqrt2, AB=1$のとき
$BC$を求め、$\theta$の値を求めよ。
福田の数学〜慶應義塾大学2021年看護医療学部第2問(2)〜外接する円に接する直線

単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(2)円$x^2+y^2=1$をCと表す。$p \gt 1$とし、点P(0,p)を通るCの2つの接線
を$l_1,l_2$とする。$l_1,l_2$の方程式は
$y=\boxed{\ \ タ\ \ }, y=\boxed{\ \ チ\ \ }$
であり、$l_1,l_2$が直交するのは$p=\boxed{\ \ ツ\ \ }$のときである。
$p=\boxed{\ \ ツ\ \ }$のとき、$l_1,l_2$を接線に持ち、かつCに外接する円の中で中心が
y軸上にある2つの円の半径は$\boxed{\ \ テ\ \ }$および$\boxed{\ \ ト\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{2}}$(2)円$x^2+y^2=1$をCと表す。$p \gt 1$とし、点P(0,p)を通るCの2つの接線
を$l_1,l_2$とする。$l_1,l_2$の方程式は
$y=\boxed{\ \ タ\ \ }, y=\boxed{\ \ チ\ \ }$
であり、$l_1,l_2$が直交するのは$p=\boxed{\ \ ツ\ \ }$のときである。
$p=\boxed{\ \ ツ\ \ }$のとき、$l_1,l_2$を接線に持ち、かつCに外接する円の中で中心が
y軸上にある2つの円の半径は$\boxed{\ \ テ\ \ }$および$\boxed{\ \ ト\ \ }$である。
2021慶應義塾大学看護医療学部過去問
福田のわかった数学〜高校3年生理系060〜微分(5)陰関数の微分(2)

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(5) 陰関数の微分(2)
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 上の点$(p,q)$での接線の方程式
は $\frac{px}{a^2}+\frac{qy}{b^2}=1$ であることを示せ。
この動画を見る
数学$\textrm{III}$ 微分(5) 陰関数の微分(2)
$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ 上の点$(p,q)$での接線の方程式
は $\frac{px}{a^2}+\frac{qy}{b^2}=1$ であることを示せ。
福田の数学〜慶應義塾大学2021年看護医療学部第2問(1)〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$ (1)座標平面上を動く点Pが原点の位置がある。1個のさいころを投げて、1または2の
目が出たときには、Pはx軸の正の向きに1だけ進み、他の目が出たときには、
Pはy軸の正の向きに2だけ進むことにして、さいころを3回投げる。
点Pの座標が(2,2)である確率は$\boxed{\ \ ス\ \ }$であり、Pと原点との距離が3以上である
確率は$\boxed{\ \ セ\ \ }$である。Pと原点との距離が3以上という条件の下で、Pが座標軸上にない
条件付確率は$\boxed{\ \ ソ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{2}}$ (1)座標平面上を動く点Pが原点の位置がある。1個のさいころを投げて、1または2の
目が出たときには、Pはx軸の正の向きに1だけ進み、他の目が出たときには、
Pはy軸の正の向きに2だけ進むことにして、さいころを3回投げる。
点Pの座標が(2,2)である確率は$\boxed{\ \ ス\ \ }$であり、Pと原点との距離が3以上である
確率は$\boxed{\ \ セ\ \ }$である。Pと原点との距離が3以上という条件の下で、Pが座標軸上にない
条件付確率は$\boxed{\ \ ソ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
福田のわかった数学〜高校2年生044〜軌跡(11)中点の軌跡(2)

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 軌跡(11) 中点の軌跡(2)
円$x^2+y^2=1$ と直線$y=m(x-2)$が
異なる2点A,Bで交わるとき、
線分ABの中点Mの軌跡を求めよ。
この動画を見る
数学$\textrm{II}$ 軌跡(11) 中点の軌跡(2)
円$x^2+y^2=1$ と直線$y=m(x-2)$が
異なる2点A,Bで交わるとき、
線分ABの中点Mの軌跡を求めよ。
福田の数学〜慶應義塾大学2021年看護医療学部第1問(6)〜高次方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (6)$a,b$を実数、$i$を虚数単位とする。4次方程式
$x^4+(a+2)x^3-(2a+2)x^2+(b+1)x+a^3=0$
の1つの解が$1+i$であるとき、
$a=\boxed{\ \ コ\ \ }, b=\boxed{\ \ サ\ \ }$
である。また、他の解は$\boxed{\ \ シ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{1}}$ (6)$a,b$を実数、$i$を虚数単位とする。4次方程式
$x^4+(a+2)x^3-(2a+2)x^2+(b+1)x+a^3=0$
の1つの解が$1+i$であるとき、
$a=\boxed{\ \ コ\ \ }, b=\boxed{\ \ サ\ \ }$
である。また、他の解は$\boxed{\ \ シ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
福田のわかった数学〜高校3年生理系059〜微分(4)陰関数の微分

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(4) 陰関数の微分
$\frac{x^2}{4}-\frac{y^2}{9}=1$について$\frac{dy}{dx},\frac{d^2y}{dx^2}$を
$x$と$y$を用いて表せ。ただし、$y\neq 0$とする。
この動画を見る
数学$\textrm{III}$ 微分(4) 陰関数の微分
$\frac{x^2}{4}-\frac{y^2}{9}=1$について$\frac{dy}{dx},\frac{d^2y}{dx^2}$を
$x$と$y$を用いて表せ。ただし、$y\neq 0$とする。
福田の数学〜慶應義塾大学2021年看護医療学部第1問(5)〜約数の個数が6個の自然数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (5)自然数nは1とn以外にちょうど4個の約数をもつとする。このような
自然数nの中で、最小の数は$\boxed{\ \ ク\ \ }$であり、最小の奇数は$\boxed{\ \ ケ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{1}}$ (5)自然数nは1とn以外にちょうど4個の約数をもつとする。このような
自然数nの中で、最小の数は$\boxed{\ \ ク\ \ }$であり、最小の奇数は$\boxed{\ \ ケ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
福田のわかった数学〜高校1年生044〜三角形への応用(1)正弦定理の証明

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 三角形への応用(1)
三角形ABCの外接円の半径をRとする。
$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$
が成り立つことを示せ。
この動画を見る
数学$\textrm{I}$ 三角形への応用(1)
三角形ABCの外接円の半径をRとする。
$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$
が成り立つことを示せ。
福田の数学〜慶應義塾大学2021年看護医療学部第1問(4)〜等比数列となる条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (4)数列$\left\{a_n\right\}$の階差数列を$\left\{b_n\right\}$とする。$\left\{b_n\right\}$が初項2、公比$\frac{1}{3}$の等比数列と
なるとき、$\left\{b_n\right\}$の一般項は$b_n=\boxed{\ \ オ\ \ }$である。また、$\left\{a_n\right\}$も等比数列に
なるならば、$a_1=\boxed{\ \ カ\ \ }$である。このとき$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ キ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{1}}$ (4)数列$\left\{a_n\right\}$の階差数列を$\left\{b_n\right\}$とする。$\left\{b_n\right\}$が初項2、公比$\frac{1}{3}$の等比数列と
なるとき、$\left\{b_n\right\}$の一般項は$b_n=\boxed{\ \ オ\ \ }$である。また、$\left\{a_n\right\}$も等比数列に
なるならば、$a_1=\boxed{\ \ カ\ \ }$である。このとき$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ キ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
福田のわかった数学〜高校3年生理系058〜微分(3)媒介変数表示の微分

単元:
#平面上の曲線#微分とその応用#色々な関数の導関数#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数列$\textrm{III}$ 微分(3) 媒介変数表示
$x=a(\theta-\sin\theta), y=a(1-\cos\theta)$のとき、$\frac{dy}{dx},\frac{d^2y}{dx^2}$を$\theta$で表せ。
この動画を見る
数列$\textrm{III}$ 微分(3) 媒介変数表示
$x=a(\theta-\sin\theta), y=a(1-\cos\theta)$のとき、$\frac{dy}{dx},\frac{d^2y}{dx^2}$を$\theta$で表せ。
福田の数学〜慶應義塾大学2021年看護医療学部第1問(3)〜指数法則と式の値

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (3)実数$a$が$2^a-2^{-a}=3$を満たしているとき、$2^a=\boxed{\ \ ウ\ \ }$であり、
$4^a-4^{-a}=\boxed{\ \ エ\ \ }$
である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{1}}$ (3)実数$a$が$2^a-2^{-a}=3$を満たしているとき、$2^a=\boxed{\ \ ウ\ \ }$であり、
$4^a-4^{-a}=\boxed{\ \ エ\ \ }$
である。
2021慶應義塾大学看護医療学部過去問
福田のわかった数学〜高校2年生043〜軌跡(10)中点の軌跡(1)

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 軌跡(10) 中点の軌跡(1)
放物線$y=(x-1)^2\ldots①$と直線$y=mx-3\ldots②$
が異なる2点A,Bで交わるとき、線分ABの中点Mの軌跡を求めよ。
この動画を見る
数学$\textrm{II}$ 軌跡(10) 中点の軌跡(1)
放物線$y=(x-1)^2\ldots①$と直線$y=mx-3\ldots②$
が異なる2点A,Bで交わるとき、線分ABの中点Mの軌跡を求めよ。
福田の数学〜慶應義塾大学2021年看護医療学部第1問(2)〜三角方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#図形と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#三角関数とグラフ#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$
(2)$2(\cos\theta-\sin\theta)^2=1$を満たす$\theta$を$0 \leqq \theta \leqq \pi$の範囲で求めると$\boxed{\ \ イ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{1}}$
(2)$2(\cos\theta-\sin\theta)^2=1$を満たす$\theta$を$0 \leqq \theta \leqq \pi$の範囲で求めると$\boxed{\ \ イ\ \ }$である。
2021慶應義塾大学看護医療学部過去問
福田のわかった数学〜高校3年生理系057〜微分(2)逆関数の微分

単元:
#微分とその応用#微分法#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(2) 逆関数の微分
$y=\tan x (-\frac{\pi}{2} \lt x \lt \frac{\pi}{2})$
の逆関数の第2次導関数を求めよ。
この動画を見る
数学$\textrm{III}$ 微分(2) 逆関数の微分
$y=\tan x (-\frac{\pi}{2} \lt x \lt \frac{\pi}{2})$
の逆関数の第2次導関数を求めよ。
福田の数学〜慶應義塾大学2021年看護医療学部第1問(1)〜二項定理

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)$(a+b)^{21}$の展開式$a^{18}b^3$の係数は$\boxed{\ \ ア\ \ }$である。
$(a+b+c)^{21}$の展開式における$a^{12}b^3c^6$の係数を求めよ。
2021慶應義塾大学看護医療学部過去問
この動画を見る
${\Large\boxed{1}}$(1)$(a+b)^{21}$の展開式$a^{18}b^3$の係数は$\boxed{\ \ ア\ \ }$である。
$(a+b+c)^{21}$の展開式における$a^{12}b^3c^6$の係数を求めよ。
2021慶應義塾大学看護医療学部過去問
福田のわかった数学〜高校1年生043〜三角比の相互関係(2)

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 三角比の相互関係(2)
$\sin\theta+\cos\theta=\frac{\sqrt3-1}{2} (90° \lt \theta \lt 180°)$のとき
$\sin\theta\cos\theta,\sin^3\theta+\cos^3\theta,\sin\theta-\cos\theta,$
$\tan\theta+\frac{1}{\tan\theta},\tan^2\theta+\frac{1}{\tan^2\theta}$の値を求めよ。
この動画を見る
数学$\textrm{I}$ 三角比の相互関係(2)
$\sin\theta+\cos\theta=\frac{\sqrt3-1}{2} (90° \lt \theta \lt 180°)$のとき
$\sin\theta\cos\theta,\sin^3\theta+\cos^3\theta,\sin\theta-\cos\theta,$
$\tan\theta+\frac{1}{\tan\theta},\tan^2\theta+\frac{1}{\tan^2\theta}$の値を求めよ。
福田の数学〜慶應義塾大学2021年薬学部第3問〜3次関数と接線

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$xy平面上に、xの関数
$f(x)=x^3+(a+4)x^2+(4a+6)x+4a+2$
のグラフ$y=f(x)$がある。$y=f(x)$が任意のaに対して
通る定点をP、点Pにおける接線が$y=f(x)$と交わる点をQとおく。
(1)点Pの座標は$\boxed{\ \ ツ\ \ }$であり、点Pにおける接線の方程式は$y=\boxed{\ \ テ\ \ }$である。
(2)$a=5$のとき、$y=f(x)$上の点における接線は、$x=\boxed{\ \ ト\ \ }$において傾きが
最小になる。
(3)$x=\boxed{\ \ ト\ \ }$において$f(x)$が極値をとるとき、$a=\boxed{\ \ ナ\ \ }$であり、
点$(\boxed{\ \ ト\ \ },f(\boxed{\ \ ト\ \ }))$を$S$とおくと、三角形SPQの面積は$\boxed{\ \ ニ\ \ }$である。
2021慶應義塾大学薬学部過去問
この動画を見る
${\Large\boxed{3}}$xy平面上に、xの関数
$f(x)=x^3+(a+4)x^2+(4a+6)x+4a+2$
のグラフ$y=f(x)$がある。$y=f(x)$が任意のaに対して
通る定点をP、点Pにおける接線が$y=f(x)$と交わる点をQとおく。
(1)点Pの座標は$\boxed{\ \ ツ\ \ }$であり、点Pにおける接線の方程式は$y=\boxed{\ \ テ\ \ }$である。
(2)$a=5$のとき、$y=f(x)$上の点における接線は、$x=\boxed{\ \ ト\ \ }$において傾きが
最小になる。
(3)$x=\boxed{\ \ ト\ \ }$において$f(x)$が極値をとるとき、$a=\boxed{\ \ ナ\ \ }$であり、
点$(\boxed{\ \ ト\ \ },f(\boxed{\ \ ト\ \ }))$を$S$とおくと、三角形SPQの面積は$\boxed{\ \ ニ\ \ }$である。
2021慶應義塾大学薬学部過去問
福田のわかった数学〜高校3年生理系056〜微分(1)逆関数の微分

単元:
#微分とその応用#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 微分(1) 逆関数の微分
$y=\sin x (-\frac{\pi}{2} \lt x \lt \frac{\pi}{2})$
の逆関数の導関数を求めよ。
この動画を見る
数学$\textrm{III}$ 微分(1) 逆関数の微分
$y=\sin x (-\frac{\pi}{2} \lt x \lt \frac{\pi}{2})$
の逆関数の導関数を求めよ。
福田の数学〜慶應義塾大学2021年薬学部第2問〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large{\boxed{2}}}$与えられた図形の頂点から無作為に異なる3点を選んで三角形を作る試行を考える。ただし、
この試行におけるすべての根元事象は同様に確からしいとする。
(1)正n角形における前事象を$U_n$とし、その中で面積が最小の三角形ができる
事象を$A_n$とする。ただし、$n$は$n \geqq 6$を満たす自然数とする。
$(\textrm{i})$事象$U_6$において、事象$A_6$の確率は$\boxed{\ \ ス\ \ }$である。
$(\textrm{ii})$事象$U_n$において、事象$A_n$の確率をnの式で表すと$\boxed{\ \ セ\ \ }$であり、
この確率が$\frac{1}{1070}$以下になる最小の$n$の値は$\boxed{\ \ ソ\ \ }$である。
$(\textrm{iii})$事象$U_n \cap \bar{ A_n }$において、面積が最小となる三角形ができる確率をnの式で
表すと$\boxed{\ \ タ\ \ }$である。
(2)1辺の長さが$\sqrt2$である立方体における全事象をVとすると、事象$V$に含まれ
るすべての三角形の面積の平均値は$\boxed{\ \ チ\ \ }$である。
2021慶應義塾大学薬学部過去問
この動画を見る
${\Large{\boxed{2}}}$与えられた図形の頂点から無作為に異なる3点を選んで三角形を作る試行を考える。ただし、
この試行におけるすべての根元事象は同様に確からしいとする。
(1)正n角形における前事象を$U_n$とし、その中で面積が最小の三角形ができる
事象を$A_n$とする。ただし、$n$は$n \geqq 6$を満たす自然数とする。
$(\textrm{i})$事象$U_6$において、事象$A_6$の確率は$\boxed{\ \ ス\ \ }$である。
$(\textrm{ii})$事象$U_n$において、事象$A_n$の確率をnの式で表すと$\boxed{\ \ セ\ \ }$であり、
この確率が$\frac{1}{1070}$以下になる最小の$n$の値は$\boxed{\ \ ソ\ \ }$である。
$(\textrm{iii})$事象$U_n \cap \bar{ A_n }$において、面積が最小となる三角形ができる確率をnの式で
表すと$\boxed{\ \ タ\ \ }$である。
(2)1辺の長さが$\sqrt2$である立方体における全事象をVとすると、事象$V$に含まれ
るすべての三角形の面積の平均値は$\boxed{\ \ チ\ \ }$である。
2021慶應義塾大学薬学部過去問
福田のわかった数学〜高校2年生042〜軌跡(9)媒介変数表示の軌跡(2)

単元:
#数Ⅱ#平面上の曲線#図形と方程式#軌跡と領域#媒介変数表示と極座標#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 軌跡(9) 媒介変数表示(2)
tが実数値をとって変化するとき、
$x=\frac{t^2-1}{t^2+1} y=\frac{2t}{t^2+1}$
はどんな曲線を表すか。
この動画を見る
数学$\textrm{II}$ 軌跡(9) 媒介変数表示(2)
tが実数値をとって変化するとき、
$x=\frac{t^2-1}{t^2+1} y=\frac{2t}{t^2+1}$
はどんな曲線を表すか。
福田の数学〜慶應義塾大学2021年薬学部第1問(7)〜四面体の体積

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ (7)座標空間内に4点$A(0,-2,2),\ B(0,2,2),\ C(2,0,-2),\ D(-2,0,-2)$がある。
この4点を頂点とする四面体ABCDの体積は$\boxed{シ}$である。
2021慶應義塾大学薬学部過去問
この動画を見る
${\Large\boxed{1}}$ (7)座標空間内に4点$A(0,-2,2),\ B(0,2,2),\ C(2,0,-2),\ D(-2,0,-2)$がある。
この4点を頂点とする四面体ABCDの体積は$\boxed{シ}$である。
2021慶應義塾大学薬学部過去問
福田のわかった数学〜高校3年生理系055〜格子点の個数と極限
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
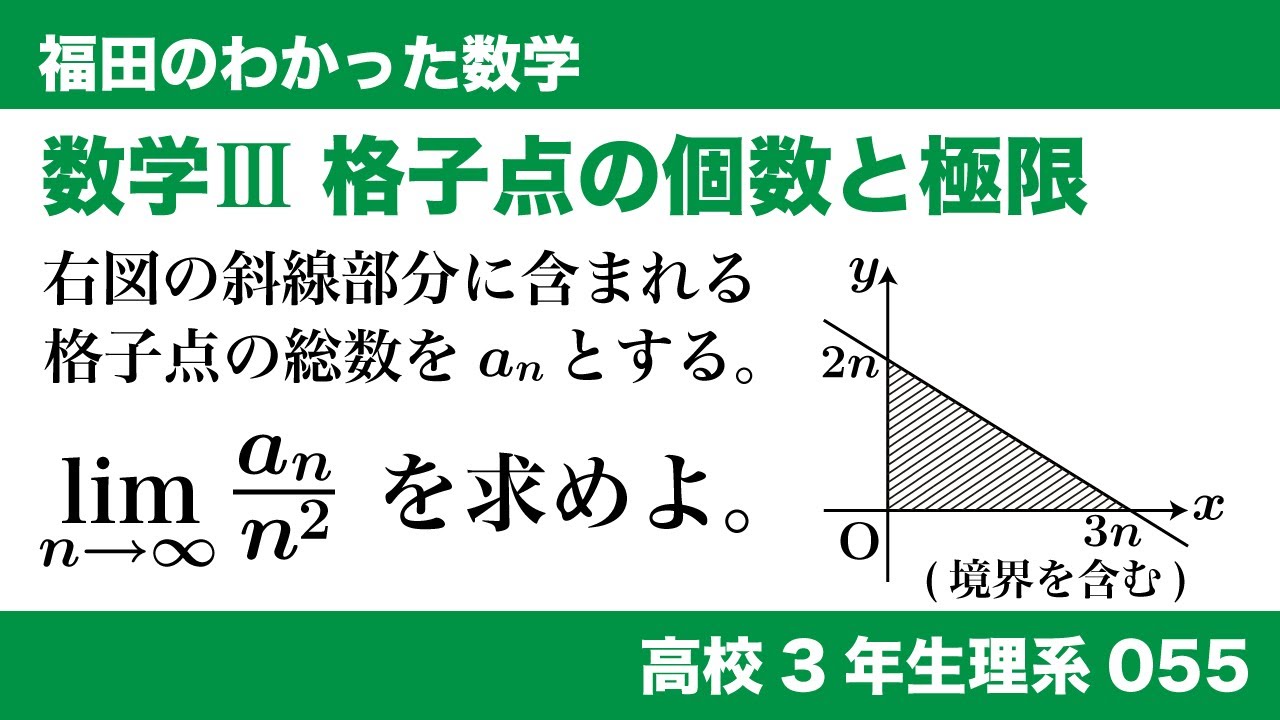
数学$\textrm{III}$ 格子点の個数と極限
右図の斜線部分(※動画参照)に含まれる
格子点の総数を$a_n$とする。
$\lim_{n \to \infty}\frac{a_n}{n^2}$を求めよ。
この動画を見る
数学$\textrm{III}$ 格子点の個数と極限
右図の斜線部分(※動画参照)に含まれる
格子点の総数を$a_n$とする。
$\lim_{n \to \infty}\frac{a_n}{n^2}$を求めよ。
福田の数学〜慶應義塾大学2021年薬学部第1問(6)〜整数解

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(6)整数$x,y$が$x \gt 1,y \gt 1,x \neq y$を満たし、等式
$6x^2+13xy+7x+5y^2+7y+2=966$
を満たすとする。
$(\textrm{i})6x^2+13xy+7x+5y^2+7y+2$を因数分解すると$\boxed{\ \ コ\ \ }$である。
$(\textrm{ii})$この等式を満たすxとyの組をすべて挙げると$(x,y)=\boxed{\ \ サ\ \ }$である。
2021慶應義塾大学薬学部過去問
この動画を見る
${\Large\boxed{1}}$(6)整数$x,y$が$x \gt 1,y \gt 1,x \neq y$を満たし、等式
$6x^2+13xy+7x+5y^2+7y+2=966$
を満たすとする。
$(\textrm{i})6x^2+13xy+7x+5y^2+7y+2$を因数分解すると$\boxed{\ \ コ\ \ }$である。
$(\textrm{ii})$この等式を満たすxとyの組をすべて挙げると$(x,y)=\boxed{\ \ サ\ \ }$である。
2021慶應義塾大学薬学部過去問



