ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
大学入試問題#689「簡単にさばきたい」 埼玉医科大学(2007) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} (1+\sqrt{ 1-x^2 })^2 dx$
出典：2007年埼玉医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} (1+\sqrt{ 1-x^2 })^2 dx$
出典：2007年埼玉医科大学 入試問題
大学入試問題#688「怖いのはミス」 東京女子医科大学(2015) 定積分
単元：
#大学入試過去問(数学)#数学(高校生)#東京女子医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\log\ 2} \displaystyle \frac{e^{5x}}{e^x+1} dx$
出典：2015年東京女子医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\log\ 2} \displaystyle \frac{e^{5x}}{e^x+1} dx$
出典：2015年東京女子医科大学 入試問題
大学入試問題#687「なんか見える」 東海大学医学部(2014)
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師：
ますただ
問題文全文(内容文)：
$a \gt 0$のとき、
$a+\displaystyle \frac{17}{a+4}$の最小値を求めよ
出典：2014年東海大学医学部 入試問題
この動画を見る
$a \gt 0$のとき、
$a+\displaystyle \frac{17}{a+4}$の最小値を求めよ
出典：2014年東海大学医学部 入試問題
大学入試問題#686「簡単ですみません。」 富山大学(2023) 計算問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学
指導講師：
ますただ
問題文全文(内容文)：
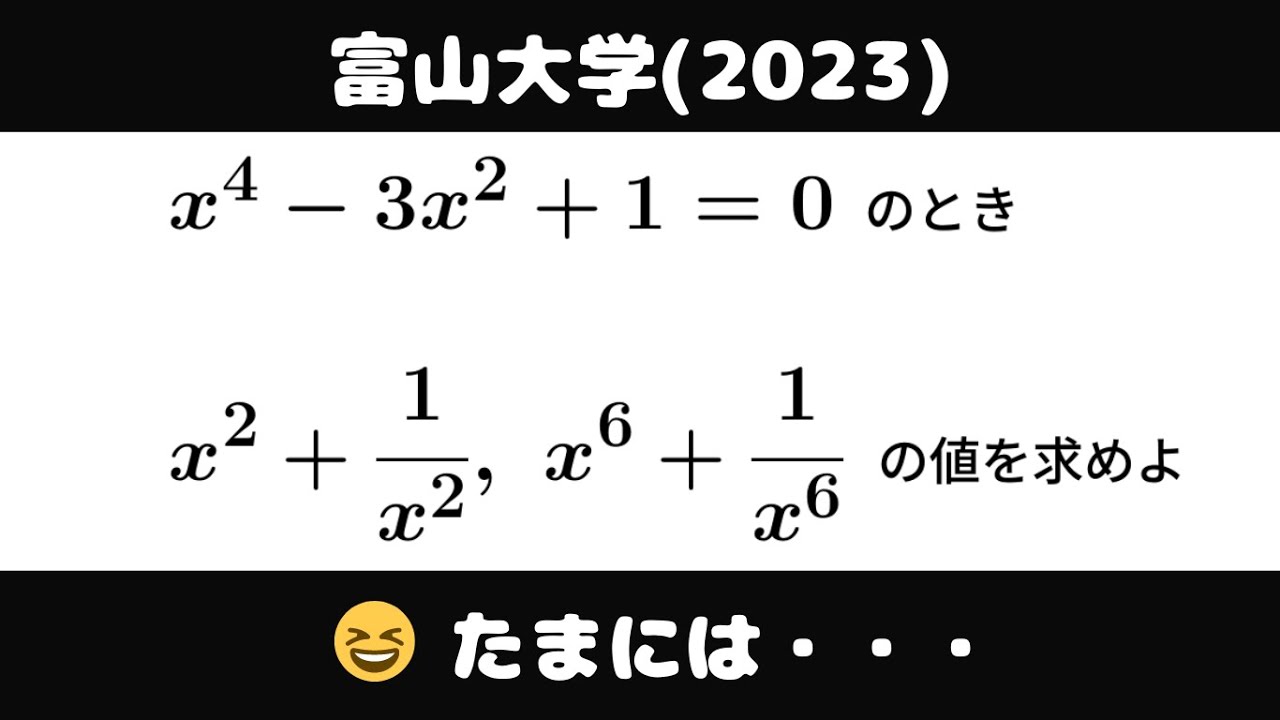
$x^4-3x^2+1=0$のとき
$x^2+\displaystyle \frac{1}{x^2},x^6+\displaystyle \frac{1}{x^6}$の値を求めよ
出典：2023年富山大学 入試問題
この動画を見る
$x^4-3x^2+1=0$のとき
$x^2+\displaystyle \frac{1}{x^2},x^6+\displaystyle \frac{1}{x^6}$の値を求めよ
出典：2023年富山大学 入試問題
大学入試問題#687「至高の積分」 富山大学(2023) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学
指導講師：
ますただ
問題文全文(内容文)：
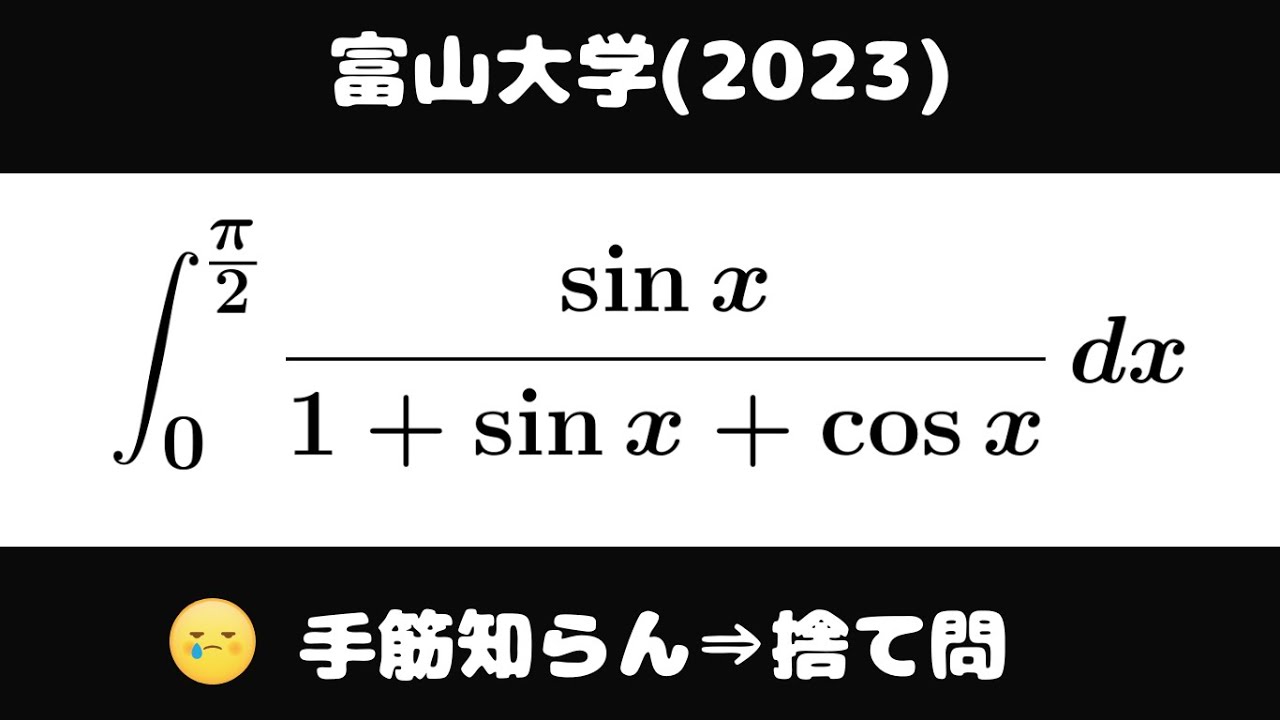
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x}{1+\sin\ x+\cos\ x} dx$
出典：2023年富山大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x}{1+\sin\ x+\cos\ x} dx$
出典：2023年富山大学 入試問題
大学入試問題#685「一言・・・むずい」 早稲田商学部(2018) #整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
次の条件を満たす正の整数の組$(a,b,n)$をすべて求めよ。
$n \geq 2$で、$b$は素数
$a^2=b^n+225$
出典：2018年早稲田大学商学部 入試問題
この動画を見る
次の条件を満たす正の整数の組$(a,b,n)$をすべて求めよ。
$n \geq 2$で、$b$は素数
$a^2=b^n+225$
出典：2018年早稲田大学商学部 入試問題
大学入試問題#684「沼にはまると抜けれない」 早稲田商学部(1999) #三角関数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\sin\ x+\sin\ y=1$
$\cos\ x+\cos\ y=\displaystyle \frac{1}{3}$
のとき、$\tan\displaystyle \frac{x+y}{2}$の値を求めよ
出典：1999年早稲田大学商学部 入試問題
この動画を見る
$\sin\ x+\sin\ y=1$
$\cos\ x+\cos\ y=\displaystyle \frac{1}{3}$
のとき、$\tan\displaystyle \frac{x+y}{2}$の値を求めよ
出典：1999年早稲田大学商学部 入試問題
大学入試問題#683「早稲田大学人間科学部(2014)と同型」 昭和大学医学部(2023)
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
実数$a,b,c$が
$a+b+c=8$
$a^2+b^2+c^2=32$
を満たすとき、$c$の値が取りうる範囲を求めよ。
出典：2023年昭和大学医学部 入試問題
この動画を見る
実数$a,b,c$が
$a+b+c=8$
$a^2+b^2+c^2=32$
を満たすとき、$c$の値が取りうる範囲を求めよ。
出典：2023年昭和大学医学部 入試問題
大学入試問題#682「もはや、言うまでもない」 富山大学(2023) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{1+2\sin\ x}{1+\sin\ x+\cos\ x} dx$
出典：2023年富山大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{1+2\sin\ x}{1+\sin\ x+\cos\ x} dx$
出典：2023年富山大学 入試問題
大学入試問題#681「綺麗な良問」 東京理科大学(2016) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{4}} \displaystyle \frac{\sin\ 4x}{\sqrt{ 1+\sin^2x }} dx$
出典：2016年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}} \displaystyle \frac{\sin\ 4x}{\sqrt{ 1+\sin^2x }} dx$
出典：2016年東京理科大学 入試問題
大学入試問題#680「よく見る形」 東京理科大学(2015) 極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \infty } (\displaystyle \frac{x+3}{x-3})^x$
出典：2015年東京理科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to \infty } (\displaystyle \frac{x+3}{x-3})^x$
出典：2015年東京理科大学 入試問題
大学入試問題#679「基本的な極限問題」 愛知医科大学(2020) 極限
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#愛知医科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{2^x-1}{\sin\ 2x}$
出典：2020年愛知医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{2^x-1}{\sin\ 2x}$
出典：2020年愛知医科大学 入試問題
大学入試問題#678「基本問題」 東京理科大学(2016) 不定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x^3}{\sqrt{ 2x^2+3 }} dx$
出典：2016年東京理科大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x^3}{\sqrt{ 2x^2+3 }} dx$
出典：2016年東京理科大学 入試問題
大学入試問題#677「よく見る形となんか違う」 東京女子医科大学(2017) #整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京女子医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \frac{n^2}{m}+\displaystyle \frac{m}{n}=8$を満たす自然数の組$(m,n)$をすべて求めよ
出典：2017年東京女子医科大学 入試問題
この動画を見る
$\displaystyle \frac{n^2}{m}+\displaystyle \frac{m}{n}=8$を満たす自然数の組$(m,n)$をすべて求めよ
出典：2017年東京女子医科大学 入試問題
「綺麗な定積分」 2021年大阪教員採用試験
単元：
#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2} \displaystyle \frac{x^2+x+1}{x^3+1} dx$
出典：2021年大阪府教員採用試験
この動画を見る
$\displaystyle \int_{0}^{2} \displaystyle \frac{x^2+x+1}{x^3+1} dx$
出典：2021年大阪府教員採用試験
大学入試問題#676「たぶん良い問題」 東京理科大学(2017) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} \displaystyle \frac{4x+1}{x^4+2x^3+x+2}dx$
出典：2017年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{4x+1}{x^4+2x^3+x+2}dx$
出典：2017年東京理科大学 入試問題
鬼の定積分「投了・・・」 By 英語orドイツ語シはBかHか さん
単元：
#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}} log (\displaystyle \frac{\sin\ x+\cos\ x+1}{\sin\ 2x+1}) dx$
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} log (\displaystyle \frac{\sin\ x+\cos\ x+1}{\sin\ 2x+1}) dx$
大学入試問題#675「y軸回転はバームクーヘンから考えたくなる」久留米大学医学部(2010)
単元：
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#久留米大学
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=2x\sqrt{ 2-x^2 }$
$y=f(x)$のグラフと$x$軸とで囲まれる図形を$y$軸の周りに回転させてできる立体の体積を求めよ
出典：2010年久留米大学医学部 入試問題
この動画を見る
$f(x)=2x\sqrt{ 2-x^2 }$
$y=f(x)$のグラフと$x$軸とで囲まれる図形を$y$軸の周りに回転させてできる立体の体積を求めよ
出典：2010年久留米大学医学部 入試問題
大学入試問題#674「もう飽きてきました」日本大学医学部(2006)
単元：
#大学入試過去問(数学)#定積分#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{x\ \sin\ x}{3+\sin^2\ x} dx$
出典：2006年日本大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{x\ \sin\ x}{3+\sin^2\ x} dx$
出典：2006年日本大学医学部 入試問題
大学入試問題#673「何度も解いてるはず」 東京慈恵会医科大学(2001)
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学#東京慈恵会医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} log(x^2+3) dx$
出典：2001年東京慈恵会医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} log(x^2+3) dx$
出典：2001年東京慈恵会医科大学 入試問題
大学入試問題#672「最近、このタイプが流行り？」 早稲田大学商学部(2022)
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
実数$x,y$が$x^2+y^2 \leqq 3$を満たしているとき$x-y-xy$の最大値を求めよ
出典：2022年早稲田大学商学部 入試問題
この動画を見る
実数$x,y$が$x^2+y^2 \leqq 3$を満たしているとき$x-y-xy$の最大値を求めよ
出典：2022年早稲田大学商学部 入試問題
大学入試問題#671「方針が見えやすい良問」 東京医科大学(2001)
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科大学#東京医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{\frac{3}{2}} \displaystyle \frac{x^2}{\sqrt{ 2x-x^2 }} dx$
出典：2001年東京医科大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{\frac{3}{2}} \displaystyle \frac{x^2}{\sqrt{ 2x-x^2 }} dx$
出典：2001年東京医科大学 入試問題
大学入試問題#670「これ気づきますよね」 愛知工業大学(2023) 三角関数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#愛知工業大学
指導講師：
ますただ
問題文全文(内容文)：
$-\displaystyle \frac{\pi}{4} \leqq x \leqq \displaystyle \frac{\pi}{4}$
$\displaystyle \frac{1+\sqrt{ 3 }\tan\ x}{\sqrt{ 3 }-\tan\ x}$の最大値と最小値を求めよ
出典：2023年愛知工業大学 入試問題
この動画を見る
$-\displaystyle \frac{\pi}{4} \leqq x \leqq \displaystyle \frac{\pi}{4}$
$\displaystyle \frac{1+\sqrt{ 3 }\tan\ x}{\sqrt{ 3 }-\tan\ x}$の最大値と最小値を求めよ
出典：2023年愛知工業大学 入試問題
大学入試問題#669「標準運転」 東京女子医科大学(2002) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京女子医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e} \displaystyle \frac{(log\ x)^2}{x^3} dx$
出典：2002年東京女子医科大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e} \displaystyle \frac{(log\ x)^2}{x^3} dx$
出典：2002年東京女子医科大学 入試問題
ハウスドルフ空間の基本性質
大学入試問題#668「解き方は色々あると思います」 埼玉医科大学(2007)定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{dx}{1+\sqrt{ 3 }\tan\ x}$
出典：2007年埼玉医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{dx}{1+\sqrt{ 3 }\tan\ x}$
出典：2007年埼玉医科大学 入試問題
大学入試問題#667「いつの時代もお目にかかる」 昭和大学医学部(2008) 積分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#昭和大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{a}^{2-x} f(t) dt=x^2$を満たす関数$f(x)$と定数$a$の値を求めよ
出典：2008年昭和大学医学部 入試問題
この動画を見る
$\displaystyle \int_{a}^{2-x} f(t) dt=x^2$を満たす関数$f(x)$と定数$a$の値を求めよ
出典：2008年昭和大学医学部 入試問題
大学入試問題#666「受験生には是非解いてほしい良問」 京都大学(1969)
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
実数$x,y$が次の範囲を動くものとする。
$x \geqq 0,\ y \geqq 0,\ x+y \geqq 1$
$a$が正の定数であるとき
$f(x,y)=\sqrt{ x }+a\sqrt{ y }$の最小値を求めよ
出典：1969年京都大学 入試問題
この動画を見る
実数$x,y$が次の範囲を動くものとする。
$x \geqq 0,\ y \geqq 0,\ x+y \geqq 1$
$a$が正の定数であるとき
$f(x,y)=\sqrt{ x }+a\sqrt{ y }$の最小値を求めよ
出典：1969年京都大学 入試問題
大学入試問題#665「直線的な解答は厳禁」 藤田医科大学(2023) 2024年入学の問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
$a,b,x,y$：実数
$a^2+b^2=49$
$x^2+y^2=36$のとき
$ax+by$の最大値を求めよ。
出典：2023年藤田歯科大学 入試問題
この動画を見る
$a,b,x,y$：実数
$a^2+b^2=49$
$x^2+y^2=36$のとき
$ax+by$の最大値を求めよ。
出典：2023年藤田歯科大学 入試問題
この積分は解けませんでした。 By Picmin3daisukiさん
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
（1）
$I=\displaystyle \int_{1}^{2} 2^{2^x} dx$のとき
$\displaystyle \int_{1}^{2} 2^{2x}log(2x)dx$を$I$を用いて表せ
（2）
$I=\displaystyle \int_{1}^{2} (2^{2^x}+2^{(2x+1)}log\ x) dx$を求めよ
この動画を見る
（1）
$I=\displaystyle \int_{1}^{2} 2^{2^x} dx$のとき
$\displaystyle \int_{1}^{2} 2^{2x}log(2x)dx$を$I$を用いて表せ
（2）
$I=\displaystyle \int_{1}^{2} (2^{2^x}+2^{(2x+1)}log\ x) dx$を求めよ