ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
大学入試問題#105 京都大学(2003) 数列
単元：
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師：
ますただ
問題文全文(内容文)：
$a_n \gt 0,\ a_1=1$
$n \geqq 2$のとき
$log\ a_n-log\ a_{n-1}=log(n-1)-log(n+1)$である。
$\displaystyle \sum_{k=1}^n a_k$を求めよ
出典：2003年京都大学 入試問題
この動画を見る
$a_n \gt 0,\ a_1=1$
$n \geqq 2$のとき
$log\ a_n-log\ a_{n-1}=log(n-1)-log(n+1)$である。
$\displaystyle \sum_{k=1}^n a_k$を求めよ
出典：2003年京都大学 入試問題
大学入試問題#104 一橋大学(2006) ベクトル
単元：
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$|\vec{ a }|=5,|\vec{ b }|=3,|\vec{ c }|=1$
$\vec{ Z }=\vec{ a }+\vec{ b }+\vec{ c }$
（1）$|\vec{ Z }|$の最大値、最小値
（2）$\vec{ a }・\vec{ Z }=20$
をみたすとき
$|\vec{ Z }|$の最大値、最小値を求めよ
出典：2006年一橋大学 入試問題
この動画を見る
$|\vec{ a }|=5,|\vec{ b }|=3,|\vec{ c }|=1$
$\vec{ Z }=\vec{ a }+\vec{ b }+\vec{ c }$
（1）$|\vec{ Z }|$の最大値、最小値
（2）$\vec{ a }・\vec{ Z }=20$
をみたすとき
$|\vec{ Z }|$の最大値、最小値を求めよ
出典：2006年一橋大学 入試問題
大学入試問題#103 東海大学医学部(2017) 二項定理
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師：
ますただ
問題文全文(内容文)：
次の和を求めよ。
（1）
${}_{ n }C_0+{}_{ n }C_1+・・・+{}_{ n }C_n$
（2）
$\displaystyle \frac{1}{1!(2n)!}+\displaystyle \frac{1}{2(2n-1)!}+・・・+\displaystyle \frac{1}{n!(n+1)!}$
出典：2017年東海大学医学部 入試問題
この動画を見る
次の和を求めよ。
（1）
${}_{ n }C_0+{}_{ n }C_1+・・・+{}_{ n }C_n$
（2）
$\displaystyle \frac{1}{1!(2n)!}+\displaystyle \frac{1}{2(2n-1)!}+・・・+\displaystyle \frac{1}{n!(n+1)!}$
出典：2017年東海大学医学部 入試問題
大学入試問題#102 高知女子大学(1988) 無限級数
単元：
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \sum_{n=2}^\infty log(1+\displaystyle \frac{1}{n^2-1})$を求めよ。
出典：1988年高知女子大学 入試問題
この動画を見る
$\displaystyle \sum_{n=2}^\infty log(1+\displaystyle \frac{1}{n^2-1})$を求めよ。
出典：1988年高知女子大学 入試問題
大学入試問題#101 東海大学医学部(2017) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東海大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}x^3(1-x^2)^8dx$を計算せよ。
出典：2017年東海大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}x^3(1-x^2)^8dx$を計算せよ。
出典：2017年東海大学医学部 入試問題
大学入試問題#100 東京大学(1954) 軌跡・領域
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
点（$x,y$）が原点を中心とする半径1の円の内部を動くとき
点（$x+y,xy$）の動く範囲を図示せよ。
出典：1954年東京大学 入試問題
この動画を見る
点（$x,y$）が原点を中心とする半径1の円の内部を動くとき
点（$x+y,xy$）の動く範囲を図示せよ。
出典：1954年東京大学 入試問題
大学入試問題#99 慶應義塾大学2004 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^2+y^2 \lt 9$
$x^2 \leqq y^2$をみたす整数の組$x,y$の個数を求めよ。
出典：2004年慶應義塾大学 入試問題
この動画を見る
$x^2+y^2 \lt 9$
$x^2 \leqq y^2$をみたす整数の組$x,y$の個数を求めよ。
出典：2004年慶應義塾大学 入試問題
大学入試問題#98 千葉大学医学部(2018) 積分・極限
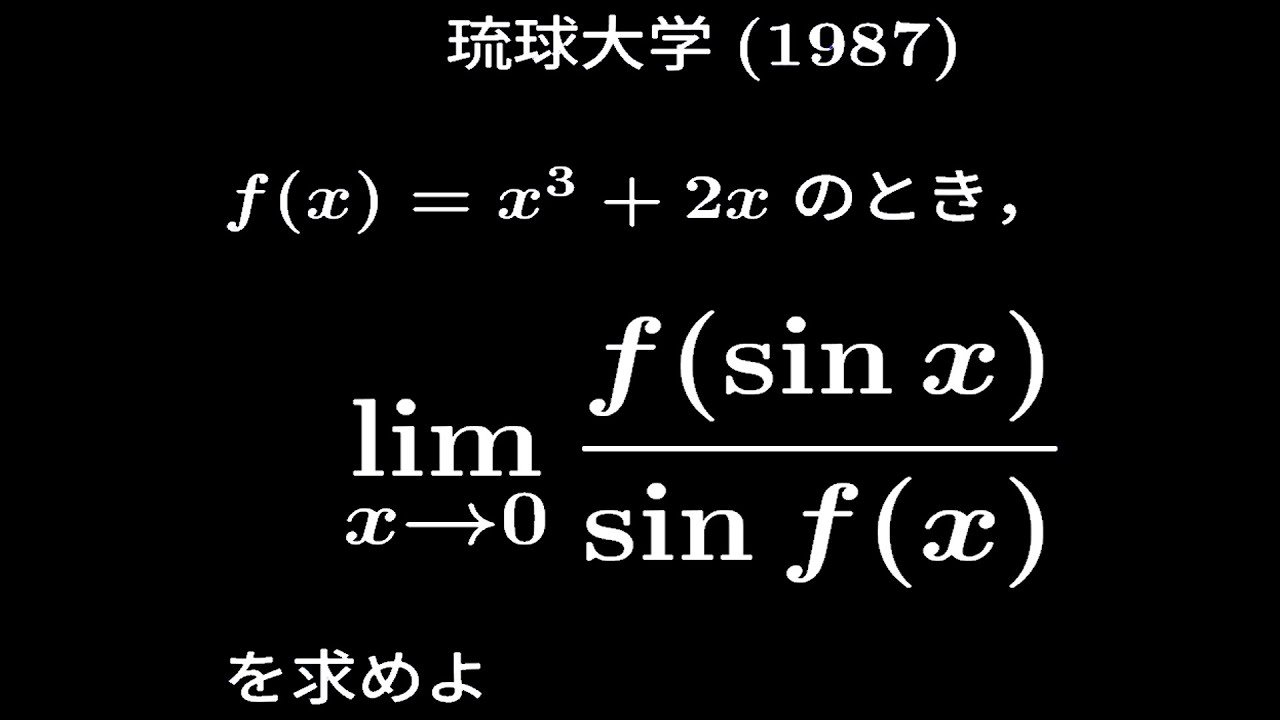
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#不定積分#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
（1）
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$を求めよ。
（2）
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典：2018年千葉大学 入試問題
この動画を見る
（1）
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$を求めよ。
（2）
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典：2018年千葉大学 入試問題
大学入試問題#97 学習院大学(2003) 整数問題 帰納法
単元：
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#数B#学習院大学
指導講師：
ますただ
問題文全文(内容文)：
$n$：自然数
$11^{n+1}+12^{2n-1}$は$19$で割り切れることを示せ
出典：2003年学習院大学 入試問題
この動画を見る
$n$：自然数
$11^{n+1}+12^{2n-1}$は$19$で割り切れることを示せ
出典：2003年学習院大学 入試問題
大学入試問題#96 横浜国立大学(2015) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{log\ 3}\displaystyle \frac{dx}{e^x+5e^{-x}-2}$を求めよ。
出典：2015横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{log\ 3}\displaystyle \frac{dx}{e^x+5e^{-x}-2}$を求めよ。
出典：2015横浜国立大学 入試問題
大学入試問題#95 横浜市立大学医学部(2013) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#横浜市立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sqrt{ 2 }}{\sin\ x+\cos\ x}\ dx$を求めよ。
出典：2013年横浜市立大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sqrt{ 2 }}{\sin\ x+\cos\ x}\ dx$を求めよ。
出典：2013年横浜市立大学医学部 入試問題
大学入試問題#94 横浜国立大学(2007) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{dx}{1+\sin\ x}$を計算せよ。
出典：2007年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{dx}{1+\sin\ x}$を計算せよ。
出典：2007年横浜国立大学 入試問題
大学入試問題#93 昭和大学医学部(2016) 対数
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)#昭和大学
指導講師：
ますただ
問題文全文(内容文)：
$log_xy=log_yx=-log_3(x+y)$をみたす実数$x,y$を求めよ。
出典：2016年昭和大学医学部 入試問題
この動画を見る
$log_xy=log_yx=-log_3(x+y)$をみたす実数$x,y$を求めよ。
出典：2016年昭和大学医学部 入試問題
大学入試問題#92 東京医科大学(2015) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}(x\sqrt{ 1-x^2 })^3 dx$を計算せよ。
出典：2015年東京医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}(x\sqrt{ 1-x^2 })^3 dx$を計算せよ。
出典：2015年東京医科大学 入試問題
大学入試問題#91 関西学院大学(2006) 不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{\sin\ x\ \cos\ x}{2+\cos\ x}\ dx$を計算せよ。
出典：2006年関西学院大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\sin\ x\ \cos\ x}{2+\cos\ x}\ dx$を計算せよ。
出典：2006年関西学院大学 入試問題
大学入試問題#90 京都大学(2001) 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x,y,z$：正の整数
$x^2+2y^2+2z^2-2xy-2xz+2yz-5=0$をみたす組（$x,y,z$）をすべて求めよ。
出典：2001年京都大学 入試問題
この動画を見る
$x,y,z$：正の整数
$x^2+2y^2+2z^2-2xy-2xz+2yz-5=0$をみたす組（$x,y,z$）をすべて求めよ。
出典：2001年京都大学 入試問題
大学入試問題#89 信州大学(1988) 不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int (x^2+a^2)^{-\frac{3}{2}}dx$
$a \neq 0$を計算せよ。
出典：1988年信州大学 入試問題
この動画を見る
$\displaystyle \int (x^2+a^2)^{-\frac{3}{2}}dx$
$a \neq 0$を計算せよ。
出典：1988年信州大学 入試問題
数学ゴールデン【漫画】で紹介された数オリの問題の解答がなかったから作成してみた。
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#式の計算（整式・展開・因数分解）#数学オリンピック#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$0 \lt x$：実数
$x+\sqrt{ x(x+1) }+\sqrt{ x(x+2) }+\sqrt{ (x+1)(x+2) }=2$を解け。
出典：数学ゴールデン 数学オリンピック
この動画を見る
$0 \lt x$：実数
$x+\sqrt{ x(x+1) }+\sqrt{ x(x+2) }+\sqrt{ (x+1)(x+2) }=2$を解け。
出典：数学ゴールデン 数学オリンピック
大学入試問題#88 関西大学(2006) 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$x^3+x^2-1=y(x-1)$をみたす整数の組$(x,y)$をすべて求めよ。
出典：2006年関西大学 入試問題
この動画を見る
$x^3+x^2-1=y(x-1)$をみたす整数の組$(x,y)$をすべて求めよ。
出典：2006年関西大学 入試問題
大学入試問題#87 立命館大学(2018) 整数問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#立命館大学
指導講師：
ますただ
問題文全文(内容文)：
$n$：整数
$\sqrt{ n^2-8n+1 }$が整数となる$n$をすべて求めよ。
出典：2018年立命館大学 入試問題
この動画を見る
$n$：整数
$\sqrt{ n^2-8n+1 }$が整数となる$n$をすべて求めよ。
出典：2018年立命館大学 入試問題
【数学科の学生用】tan x (π/2 ＜ x ＜ π/2)が連続であることをε-δ論法で証明せよ．
単元：
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 269
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 270
Warning: usort() expects parameter 1 to be array, bool given in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 269
Warning: Invalid argument supplied for foreach() in /home/kaiketsudb/kaiketsu-db.net/public_html/wp-content/themes/lightning-child-sample/taxonomy-teacher.php on line 270
指導講師：
ますただ
問題文全文(内容文)：
$f:(-\displaystyle \frac{\pi}{2},\displaystyle \frac{\pi}{2})→\mathbb{ R }$を$f(x)=\tan\ x$で定めると連続であることを示せ
この動画を見る
$f:(-\displaystyle \frac{\pi}{2},\displaystyle \frac{\pi}{2})→\mathbb{ R }$を$f(x)=\tan\ x$で定めると連続であることを示せ
大学入試問題#86 防衛医科大学(1988) 極限
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師：
ますただ
問題文全文(内容文)：
$0 \lt a$：実数
$\displaystyle \lim_{ n \to \infty }(a^n+(1+a)^n)^{\frac{1}{n}}$を求めよ。
出典：1988年防衛医科大学 入試問題
この動画を見る
$0 \lt a$：実数
$\displaystyle \lim_{ n \to \infty }(a^n+(1+a)^n)^{\frac{1}{n}}$を求めよ。
出典：1988年防衛医科大学 入試問題
大学入試問題#85 小樽商科大学(1988) 不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#小樽商科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \sin(log\ x)dx$を計算せよ。
出典：1988年小樽商科大学 入試問題
この動画を見る
$\displaystyle \int \sin(log\ x)dx$を計算せよ。
出典：1988年小樽商科大学 入試問題
大学入試問題#84 弘前大学(1986) 不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{1}{e^x+1}\ dx$を計算せよ。
出典：1986年弘前大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{e^x+1}\ dx$を計算せよ。
出典：1986年弘前大学 入試問題
大学入試問題#83 京都大学(2012) 平面ベクトル
単元：
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$\triangle OAB$において
$OA=3,\ OB=2$
$\angle AOB=60^{ \circ }$
$\triangle OAB$の垂心を$H$とする。
$\overrightarrow{ OH }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$で表せ。
出典：2021年京都大学 入試問題
この動画を見る
$\triangle OAB$において
$OA=3,\ OB=2$
$\angle AOB=60^{ \circ }$
$\triangle OAB$の垂心を$H$とする。
$\overrightarrow{ OH }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$で表せ。
出典：2021年京都大学 入試問題
大学入試問題#82 神戸大学(2012) 複雑な置換積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x-\cos\ x}{1+\cos\ x}\ dx$
出典：2012年神戸大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x-\cos\ x}{1+\cos\ x}\ dx$
出典：2012年神戸大学 入試問題
大学入試問題#81 東京大学(2012) ２次方程式【正確な問題文は概要欄】
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x,y$：実数
$2x^2+4xy+3y^2+4x+5y-4=0$を満たすとき、$x$のとりうる最大の値を求めよ。
出典：2012年東京大学 入試問題
この動画を見る
$x,y$：実数
$2x^2+4xy+3y^2+4x+5y-4=0$を満たすとき、$x$のとりうる最大の値を求めよ。
出典：2012年東京大学 入試問題
大学入試問題#80 信州大学(2001) 不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }+1}\ dx$を計算せよ。
出典：2001年信州大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }+1}\ dx$を計算せよ。
出典：2001年信州大学 入試問題
【全ての問題は概要欄】大学入試問題#79 大阪大学(2020 改) 微分
単元：
#大学入試過去問(数学)#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$0 \leqq x$
関数$f(x)=(x+1)^{\frac{1}{x+1}}$の最大値を求めよ。
出典：2020年大阪大学 入試問題
この動画を見る
$0 \leqq x$
関数$f(x)=(x+1)^{\frac{1}{x+1}}$の最大値を求めよ。
出典：2020年大阪大学 入試問題
大学入試問題#78 横浜国立大学(2006) 置換積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{dx}{\sin^2x+3\cos^2x}$を計算せよ。
出典：2006年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{dx}{\sin^2x+3\cos^2x}$を計算せよ。
出典：2006年横浜国立大学 入試問題