ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
大学入試問題#65 同志社大学(2010) 複雑な部分積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#同志社大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}\sqrt{ 4x^2+1 }\ dx$を計算せよ。
出典：2010年同志社大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\sqrt{ 4x^2+1 }\ dx$を計算せよ。
出典：2010年同志社大学 入試問題
大学入試問題#64 早稲田大学(1987) 置換積分
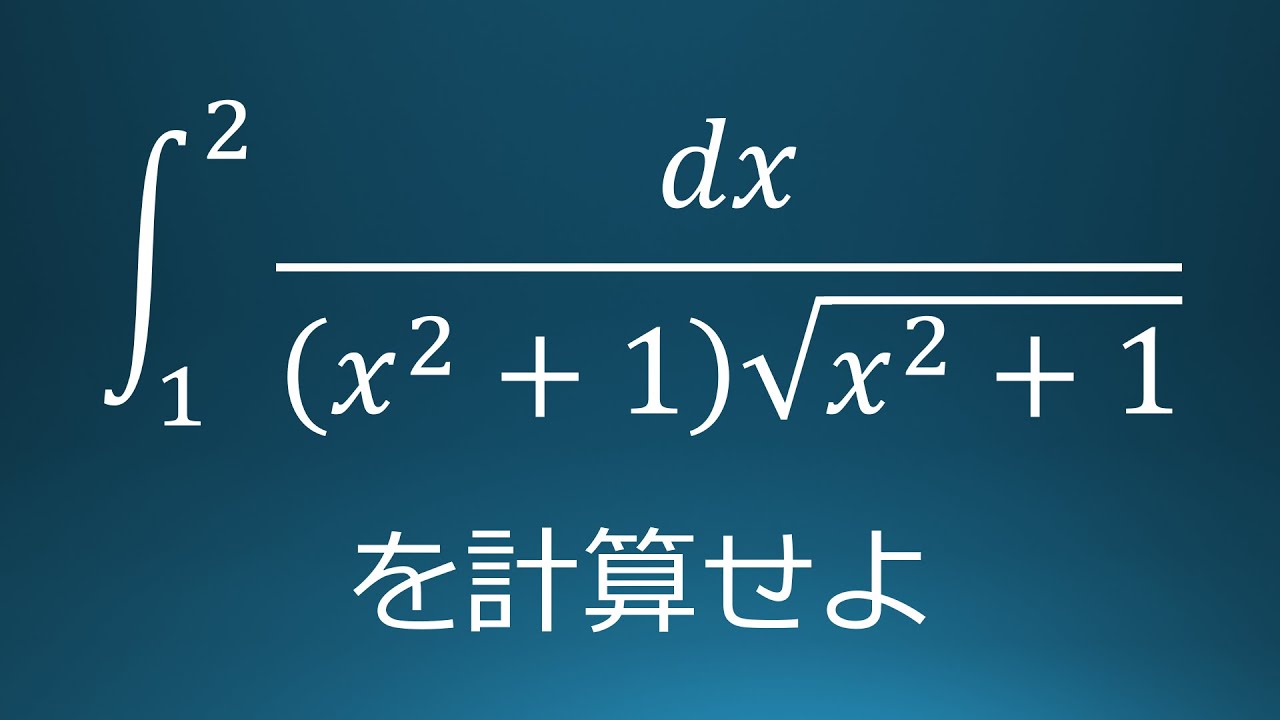
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{2}\displaystyle \frac{dx}{(x^2+1)\sqrt{ x^2+1 }}$を計算せよ。
出典：1987年早稲田大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2}\displaystyle \frac{dx}{(x^2+1)\sqrt{ x^2+1 }}$を計算せよ。
出典：1987年早稲田大学 入試問題
#48 数検1級2次 過去問 整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$m,n$：正の整数
$3^m=n^2-117^2$を満たす$m,n$の値を求めよ。
この動画を見る
$m,n$：正の整数
$3^m=n^2-117^2$を満たす$m,n$の値を求めよ。
大学入試問題#63 京都大学(2011) 気合で置換積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{1}{2}}(x+1)\sqrt{ 1-2x^2 }\ dx$を計算せよ。
出典：2011年京都大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{1}{2}}(x+1)\sqrt{ 1-2x^2 }\ dx$を計算せよ。
出典：2011年京都大学 入試問題
大学入試問題#62 横浜国立大学(2003) 定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e}5^{log\ x}dx$を計算せよ。
出典：2003年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}5^{log\ x}dx$を計算せよ。
出典：2003年横浜国立大学 入試問題
大学入試問題#61 大阪工業大学(2021) 数列
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#大阪工業大学
指導講師：
ますただ
問題文全文(内容文)：
$S_n=\displaystyle \frac{n+3}{2}a_n-6$を満たすとき
一般項$a_n$を求めよ。
出典：2021年大阪工業大学 入試問題
この動画を見る
$S_n=\displaystyle \frac{n+3}{2}a_n-6$を満たすとき
一般項$a_n$を求めよ。
出典：2021年大阪工業大学 入試問題
大学入試問題#60 広島工業大学(2021) 因数定理
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^{2019}+x^{2020}$を$x^2+x+1$で割った余りを求めよ。
出典：2021年広島工業大学 入試問題
この動画を見る
$x^{2019}+x^{2020}$を$x^2+x+1$で割った余りを求めよ。
出典：2021年広島工業大学 入試問題
#47 数検1級1次 過去問 二項定理
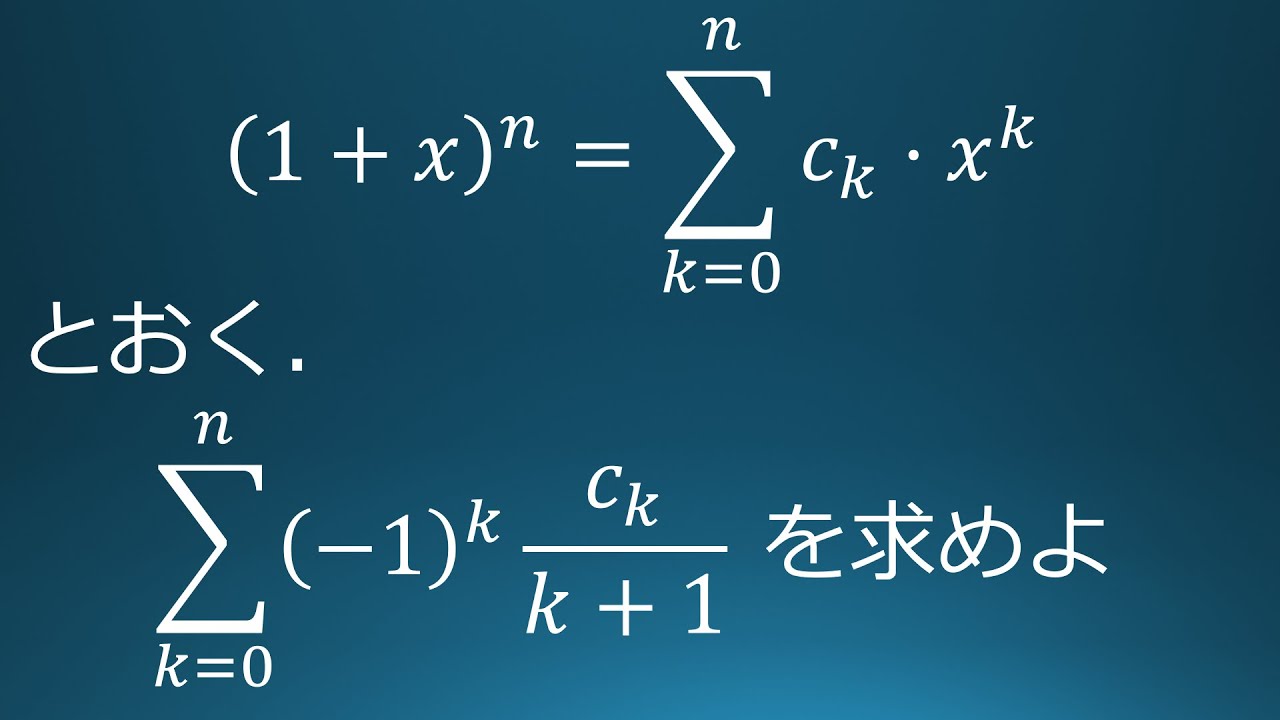
単元：
#数Ⅰ#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#式と証明#微分法と積分法#整式の除法・分数式・二項定理#不定積分・定積分#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$(1+x)^n$を$c_0+c_1x+・・・+c_nx^n$とおく。
$\displaystyle \sum_{k=1}^n(-1)^k\displaystyle \frac{c_k}{k+1}$の値を求めよ。
この動画を見る
$(1+x)^n$を$c_0+c_1x+・・・+c_nx^n$とおく。
$\displaystyle \sum_{k=1}^n(-1)^k\displaystyle \frac{c_k}{k+1}$の値を求めよ。
大学入試問題#59 京都大学(2007) 積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2}\displaystyle \frac{2x+1}{\sqrt{ x^2+4 }}\ dx$を計算せよ。
出典：2007年京都大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2}\displaystyle \frac{2x+1}{\sqrt{ x^2+4 }}\ dx$を計算せよ。
出典：2007年京都大学 入試問題
#46 数検1級1次 過去問 複雑な方程式
単元：
#数Ⅰ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$2\sqrt[ 3 ]{ 2x-1 }=x^3+1$をみたす実数解を求めよ。
この動画を見る
$2\sqrt[ 3 ]{ 2x-1 }=x^3+1$をみたす実数解を求めよ。
大学入試問題#58 東海大学医学部(2021) 三角比
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師：
ますただ
問題文全文(内容文)：
$\cos^4\displaystyle \frac{\pi}{24}-\sin^4\displaystyle \frac{\pi}{24}$の値を求めよ。
出典：2021年東海大学医学部 入試問題
この動画を見る
$\cos^4\displaystyle \frac{\pi}{24}-\sin^4\displaystyle \frac{\pi}{24}$の値を求めよ。
出典：2021年東海大学医学部 入試問題
大学入試問題#57 金沢大学(2016) 整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#金沢大学
指導講師：
ますただ
問題文全文(内容文)：
$x:y$整数
$25x+9y=33$を満たすとき$|x+y|$の最小値とそのときの$x,y$の値を求めよ。
出典：2016年金沢大学 入試問題
この動画を見る
$x:y$整数
$25x+9y=33$を満たすとき$|x+y|$の最小値とそのときの$x,y$の値を求めよ。
出典：2016年金沢大学 入試問題
大学入試問題#56 立教大学(2021) 数列
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\{a_n\}:$等比数列
$\displaystyle \frac{1}{a_1}+\displaystyle \frac{1}{a_2}=3$
$\displaystyle \frac{1}{a_2}+\displaystyle \frac{1}{a_3}=2$をみたすとき
$\displaystyle \sum_{n=1}^\infty\displaystyle \frac{1}{a_n}$の値を求めよ。
出典：2021年立教大学 入試問題
この動画を見る
$\{a_n\}:$等比数列
$\displaystyle \frac{1}{a_1}+\displaystyle \frac{1}{a_2}=3$
$\displaystyle \frac{1}{a_2}+\displaystyle \frac{1}{a_3}=2$をみたすとき
$\displaystyle \sum_{n=1}^\infty\displaystyle \frac{1}{a_n}$の値を求めよ。
出典：2021年立教大学 入試問題
大学入試問題#55 早稲田大学(2021) Σの計算
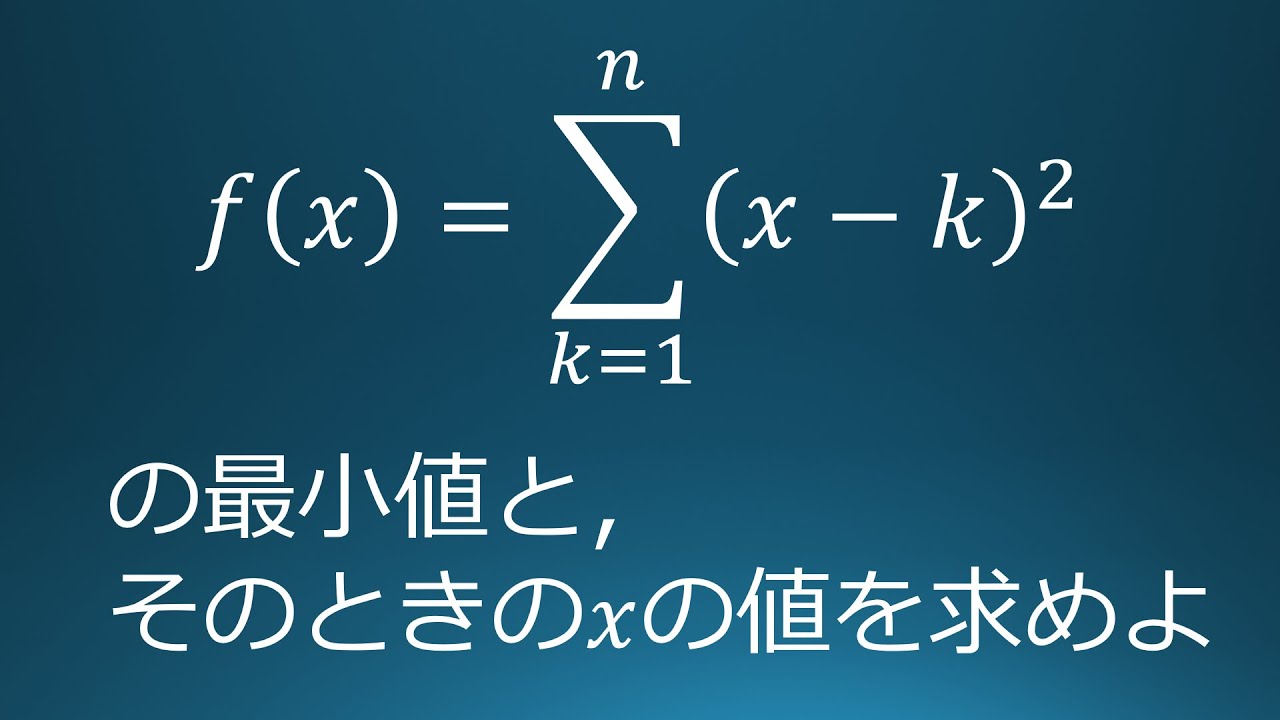
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=\displaystyle \sum_{k=1}^n(x-k)^2$の最小値とそのときの$x$の値を$n$で表せ
出典：2021年早稲田大学 入試問題
この動画を見る
$f(x)=\displaystyle \sum_{k=1}^n(x-k)^2$の最小値とそのときの$x$の値を$n$で表せ
出典：2021年早稲田大学 入試問題
大学入試問題#54 早稲田大学(2021) 積分の応用
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$m,n:$正の整数
$f(x):n:x$次関数
$\displaystyle \int_{0}^{x}(x-t)^{m-1}f(t)dt=\{f(x)\}^m$を満たすとき$f(x)$を求めよ。
出典：2021年早稲田大学 入試問題
この動画を見る
$m,n:$正の整数
$f(x):n:x$次関数
$\displaystyle \int_{0}^{x}(x-t)^{m-1}f(t)dt=\{f(x)\}^m$を満たすとき$f(x)$を求めよ。
出典：2021年早稲田大学 入試問題
大学入試問題#53 横浜市立大学(2020) 数列
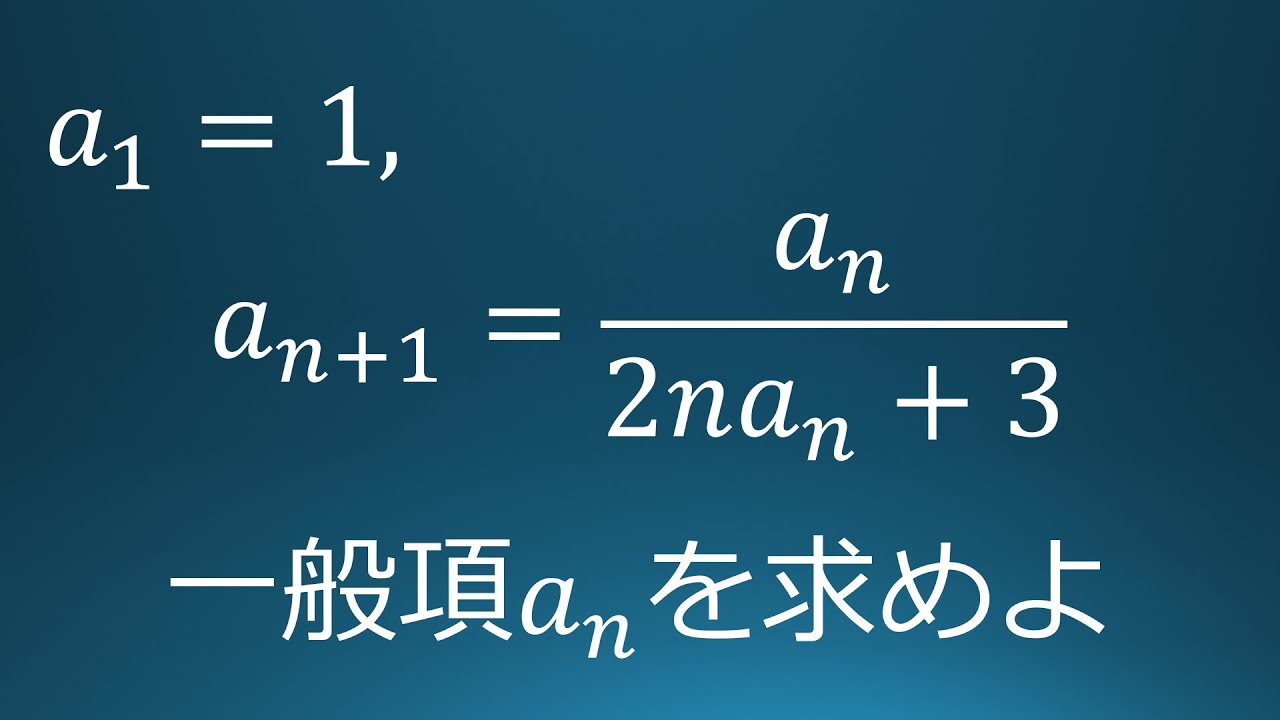
単元：
#大学入試過去問(数学)#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#数学(高校生)#数B#横浜市立大学
指導講師：
ますただ
問題文全文(内容文)：
$a_1=1$
$a_{n+1}=\displaystyle \frac{a_n}{2n\ a_n+3}$で定まる数列の一般項$a_n$を求めよ
出典：2020年横浜市立大学 入試問題
この動画を見る
$a_1=1$
$a_{n+1}=\displaystyle \frac{a_n}{2n\ a_n+3}$で定まる数列の一般項$a_n$を求めよ
出典：2020年横浜市立大学 入試問題
大学入試問題#52 防衛医科大学(2020) 複素数
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#防衛医科大学
指導講師：
ますただ
問題文全文(内容文)：
$z^3=8$の虚数解の1つを$\alpha$とする。
$\alpha^4+6\alpha^3+8\alpha^2+8\alpha$の値を求めよ。
出典：2020年防衛医科大学 入試問題
この動画を見る
$z^3=8$の虚数解の1つを$\alpha$とする。
$\alpha^4+6\alpha^3+8\alpha^2+8\alpha$の値を求めよ。
出典：2020年防衛医科大学 入試問題
#45 数検1級1次 過去問 複雑な方程式
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$3x^2-12x+8=\displaystyle \frac{i\sqrt{ x-1 }}{\sqrt{ 3 }}$を満たす実数解$x$を求めよ
この動画を見る
$3x^2-12x+8=\displaystyle \frac{i\sqrt{ x-1 }}{\sqrt{ 3 }}$を満たす実数解$x$を求めよ
#51 大学入試問題 新潟大学(2020) 定積分【King propertyっぽいけど・・・】
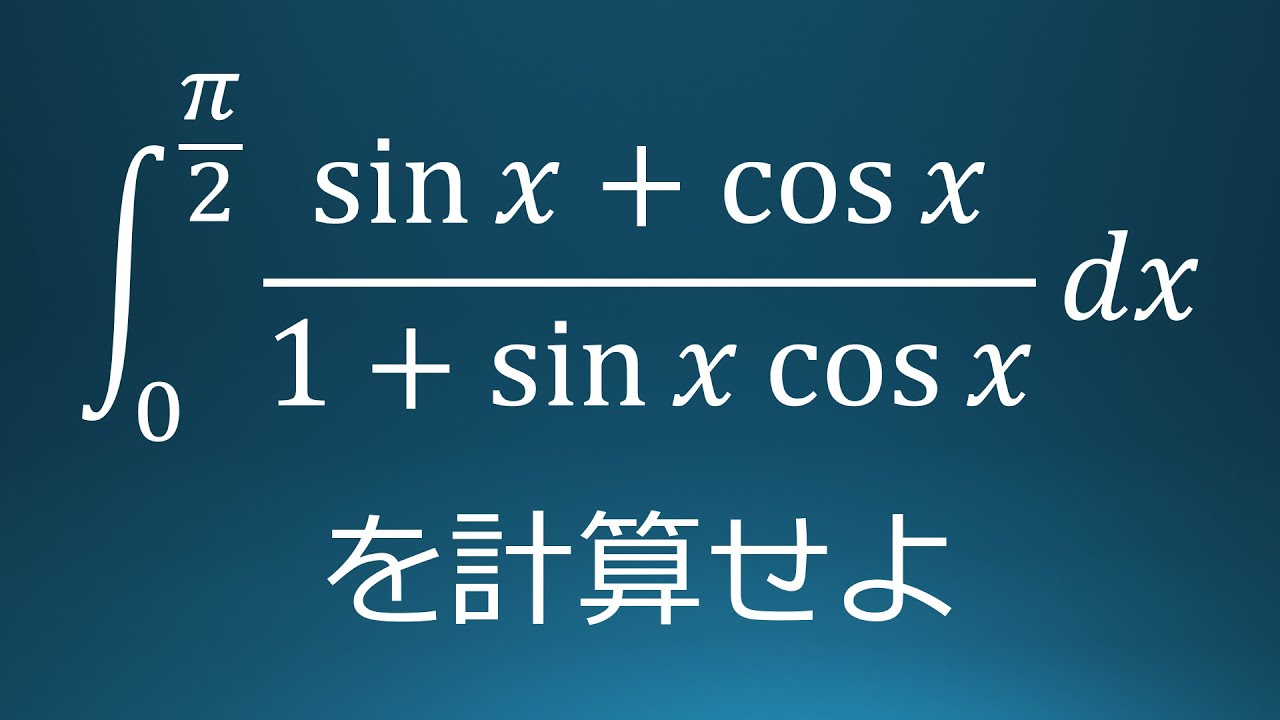
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x+\cos\ x}{1+\sin\ x\ \cos\ x}\ dx$を計算せよ。
出典：2020年新潟大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x+\cos\ x}{1+\sin\ x\ \cos\ x}\ dx$を計算せよ。
出典：2020年新潟大学 入試問題
#44 数検1級1次 過去問 3乗根
単元：
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt[ 3 ]{ 10+6\sqrt{ 3 } }$を$a+b\sqrt{ 3 }$で表せ。
ただし$a,b$は有理数とする。
この動画を見る
$\sqrt[ 3 ]{ 10+6\sqrt{ 3 } }$を$a+b\sqrt{ 3 }$で表せ。
ただし$a,b$は有理数とする。
#42 数検1級1次 過去問 極限値
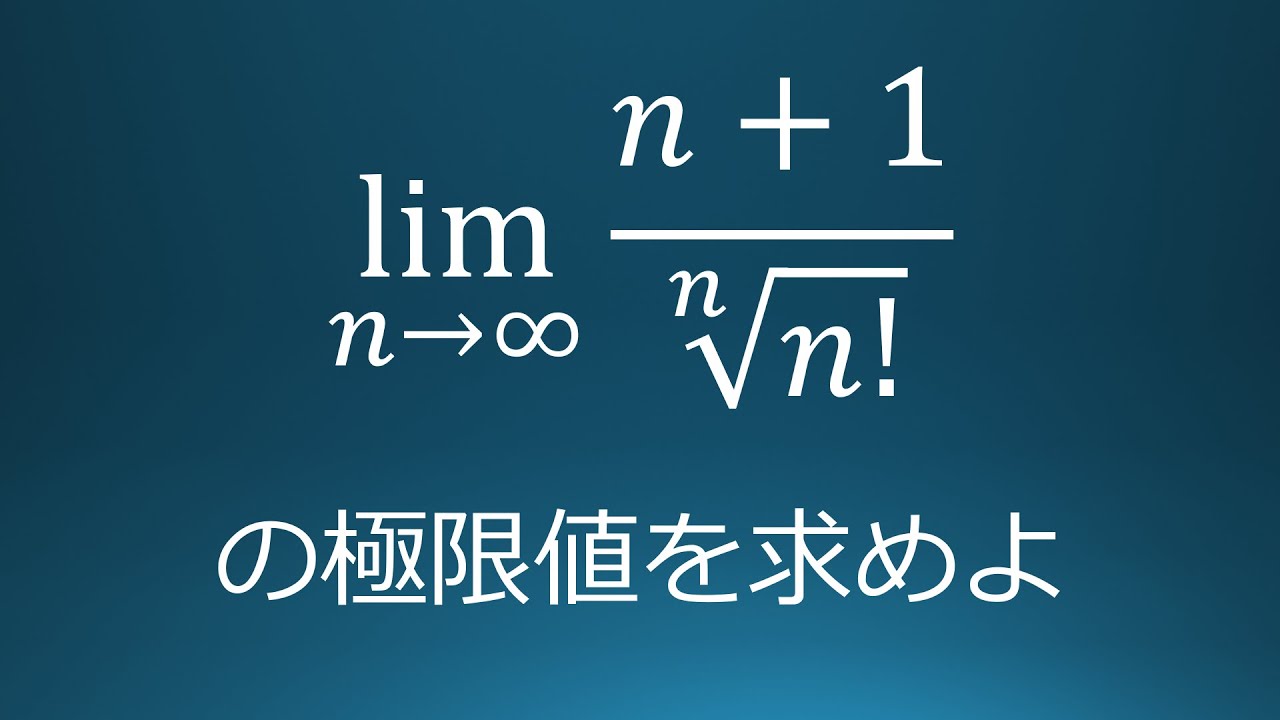
単元：
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{n+1}{\sqrt[ n ]{ n! }}$の極限値を求めよ。
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{n+1}{\sqrt[ n ]{ n! }}$の極限値を求めよ。
大学入試問題#47 横浜国立大学(2020) 複素数
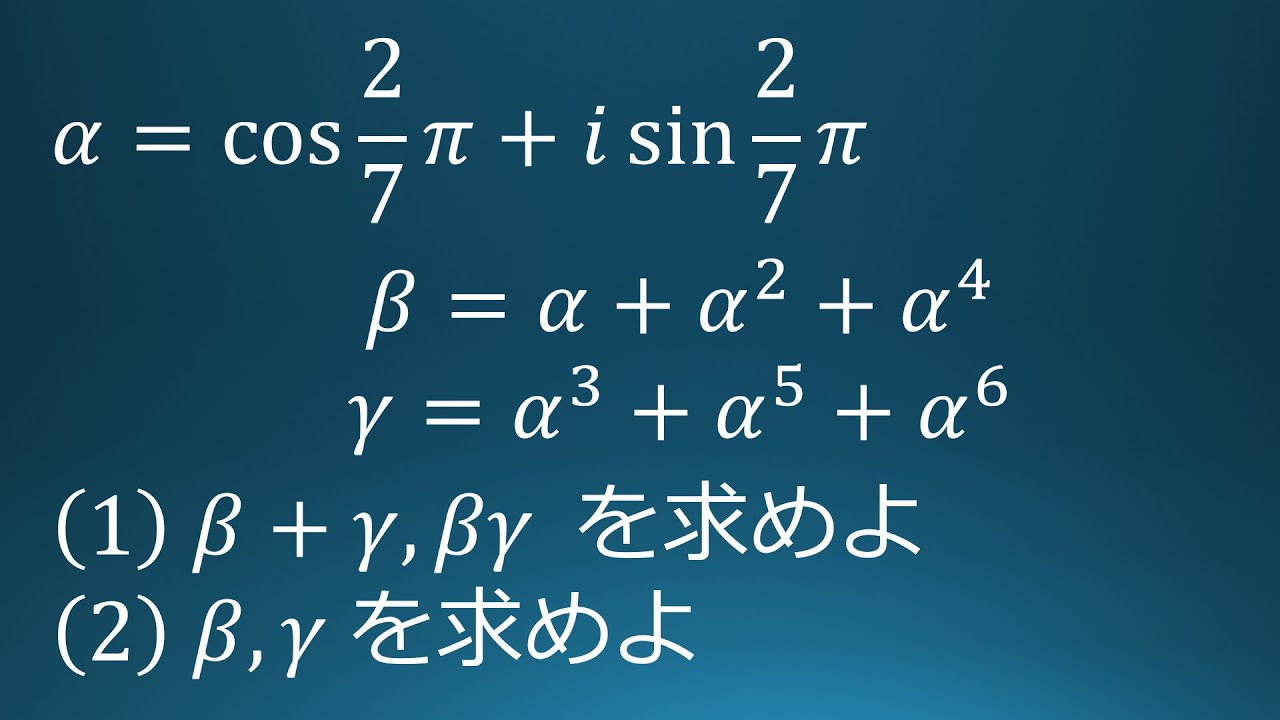
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\alpha=\cos\displaystyle \frac{2}{7}\pi+i\ \sin\displaystyle \frac{2}{7}\pi$
$\beta=\alpha+\alpha^2+\alpha^4$
$r=\alpha^3+\alpha^5+\alpha^6$
（1）$\beta+r,\ \beta\ r$を求めよ。
（2）$\beta,r$を求めよ。
出典：2020年横浜国立大学 入試問題
この動画を見る
$\alpha=\cos\displaystyle \frac{2}{7}\pi+i\ \sin\displaystyle \frac{2}{7}\pi$
$\beta=\alpha+\alpha^2+\alpha^4$
$r=\alpha^3+\alpha^5+\alpha^6$
（1）$\beta+r,\ \beta\ r$を求めよ。
（2）$\beta,r$を求めよ。
出典：2020年横浜国立大学 入試問題
大学入試問題#50 神戸大学2016 x軸回転体
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$a \gt 0$
$C_1:y=log\ x$
$c_2:y=ax^2$
$c_1$と$c_2$は接する。
$c_1,\ c_2,\ x$軸で囲まれた部分を$x$軸のまわりに1回転させてできる体積を求めよ。
出典：2016年神戸大学 入試問題
この動画を見る
$a \gt 0$
$C_1:y=log\ x$
$c_2:y=ax^2$
$c_1$と$c_2$は接する。
$c_1,\ c_2,\ x$軸で囲まれた部分を$x$軸のまわりに1回転させてできる体積を求めよ。
出典：2016年神戸大学 入試問題
大学入試問題#49 神戸大学(2021) 極値の判定
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$a$：実数
$f(x)=ax+\cos\ x+\displaystyle \frac{1}{2}\sin2x$が極値をもたないように$a$の値の範囲を求めよ。
出典：2010年神戸大学 入試問題
この動画を見る
$a$：実数
$f(x)=ax+\cos\ x+\displaystyle \frac{1}{2}\sin2x$が極値をもたないように$a$の値の範囲を求めよ。
出典：2010年神戸大学 入試問題
大学入試問題#48 神戸大学(2021) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{1}x^3log(x^2+1)dx$を計算せよ。
出典：2021年神戸大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}x^3log(x^2+1)dx$を計算せよ。
出典：2021年神戸大学 入試問題
#40 数検1級１次 過去問 微分方程式
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$3y\displaystyle \frac{d^2y}{dx^2}+(\displaystyle \frac{dy}{dx})^2=0$において
$x=0$のとき$y=0$
$X=1$のとき$y=1$
を満たす特殊解を求めよ。
この動画を見る
$3y\displaystyle \frac{d^2y}{dx^2}+(\displaystyle \frac{dy}{dx})^2=0$において
$x=0$のとき$y=0$
$X=1$のとき$y=1$
を満たす特殊解を求めよ。
大学入試問題#46 岡山大学(2013) 曲面で囲まれた領域の面積
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岡山大学
指導講師：
ますただ
問題文全文(内容文)：
$x \gt 0$
曲線$y=|x-\displaystyle \frac{1}{x}|$と直線$y=2$で囲まれた領域の面積$S$を求めよ
出典：2013年岡山大学 入試問題
この動画を見る
$x \gt 0$
曲線$y=|x-\displaystyle \frac{1}{x}|$と直線$y=2$で囲まれた領域の面積$S$を求めよ
出典：2013年岡山大学 入試問題
大学入試問題#45 岡山大学(2011) 行列
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岡山大学
指導講師：
ますただ
問題文全文(内容文)：
$t$:実数
$A=(\begin{eqnarray}
t\ t-1 \\
1-t\ 2-t
\end{eqnarray})$
$A^{2n}-tA^n$が$n$の値によらない行列になるとき、$t$の値を求めよ。
出典：2011年岡山大学 入試問題
この動画を見る
$t$:実数
$A=(\begin{eqnarray}
t\ t-1 \\
1-t\ 2-t
\end{eqnarray})$
$A^{2n}-tA^n$が$n$の値によらない行列になるとき、$t$の値を求めよ。
出典：2011年岡山大学 入試問題
#39 数検1級1次 過去問 解と係数の関係 整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$m,n:$正の整数
$x^3-mx^2+nx-n=0$のすべての解が正の整数であるような組$(m,n)$を求めよ。
この動画を見る
$m,n:$正の整数
$x^3-mx^2+nx-n=0$のすべての解が正の整数であるような組$(m,n)$を求めよ。
#38 数検1級1次 過去問 解と係数の関係
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$z^3+2z^2+2z+1=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^{2019}+\beta^{2019}+\gamma^{2019}$の値を求めよ。
この動画を見る
$z^3+2z^2+2z+1=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^{2019}+\beta^{2019}+\gamma^{2019}$の値を求めよ。