ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
高専数学 微積I #226(2) 媒介変数表示の面積
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$0\leqq t\leqq \dfrac{\pi}{4}$とする.
曲線$x=\tan t,y=\sin t+1$と
$x$軸,$y$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
この動画を見る
$0\leqq t\leqq \dfrac{\pi}{4}$とする.
曲線$x=\tan t,y=\sin t+1$と
$x$軸,$y$軸,直線$x=1$で囲まれた図形の
面積$S$を求めよ.
16和歌山県教員採用試験（数学：5番 整数問題）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}$
$n$が整数のとき,
$2n^3-3n^2+n$は6の倍数であることを示せ.
この動画を見る
$\boxed{5}$
$n$が整数のとき,
$2n^3-3n^2+n$は6の倍数であることを示せ.
ε N論法 #6 1-n^2(n→∞)
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty}(1-n^2)=-\infty$
$ε N$論法で証明せよ.
この動画を見る
$\displaystyle \lim_{n\to\infty}(1-n^2)=-\infty$
$ε N$論法で証明せよ.
ε N論法 #5 √n(n→∞）
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty} \sqrt n=+\infty$
$ε N$論法で証明せよ.
この動画を見る
$\displaystyle \lim_{n\to\infty} \sqrt n=+\infty$
$ε N$論法で証明せよ.
高専数学 微積I #226(1) 媒介変数表示の面積
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#媒介変数表示と極座標#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$0\leqq t\leqq 1$とする.
曲線$x=t^2,y=t^2-2t+1$
$x$軸,$y$軸で囲まれた図形の
面積$S$を求めよ.
この動画を見る
$0\leqq t\leqq 1$とする.
曲線$x=t^2,y=t^2-2t+1$
$x$軸,$y$軸で囲まれた図形の
面積$S$を求めよ.
兵庫県教員採用試験（数学：練習問題 解の個数）
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$a\gt 0$とする.
$x^a=a^x$を満たす正の解の
個数を調べよ.
この動画を見る
$a\gt 0$とする.
$x^a=a^x$を満たす正の解の
個数を調べよ.
高専数学 微積I #218 曲線の長さの最小値 （九州大学類題）
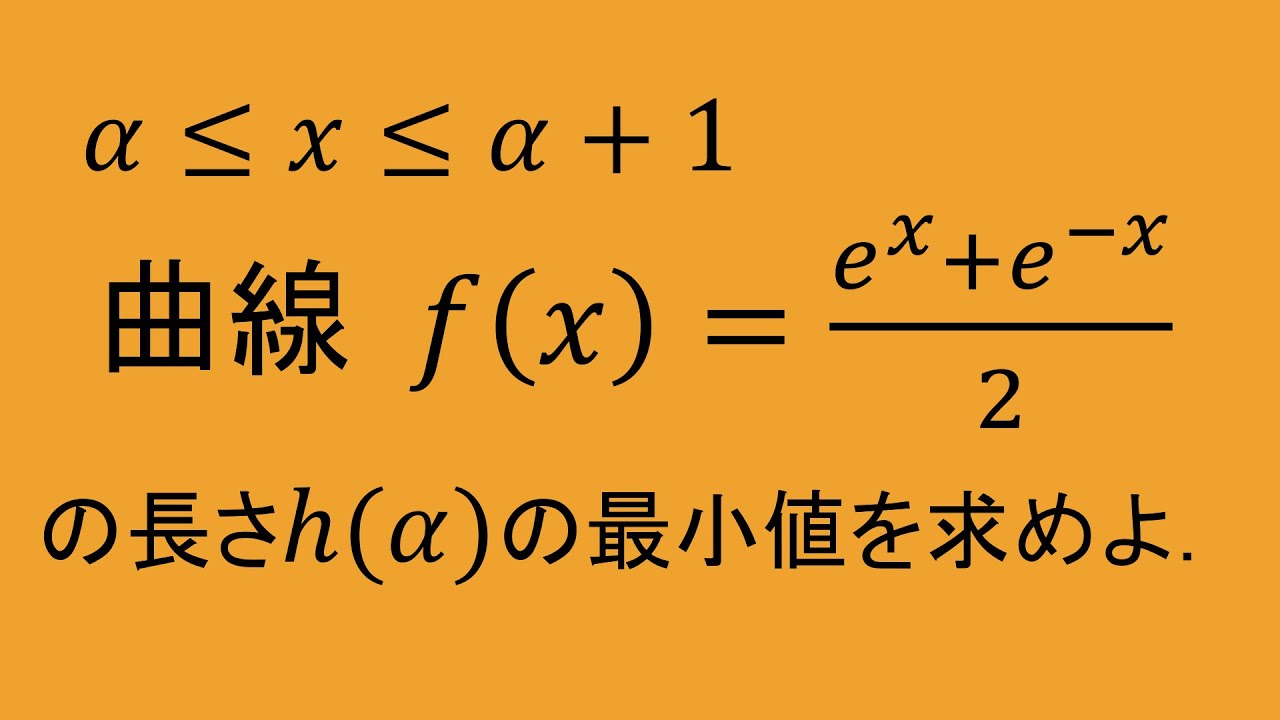
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=\dfrac{e^x+e^{-x}}{2} \ (\alpha \leqq x \leqq \alpha+1)$
の曲線の長さ$k(\alpha)$の最小値を求めよ.
この動画を見る
$f(x)=\dfrac{e^x+e^{-x}}{2} \ (\alpha \leqq x \leqq \alpha+1)$
の曲線の長さ$k(\alpha)$の最小値を求めよ.
16和歌山県教員採用試験（数学：6番 対数の不等式）
単元：
#数Ⅰ#数Ⅱ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{6}$
$2\log_3 x-4\log_x 27 \leqq 5$を解け.
この動画を見る
$\boxed{6}$
$2\log_3 x-4\log_x 27 \leqq 5$を解け.
11滋賀県教員採用試験（数学：1-(4) 剰余・因数定理系）
単元：
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}-(4)$
$f(x)=x^4+px^2+gx-8$は
$(x+1)^2$で割り切れるとき,
$p,q$の値を求めよ.
この動画を見る
$\boxed{1}-(4)$
$f(x)=x^4+px^2+gx-8$は
$(x+1)^2$で割り切れるとき,
$p,q$の値を求めよ.
高専数学 微積I #211 体積
単元：
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
半径$r$の直円柱を底面の直径$AB$を通り
底面と$\dfrac{\pi}{6}$の角をなす平面で切るとき,
底面と平面の間の部分の体積$V$を求めよ.
この動画を見る
半径$r$の直円柱を底面の直径$AB$を通り
底面と$\dfrac{\pi}{6}$の角をなす平面で切るとき,
底面と平面の間の部分の体積$V$を求めよ.
15滋賀県教員採用試験（数学：5番 グラフと極限）
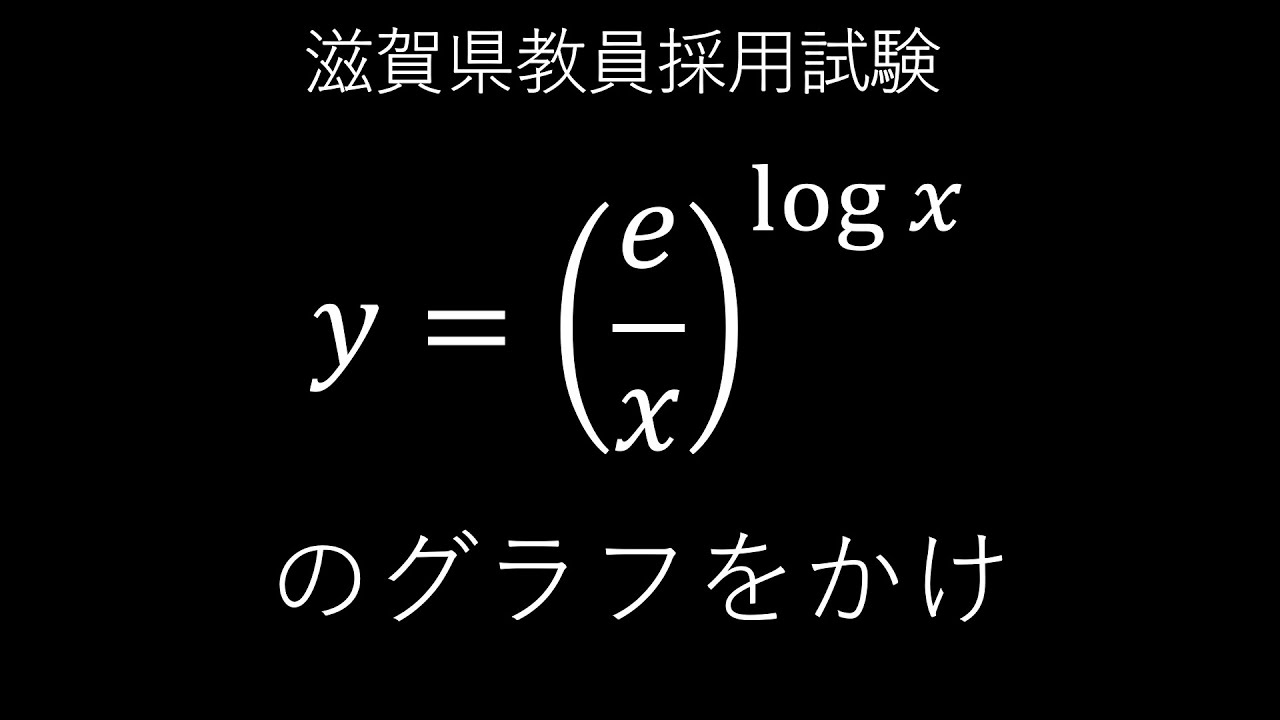
単元：
#関数と極限#微分とその応用#数列の極限#関数の極限#関数の変化（グラフ・最大最小・方程式・不等式）#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}$
$y=\left(\dfrac{e}{x}\right)^{\log x}$のグラフをかけ.
この動画を見る
$\boxed{5}$
$y=\left(\dfrac{e}{x}\right)^{\log x}$のグラフをかけ.
高専数学 微積I #210(2) 曲線の長さ
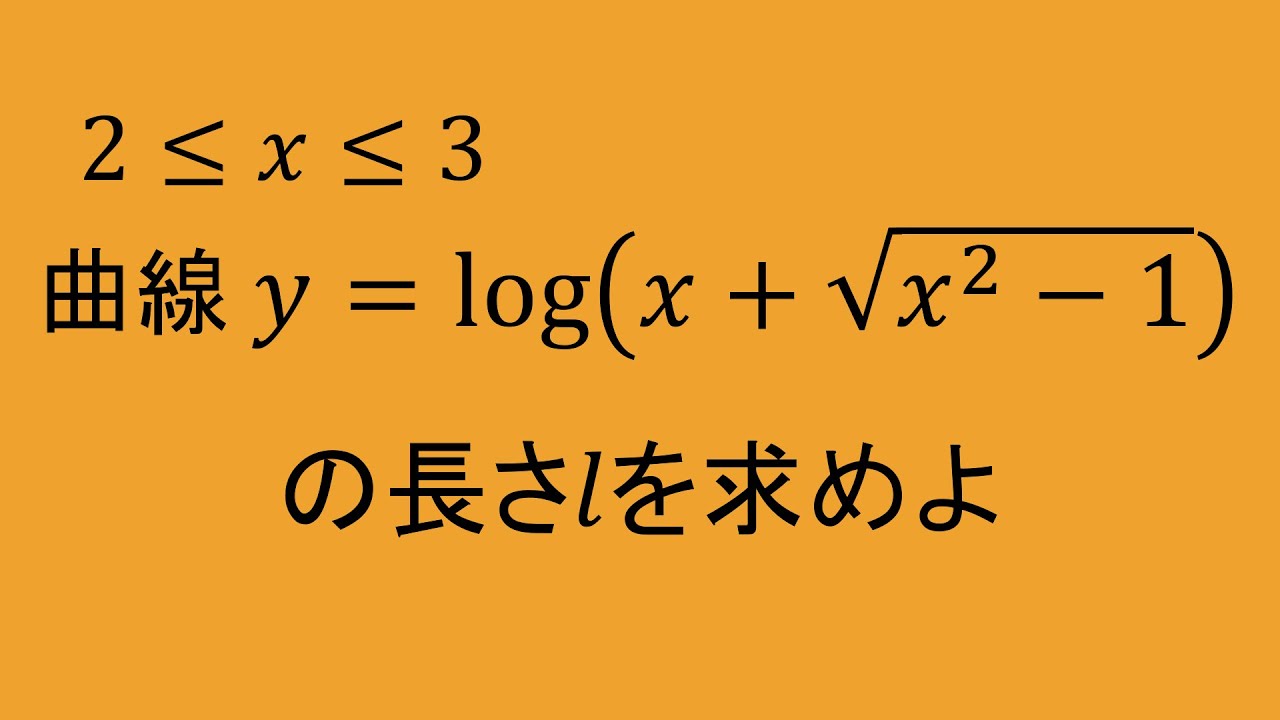
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$2\leqq x\leqq 3$
曲線$y=\log (x+\sqrt{x^2-1})$の長さ$\ell$を求めよ.
この動画を見る
$2\leqq x\leqq 3$
曲線$y=\log (x+\sqrt{x^2-1})$の長さ$\ell$を求めよ.
高専数学 微積I #210(1) 曲線の長さ
単元：
#数Ⅱ#平面上の曲線#微分法と積分法#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
曲線$y=(x-1)^{\frac{3}{2}} \ (1\leq x \leq 6)$
の長さ$\ell$を求めよ.
この動画を見る
曲線$y=(x-1)^{\frac{3}{2}} \ (1\leq x \leq 6)$
の長さ$\ell$を求めよ.
07滋賀県教員採用試験（数学：5番 接線の個数）
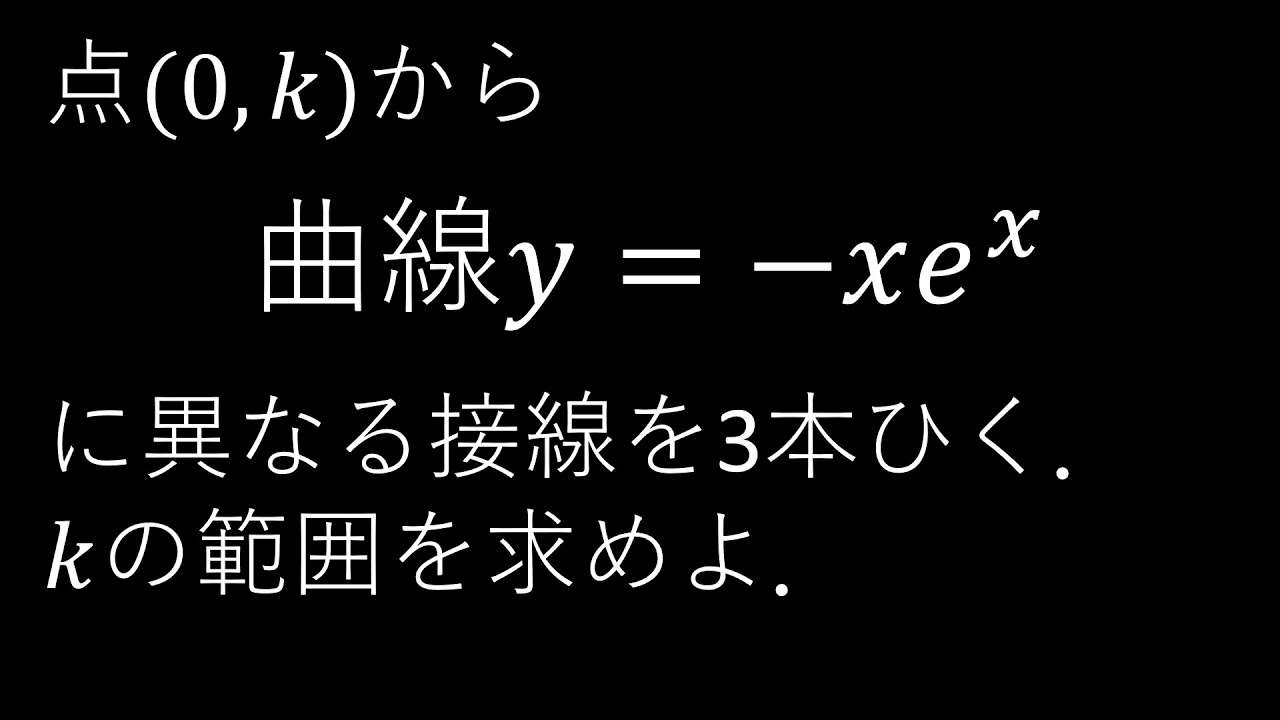
単元：
#微分とその応用#接線と法線・平均値の定理#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}$
点$(0,k)$から曲線$c$
$c:y=-xe^x$
に異なる3本の接線が引けるとき,
$k$の値の範囲を求めよ.
この動画を見る
$\boxed{5}$
点$(0,k)$から曲線$c$
$c:y=-xe^x$
に異なる3本の接線が引けるとき,
$k$の値の範囲を求めよ.
ε-N論法 #3 lim n/n+2 =1
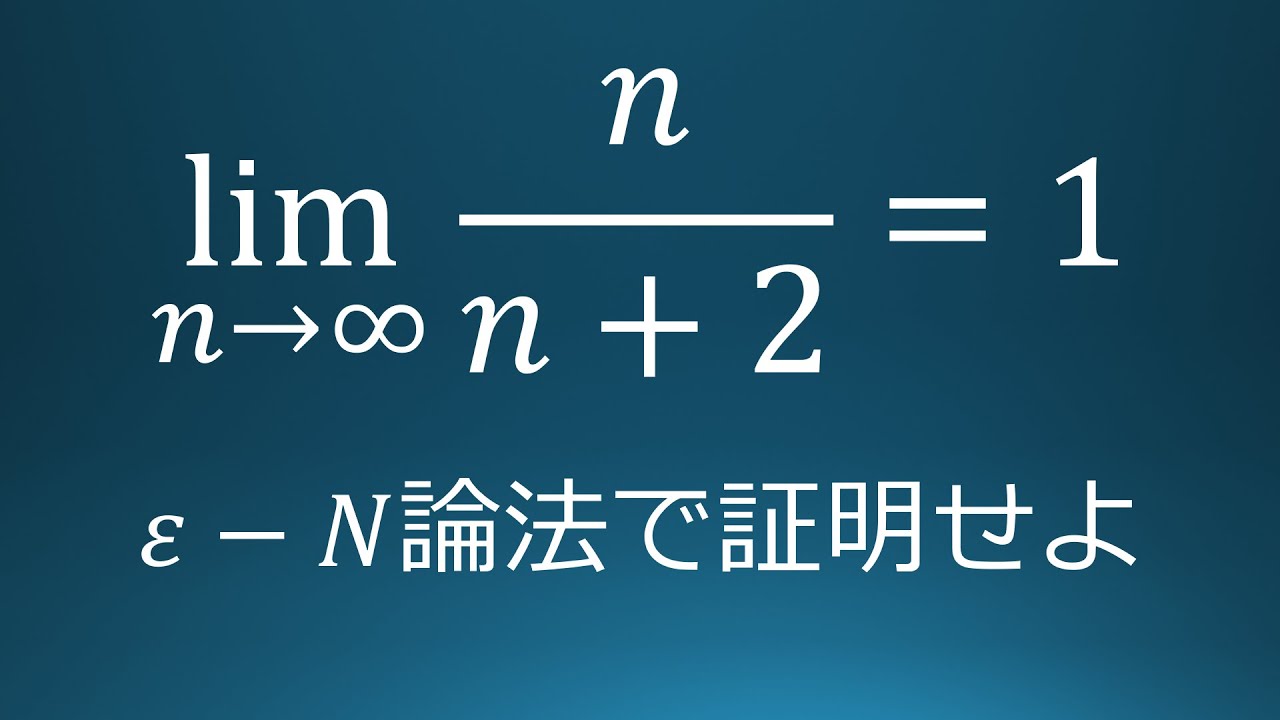
単元：
#数Ⅱ#式と証明#微分法と積分法#恒等式・等式・不等式の証明#平均変化率・極限・導関数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty} \dfrac{n}{n+2}=1$を
$ε-N$論法を利用して示せ.
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{n}{n+2}=1$を
$ε-N$論法を利用して示せ.
ε-N論法 #2 lim 1/n^2=0
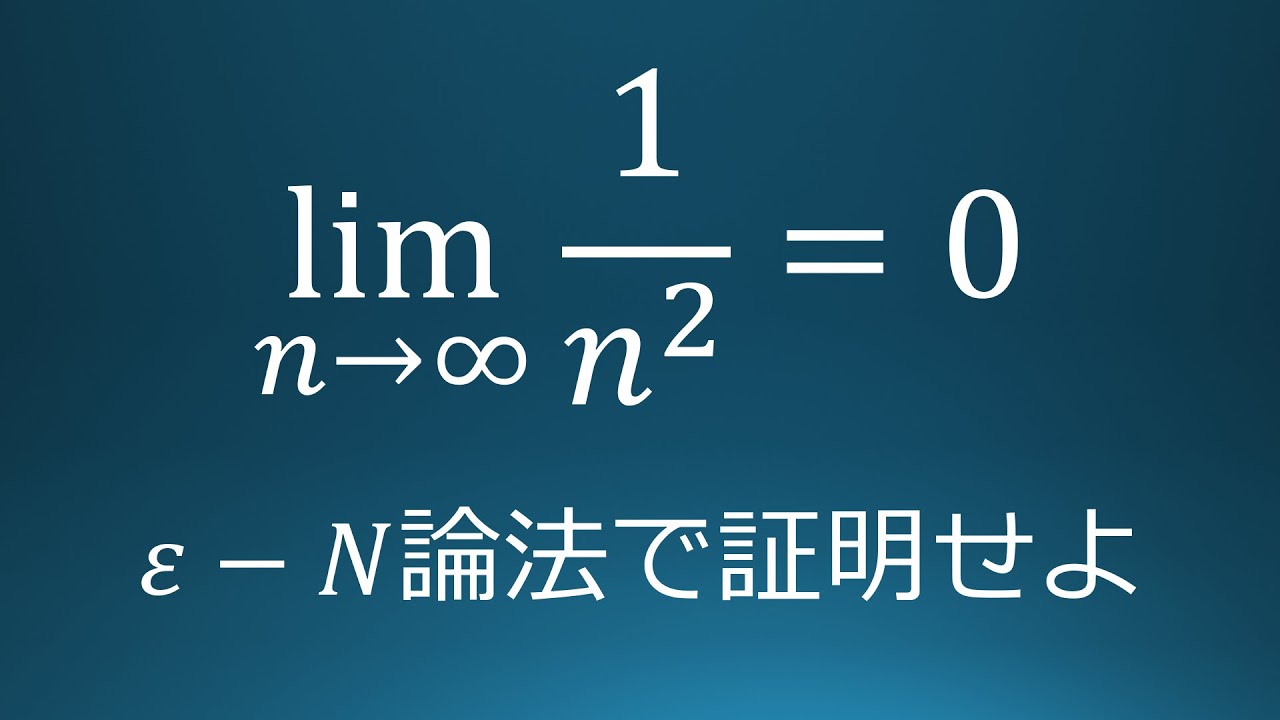
単元：
#数Ⅱ#式と証明#微分法と積分法#恒等式・等式・不等式の証明#平均変化率・極限・導関数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty} \dfrac{1}{n^2}=0$を
$ε-N$論法を利用して示せ.
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{1}{n^2}=0$を
$ε-N$論法を利用して示せ.
高専数学 微積I #207 体積
単元：
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
点$x(0\lt x\lt \pi)$で$x$軸に垂直な平面で切った切り口が,
辺の長さが$x,\sin x$の長方形である立体の体積$V$を求めよ.
この動画を見る
点$x(0\lt x\lt \pi)$で$x$軸に垂直な平面で切った切り口が,
辺の長さが$x,\sin x$の長方形である立体の体積$V$を求めよ.
12滋賀県教員採用試験（数学：5番 微分と微分方程式）
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{5}$任意の実数$s,t$に対して
$f(s+t)=f(s)f(t),f(1)\neq 0,f`(0)=a$である.
(1)$f(0)$
(2)任意の実数$x$に対して$f(x)\neq 0$を示せ.
(3)任意の実数$x$に対して$f`(x)=af(x)$を示せ.
(4)$f(x)$を求めよ.
この動画を見る
$\boxed{5}$任意の実数$s,t$に対して
$f(s+t)=f(s)f(t),f(1)\neq 0,f`(0)=a$である.
(1)$f(0)$
(2)任意の実数$x$に対して$f(x)\neq 0$を示せ.
(3)任意の実数$x$に対して$f`(x)=af(x)$を示せ.
(4)$f(x)$を求めよ.
ε-N論法 #1 lim1/n=0
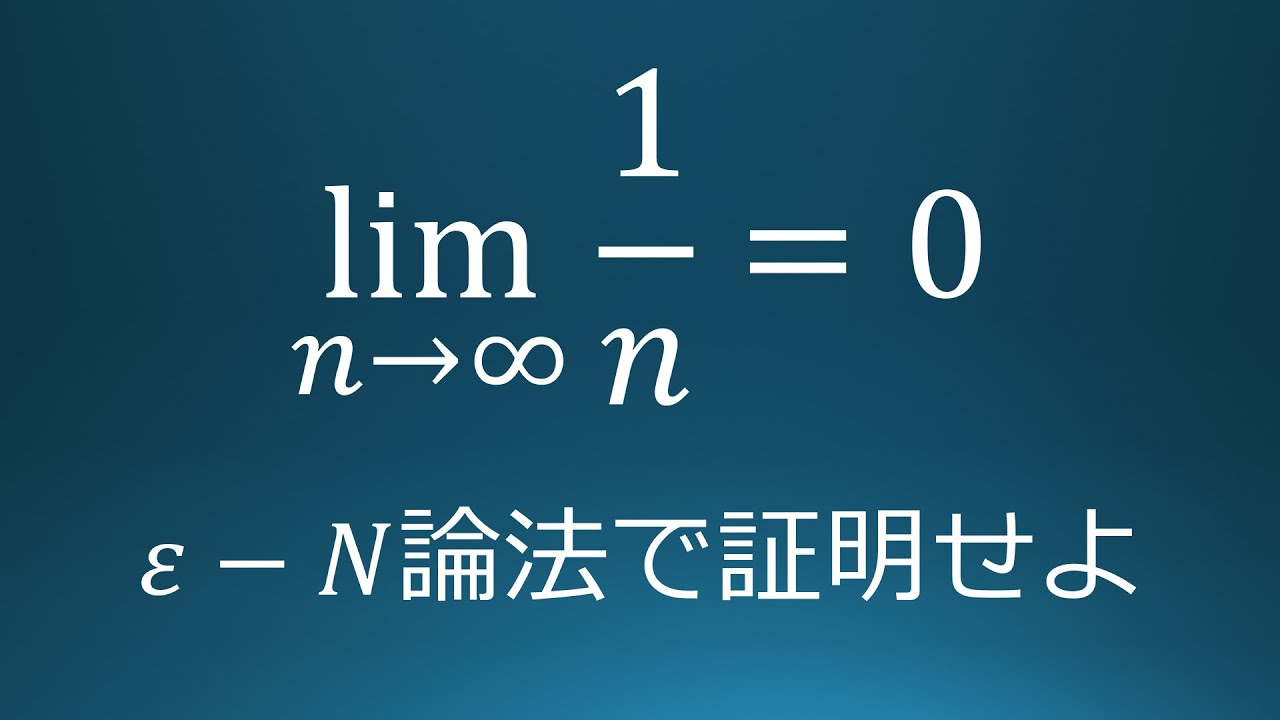
単元：
#数Ⅱ#式と証明#微分法と積分法#恒等式・等式・不等式の証明#平均変化率・極限・導関数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{n\to\infty} \dfrac{1}{n}=0$を
$ε-N$論法を利用して示せ.
この動画を見る
$\displaystyle \lim_{n\to\infty} \dfrac{1}{n}=0$を
$ε-N$論法を利用して示せ.
ε-N論法 #4 はさみうちの原理
単元：
#数Ⅱ#式と証明#微分法と積分法#恒等式・等式・不等式の証明#平均変化率・極限・導関数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
各自然数$n$で$a_n \leqq b_n \leqq c_n$を
満たす任意の数列
{$a_n$},{$b_n$},{$c_n$}に対して
$\displaystyle \lim_{n\to\infty} a_n=A=\displaystyle \lim_{n\to\infty} c_n$
ならば
$\displaystyle \lim_{n\to\infty} b_n=A$
ε-N論法で証明せよ.
この動画を見る
各自然数$n$で$a_n \leqq b_n \leqq c_n$を
満たす任意の数列
{$a_n$},{$b_n$},{$c_n$}に対して
$\displaystyle \lim_{n\to\infty} a_n=A=\displaystyle \lim_{n\to\infty} c_n$
ならば
$\displaystyle \lim_{n\to\infty} b_n=A$
ε-N論法で証明せよ.
高専数学 微積I #206 体積
単元：
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
3辺の長さが3,4,5の三角形を底面とする高さが
10の三角錐の体積$V$を求めよ.
この動画を見る
3辺の長さが3,4,5の三角形を底面とする高さが
10の三角錐の体積$V$を求めよ.
15岡山県教員採用試験（数学：2次方程式）
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$kx^2-4x+k-3=0$が異なる2つの実数解をもつ.
$k$の値の範囲を求めよ.
この動画を見る
$kx^2-4x+k-3=0$が異なる2つの実数解をもつ.
$k$の値の範囲を求めよ.
岡山県教員採用試験：方程式の利用
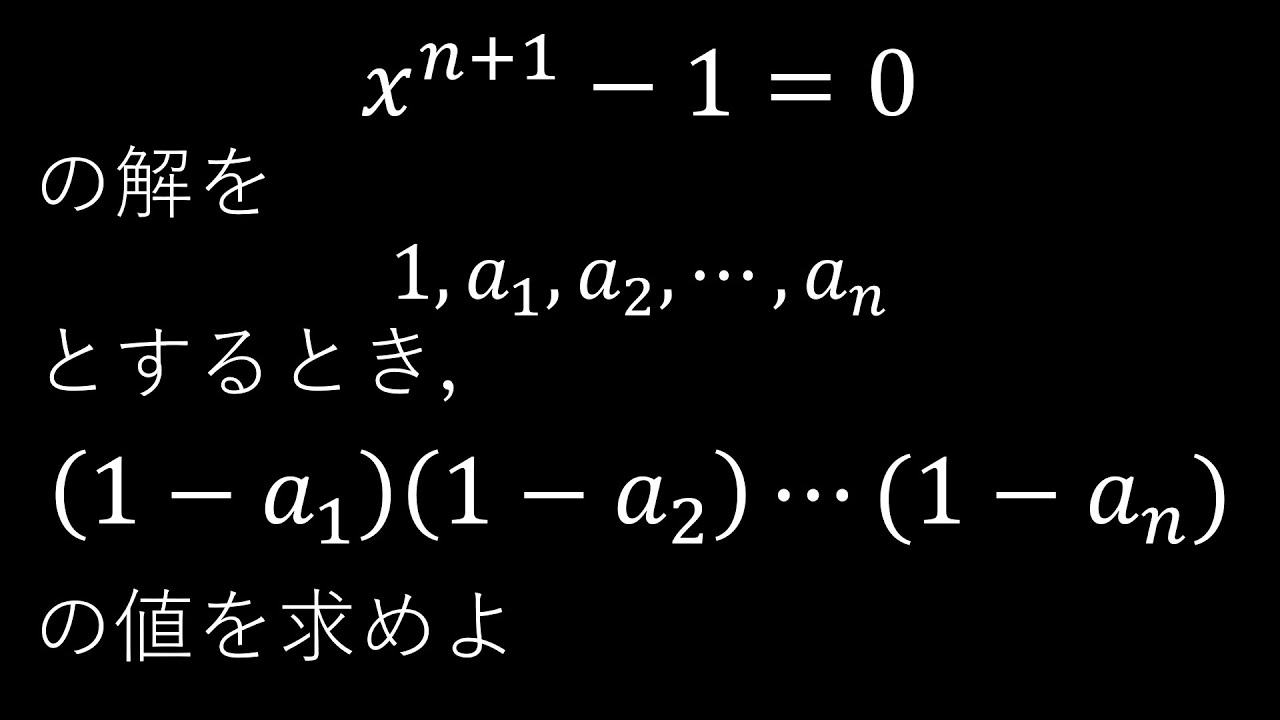
単元：
#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}$ $n$は自然数とする.
$x^{n+1}-1=0$の解を
$1,a_1,a_2,･･･,a_n$とするとき,
$(1-a_1)\times (1-a_2)\times ･･･ \times (1-a_n)$
の値を求めよ.
この動画を見る
$\boxed{1}$ $n$は自然数とする.
$x^{n+1}-1=0$の解を
$1,a_1,a_2,･･･,a_n$とするとき,
$(1-a_1)\times (1-a_2)\times ･･･ \times (1-a_n)$
の値を求めよ.
高専数学：微積I #205 曲線の長さ
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
次の曲線の長さ$\ell$を求めよ.
(1)$y=\dfrac{1}{3} (x+1)^{1\frac{3}{2}} (-1\leqq x\leqq 4)$
(2)$y=\dfrac{1}{3}x^3+\dfrac{1}{4x} (1\leqq x\leqq 3)$
この動画を見る
次の曲線の長さ$\ell$を求めよ.
(1)$y=\dfrac{1}{3} (x+1)^{1\frac{3}{2}} (-1\leqq x\leqq 4)$
(2)$y=\dfrac{1}{3}x^3+\dfrac{1}{4x} (1\leqq x\leqq 3)$
練習問題32 整数問題 岡山大学文系類題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#岡山大学
指導講師：
ますただ
問題文全文(内容文)：
$2^{n+3},2^n$を$7$で割った余りが等しいこと
を示せ.
この動画を見る
$2^{n+3},2^n$を$7$で割った余りが等しいこと
を示せ.
06岡山教員採用試験（数学：対数の計算）
19滋賀県教員採用試験（数学：2番 整数問題）
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{2}$
$n$を整数とする.
$n^5-n$は30の倍数であることを示せ.
この動画を見る
$\boxed{2}$
$n$を整数とする.
$n^5-n$は30の倍数であることを示せ.
高専数学：微積I #204 曲線の長さ
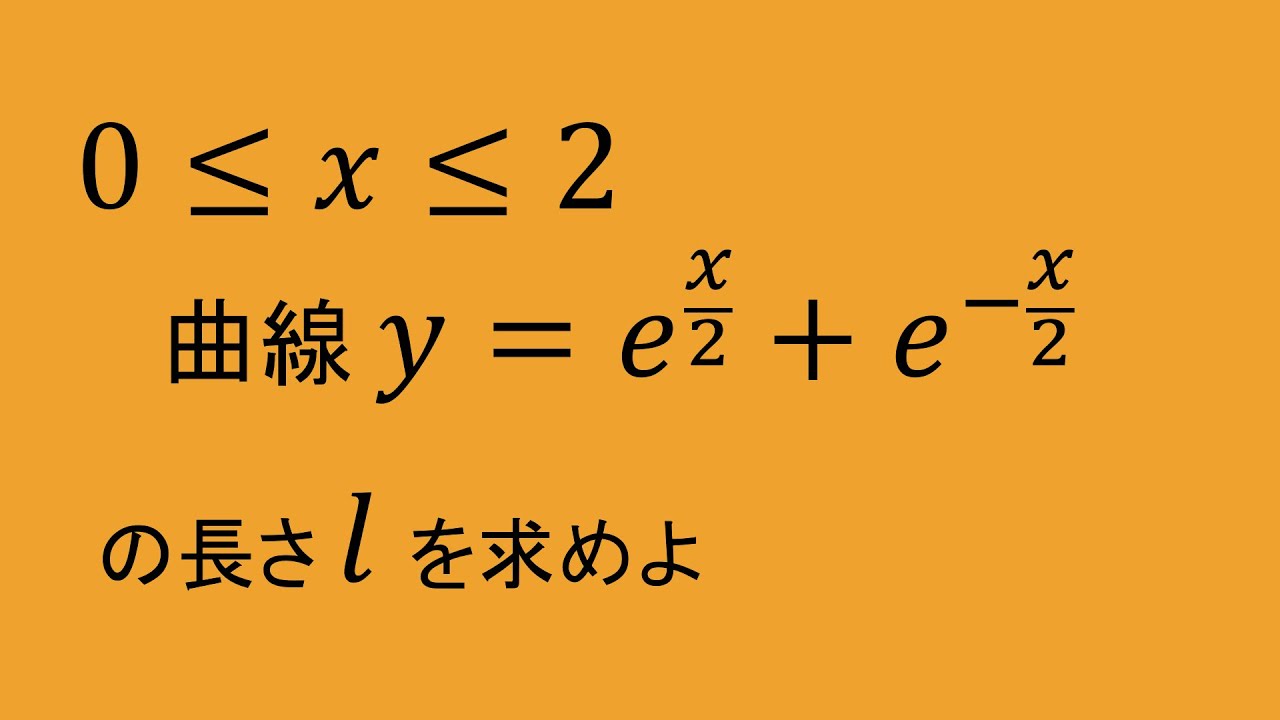
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
曲線$y=e^{\frac{x}{2}}+e^{-\frac{x}{2}} (0\leqq x\leqq 2)$
の長さ$\ell$を求めよ.
この動画を見る
曲線$y=e^{\frac{x}{2}}+e^{-\frac{x}{2}} (0\leqq x\leqq 2)$
の長さ$\ell$を求めよ.
兵庫県教員採用試験（数学：12番 極限値）
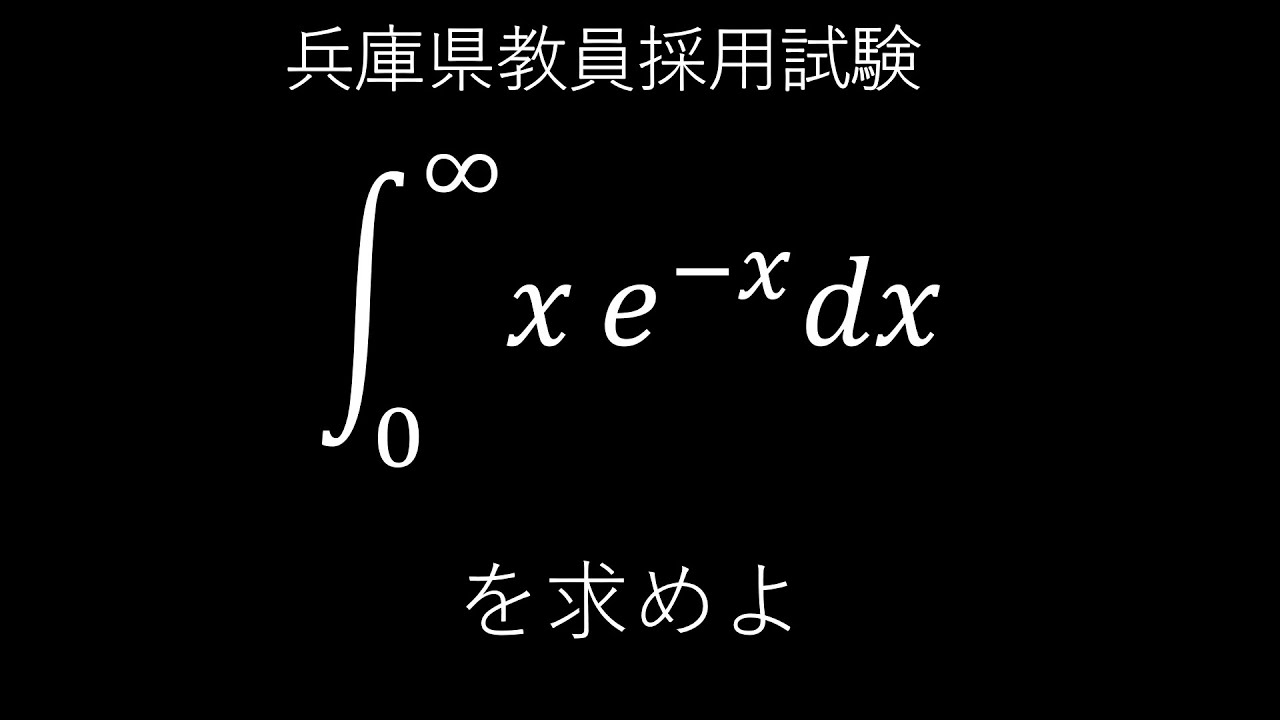
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{12}$
$\displaystyle \int_{0}^{\infty} \ x\ e^{-x} dx$を求めよ.
*$\displaystyle \lim_{t\to\infty}\dfrac{t}{e^t}=0$は利用してよい.
この動画を見る
$\boxed{12}$
$\displaystyle \int_{0}^{\infty} \ x\ e^{-x} dx$を求めよ.
*$\displaystyle \lim_{t\to\infty}\dfrac{t}{e^t}=0$は利用してよい.
岡山県教員採用試験：数学 極限値
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{x\to\infty} \left(\sin\sqrt{x+a}-\sin\sqrt x\right)$
の値を求めよ.
この動画を見る
$\displaystyle \lim_{x\to\infty} \left(\sin\sqrt{x+a}-\sin\sqrt x\right)$
の値を求めよ.