ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
06大阪府教員採用試験（数学：4番 式変形）
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{4}$ $x^5=1,x\neq 1$とする.これを解け.
(1)$x +\dfrac{1}{x}$
(2)$2x+\dfrac{1}{x+1}+\dfrac{x}{x^2+1}+\dfrac{x^2}{x^3+1}+\dfrac{x^3}{x^4+1}$
この動画を見る
$\boxed{4}$ $x^5=1,x\neq 1$とする.これを解け.
(1)$x +\dfrac{1}{x}$
(2)$2x+\dfrac{1}{x+1}+\dfrac{x}{x^2+1}+\dfrac{x^2}{x^3+1}+\dfrac{x^3}{x^4+1}$
重積分⑧-5 #154 【一般の変数変換(難)】（高専数学 微積II，数検1級1次解析対応）
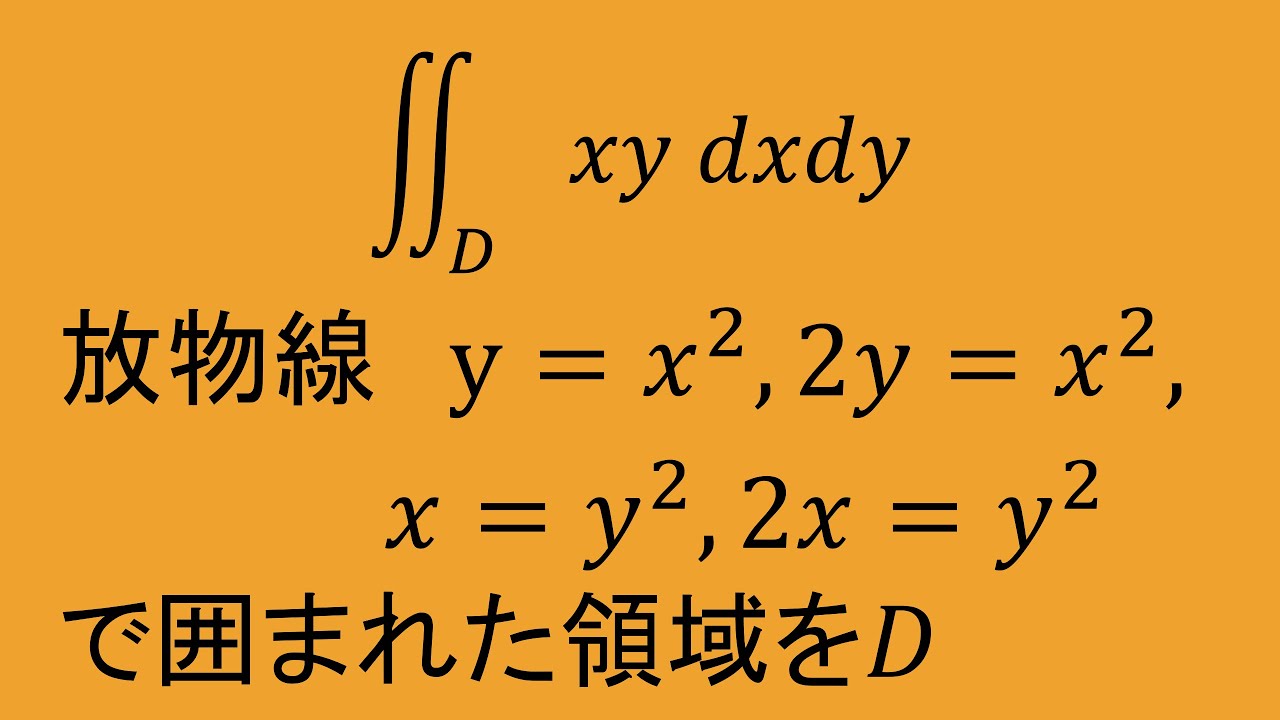
単元：
#数Ⅱ#微分法と積分法#積分とその応用#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\iint_D \ xy\ dx\ dy$
$D:y=x^2,2y=x^2,x=y^2,2x=y^2$で囲まれた領域を求めよ.
この動画を見る
$\iint_D \ xy\ dx\ dy$
$D:y=x^2,2y=x^2,x=y^2,2x=y^2$で囲まれた領域を求めよ.
13愛知県教員採用試験（数学：10番 積分）
単元：
#積分とその応用#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{10}$これを解け.
$\displaystyle \int_{0}^{\frac{\pi}{2}}\sin\dfrac{5}{2}x\cos\dfrac{1}{2}x\ dx$
この動画を見る
$\boxed{10}$これを解け.
$\displaystyle \int_{0}^{\frac{\pi}{2}}\sin\dfrac{5}{2}x\cos\dfrac{1}{2}x\ dx$
重積分⑦-6 #153-(3)【極座標による変数変換】（高専数学 微積II，数検1級対応）
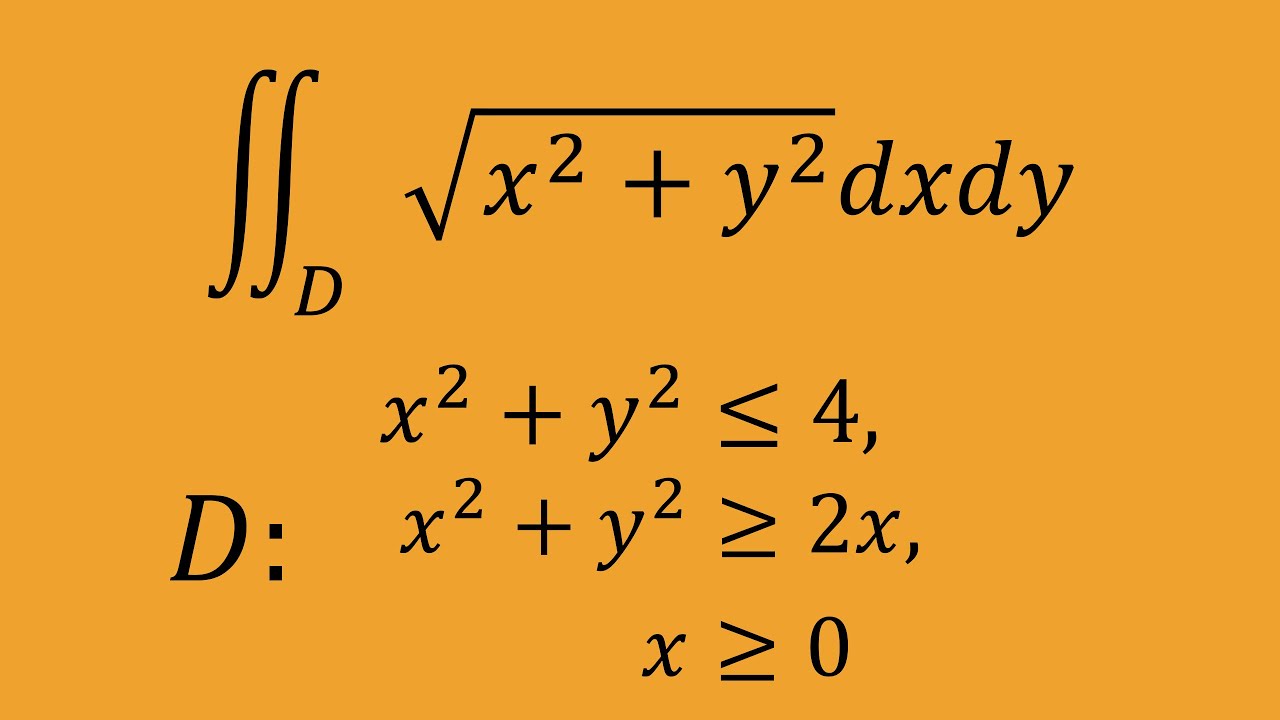
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
これを解け.
$\iint_D \ \sqrt{x^2+y^2}\ dx \ dy$
$D:x^2+y^2\leqq 4,x^2+y^2\geqq 2x,x\geqq 0$
この動画を見る
これを解け.
$\iint_D \ \sqrt{x^2+y^2}\ dx \ dy$
$D:x^2+y^2\leqq 4,x^2+y^2\geqq 2x,x\geqq 0$
04愛知県教員採用試験（数学：4番 数列）
単元：
#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{4}$
$a_1=1,a_{n+1}=a_n+\dfrac{1}{n(n+1)}$
一般項$a_n$を求めよ.
この動画を見る
$\boxed{4}$
$a_1=1,a_{n+1}=a_n+\dfrac{1}{n(n+1)}$
一般項$a_n$を求めよ.
重積分⑫-3 #152【図形Dの重心】（高専数学 微積II，数検1級1次解析対応）
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$D:-1\leqq x\leqq 1,0\leqq y\leqq x^2+1$
図形$D$の重心座標$(\overline{x},\overline{y})$を求めよ.
この動画を見る
$D:-1\leqq x\leqq 1,0\leqq y\leqq x^2+1$
図形$D$の重心座標$(\overline{x},\overline{y})$を求めよ.
03愛知県教員採用試験（数学：13 極限値）
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{13}$これを解け.
$\displaystyle \lim_{x\to 0}\ \dfrac{\sin^{-1}x-x}{x^3}$
この動画を見る
$\boxed{13}$これを解け.
$\displaystyle \lim_{x\to 0}\ \dfrac{\sin^{-1}x-x}{x^3}$
ε-δ論法 #3 f(x)=e^x が連続
ε-δ論法 #2 f(x)=log x が連続
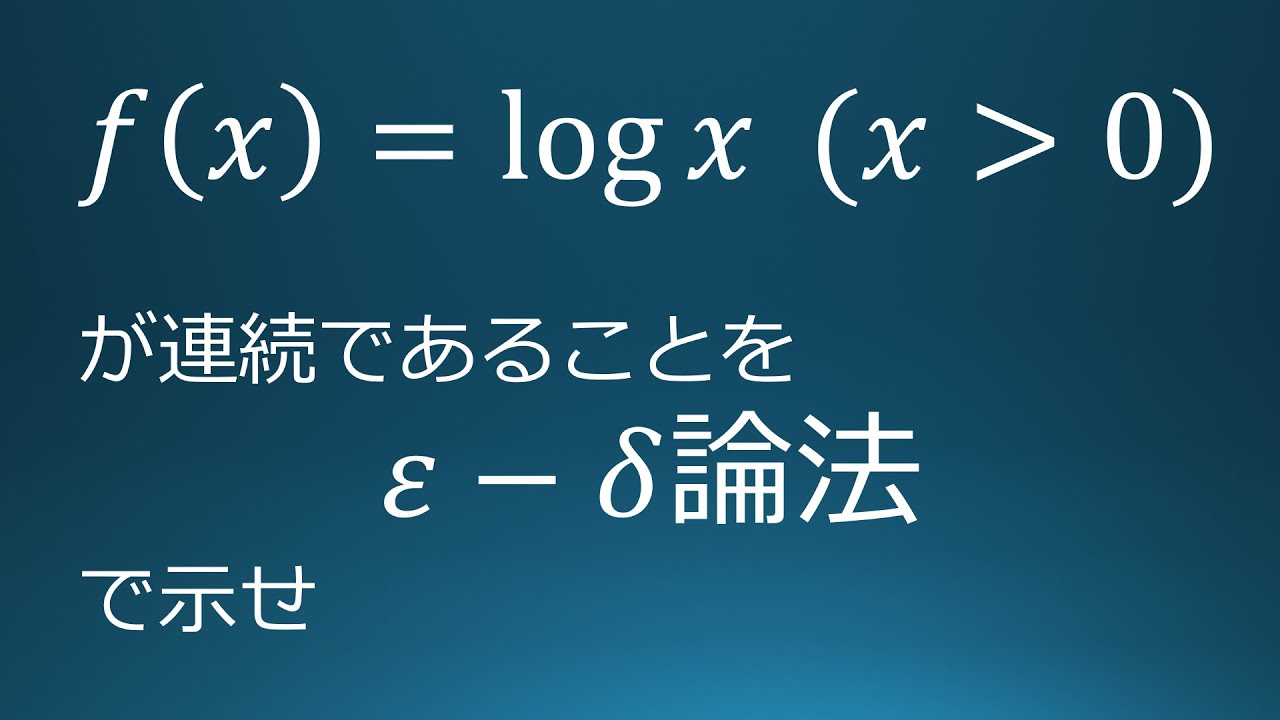
単元：
#数Ⅱ#式と証明#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=\log x\ (x\gt 0)$が連続であることを
$ε-δ$論法で示せ.
この動画を見る
$f(x)=\log x\ (x\gt 0)$が連続であることを
$ε-δ$論法で示せ.
16愛知県教員採用試験（数学：10番（1） 極限値）
単元：
#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{10}$これを解け.
$\displaystyle \lim_{x\to\infty} \ x^2\left(1-\cos \dfrac{1}{x}\right)$
この動画を見る
$\boxed{10}$これを解け.
$\displaystyle \lim_{x\to\infty} \ x^2\left(1-\cos \dfrac{1}{x}\right)$
重積分⑩-5 #151【曲面の面積】（高専数学 微積II，数検1級1次解析対応）
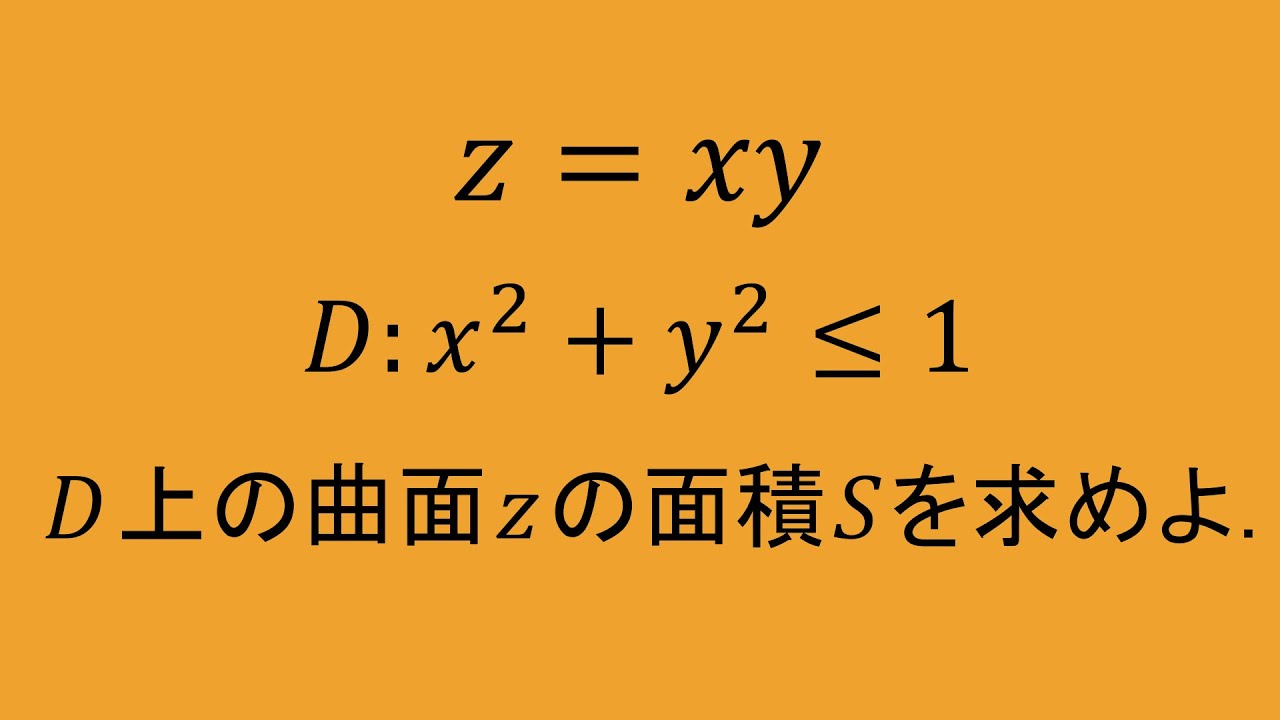
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$D:x^2+y^2\leqq 1$
曲面$Z=xy$の$D$上における面積$S$を求めよ.
この動画を見る
$D:x^2+y^2\leqq 1$
曲面$Z=xy$の$D$上における面積$S$を求めよ.
16愛知県教員採用試験（数学：10番（２） 微分積分）
単元：
#数Ⅱ#微分法と積分法#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{10}$
$f(x)=\displaystyle \int_{0}^{x} \ (1-t^2)e^t \ dt$の極値を求めよ.
この動画を見る
$\boxed{10}$
$f(x)=\displaystyle \int_{0}^{x} \ (1-t^2)e^t \ dt$の極値を求めよ.
ε-δ論法 #1 f(x)=√xが連続
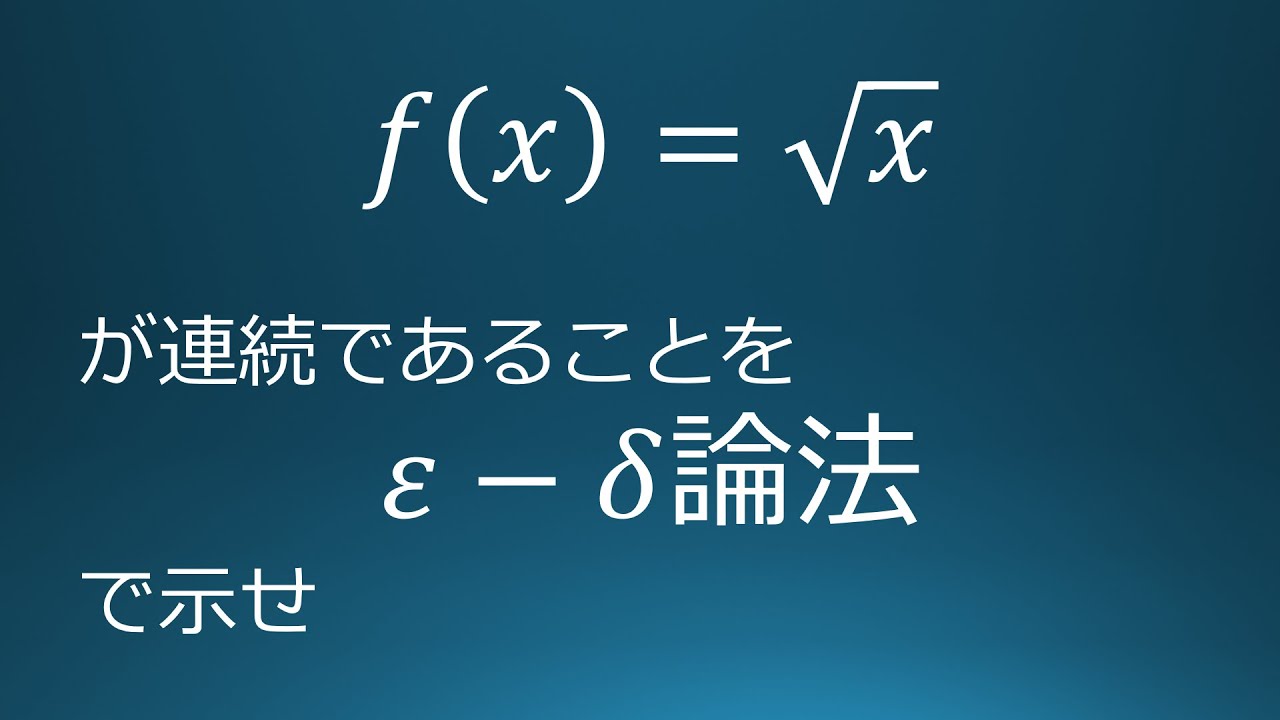
単元：
#数Ⅱ#式と証明#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
Question
$f(x)=\sqrt x\ (x\geqq 0)$が連続であることを$\xi -\vartheta$論法で示せ.
この動画を見る
Question
$f(x)=\sqrt x\ (x\geqq 0)$が連続であることを$\xi -\vartheta$論法で示せ.
重積分⑩-4#150【曲面の面積】（高専数学 微積II，数検1級1次解析対応）
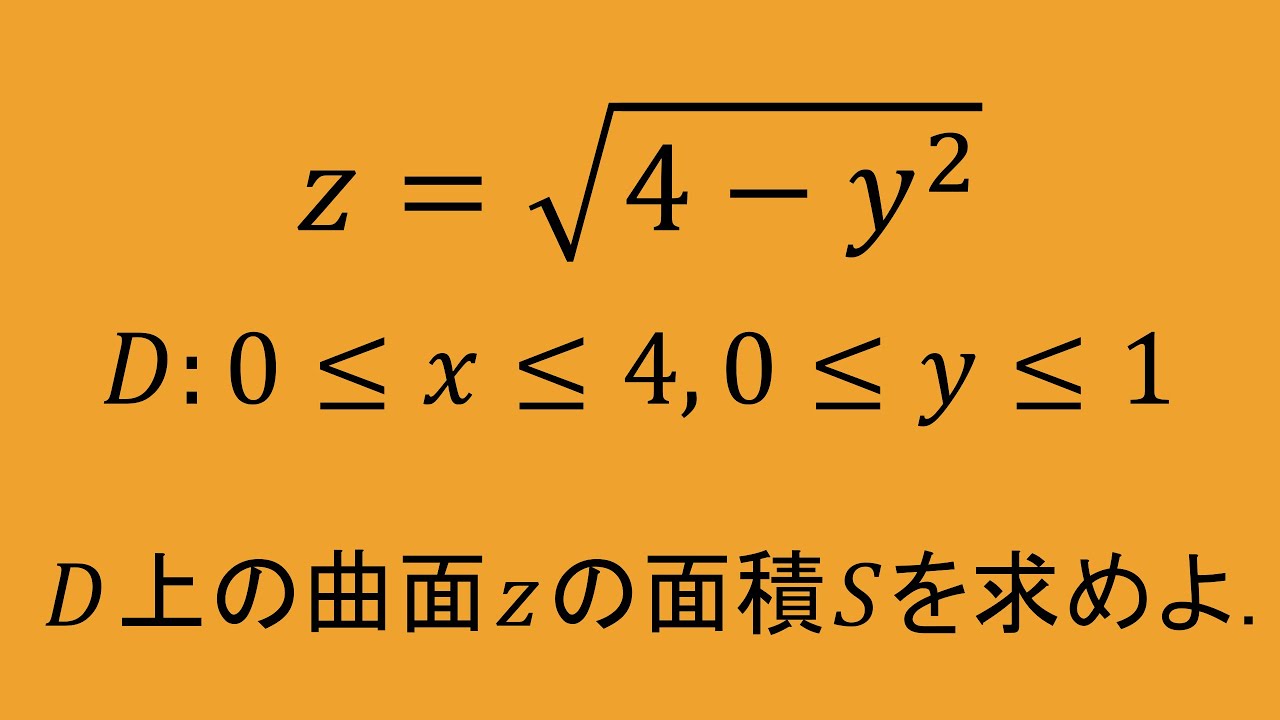
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$D:0\leqq x\leqq 4,0\leqq y\leqq 1$
$D$上における曲面$Z=\sqrt{4-y^2}$の面積$S$を求めよ.
この動画を見る
$D:0\leqq x\leqq 4,0\leqq y\leqq 1$
$D$上における曲面$Z=\sqrt{4-y^2}$の面積$S$を求めよ.
重積分⑨-9#149【広義積分】（高専数学 微積II，数検1級1次解析対応）
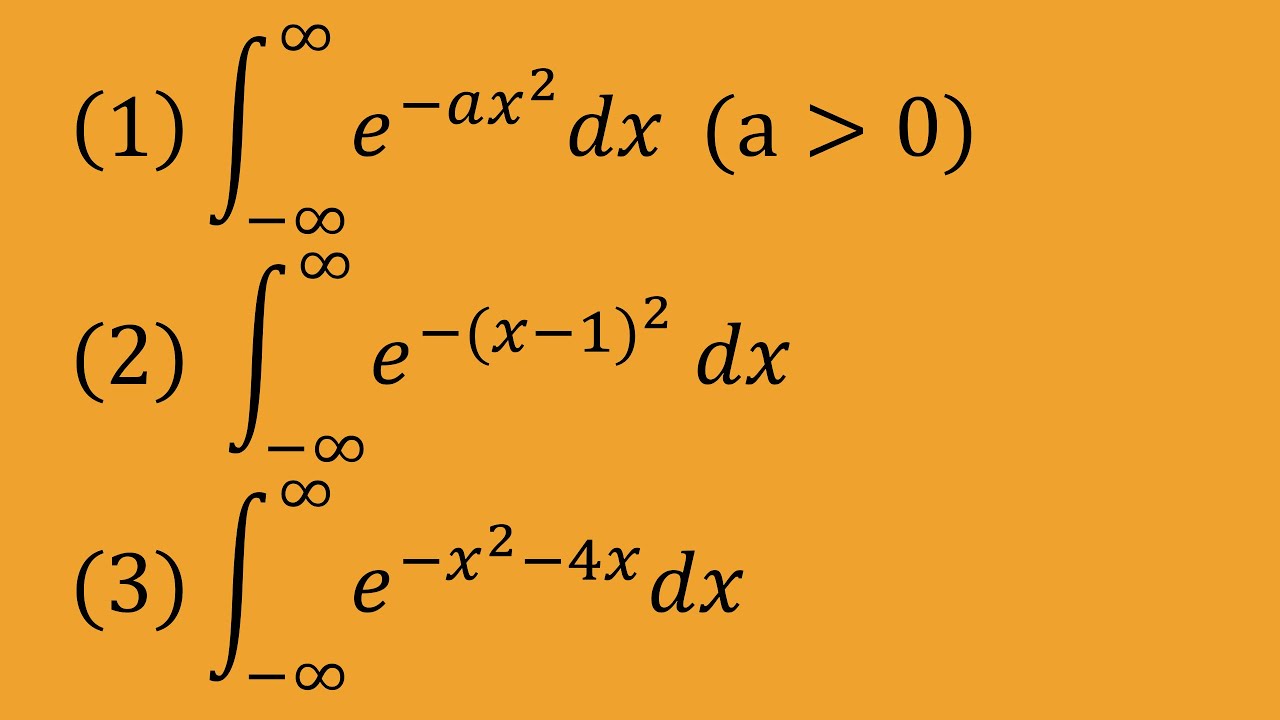
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
これを解け.
(1)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-ax^2} \ dx \ (a\gt 0)$
(2)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-(x-1)^2} \ dx \ $
(3)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-x^2-4x} \ dx \ $
定理$\displaystyle_{0}^{\infty} \ e^{-x^2}\ dx=\dfrac{\sqrt x}{2}$
この動画を見る
これを解け.
(1)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-ax^2} \ dx \ (a\gt 0)$
(2)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-(x-1)^2} \ dx \ $
(3)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-x^2-4x} \ dx \ $
定理$\displaystyle_{0}^{\infty} \ e^{-x^2}\ dx=\dfrac{\sqrt x}{2}$
15愛知県教員採用試験（数学：10番 極限）
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{10}\\ \displaystyle \lim_{x\to 2}\\ \dfrac{\sqrt{2x+a}+b}{x-2}=\dfrac{1}{3}$
$a,b$を求めよ.
この動画を見る
$\boxed{10}\\ \displaystyle \lim_{x\to 2}\\ \dfrac{\sqrt{2x+a}+b}{x-2}=\dfrac{1}{3}$
$a,b$を求めよ.
重積分⑥-4 #146【曲面・平面で囲まれた体積】（高専数学 微積II，数検1級1次解析対応）
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
直円柱$x^2+y^2\leqq 4$
平面$Z=0$,曲面$Z=4-x^2$で囲まれた体積$V$を求めよ.
この動画を見る
直円柱$x^2+y^2\leqq 4$
平面$Z=0$,曲面$Z=4-x^2$で囲まれた体積$V$を求めよ.
重積分⑦-5【極座標による変数変換】（高専数学 微積II，数検1級対応）
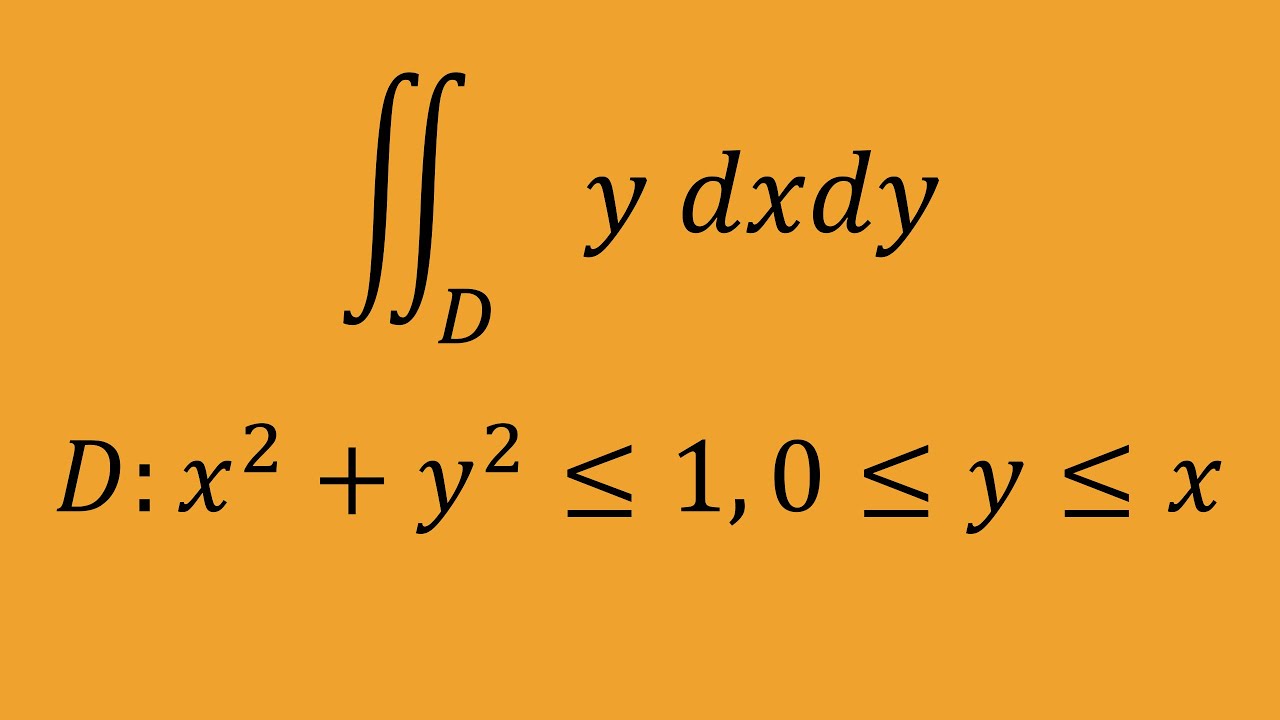
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
これを解け.
$\iint_D\\\ y \ dx \ dy$
$D:x^2+y^2\leqq 1,0\leqq y\leqq x$
この動画を見る
これを解け.
$\iint_D\\\ y \ dx \ dy$
$D:x^2+y^2\leqq 1,0\leqq y\leqq x$
13東京都教員採用試験（数学1-(6) 複素数）
単元：
#数Ⅱ#複素数と方程式#複素数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1} - (6)$
$arg Z=\dfrac{4}{3}\pi,arg(1-Z)=\dfrac{\pi}{4}$のとき,
$arg \dfrac{Z}{(1-Z)^2},\vert Z \vert$を求めよ.
この動画を見る
$\boxed{1} - (6)$
$arg Z=\dfrac{4}{3}\pi,arg(1-Z)=\dfrac{\pi}{4}$のとき,
$arg \dfrac{Z}{(1-Z)^2},\vert Z \vert$を求めよ.
重積分⑧-4【一般の変数変換】（高専数学 微積II，数検1級1次解析対応）
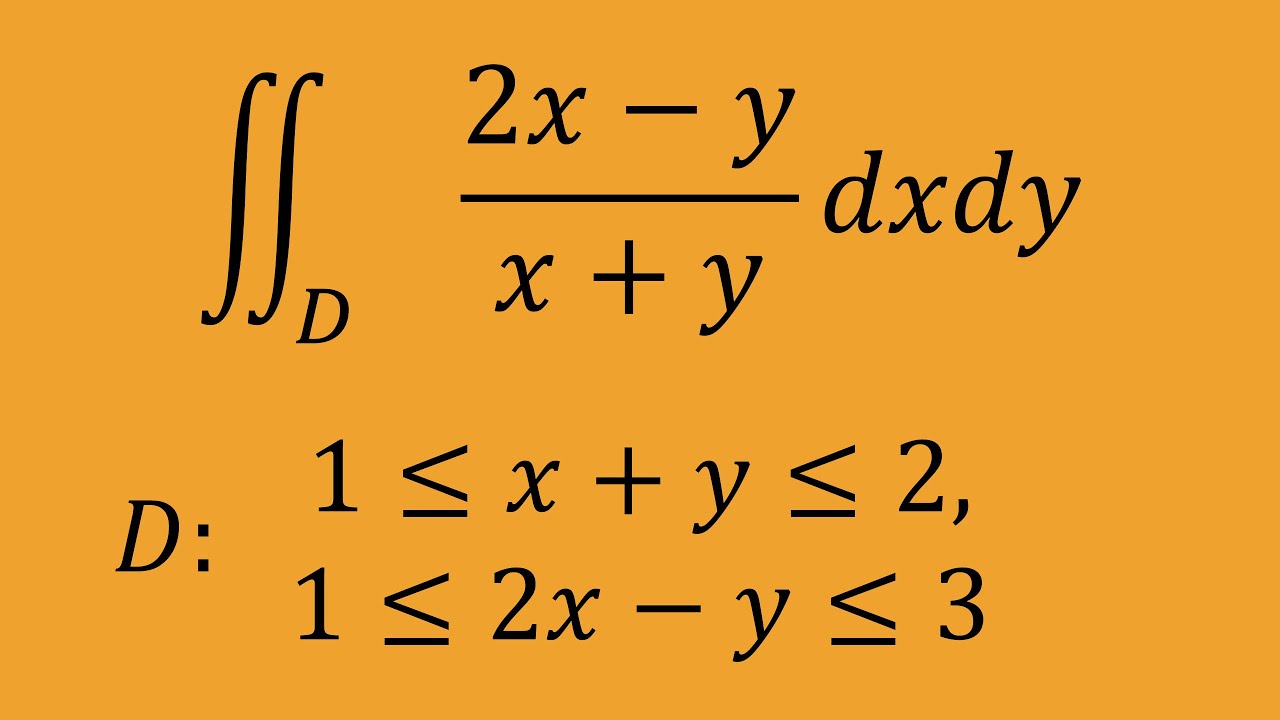
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
これを解け.
$\iint_D \\ \dfrac{2x-y}{x+y}dx\ dy$
$D:1\leqq x+y \leqq 2,1\leqq 2x-y \leqq 3$
この動画を見る
これを解け.
$\iint_D \\ \dfrac{2x-y}{x+y}dx\ dy$
$D:1\leqq x+y \leqq 2,1\leqq 2x-y \leqq 3$
重積分⑨-8【広義積分】（高専数学 微積II，数検1級1次解析対応）
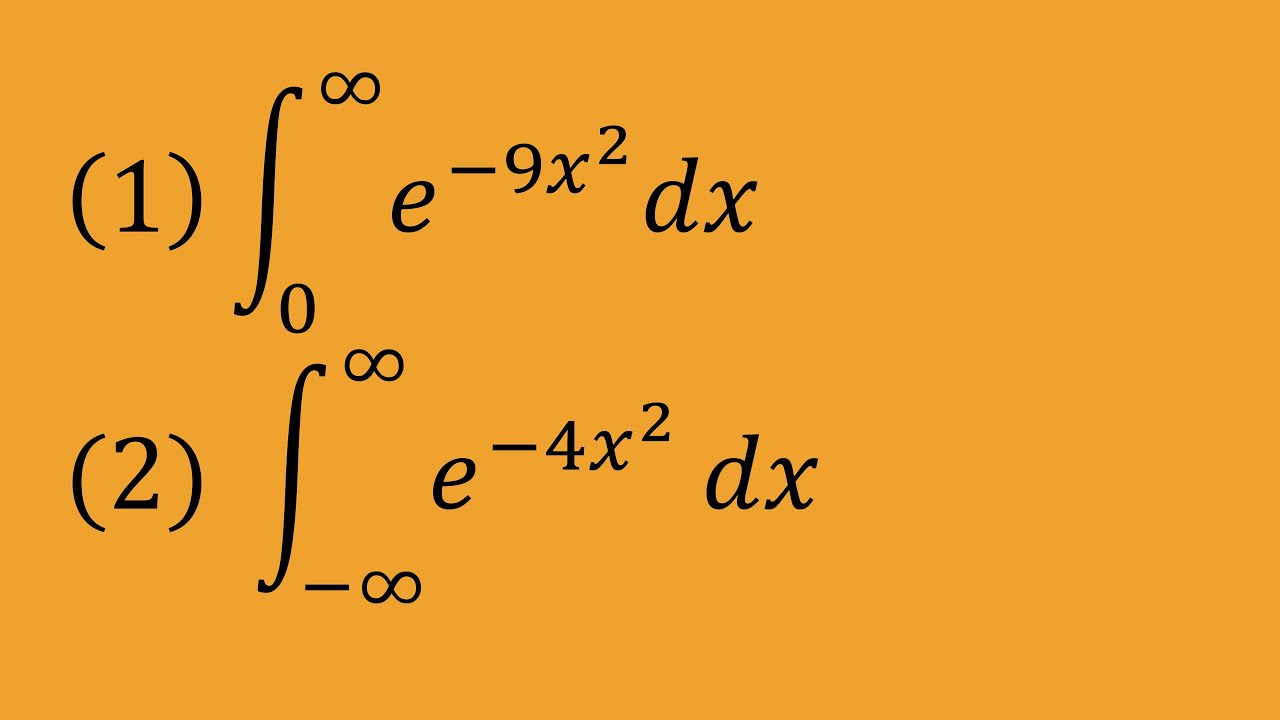
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
これを解け.
(1)$\displaystyle \int_{0}^{\infty} \\ e^{-9x^2}\ dx$
(2)$\displaystyle \int_{-\infty}^{\infty} \\ e^{-4x^2}\ dx$
(3)$\displaystyle \int_{0}^{\infty} \\ e^{-x^2} dx=\dfrac{\sqrt x}{2}$
この動画を見る
これを解け.
(1)$\displaystyle \int_{0}^{\infty} \\ e^{-9x^2}\ dx$
(2)$\displaystyle \int_{-\infty}^{\infty} \\ e^{-4x^2}\ dx$
(3)$\displaystyle \int_{0}^{\infty} \\ e^{-x^2} dx=\dfrac{\sqrt x}{2}$
15東京都教員採用試験（数学1-(5) 数列の和の最小値）
単元：
#数列#数列とその和（等差・等比・階差・Σ）#その他#数学(高校生)#数B#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1} - (5)$
$a_n=n^3-20n$
$S_n$の最小値とそのときの$n$の値を求めよ.
この動画を見る
$\boxed{1} - (5)$
$a_n=n^3-20n$
$S_n$の最小値とそのときの$n$の値を求めよ.
重積分⑨-7【広義積分】（高専数学 微積II，数検1級1次解析対応）
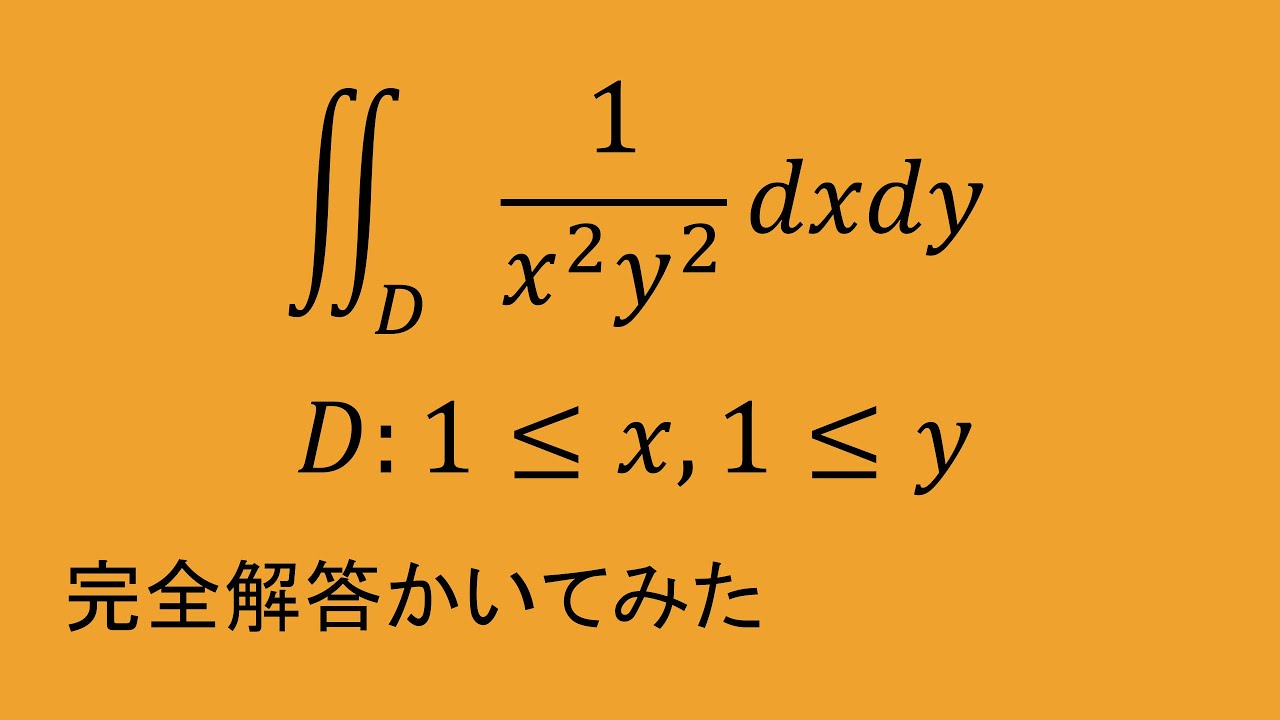
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$D:1\leqq x,1\leqq y$である.
$\iint_D \dfrac{1}{x^2y^2} \ dx \ dy$
これを解け.
この動画を見る
$D:1\leqq x,1\leqq y$である.
$\iint_D \dfrac{1}{x^2y^2} \ dx \ dy$
これを解け.
重積分⑨-6【広義積分】（高専数学 微積II，数検1級1次解析対応）
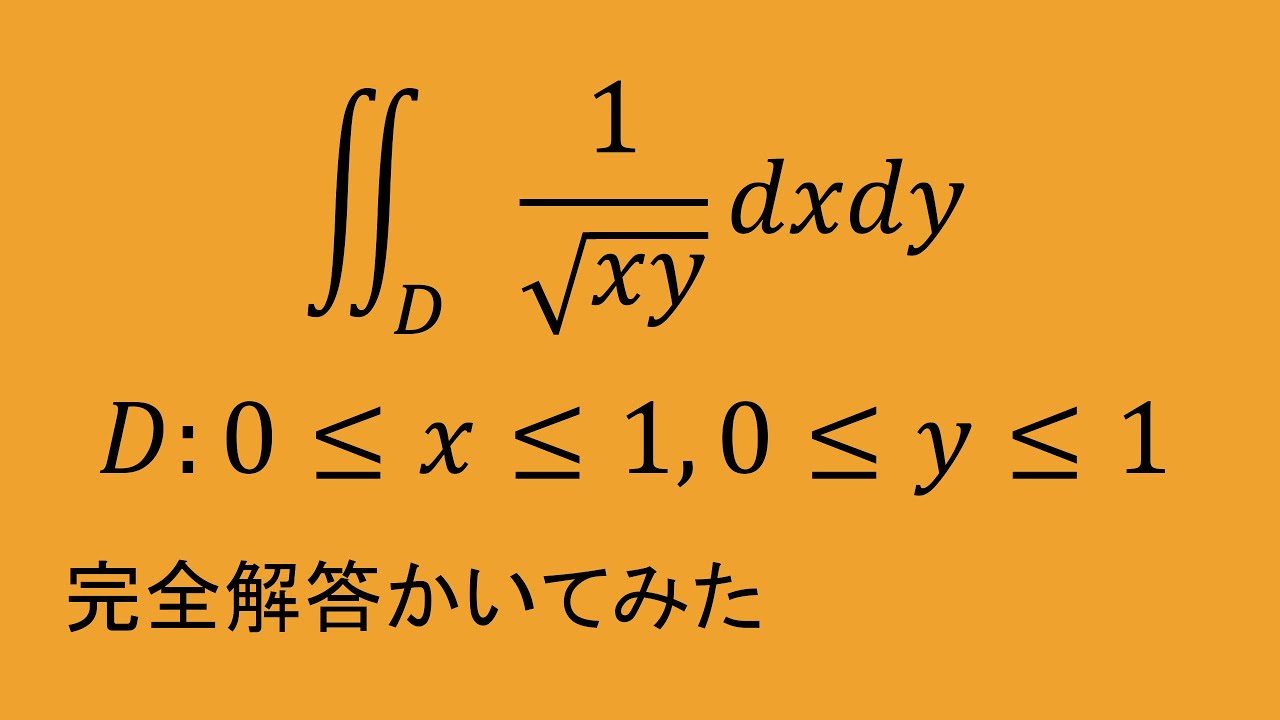
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$D:0\leqq x\leqq 1,0\leqq y\leqq 1$とする.
$\iint_D \ \dfrac{1}{\sqrt{xy}}\ dx \ dy$
これを解け.
この動画を見る
$D:0\leqq x\leqq 1,0\leqq y\leqq 1$とする.
$\iint_D \ \dfrac{1}{\sqrt{xy}}\ dx \ dy$
これを解け.
03兵庫県教員採用試験（数学：3番 三角関数）
単元：
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}$
$0\leqq x\leqq 2\pi$である.
$y=3\sin^2x-2\sin x+\cos^2 x+3$の最大値,最小値と
そのときの$x$の値を求めよ.
この動画を見る
$\boxed{3}$
$0\leqq x\leqq 2\pi$である.
$y=3\sin^2x-2\sin x+\cos^2 x+3$の最大値,最小値と
そのときの$x$の値を求めよ.
#3 数検準1級2次過去問 三角関数
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#数学検定#数学検定準1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}$
$\tan \alpha=k,-\dfrac{\pi}{2}\lt \alpha \lt \dfrac{\pi}{2}$をみたす
$\alpha$を$T(k)$で表す
(1)$xy\neq 1$のとき,
$ \\\ \tan (T(x)+T(y))$
(2)$4T\left(\dfrac{1}{5}\right)-T\left(\dfrac{1}{239}\right)=\dfrac{\pi}{4}$を示せ.
＊$-\dfrac{\pi}{2} \lt \beta\lt \dfrac{\pi}{2}$は利用してよい.
この動画を見る
$\boxed{1}$
$\tan \alpha=k,-\dfrac{\pi}{2}\lt \alpha \lt \dfrac{\pi}{2}$をみたす
$\alpha$を$T(k)$で表す
(1)$xy\neq 1$のとき,
$ \\\ \tan (T(x)+T(y))$
(2)$4T\left(\dfrac{1}{5}\right)-T\left(\dfrac{1}{239}\right)=\dfrac{\pi}{4}$を示せ.
＊$-\dfrac{\pi}{2} \lt \beta\lt \dfrac{\pi}{2}$は利用してよい.
重積分⑥-3【曲面・平面で囲まれた体積】（高専数学 微積II，数検1級1次解析対応）
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a\gt 0$とする.
曲面$Z=4a^2-x^2-y^2$と
$xy$平面で囲まれた体積$V$を求めよ.
この動画を見る
$a\gt 0$とする.
曲面$Z=4a^2-x^2-y^2$と
$xy$平面で囲まれた体積$V$を求めよ.
#2 数検準1級1次過去問 数列
単元：
#数学検定・数学甲子園・数学オリンピック等#数列#数列とその和（等差・等比・階差・Σ）#数学検定#数学検定準1級#数学(高校生)#数B
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{3}$
$2a_n-S_n=2^n$
一般鋼$a_n$を求めよ.
この動画を見る
$\boxed{3}$
$2a_n-S_n=2^n$
一般鋼$a_n$を求めよ.
重積分⑨-5【広義積分】（高専数学 微積II，数検1級1次解析対応）
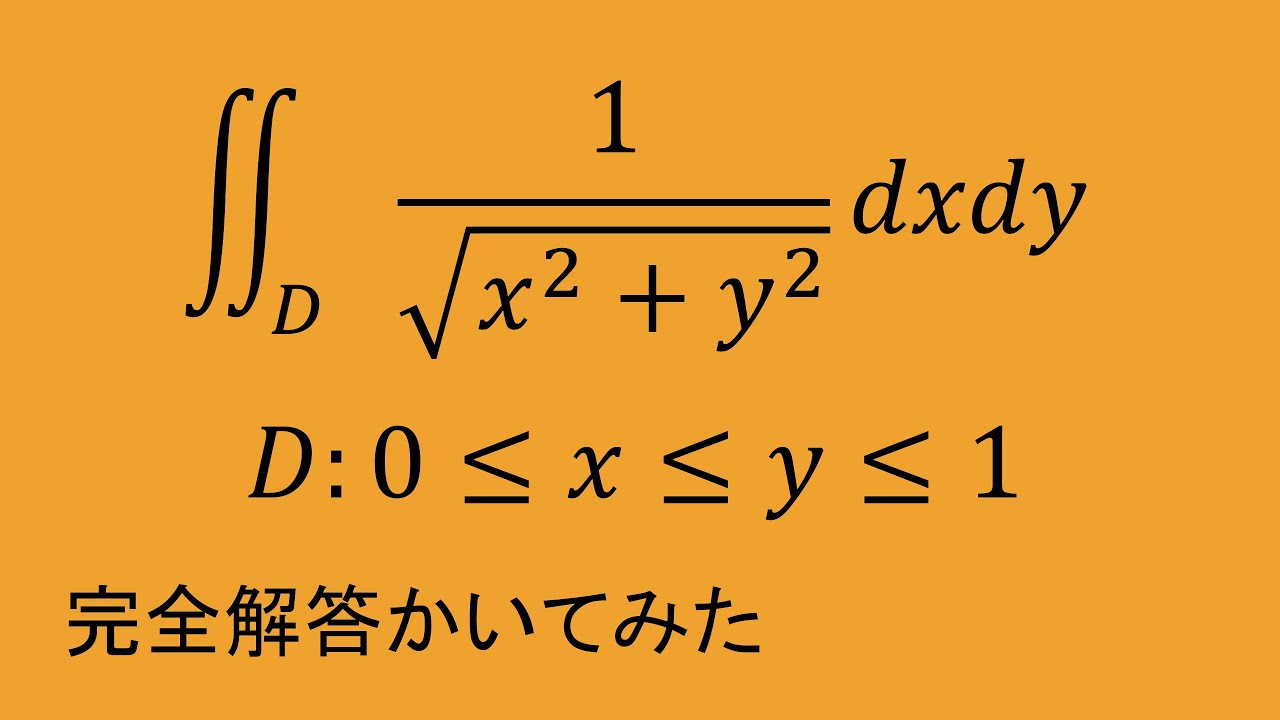
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
これを解け.
$\iint_D \ \dfrac{1}{\sqrt{x^2+y^2}}\ dx \ dy$
$D:0\leqq x\leqq y\leqq 1$
この動画を見る
これを解け.
$\iint_D \ \dfrac{1}{\sqrt{x^2+y^2}}\ dx \ dy$
$D:0\leqq x\leqq y\leqq 1$
#1 数検準1級一次過去問 連立方程式
単元：
#連立方程式#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{1}$これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
3^{x+1}-2・3^y=-9 \\
\log_2 (x+1)-\log_2 (y+2)=-1
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\boxed{1}$これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
3^{x+1}-2・3^y=-9 \\
\log_2 (x+1)-\log_2 (y+2)=-1
\end{array}
\right.
\end{eqnarray}$