 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
Lesson6-3 NT Stage1 3rd Edition【しまだじろうがていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#中1英語#中2英語#文の種類#助動詞#命令文、否定の命令文、ていねいな命令文、Let's~.の文、あいさつ#canの文(肯定文・否定文・疑問文)#can、could、be able to、may、must、have to、should、助動詞を使った表現#命令文、Let's~、Don't~、命令文, and(or)~の文
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson6#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson6-1のcanの肯定文と否定文の復習から行い、
今回Lesson6-2の内容である、
・canの疑問文
・canの疑問文の注意点(can youの使い方)
・canの疑問詞疑問文
・be動詞の命令文
・be動詞の否定の命令文
をていねいに教えます!
この動画を見る
Lesson6-1のcanの肯定文と否定文の復習から行い、
今回Lesson6-2の内容である、
・canの疑問文
・canの疑問文の注意点(can youの使い方)
・canの疑問詞疑問文
・be動詞の命令文
・be動詞の否定の命令文
をていねいに教えます!
Lesson6-3 ニュートレジャー Stage1 3rd Edition【しまだじろうがていねいに解説】

単元:
#英語(中学生)#中1英語#canの文(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson6-1のcanの肯定文と否定文の復習から行い、
今回Lesson6-2の内容である、
・canの疑問文
・canの疑問文の注意点(can youの使い方)
・canの疑問詞疑問文
・be動詞の命令文
・be動詞の否定の命令文
をていねいに教えます!
この動画を見る
Lesson6-1のcanの肯定文と否定文の復習から行い、
今回Lesson6-2の内容である、
・canの疑問文
・canの疑問文の注意点(can youの使い方)
・canの疑問詞疑問文
・be動詞の命令文
・be動詞の否定の命令文
をていねいに教えます!
図形と計量 三角比の相互関係の利用2 【NI・SHI・NOがていねいに解説】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\sin^4\theta-\cos^4\theta$を$\sin\theta$だけを用いた式で表せ。また,$\cos\theta$だけを用いた式で表せ。
この動画を見る
$\sin^4\theta-\cos^4\theta$を$\sin\theta$だけを用いた式で表せ。また,$\cos\theta$だけを用いた式で表せ。
図形と計量 三角比の相互関係の利用【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
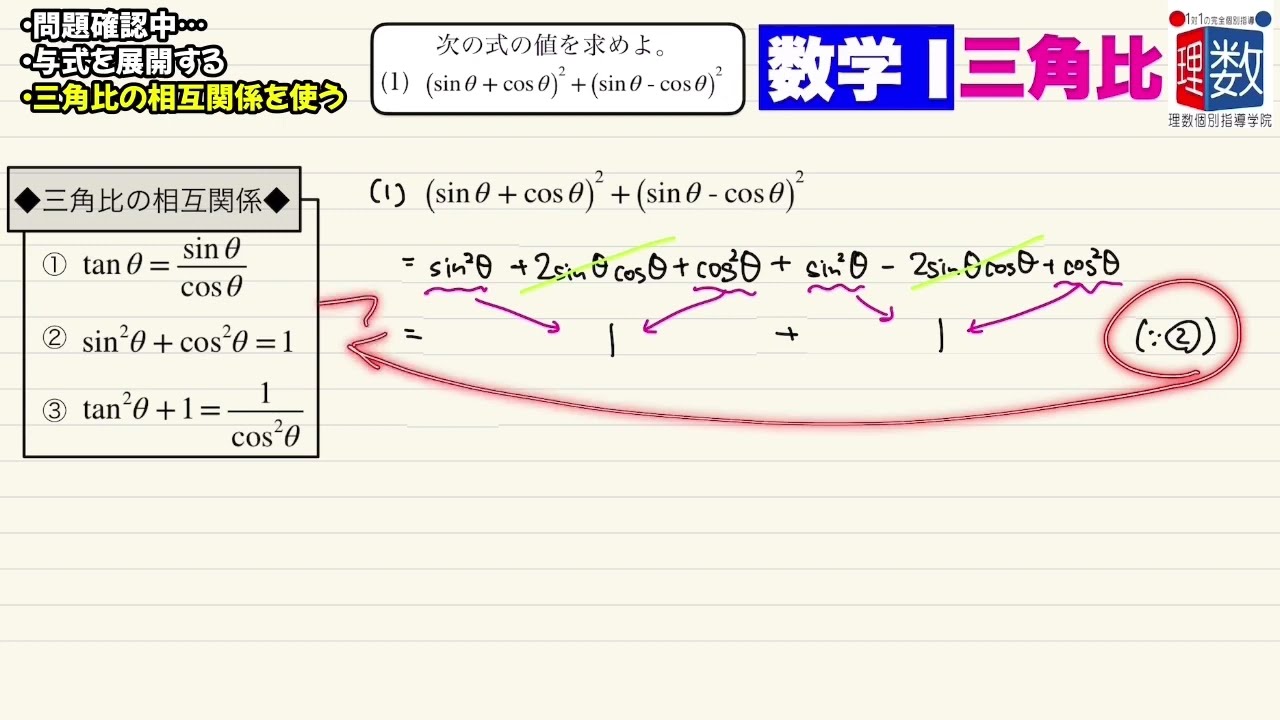
次の式の値を求めよ。
(1)$(\sin\theta+\cos\theta)^2+(\sin\theta-\cos\theta)^2$
(2)$(1-\sin\theta)(1+\sin\theta)-\dfrac{1}{1+\tan^2\theta}$
この動画を見る
次の式の値を求めよ。
(1)$(\sin\theta+\cos\theta)^2+(\sin\theta-\cos\theta)^2$
(2)$(1-\sin\theta)(1+\sin\theta)-\dfrac{1}{1+\tan^2\theta}$
図形と計量 有名角以外を含む三角比計算【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
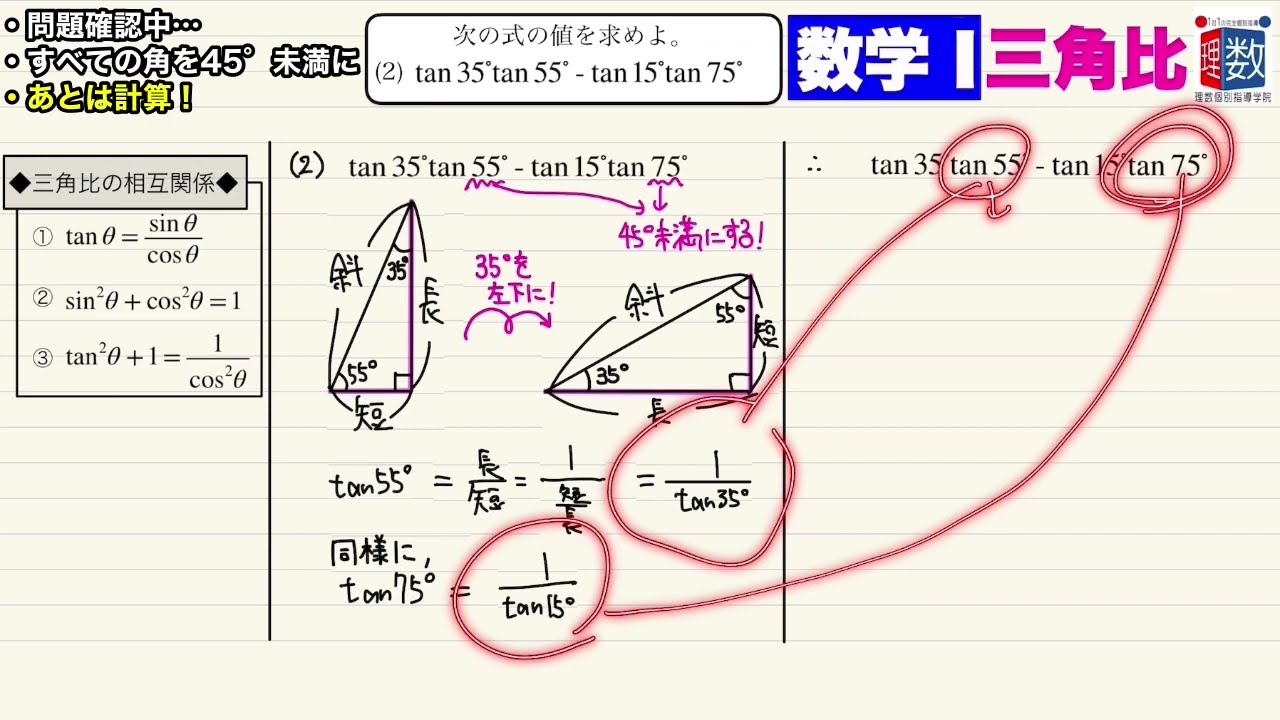
次の式の値を求めよ。
(1) $\sin^240°+\sin^250°$
(2) $\tan35°\tan55°+\tan15°\tan75°$
(3) $(\sin70°+\sin20°)^2-2\tan70°\cos^250°$
この動画を見る
次の式の値を求めよ。
(1) $\sin^240°+\sin^250°$
(2) $\tan35°\tan55°+\tan15°\tan75°$
(3) $(\sin70°+\sin20°)^2-2\tan70°\cos^250°$
【受験算数】年齢算:現在、父は42才、子どもは8才です。父の年齢が子どもの年齢の3倍になるのは何年後ですか。

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
理数個別チャンネル
問題文全文(内容文):
現在、父は42才、子どもは8才です。父の年齢が子どもの年齢の3倍になるのは何年後ですか。
この動画を見る
現在、父は42才、子どもは8才です。父の年齢が子どもの年齢の3倍になるのは何年後ですか。
【受験算数】和差算:姉と妹は合わせて1500円使いました。姉が300円多く使ったとき、姉は何円使いましたか。

単元:
#算数(中学受験)#文章題#和差算・植木算・分配算・倍数算・年齢算・相当算・つるかめ算
指導講師:
理数個別チャンネル
問題文全文(内容文):
姉と妹は合わせて1500円使いました。姉が300円多く使ったとき、姉は何円使いましたか。
この動画を見る
姉と妹は合わせて1500円使いました。姉が300円多く使ったとき、姉は何円使いましたか。
Lesson4-2 NT Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中1英語#形容詞・副詞#一般動詞(3人称・単数)(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson4#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
3単現の否定文、疑問文
この動画を見る
3単現の否定文、疑問文
Lesson4-2 ニュートレジャー Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中1英語#一般動詞(3人称・単数)(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
3単現の否定文、疑問文に関して解説していきます.
この動画を見る
3単現の否定文、疑問文に関して解説していきます.
【英検・IELTS・大学受験英作文】意見と理由を書くライティングで使える10の言い換えフレーズ

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#英検準1級
指導講師:
理数個別チャンネル
問題文全文(内容文):
「英検準1級・2級のライティング」を基礎から9割得点まで引き上げる全6編の完全版です。
英検合格にお役立てできれば嬉しいです。
この動画を見る
「英検準1級・2級のライティング」を基礎から9割得点まで引き上げる全6編の完全版です。
英検合格にお役立てできれば嬉しいです。
【英検準1級・2級ライティング】⑤本番ですぐに使える言い換え表現/英作文フレーズ集

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英検2級#英検準1級
指導講師:
理数個別チャンネル
問題文全文(内容文):
「英検準1級・2級のライティング」を基礎から9割得点まで引き上げる全6編の完全版です。
英検合格にお役立てできれば嬉しいです。
この動画を見る
「英検準1級・2級のライティング」を基礎から9割得点まで引き上げる全6編の完全版です。
英検合格にお役立てできれば嬉しいです。
【英検・IELTS・大学受験英作文】意見と理由を書くライティングで使える10の言い換えフレーズ【期間限定で無料pdf配布中】

単元:
#英検・TOEIC・IELTS・TOEFL・IELTS等#英検#英語リスニング・スピーキング#スピーキング#英検
指導講師:
理数個別チャンネル
問題文全文(内容文):
意見と理由を書くライティングで使える10の言い換えフレーズを解説していきます.
この動画を見る
意見と理由を書くライティングで使える10の言い換えフレーズを解説していきます.
【数検準2級】高校数学:数学検定準2級2次:問7

単元:
#数学検定・数学甲子園・数学オリンピック等#その他#数学検定#数学検定準2級#その他#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問7. 次の問いに答えなさい。
(10) さきこさんとゆうたさんは、次のような数当てゲームをしています。
① さきこさんは、4桁の数を決めて紙に書く。ただし、どの位の数字も異なり、0は含まないものとする。
② ゆうたさんは、さきこさんが書いた4桁の数を予想して伝える。
③ さきこさんは、ゆうたさんが予想した4桁の数で、位と数字も当たっている数字の個数と、位は違うが数字が当たっている数字の
個数をヒントとして伝える。
④ ゆうたさんは、さきこさんのヒントをもとに、再び数を予想する。
ゆうたさんは6回めの予想で、さきこさんが書いた4桁の数を当てました。下の表は、ゆうたさんが5回めまでに予想した数を、それに対するさきこ
さんのヒントです。
このとき、さきこさんが書いた4桁の数を求めなさい。この問題は答えだけを書いてください。
この動画を見る
問7. 次の問いに答えなさい。
(10) さきこさんとゆうたさんは、次のような数当てゲームをしています。
① さきこさんは、4桁の数を決めて紙に書く。ただし、どの位の数字も異なり、0は含まないものとする。
② ゆうたさんは、さきこさんが書いた4桁の数を予想して伝える。
③ さきこさんは、ゆうたさんが予想した4桁の数で、位と数字も当たっている数字の個数と、位は違うが数字が当たっている数字の
個数をヒントとして伝える。
④ ゆうたさんは、さきこさんのヒントをもとに、再び数を予想する。
ゆうたさんは6回めの予想で、さきこさんが書いた4桁の数を当てました。下の表は、ゆうたさんが5回めまでに予想した数を、それに対するさきこ
さんのヒントです。
このとき、さきこさんが書いた4桁の数を求めなさい。この問題は答えだけを書いてください。
【数検準2級】高校数学:数学検定準2級2次:問6

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#場合の数と確率#確率#数学検定#数学検定準2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問6. AチームとBチームが野球の試合を行います。どの試合も、AチームがBチームに勝つ確率は1/3で、引き分けはないものとします。
これについて、次の問いに答えなさい。
(8) 3試合めまで終えた時点でAチームが3勝0敗となる確率を求めなさい。この問題は答えだけを書いてください。
(9) 5試合めまで終えた時点でAチームが3勝2敗となる確率を求めなさい。
この動画を見る
問6. AチームとBチームが野球の試合を行います。どの試合も、AチームがBチームに勝つ確率は1/3で、引き分けはないものとします。
これについて、次の問いに答えなさい。
(8) 3試合めまで終えた時点でAチームが3勝0敗となる確率を求めなさい。この問題は答えだけを書いてください。
(9) 5試合めまで終えた時点でAチームが3勝2敗となる確率を求めなさい。
【数検準2級】高校数学:数学検定準2級2次:問5

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学検定#数学検定準2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問5. 次の問いに答えなさい。
(7) 地点Aから、湖を隔てた地点Bまでの距離を測定するために、地点Aから100m、地点Bから60m離れたところに地点Pをとります。地点Pから地点A、Bをみて$\angle APB$の大きさを調べたところ、$\angle APB=120°$でした。
このとき、2地点A、B間の距離は何mですか。余弦定理を用いて求めなさい。
この動画を見る
問5. 次の問いに答えなさい。
(7) 地点Aから、湖を隔てた地点Bまでの距離を測定するために、地点Aから100m、地点Bから60m離れたところに地点Pをとります。地点Pから地点A、Bをみて$\angle APB$の大きさを調べたところ、$\angle APB=120°$でした。
このとき、2地点A、B間の距離は何mですか。余弦定理を用いて求めなさい。
場合の数 並び替え基本【セトリの算数がていねいに解説】

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・6個の数字1,2,3,4,5,6から異なる4種の数字を使って4桁の整数を作るとき、次のような整数は何個あるか。
(1)4300より大きい整数
(2)5000より大きい整数
・女子5人、男子3人が1列に並ぶとき、次の並び方は何通りあるか。
(1)女子5人が続いて並ぶ。
(2)女子5人、男子3人がそれぞれ続いて並ぶ。
(3)両端が男子である。
(4)どの男子も隣合わない。
・男子4人、女子4人が男女交互に1列に並ぶ方法は何通りあるか。
この動画を見る
・6個の数字1,2,3,4,5,6から異なる4種の数字を使って4桁の整数を作るとき、次のような整数は何個あるか。
(1)4300より大きい整数
(2)5000より大きい整数
・女子5人、男子3人が1列に並ぶとき、次の並び方は何通りあるか。
(1)女子5人が続いて並ぶ。
(2)女子5人、男子3人がそれぞれ続いて並ぶ。
(3)両端が男子である。
(4)どの男子も隣合わない。
・男子4人、女子4人が男女交互に1列に並ぶ方法は何通りあるか。
場合の数 組み合わせ考え方の基本1 【セトリの算数がていねいに解説】

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
・5人乗りの車に5人が乗車してドライブをするとき、乗り方は何通りあるか。次の各場合について求めよ。
(1)5人全員が運転免許を持っている場合
(2)5人のうち3人だけが運転免許を持っている場合
・6個の数字0,1,2,3,4,5を使ってできる、次のような整数は何個あるか。ただし、同じ数字は2度以上使わないこととする。
(1)6桁の整数
(2)6桁の整数で5の倍数
・5個の数字0,1,2,3,4を使ってできる3桁の整数のうち、次のような整数は何個あるか。ただし、同じ数字は2度以上使わないものとする。
(1)偶数
(2)3の倍数
この動画を見る
・5人乗りの車に5人が乗車してドライブをするとき、乗り方は何通りあるか。次の各場合について求めよ。
(1)5人全員が運転免許を持っている場合
(2)5人のうち3人だけが運転免許を持っている場合
・6個の数字0,1,2,3,4,5を使ってできる、次のような整数は何個あるか。ただし、同じ数字は2度以上使わないこととする。
(1)6桁の整数
(2)6桁の整数で5の倍数
・5個の数字0,1,2,3,4を使ってできる3桁の整数のうち、次のような整数は何個あるか。ただし、同じ数字は2度以上使わないものとする。
(1)偶数
(2)3の倍数
Lesson2-2 NT Stage2 3rd Edition【まどか's Englishがていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#品詞と文型、句と節#中2英語#接続詞#接続詞(and,or,but,so・when,if,because,before,after・接続詞that)
教材:
#NT ENGLISH SERIES#Third Edition Stage2#Lesson2#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
接続詞thatと時制の一致について確認します!
この動画を見る
接続詞thatと時制の一致について確認します!
Lesson2-2 ニュートレジャー Stage2 3rd Edition【まどか's Englishがていねいに解説】

単元:
#英語(中学生)#中2英語#接続詞(and,or,but,so・when,if,because,before,after・接続詞that)
指導講師:
理数個別チャンネル
問題文全文(内容文):
接続詞thatと時制の一致について確認します!
この動画を見る
接続詞thatと時制の一致について確認します!
Lesson5-3 NT Stage1 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中1英語#Where、Which、Howで始まる疑問文
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson5#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T.のLesson5-3の解説です。
この動画を見る
N.T.のLesson5-3の解説です。
Lesson5-3 ニュートレジャー Stage1 3rd Edition【YAKISOBA先生がていねいに解説】

単元:
#英語(中学生)#中1英語#This is~. That is~. What is~? の文(肯定文・否定文・疑問文)#He(She) is~. Who is~?の文(肯定文・否定文・疑問文)#代名詞の目的格、所有代名詞、Whose~?と答え方#Where、Which、Howで始まる疑問文
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage1 3rd EditionのLesson5-3の解説です。
この動画を見る
ニュートレジャー Stage1 3rd EditionのLesson5-3の解説です。
場合の数 集合~ベン図にまとめよう~【さこすけ's サイエンスがていねいに解説】

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある地区で、新聞Aを購読している世帯は全体の50%、新聞Bを購読して
いる世帯は全体の60%、両方を購読している世帯は全体の30%、どちら
も購読していない世帯は8世帯であった。このとき、Aだけを購読している
世帯は全体の何%か。また、この地区の世帯数を求めよ。
海外旅行者100人のうち、75人がカゼ薬を、80人が胃薬を携帯して
いた。次のような人は、最も多くて何人か。また少なくて何人か。
(1)カゼ薬と胃薬を両方とも携帯した人
(2)カゼ薬と胃薬を両方とも携帯してない人
この動画を見る
ある地区で、新聞Aを購読している世帯は全体の50%、新聞Bを購読して
いる世帯は全体の60%、両方を購読している世帯は全体の30%、どちら
も購読していない世帯は8世帯であった。このとき、Aだけを購読している
世帯は全体の何%か。また、この地区の世帯数を求めよ。
海外旅行者100人のうち、75人がカゼ薬を、80人が胃薬を携帯して
いた。次のような人は、最も多くて何人か。また少なくて何人か。
(1)カゼ薬と胃薬を両方とも携帯した人
(2)カゼ薬と胃薬を両方とも携帯してない人
Lesson1-2 NT Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中1英語#This is~. That is~. What is~? の文(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson1#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
this that の文、使い方
この動画を見る
this that の文、使い方
Lesson1-2 ニュートレジャー Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中1英語#中2英語#This is~. That is~. What is~? の文(肯定文・否定文・疑問文)#be動詞の過去形(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
this that の文、使い方に関して解説していきます.
この動画を見る
this that の文、使い方に関して解説していきます.
Lesson4-1 ニュートレジャー Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中1英語#一般動詞(1・2人称)(肯定文・否定文・疑問文)#一般動詞(3人称・単数)(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
一般動詞の文を解説します
この動画を見る
一般動詞の文を解説します
Lesson4-1 NT Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中1英語#一般動詞(3人称・単数)(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson4#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
一般動詞の文を解説します
この動画を見る
一般動詞の文を解説します
Lesson8-1 NT Stage1 3rd Edition【シュン・ヒノハラがていねいに解説】

単元:
#英語(中学生)#中2英語#規則動詞の過去形(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson8#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
今回は一般動詞の過去形(規則動詞)について解説しています。
この動画を見る
今回は一般動詞の過去形(規則動詞)について解説しています。
Lesson8-3 NT Stage1 3rd Edition【シュン・ヒノハラがていねいに解説】

単元:
#英語(中学生)#中2英語#不規則動詞の過去形(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson8#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
今回はLesson8-3 一般動詞の過去形(不規則動詞)についての解説です。
この動画を見る
今回はLesson8-3 一般動詞の過去形(不規則動詞)についての解説です。
Lesson8-3 ニュートレジャー Stage1 3rd Edition【シュン・ヒノハラがていねいに解説】

単元:
#英語(中学生)#中2英語#不規則動詞の過去形(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
今回はLesson8-3 一般動詞の過去形(不規則動詞)についての解説です。
この動画を見る
今回はLesson8-3 一般動詞の過去形(不規則動詞)についての解説です。
Lesson8-1 ニュートレジャー Stage1 3rd Edition【シュン・ヒノハラがていねいに解説】

単元:
#英語(中学生)#中2英語#規則動詞の過去形(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
今回は一般動詞の過去形(規則動詞)について解説しています。
この動画を見る
今回は一般動詞の過去形(規則動詞)について解説しています。




