 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
データの分析 平均点からデータを求める【ユースケ・マセマティックがていねいに解説】

単元:
#数Ⅰ#データの分析#データの分析#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のデータは、ある体操競技会に参加した10人のある種目の得点である。
13.2 13.0 13.7 12.5 14.6 12.3 12.5 11.9 13.9 a (単位は点)
このデータの平均値が13.1点であるとき、aの値を求めよ。
この動画を見る
次のデータは、ある体操競技会に参加した10人のある種目の得点である。
13.2 13.0 13.7 12.5 14.6 12.3 12.5 11.9 13.9 a (単位は点)
このデータの平均値が13.1点であるとき、aの値を求めよ。
数と式 1次不等式の利用【ホーン・フィールドがていねいに解説】

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のものを求めよ。
(1)不等式$5(x-3)\lt -2(x-14)$を満たす最大の整数x
(2)不等式$\dfrac{x}{2}+\dfrac{4}{3}\geqq x-\dfrac{2}{3}$を満たす自然数xの個数
不等式$2x-3gt a+8x$について、次の問いに答えよ。
(1)解が$x\lt 1$となるように、定数aの値を定めよ。
(2)解が$x=0$を含むように、定数aの値の範囲を定めよ。
(3)この不等式を満たすxのうち、最大の整数が0となるように、定数aの値の範囲を定めよ。
aを定数とするとき、次の方程式、不等式を解け。
(1)$ax=1$
(2)$ax\leqq 2$
(3)$ax+6\gt 3x+2a$
この動画を見る
次のものを求めよ。
(1)不等式$5(x-3)\lt -2(x-14)$を満たす最大の整数x
(2)不等式$\dfrac{x}{2}+\dfrac{4}{3}\geqq x-\dfrac{2}{3}$を満たす自然数xの個数
不等式$2x-3gt a+8x$について、次の問いに答えよ。
(1)解が$x\lt 1$となるように、定数aの値を定めよ。
(2)解が$x=0$を含むように、定数aの値の範囲を定めよ。
(3)この不等式を満たすxのうち、最大の整数が0となるように、定数aの値の範囲を定めよ。
aを定数とするとき、次の方程式、不等式を解け。
(1)$ax=1$
(2)$ax\leqq 2$
(3)$ax+6\gt 3x+2a$
整数の性質 最小公倍数、最大公約数の基本① 【ゆう☆たろうがていねいに解説】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
nは正の整数とする。次のようなnをすべて求めよ。
(1)nと36の最小公倍数が504
(2)nと48の最小公倍数が720
3つの自然数40,56,nの最大公約数が8,最小公倍数が1400であるとき,nをすべて求めよ。
aは自然数とする。a+2は6の倍数であり,a+6は8の倍数であるとき,a+14は24の倍数であることを証明せよ
この動画を見る
nは正の整数とする。次のようなnをすべて求めよ。
(1)nと36の最小公倍数が504
(2)nと48の最小公倍数が720
3つの自然数40,56,nの最大公約数が8,最小公倍数が1400であるとき,nをすべて求めよ。
aは自然数とする。a+2は6の倍数であり,a+6は8の倍数であるとき,a+14は24の倍数であることを証明せよ
図形の性質 図形の性質の基本②【中学受験のドラえもんがていねいに解説】
単元:
#数A#図形の性質#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形ABCの内心をIとし、3辺BC、CA、ABに関してIと対称な点をそれぞれP,Q,Rとする。Iは三角形PQRについてどのような点か?
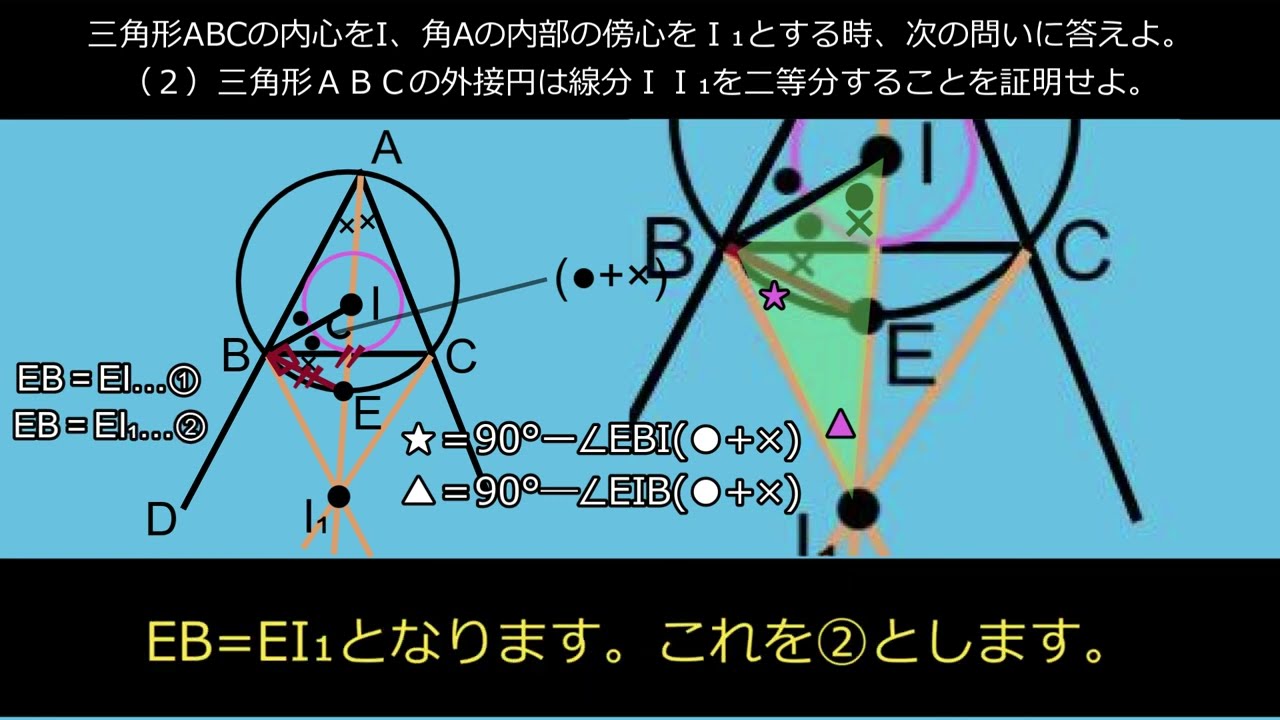
三角形ABCの内心をI、角Aの内部の傍心をI₁とする時、次の問いに答えよ。
(1)角IBI₁の大きさを求めよ。
(2)三角形ABCの外接円は線分II₁を二等分することを証明せよ。
AB=ACである二等辺三角形ABCの頂点Aから辺BCに下ろした垂線をADとする。
角Bの内部の傍接円IBの半径はADに等しいことを証明せよ。
この動画を見る
三角形ABCの内心をIとし、3辺BC、CA、ABに関してIと対称な点をそれぞれP,Q,Rとする。Iは三角形PQRについてどのような点か?
三角形ABCの内心をI、角Aの内部の傍心をI₁とする時、次の問いに答えよ。
(1)角IBI₁の大きさを求めよ。
(2)三角形ABCの外接円は線分II₁を二等分することを証明せよ。
AB=ACである二等辺三角形ABCの頂点Aから辺BCに下ろした垂線をADとする。
角Bの内部の傍接円IBの半径はADに等しいことを証明せよ。
場合の数 集合の個数~ベン図も使えます~【さこすけ's サイエンスがていねいに解説】
単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
全体集合Uと,その部分集合A,Bに対して$n(U)=50,n(A∪B)=42,n(A∩B)=3,
n$($A$の補集合$∩B)=15$であるとき、次の集合の要素の個数を求めよ。
(1)$A$の補集合$∩B$の補集合 (2)$A∩B$の補集合 (3)$A$
500以上1000以下の整数のうち,次のような数は何個あるか。
(1)11の倍数でない整数 (2)11の倍数であるが3の倍数でない整数
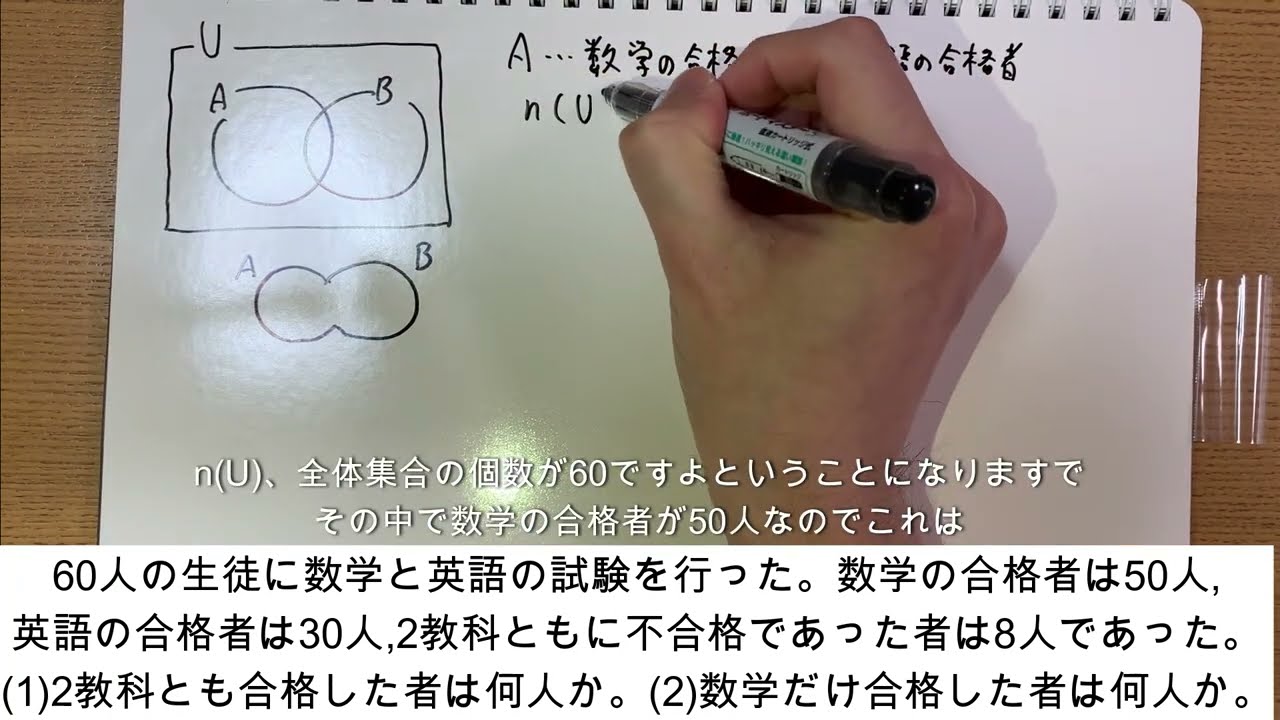
60人の生徒に数学と英語の試験を行った。数学の合格者は50人,
英語の合格者は30人,2教科ともに不合格であった者は8人であった。
(1)2教科とも合格した者は何人か。(2)数学だけ合格した者は何人か。
この動画を見る
全体集合Uと,その部分集合A,Bに対して$n(U)=50,n(A∪B)=42,n(A∩B)=3,
n$($A$の補集合$∩B)=15$であるとき、次の集合の要素の個数を求めよ。
(1)$A$の補集合$∩B$の補集合 (2)$A∩B$の補集合 (3)$A$
500以上1000以下の整数のうち,次のような数は何個あるか。
(1)11の倍数でない整数 (2)11の倍数であるが3の倍数でない整数
60人の生徒に数学と英語の試験を行った。数学の合格者は50人,
英語の合格者は30人,2教科ともに不合格であった者は8人であった。
(1)2教科とも合格した者は何人か。(2)数学だけ合格した者は何人か。
Lesson2-2 ニュートレジャー Stage1 3rd Edition 【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中1英語#This is~. That is~. What is~? の文(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage1 3rd Edition Lesson2-2のKeyPoint例文解説です。
この動画を見る
ニュートレジャー Stage1 3rd Edition Lesson2-2のKeyPoint例文解説です。
数と式 根号を含む計算【ホーン・フィールドがていねいに解説】

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\dfrac{\sqrt2}{\sqrt2-1}$の整数部分をa、小数部分をbとする。次の式の値を求めよ。
(1)$a$ (2)$b$ (3)$a+b+b^2$
次の各場合について、$\sqrt{x^2-10x+25}$をxの多項式で表せ。
(1)$x\geqq 5$ (2)$x\lt 5$
この動画を見る
$\dfrac{\sqrt2}{\sqrt2-1}$の整数部分をa、小数部分をbとする。次の式の値を求めよ。
(1)$a$ (2)$b$ (3)$a+b+b^2$
次の各場合について、$\sqrt{x^2-10x+25}$をxの多項式で表せ。
(1)$x\geqq 5$ (2)$x\lt 5$
Lesson2-2 NT Stage1 3rd Edition 【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中1英語#This is~. That is~. What is~? の文(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson2#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage1 Lesson2-2のKeyPoint例文解説です。
疑問詞whatの使い方
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage1 Lesson2-2のKeyPoint例文解説です。
疑問詞whatの使い方
Lesson2-1 NT Stage1 3rd Edition【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中1英語#He(She) is~. Who is~?の文(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson2#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
N.T. ENGLISH SERIES Third Edition Stage1 Lesson2-1のKeyPoint例文解説です。
この動画を見る
N.T. ENGLISH SERIES Third Edition Stage1 Lesson2-1のKeyPoint例文解説です。
Lesson2-1 ニュートレジャー Stage1 3rd Edition【ダスカロイがていねいに解説】

単元:
#英語(中学生)#中1英語#He(She) is~. Who is~?の文(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ニュートレジャー Stage1 3rd Edition Lesson2-1のKeyPoint例文解説です。
この動画を見る
ニュートレジャー Stage1 3rd Edition Lesson2-1のKeyPoint例文解説です。
【情報Ⅰ】コンピュータでの数値の内部表現

【情報Ⅰ】ハードウェアとは?

図形と計量 文字で三角比を表す【NI・SHI・NOがていねいに解説】

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\angle C=90°$ である直角三角形ABCにおいて,$\angle A=\theta, AB=k$ とする。頂点Cから辺ABに下ろした垂線を CD とするとき,次の線分の長さを$k,\theta$を用いて表せ。(1) BC (2) AC (3) AD (4) CD (5) BD
この動画を見る
$\angle C=90°$ である直角三角形ABCにおいて,$\angle A=\theta, AB=k$ とする。頂点Cから辺ABに下ろした垂線を CD とするとき,次の線分の長さを$k,\theta$を用いて表せ。(1) BC (2) AC (3) AD (4) CD (5) BD
図形と計量 建物の高さを求める【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
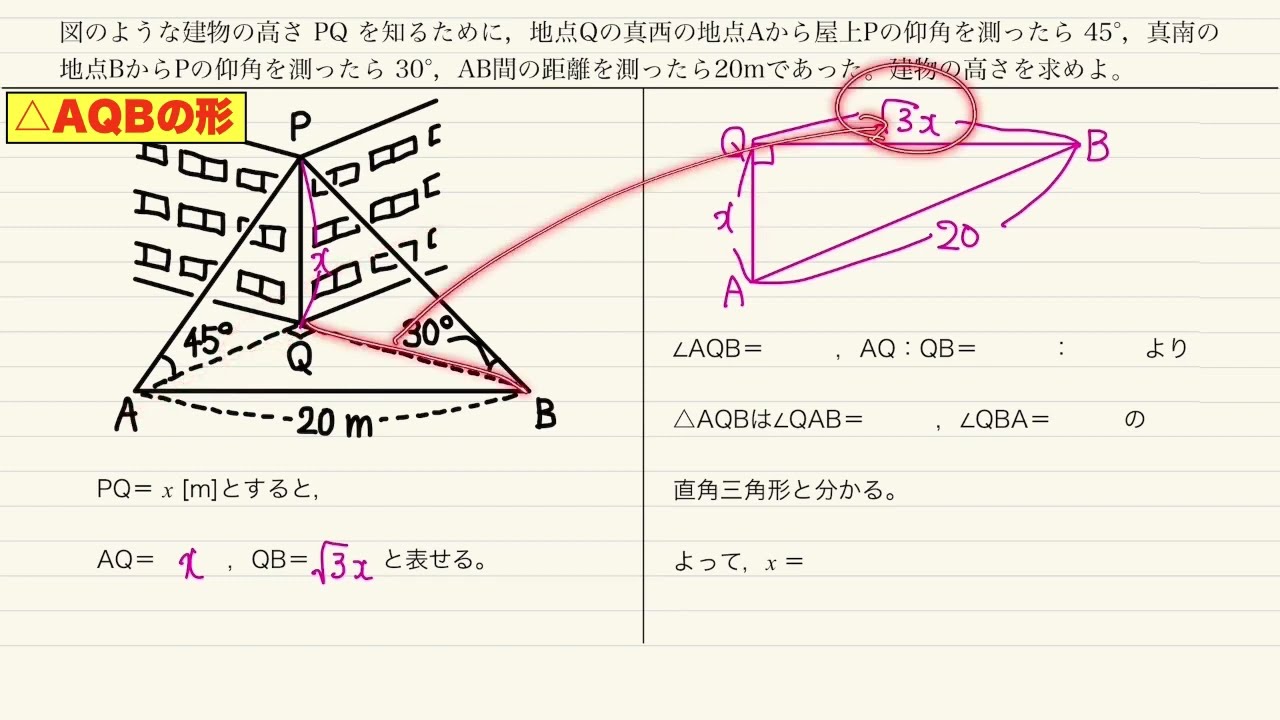
建物の高さ PQ を知るために,地点Qの真西の地点Aから屋上Pの仰角を測ったら 45°,真南の地点BからPの仰角を測ったら 30°,AB間の距離を測ったら20mであった。建物の高さを求めよ。
この動画を見る
建物の高さ PQ を知るために,地点Qの真西の地点Aから屋上Pの仰角を測ったら 45°,真南の地点BからPの仰角を測ったら 30°,AB間の距離を測ったら20mであった。建物の高さを求めよ。
図形と計量 三角比の空間への利用【NI・SHI・NOがていねいに解説】
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
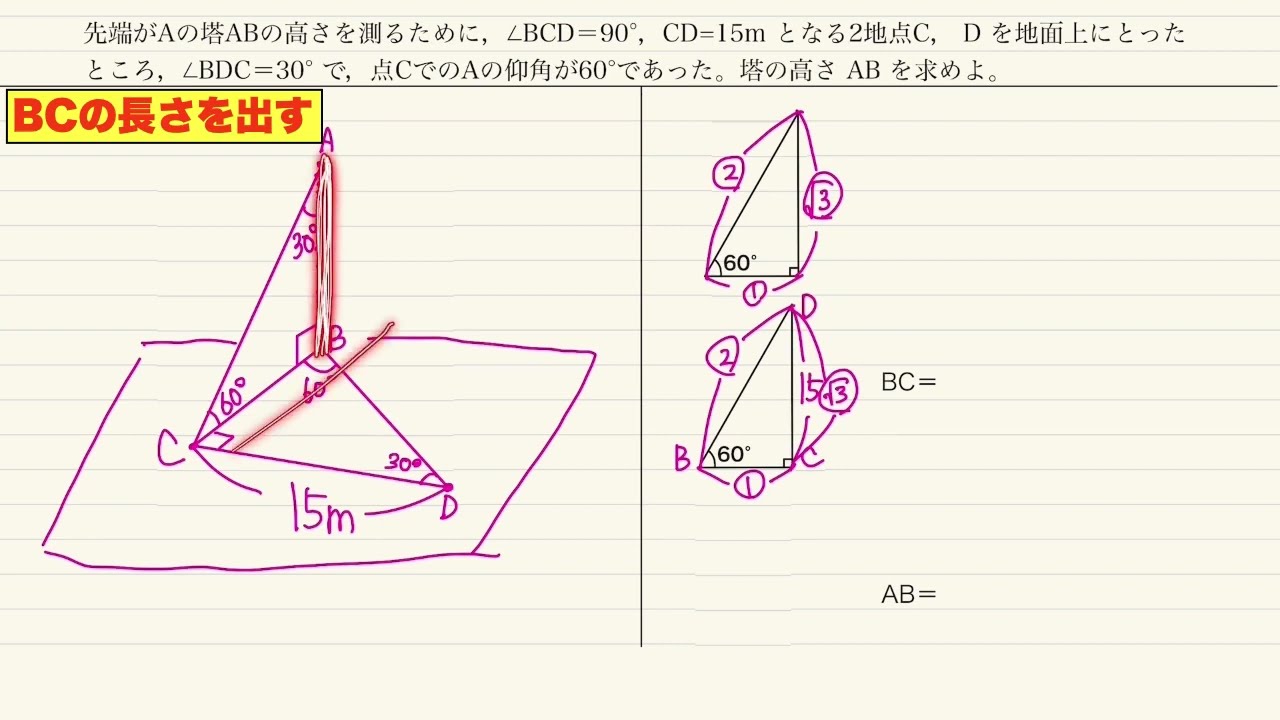
先端がAの塔ABの高さを測るために,$\angle BCD=90°,CD=15m$ となる2地点C, D を地面上にとったところ,$\angle BDC=30°$ で,点CでのAの仰角が$60°$であった。塔の高さ AB を求めよ。
この動画を見る
先端がAの塔ABの高さを測るために,$\angle BCD=90°,CD=15m$ となる2地点C, D を地面上にとったところ,$\angle BDC=30°$ で,点CでのAの仰角が$60°$であった。塔の高さ AB を求めよ。
【受験算数】さいころを3回振ったところ、1回目よりも2回目の方が大きい目が出て、さらに2回目よりも3回目の方が大きい目が出ました。このような目の出方は□通りです。

単元:
#算数(中学受験)#場合の数#場合の数
指導講師:
理数個別チャンネル
問題文全文(内容文):
さいころを3回振ったところ、1回目よりも2回目の方が大きい目が出て、さらに2回目よりも3回目の方が大きい目が出ました。このような目の出方は□通りです。
この動画を見る
さいころを3回振ったところ、1回目よりも2回目の方が大きい目が出て、さらに2回目よりも3回目の方が大きい目が出ました。このような目の出方は□通りです。
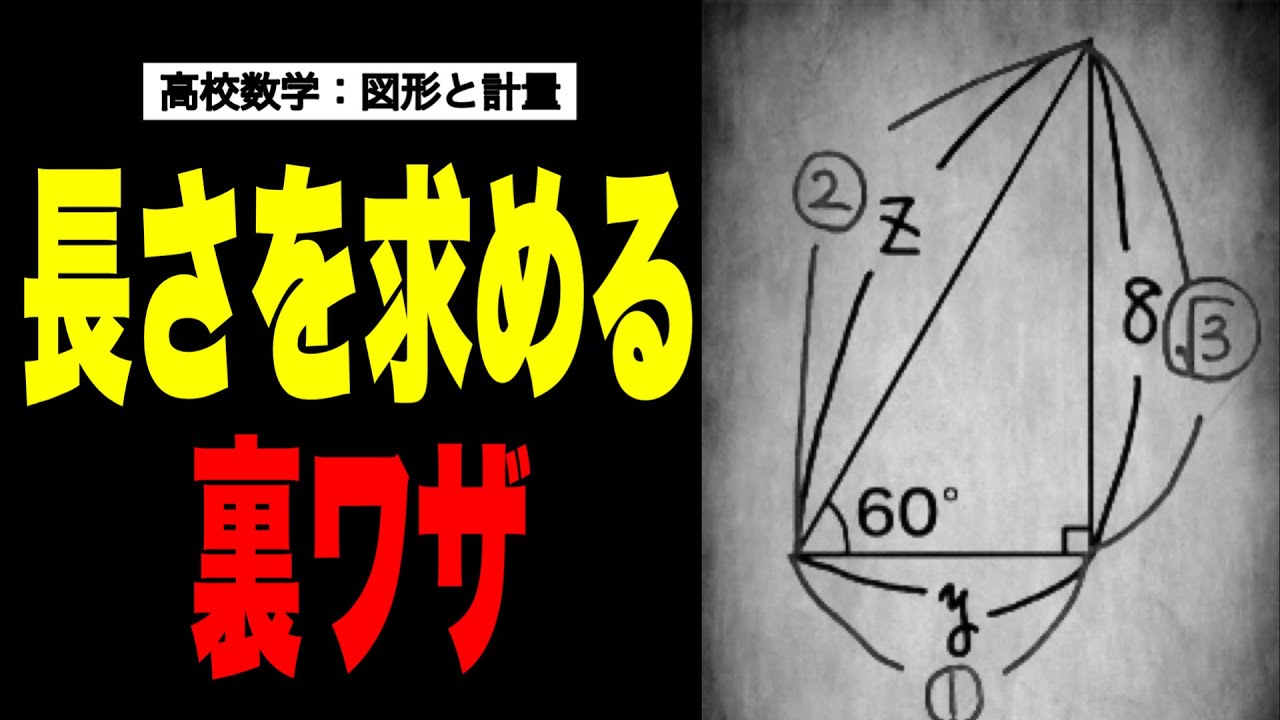
【数Ⅰ】図形と計量:三角比:3辺の比を求める裏ワザ!
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
有名角の三角比を使わずに辺の長さを出す裏ワザ!
この動画を見る
有名角の三角比を使わずに辺の長さを出す裏ワザ!
Lesson6-2 ニュートレジャー Stage1 3rd Edition【しまだじろうがていねいに解説】

単元:
#英語(中学生)#中2英語#can、could、be able to、may、must、have to、should、助動詞を使った表現
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson6-2は助動詞canの使い方と、自動詞と他動詞についてです。助動詞って何?自動詞と他動詞って何?基礎からわかりやすく解説!また、テキストに出て来る単語のチェックや動詞の使い方なども、ていねいに解説しているので基礎から応用までしっかり理解しましょう!
この動画を見る
Lesson6-2は助動詞canの使い方と、自動詞と他動詞についてです。助動詞って何?自動詞と他動詞って何?基礎からわかりやすく解説!また、テキストに出て来る単語のチェックや動詞の使い方なども、ていねいに解説しているので基礎から応用までしっかり理解しましょう!
Lesson6-2 NT Stage1 3rd Edition【しまだじろうがていねいに解説】

単元:
#英語(中学生)#英語(高校生)#英文法#品詞と文型、句と節#中1英語#canの文(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson6#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
Lesson6-2は助動詞canの使い方と、自動詞と他動詞についてです。助動詞って何?自動詞と他動詞って何?基礎からわかりやすく解説!また、テキストに出て来る単語のチェックや動詞の使い方なども、ていねいに解説しているので基礎から応用までしっかり理解しましょう!
この動画を見る
Lesson6-2は助動詞canの使い方と、自動詞と他動詞についてです。助動詞って何?自動詞と他動詞って何?基礎からわかりやすく解説!また、テキストに出て来る単語のチェックや動詞の使い方なども、ていねいに解説しているので基礎から応用までしっかり理解しましょう!
【数B】第1項から第10項までの和が4、第1項から第20項までの和が24である等比数列について、第1項から第40項までの和を求めよ

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1項から第10項までの和が4、第1項から第20項までの和が24である等比数列について、第1項から第40項までの和を求めよ
この動画を見る
第1項から第10項までの和が4、第1項から第20項までの和が24である等比数列について、第1項から第40項までの和を求めよ
場合の数 集合の基本~ベン図を描こう~【さこすけ's サイエンスがていねいに解説】

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$U={1,2,3,4,5,6,7,8,9}$を全体集合とする。Uの部分集合A,Bについて、
$A∩B={2}$,(Aの補集合)$∩B={2,4,6,8}$,(Aの補集合)$∩$(Bの補集合)$={1,9}$であるとき、次の集合を求めよ。
(1)$A∪B$ (2)$B$ (3)$A∩$(Bの補集合)
U={$x\vert 1\leqq x\leqq 10$,xは整数}を全体集合とする。Uの部分集合
$A={1,2,3,4,8},B={3,4,5,6},C={2,3,6,7}$について、次の集合を求めよ。
(1)$A∩B∩C$ (2)$A∪B∪C$ (3)$A∩B∩$(Cの補集合) (4)(Aの補集合)$∩B∩$(Cの補集合) (5)($A∩B∩C$の補集合) (6)$(A∪C)∩$(Bの補集合)
$A={1,3,3a-2},B={-5,a+2,a^2-2a+1},A∩B={1,4}$のとき、
定数aの値と和集合$A∪B$を求めよ
この動画を見る
$U={1,2,3,4,5,6,7,8,9}$を全体集合とする。Uの部分集合A,Bについて、
$A∩B={2}$,(Aの補集合)$∩B={2,4,6,8}$,(Aの補集合)$∩$(Bの補集合)$={1,9}$であるとき、次の集合を求めよ。
(1)$A∪B$ (2)$B$ (3)$A∩$(Bの補集合)
U={$x\vert 1\leqq x\leqq 10$,xは整数}を全体集合とする。Uの部分集合
$A={1,2,3,4,8},B={3,4,5,6},C={2,3,6,7}$について、次の集合を求めよ。
(1)$A∩B∩C$ (2)$A∪B∪C$ (3)$A∩B∩$(Cの補集合) (4)(Aの補集合)$∩B∩$(Cの補集合) (5)($A∩B∩C$の補集合) (6)$(A∪C)∩$(Bの補集合)
$A={1,3,3a-2},B={-5,a+2,a^2-2a+1},A∩B={1,4}$のとき、
定数aの値と和集合$A∪B$を求めよ
Lesson6-1 ニュートレジャー Stage1 3rd Edition【まどか's Englishがていねいに解説】

Lesson6-1 NT Stage1 3rd Edition【まどか's Englishがていねいに解説】
単元:
#英語(中学生)#英語(高校生)#会話文・イディオム・構文・英単語#中1英語#中2英語#会話文#命令文、否定の命令文、ていねいな命令文、Let's~.の文、あいさつ#命令文、Let's~、Don't~、命令文, and(or)~の文
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson6#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
6-1文法解説です
この動画を見る
6-1文法解説です
図形と計量 円に内接する四角形の面積【烈's study!がていねいに解説】
単元:
#数Ⅰ#数A#図形の性質#図形と計量#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
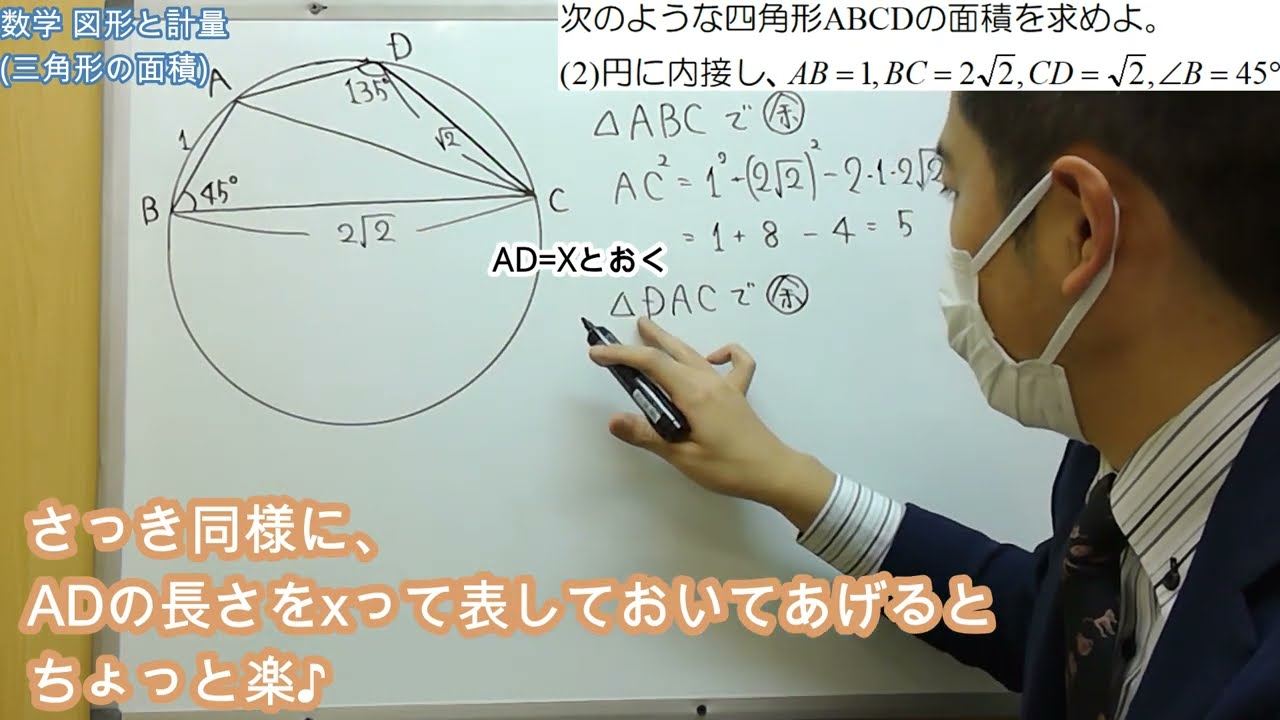
次のような四角形ABCDの面積を求めよ。
(1)円に内接し、$AB=4、BC=3、CD=1、\angle B=60°$
(2)円に内接し、$AB=1、BC=2\sqrt2、CD=\sqrt2、\angle B=45°$
この動画を見る
次のような四角形ABCDの面積を求めよ。
(1)円に内接し、$AB=4、BC=3、CD=1、\angle B=60°$
(2)円に内接し、$AB=1、BC=2\sqrt2、CD=\sqrt2、\angle B=45°$
図形と計量 四角形の面積【烈's study!がていねいに解説】

単元:
#数Ⅰ#数A#図形の性質#図形と計量#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のような四角形ABCDの面積を求めよ。
(1)$\angle A=135°,\angle C=45°,AB=1,BC=3,CD=\sqrt2,DA=\sqrt2$
(2)$\angle B=120°,AB=3,BC=5,CD=5,DA=4$
この動画を見る
次のような四角形ABCDの面積を求めよ。
(1)$\angle A=135°,\angle C=45°,AB=1,BC=3,CD=\sqrt2,DA=\sqrt2$
(2)$\angle B=120°,AB=3,BC=5,CD=5,DA=4$
【数A】【難問】正二十面体の体積を求めよ。

単元:
#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)
教材:
#チャート式#青チャートⅠ・A#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1辺の長さが1の正二十面体の体積を求めなさい。
この動画を見る
1辺の長さが1の正二十面体の体積を求めなさい。
図形と計量 三角形の面積 二等分線の利用【烈's study!がていねいに解説】
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
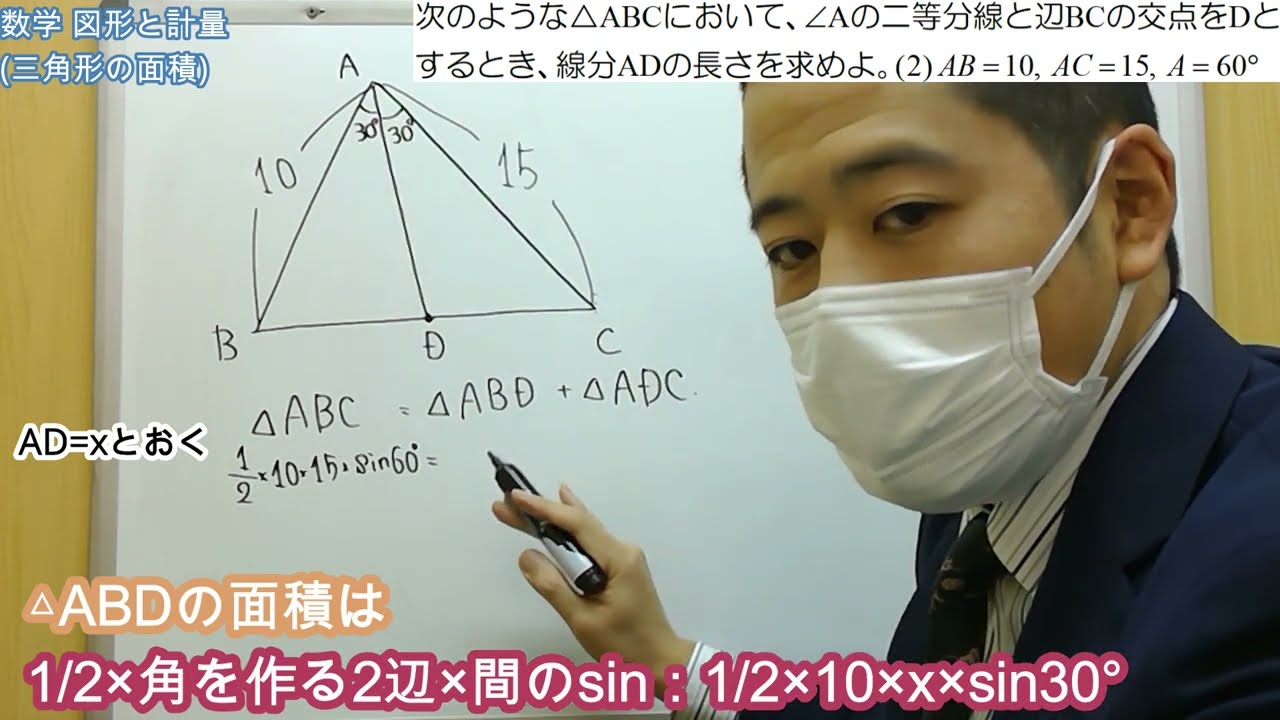
次のような$△ABC$について、$\angle A$の二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)$AB=4、AC=3、A=120°$
(2)$AB=10、AC=15、A=60°$
この動画を見る
次のような$△ABC$について、$\angle A$の二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)$AB=4、AC=3、A=120°$
(2)$AB=10、AC=15、A=60°$
図形と計量 平行四辺形の面積を求める【烈's study!がていねいに解説】

単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のような平行四辺形ABCDの面積を求めよ。
(1)$AB=3、BC=5、\angle ABC=60°$
(2)$AB=4、AD=6、\angle ABC=135°$
この動画を見る
次のような平行四辺形ABCDの面積を求めよ。
(1)$AB=3、BC=5、\angle ABC=60°$
(2)$AB=4、AD=6、\angle ABC=135°$
【英語】共通テストの落穂拾い4第6問 倒置など

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#構文#大学入試過去問(英語)#共通テスト
指導講師:
理数個別チャンネル
問題文全文(内容文):
ついついスルーしがちな共通テストの本文よりおいしい構文やフレーズなどを拾っていきます。第6問では倒置などについて。
この動画を見る
ついついスルーしがちな共通テストの本文よりおいしい構文やフレーズなどを拾っていきます。第6問では倒置などについて。
【英語】共通テストの落穂拾い3第4~5問 文頭のrather thanなど

単元:
#英語(高校生)#会話文・イディオム・構文・英単語#構文#大学入試過去問(英語)#共通テスト
指導講師:
理数個別チャンネル
問題文全文(内容文):
ついついスルーしがちな共通テストの本文よりおいしい構文やフレーズなどを拾っていきます。第4~5問。去年も共通テストに出現したあの単語なども紹介します。
この動画を見る
ついついスルーしがちな共通テストの本文よりおいしい構文やフレーズなどを拾っていきます。第4~5問。去年も共通テストに出現したあの単語なども紹介します。




