 理数個別チャンネル
理数個別チャンネル
 理数個別チャンネル
理数個別チャンネル
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【英語】I want to become a singer としない理由!『変化』の動詞すべておさらい

単元:
#英語(中学生)#英語(高校生)#英文法#品詞と文型、句と節#中2英語#形容詞・副詞#文型(第1文型、第2文型、第3文型、第4文型、第5文型)
指導講師:
理数個別チャンネル
問題文全文(内容文):
意外と軽視されがちな、補語を取る動詞たち!その中でも
『状態の変化』を表す動詞は意外といろいろあります!
一緒にすべておさらいします
この動画を見る
意外と軽視されがちな、補語を取る動詞たち!その中でも
『状態の変化』を表す動詞は意外といろいろあります!
一緒にすべておさらいします
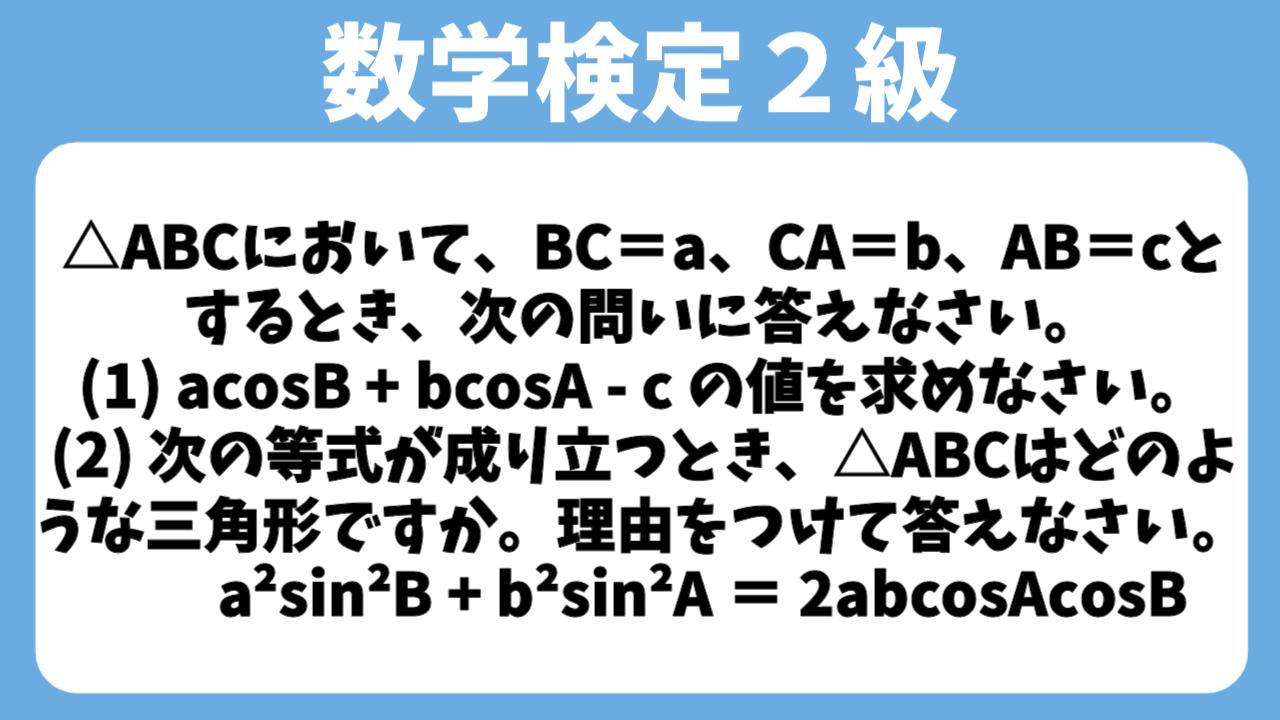
【数検2級】数学検定2級2次:問題6
単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学検定#数学検定2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題6.(必須)
△ABCにおいて、$BC=a、CA=b、AB=c$とするとき、次の問いに答えなさい。
(1)$a\cos B+b\cos A-c$ の値を求めなさい。この問題は解法の過程を記述せずに、答えだけを書いてください。
(2) 次の等式が成り立つとき、△ABCはどのような三角形ですか。理由をつけて答えなさい。
$a^2\sin^2B+b^2\sin^2 A=2ab\cos A\cos B$
この動画を見る
問題6.(必須)
△ABCにおいて、$BC=a、CA=b、AB=c$とするとき、次の問いに答えなさい。
(1)$a\cos B+b\cos A-c$ の値を求めなさい。この問題は解法の過程を記述せずに、答えだけを書いてください。
(2) 次の等式が成り立つとき、△ABCはどのような三角形ですか。理由をつけて答えなさい。
$a^2\sin^2B+b^2\sin^2 A=2ab\cos A\cos B$
【英語】授与動詞の受動態 そして I was bought の謎

【数学】高校入試:2022年度神奈川県立高校入試数学大問3ア(ⅱ)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
(ア) 右の図1のように,AB<AC,∠ABCが鋭角の平行四辺形ABCDがあり,∠BCDの二等分線と辺ADとの交点をEとする。
また,辺BCの延長上に点Fを,CF=DFとなるようにとる。
さらに,辺CD上に点Gを,CG>GDとなるようにとり,線分DF上に点Hを,DG=DHとなるようにとる。
このとき,四角形CFDEが平行四辺形になるときの,∠ABCの大きさとして正しいものを次の1~4の中から1つ選び,その番号を答えなさい。
1.45° 2.50° 3.55° 4.60°
この動画を見る
(ア) 右の図1のように,AB<AC,∠ABCが鋭角の平行四辺形ABCDがあり,∠BCDの二等分線と辺ADとの交点をEとする。
また,辺BCの延長上に点Fを,CF=DFとなるようにとる。
さらに,辺CD上に点Gを,CG>GDとなるようにとり,線分DF上に点Hを,DG=DHとなるようにとる。
このとき,四角形CFDEが平行四辺形になるときの,∠ABCの大きさとして正しいものを次の1~4の中から1つ選び,その番号を答えなさい。
1.45° 2.50° 3.55° 4.60°
【英語】each otherは主語にできない!代替語も紹介するよ~

単元:
#英語(高校生)#英文法#名詞・冠詞・代名詞
指導講師:
理数個別チャンネル
問題文全文(内容文):
意外と知らない!?each otherの使い方を紹介します!(実は所有格もあるよ)
この動画を見る
意外と知らない!?each otherの使い方を紹介します!(実は所有格もあるよ)
【中学受験理科】地層と岩石②『示相化石:俳句で覚える示相化石!』

【中学受験理科】地層と岩石:②『示相化石:俳句で覚える示相化石!』

【英語】過去完了の使い方について解説します

単元:
#英語(高校生)#英文法#時制
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の中で英文が正しいのはどれ?
I had made a car.
I have a car that I have made in London.
I had a car that I had made in London.
I have a car that I had made in London.
この動画を見る
次の中で英文が正しいのはどれ?
I had made a car.
I have a car that I have made in London.
I had a car that I had made in London.
I have a car that I had made in London.
2020年度第4回K塾記述高2模試全問解説 #shorts #K塾模試 #りすうこべつチャンネル

【数学】高校入試:2022年度神奈川県立高校入試数学大問3ア(ⅰ)

単元:
#数学(中学生)#高校入試過去問(数学)#神奈川県公立高校入試
指導講師:
理数個別チャンネル
問題文全文(内容文):
(ア) 右の図1のように,AB<AC,∠ABCが鋭角の平行四辺形ABCDがあり,∠BCDの二等分線と辺ADとの交点をEとする。
また,辺BCの延長上に点Fを,CF=DFとなるようにとる。
さらに,辺CD上に点Gを,CG>GDとなるようにとり,線分DF上に点Hを,DG=DHとなるようにとる。
このとき,三角形DEGと三角形DCHが合同であることを証明しなさい。
この動画を見る
(ア) 右の図1のように,AB<AC,∠ABCが鋭角の平行四辺形ABCDがあり,∠BCDの二等分線と辺ADとの交点をEとする。
また,辺BCの延長上に点Fを,CF=DFとなるようにとる。
さらに,辺CD上に点Gを,CG>GDとなるようにとり,線分DF上に点Hを,DG=DHとなるようにとる。
このとき,三角形DEGと三角形DCHが合同であることを証明しなさい。
【中学受験理科】地層と岩石①『示準化石:語呂合わせと写真と絵で覚えよう!』

【受験理科】地層と岩石:①『示準化石:語呂合わせと写真と絵で覚えよう!』

【世界史】古代ローマ:ホルテンシウス法まで

【公民】国会の語呂合わせ

単元:
#理科(中学受験)#社会(中学受験)#社会(中学生)#公民#公民
指導講師:
理数個別チャンネル
問題文全文(内容文):
国会のしごとについて、定番(?)の語呂合わせで紹介します!
この動画を見る
国会のしごとについて、定番(?)の語呂合わせで紹介します!
Lesson1 問題演習 NT Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中1英語#I am~. You are~.の文(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson1#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
■(1)~(3)を英語にしなさい。
(1)私の名前はタロウです。(2)「あなたはフランス出身ですか」「はい、そうです。」(3)私は中国出身ではありません。
■(4)(5)の英文の誤りを訂正しなさい。
(4)私は日本出身です。 I’m not from japan.(5)「あなたはユミですか」「いいえ、違います。」Are You yumi. No you are not.
この動画を見る
■(1)~(3)を英語にしなさい。
(1)私の名前はタロウです。(2)「あなたはフランス出身ですか」「はい、そうです。」(3)私は中国出身ではありません。
■(4)(5)の英文の誤りを訂正しなさい。
(4)私は日本出身です。 I’m not from japan.(5)「あなたはユミですか」「いいえ、違います。」Are You yumi. No you are not.
【英語】Lesson1 問題演習 Stage1【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中1英語
指導講師:
理数個別チャンネル
問題文全文(内容文):
■(1)~(3)を英語にしなさい。
(1)私の名前はタロウです。(2)「あなたはフランス出身ですか」「はい、そうです。」(3)私は中国出身ではありません。
■(4)(5)の英文の誤りを訂正しなさい。
(4)私は日本出身です。 I’m not from japan.(5)「あなたはユミですか」「いいえ、違います。」Are You yumi. No you are not.
この動画を見る
■(1)~(3)を英語にしなさい。
(1)私の名前はタロウです。(2)「あなたはフランス出身ですか」「はい、そうです。」(3)私は中国出身ではありません。
■(4)(5)の英文の誤りを訂正しなさい。
(4)私は日本出身です。 I’m not from japan.(5)「あなたはユミですか」「いいえ、違います。」Are You yumi. No you are not.
【英語】え!固有名詞にtheをつけるの!?

【受験算数】流水算・通過算:(練習❺)通過算 途中で速さが変わる【予習シリーズ演習問題集・小5下】

単元:
#算数(中学受験)#速さ#旅人算・通過算・流水算
教材:
#予習シ#予習シ演問・小5下#中学受験教材#流水算、通過算
指導講師:
理数個別チャンネル
問題文全文(内容文):
長さ180mで秒速24mで走っている電車Aが、長さが120mの電車Bに追いついてから追いこすまでに1分15秒かかりました。これについて、次の問いに答えなさい。
(1)電車Bの速さは秒速何mですか。
(2)電車Bは電車Aに追いこされてから1分後に、秒速34mにして電車Aを追いかけました。電車Bが電車Aを追いぬくのは、秒速34mにしてから何秒後ですか。
この動画を見る
長さ180mで秒速24mで走っている電車Aが、長さが120mの電車Bに追いついてから追いこすまでに1分15秒かかりました。これについて、次の問いに答えなさい。
(1)電車Bの速さは秒速何mですか。
(2)電車Bは電車Aに追いこされてから1分後に、秒速34mにして電車Aを追いかけました。電車Bが電車Aを追いぬくのは、秒速34mにしてから何秒後ですか。
【英語】え!waterってsつけていいの!?

単元:
#英語(高校生)#英文法#会話文・イディオム・構文・英単語#名詞・冠詞・代名詞#会話文
指導講師:
理数個別チャンネル
問題文全文(内容文):
『数えられない名詞は、複数形にしない!』
というのは常識ですが
watersとかrainsというのが実はある!?
不思議な名詞をご紹介します。
この動画を見る
『数えられない名詞は、複数形にしない!』
というのは常識ですが
watersとかrainsというのが実はある!?
不思議な名詞をご紹介します。
【数B】ベクトル:ベクトルの基本⑮直線の方程式を求める

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
A(3,5),方向ベクトルd=(1,2)のとき直線の方程式を求めよ。
A(1,3),B(2,4)のとき2点を通る直線の方程式を求めよ。
A(3,2),法線ベクトルd=(4,5)のとき直線の方程式を求めよ。
この動画を見る
A(3,5),方向ベクトルd=(1,2)のとき直線の方程式を求めよ。
A(1,3),B(2,4)のとき2点を通る直線の方程式を求めよ。
A(3,2),法線ベクトルd=(4,5)のとき直線の方程式を求めよ。
【数C】ベクトルの基本⑮直線の方程式を求める

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
A(3,5),方向ベクトルd=(1,2)のとき直線の方程式を求めよ。
A(1,3),B(2,4)のとき2点を通る直線の方程式を求めよ。
A(3,2),法線ベクトルd=(4,5)のとき直線の方程式を求めよ。
この動画を見る
A(3,5),方向ベクトルd=(1,2)のとき直線の方程式を求めよ。
A(1,3),B(2,4)のとき2点を通る直線の方程式を求めよ。
A(3,2),法線ベクトルd=(4,5)のとき直線の方程式を求めよ。
【数B】ベクトル:一次独立なベクトルで他のベクトルを扱おう!

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
アドバンスプラス数学B
問題618
$\vec{a}=(2,5),\vec{b}=(1,3)$がある。次のベクトルを$\vec{a}+m \vec{b}$の形で表せ。
(1)$\vec{c}=(1,0)$
この動画を見る
アドバンスプラス数学B
問題618
$\vec{a}=(2,5),\vec{b}=(1,3)$がある。次のベクトルを$\vec{a}+m \vec{b}$の形で表せ。
(1)$\vec{c}=(1,0)$
【数C】一次独立なベクトルで他のベクトルを扱おう!

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#アドバンスプラス#アドバンスプラス数Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
アドバンスプラス数学B
問題618
vec(a)=(2,5),vec(b)=(1,3)がある。次のベクトルをl vec(a)+m vec(b)の形で表せ。
(1) vec(c)=(1,0)
この動画を見る
アドバンスプラス数学B
問題618
vec(a)=(2,5),vec(b)=(1,3)がある。次のベクトルをl vec(a)+m vec(b)の形で表せ。
(1) vec(c)=(1,0)
【英語】Lesson1-1 ②③ Stage1 【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#中1英語#I am~. You are~.の文(肯定文・否定文・疑問文)
指導講師:
理数個別チャンネル
問題文全文(内容文):
be動詞 am areの否定文、疑問文の作り方に関して解説していきます.
この動画を見る
be動詞 am areの否定文、疑問文の作り方に関して解説していきます.
Lesson1-1 ②③ NT Stage1 3rd Edition【岡ちゃん先生がていねいに解説】

単元:
#英語(中学生)#I am~. You are~.の文(肯定文・否定文・疑問文)
教材:
#NT ENGLISH SERIES#Third Edition Stage1#Lesson1#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
be動詞 am areの否定文、疑問文の作り方
この動画を見る
be動詞 am areの否定文、疑問文の作り方
【英語】長い一文を読み解く5つのポイント!難関国公立大入試対策

単元:
#英語(高校生)#英文法#英文解釈#文の種類#関係代名詞・関係副詞・複合関係詞#接続詞
指導講師:
理数個別チャンネル
問題文全文(内容文):
めちゃくちゃ長い1文をどのように読んでいくか説明しています!
文はこちら
"Does your country have four seasons?"
It is a question that can perplex and amuse many foreigners as it is often asked with what seems to be a sincere belief that Japan is the only country in the world that has four seasons.
この動画を見る
めちゃくちゃ長い1文をどのように読んでいくか説明しています!
文はこちら
"Does your country have four seasons?"
It is a question that can perplex and amuse many foreigners as it is often asked with what seems to be a sincere belief that Japan is the only country in the world that has four seasons.
【数B】ベクトル:ベクトルの基本⑭係数比較、メネラウスの定理でベクトルを求める

単元:
#数A#図形の性質#平面上のベクトル#内心・外心・重心とチェバ・メネラウス#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD,BEの交点をPとする。ABをb,ACをcとするとき、APをb,cを用いて表せ.
この動画を見る
三角形ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD,BEの交点をPとする。ABをb,ACをcとするとき、APをb,cを用いて表せ.
【数C】ベクトルの基本⑭係数比較、メネラウスの定理でベクトルを求める

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD,BEの交点をPとする。ABをb,ACをcとするとき、APをb,cを用いて表せ
この動画を見る
三角形ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD,BEの交点をPとする。ABをb,ACをcとするとき、APをb,cを用いて表せ
【数B】ベクトル:ベクトルの大きさを自由自在に扱おう!

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
アドバンスプラス数学B
問題617
$\vec{a}=(2,-1)$について、
(1)$\vec{a}$と平行な単位ベクトルを求めよ。
(2)$\vec{a}$と同じ向きで、大きさが5である$\vec{b}$を求めよ。
この動画を見る
アドバンスプラス数学B
問題617
$\vec{a}=(2,-1)$について、
(1)$\vec{a}$と平行な単位ベクトルを求めよ。
(2)$\vec{a}$と同じ向きで、大きさが5である$\vec{b}$を求めよ。
【数C】ベクトルの大きさを自由自在に扱おう!

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#アドバンスプラス#アドバンスプラス数Ⅱ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
アドバンスプラス数学B
問題617
vec(a)=(2,-1)について、
(1) vec(a)と平行な単位ベクトルを求めよ。
(2) vec(a)と同じ向きで、大きさが5であるvec(b)を求めよ。
この動画を見る
アドバンスプラス数学B
問題617
vec(a)=(2,-1)について、
(1) vec(a)と平行な単位ベクトルを求めよ。
(2) vec(a)と同じ向きで、大きさが5であるvec(b)を求めよ。




